Guia de intervenção
Plano de Aula
Plano de aula: Notações fracionárias e decimais de medidas
Plano 3 de uma sequência de 5 planos. Veja todos os planos sobre Relação entre as unidades de medida de massa, capacidade e comprimento
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alexandre Tolentino de Carvalho
Mentor: Fábio Menezes da Silva.
Especialista de área: Fernando Barnabé
Habilidade da BNCC
EF05MA19 - Resolver e elaborar problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais.
Objetivos específicos
- Representar unidades de medidas utilizando notação fracionária e notação decimal.
- Relacionar a transformação de medidas por meio do algoritmo usual ou por meio de divisões sucessivas por 10 relacionando-a com o deslocamento da vírgula.
- Solucionar problemas por meio de investigação de padrões.
Conceito-chave
Notação fracionária e decimal de medidas.
Recursos necessários
- Lápis,
- Borracha,
- Caderno,
- Régua,
- Q.V.L.
Habilidades BNCC:
Objetivos de aprendizagem
- Representar unidades de medidas utilizando notação fracionária e notação decimal.
- Relacionar a transformação de medidas por meio do algoritmo usual ou por meio de divisões sucessivas por 10 relacionando-a com o deslocamento da vírgula.
- Solucionar problemas por meio de investigação de padrões.
Resumo da aula
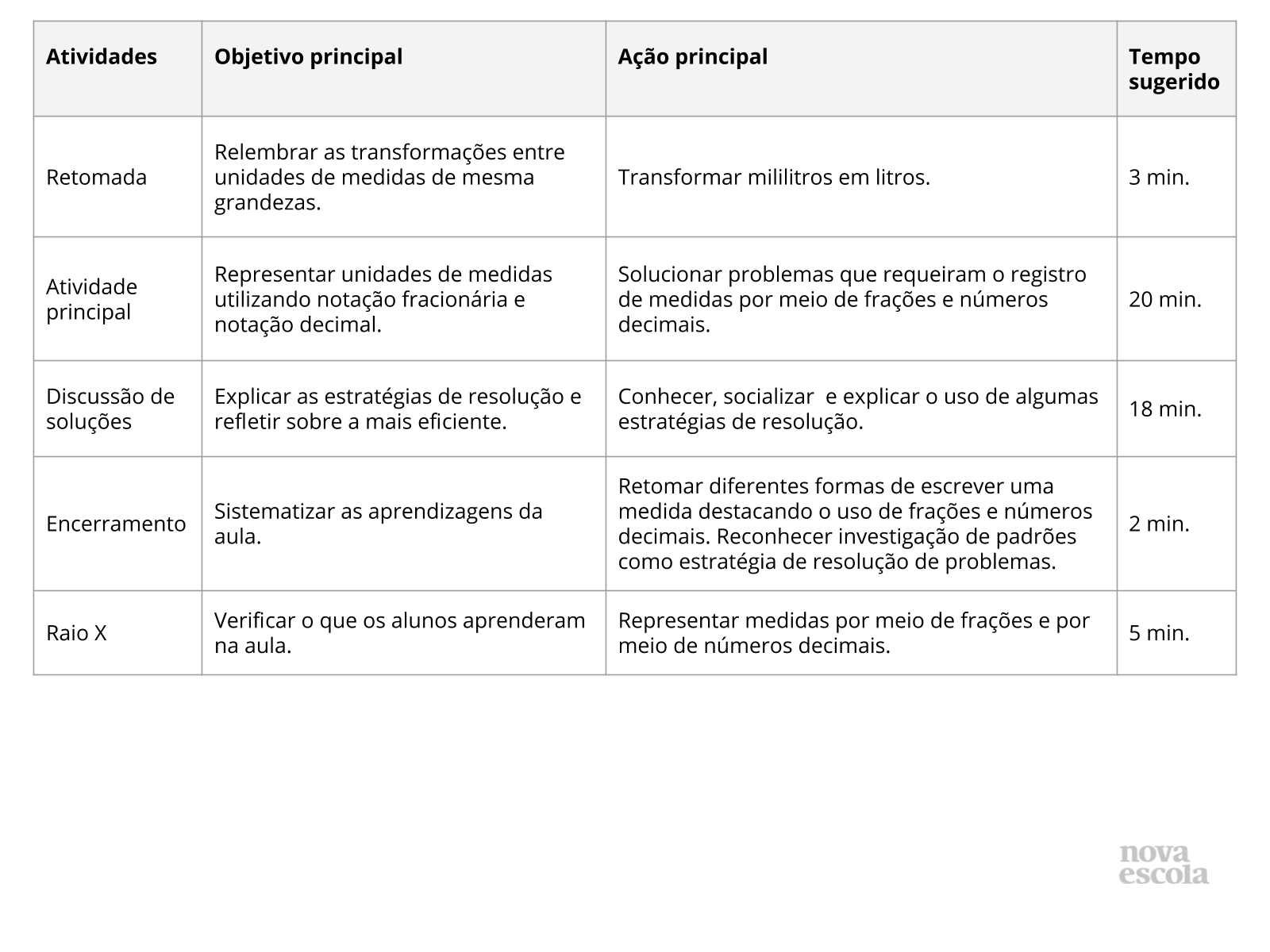 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 3 minutos.
Orientação: Os alunos irão relembrar maneiras de transformar medidas. É importante que compartilhem diferentes maneiras de realizar uma mesma transformação.
Propósito: Relembrar estratégias de transformação de medidas necessárias para os propósitos dessa aula.
Discuta com a turma:
- Em que situações temos que transformar medidas? Por que essas transformações têm que ser feitas?
- Que estratégias de transformação de medidas vocês conhecem?
Atividade principal

Tempo sugerido: 20 minutos.
Orientação: Peça aos alunos para sinalizar as informações mais importantes que os ajudarão a pensar sobre as respostas para as questões do próximo slide. Eles podem anotar essas informações, podem circular, sublinhar ou pintar de cores variadas. Antes de iniciar a solução das questões, eles podem mostrar os dados sinalizados uns para os outros, discutindo sobre a importância de cada informação e o que ela significa e sobre a necessidade de sinalizar algum dado importante que não foi considerado.
Propósito: Apresentar um problema possível de ocorrer na vida real envolvendo representação fracionária e decimal de medidas que leve os alunos a mobilizar conhecimentos necessários para criar estratégias e ferramentas matemáticas úteis para encontrar solução para as questões apontadas.
Discuta com a turma:
- O que entenderam da situação apresentada? Vocês sabem o que é uma instituição de caridade? Conhecem alguma?
- Que informações vocês consideram importantes para a compreensão da situação apresentada? O que significa cada uma dessas informações?
Materiais complementares
Atividade principal

Tempo sugerido: 20 minutos.
Orientação: A reflexão sobre essas questões levará o aluno a perceber que existem outras formas de registrar as medidas, enfatizando a notação fracionária e decimal. Pergunte aos alunos se, assim como aconteceu com Dona Sônia, algum deles ficou em dúvida sobre a proposta do açougueiro.
Propósito: Apresentar um problema possível de ocorrer na vida real envolvendo representação fracionária e decimal de medidas que leve os alunos a mobilizar conhecimentos necessários para criar estratégias e ferramentas matemáticas úteis para encontrar solução para as questões apontadas.
Discuta com a turma:
- Existem outras formas de escrever informações trazidas nessa situação, como o quilograma, 100 gramas, 23 quilogramas?
- Você sabe o que é uma fração? E um número decimal?
- Você seria capaz de escrever 100 gramas utilizando uma fração? E utilizando um número decimal?
Atividade principal

Tempo sugerido: 20 minutos.
Orientação: A questão 3 destacará a presença de variáveis dependentes e independentes. O objetivo é levá-los a perceber que, em uma situação, algumas variáveis dependerão de outras. Assim, no exemplo, a variável quantidade de carne doada dependerá da variável quantidade de carne vendida. A questão 4 levará os alunos ao campo conceitual da proporção. Desse modo, ao perceber, na questão 3, que a quantidade de carne doada dependerá da quantidade de carne vendida, os alunos poderão pensar, na questão 4, que um aumento ou diminuição na variável independente (quantidade vendida) provoca um aumento ou diminuição proporcional na variável dependente (quantidade doada). Na questão 4 se explicita a importância de levar os alunos à investigação de padrões. Esse é um dos princípios para que os alunos, por meio da percepção de padrões, possam compreender a mecânica de procedimentos matemáticos, criar procedimentos próprios utilizando-os como ferramentas para a resolução de problemas e desenvolvimento de conhecimentos matemáticos.
Propósito: Apresentar um problema possível de ocorrer na vida real envolvendo representação fracionária e decimal de medidas que leve os alunos a mobilizar conhecimentos necessários para criar estratégias e ferramentas matemáticas úteis para encontrar solução para as questões apontadas.
Discussão das soluções

Tempo sugerido: 18 minutos.
Orientações: Permita que os alunos compartilhem soluções com os demais colegas de turma. Peça para identificarem semelhanças e as diferentes formas de solucionar a questão. Em seguida, passe para este slide. Nele, os alunos poderão socializar suas respostas e estratégias. Ofereça oportunidades para que os alunos possam participar, realizando conexões com problemas do cotidiano. Primeiramente, permita que os alunos analisem as informações que julgaram ser importantes para solucionar as questões. Leve-os a contrastar suas anotações com essas apresentadas no slide.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discussão das soluções
Tempo sugerido: 18 minutos.
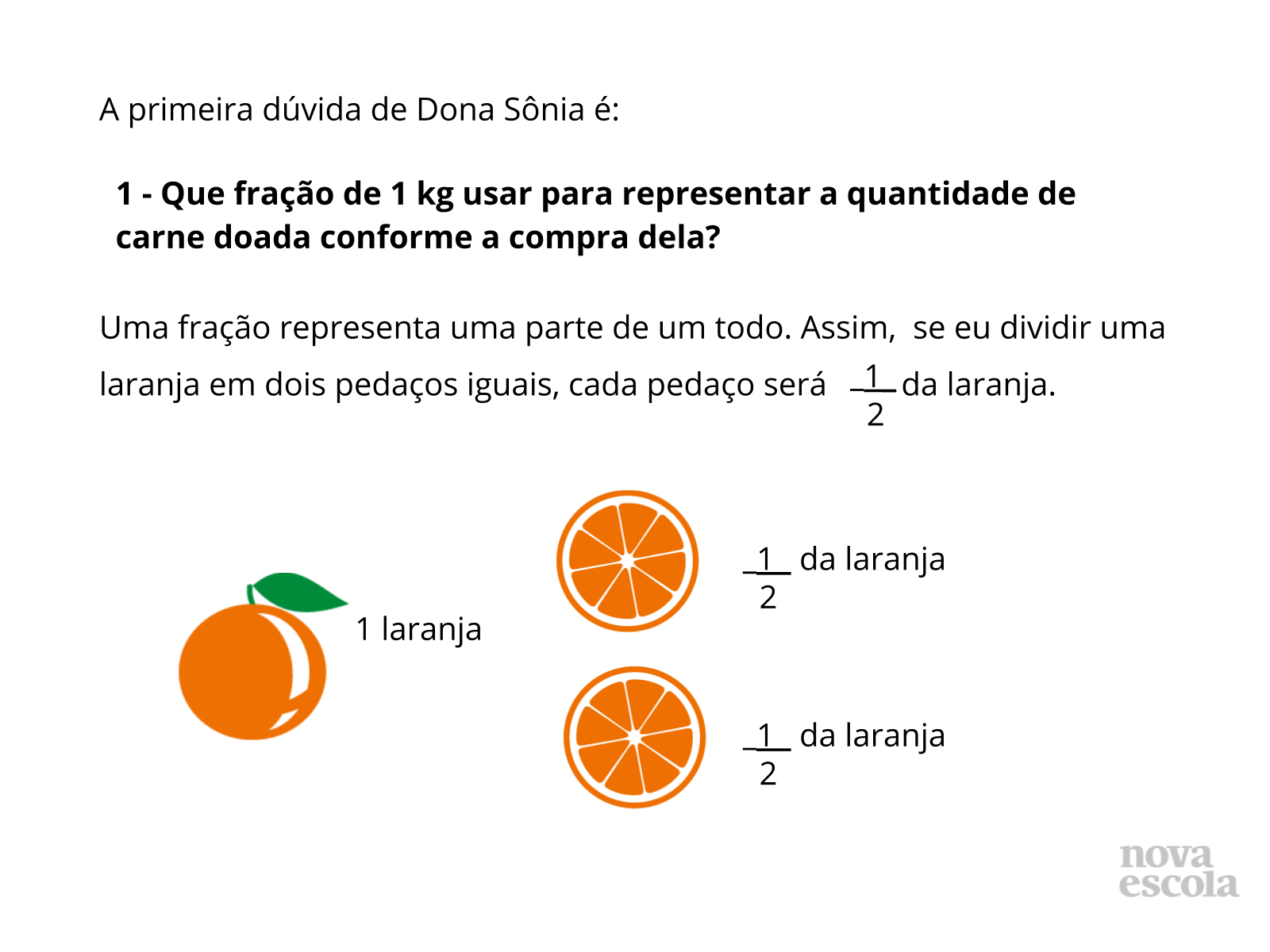
Orientações: Relembre os alunos sobre o significado das notações fracionárias para que possam pensar sobre como utilizar as informações apresentadas na situação para registrar a quantidade pedida por meio de frações.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discuta com a turma:
- Você lembra o que é uma fração? O que seria 1/2 de uma laranja?
Discussão das soluções

Tempo sugerido: 18 minutos.
Orientações: Esse tipo de atividade mostra-se mais complexo do que atividades em que os alunos precisam apenas realizar determinada operação matemática para encontrar uma solução. Ao pensar em formas de registrar determinadas informações textuais por meio de notações matemáticas, o aluno precisa mobilizar várias habilidades como seleção de informações, estudo e tratamento desses dados (em nosso caso, as informações precisam ser convertidas para uma mesma unidade de medida), percepção da função de cada informação matemática na composição da notação (na atividade é necessário saber quem ocupará o numerador e quem ocupará o denominador).
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discuta com a turma:
- Que informações da situação precisam ser selecionadas para serem utilizadas na resolução?
- O que representa cada uma das partes de uma fração? Qual a função de cada uma delas?
Discussão das soluções
Tempo sugerido: 18 minutos.
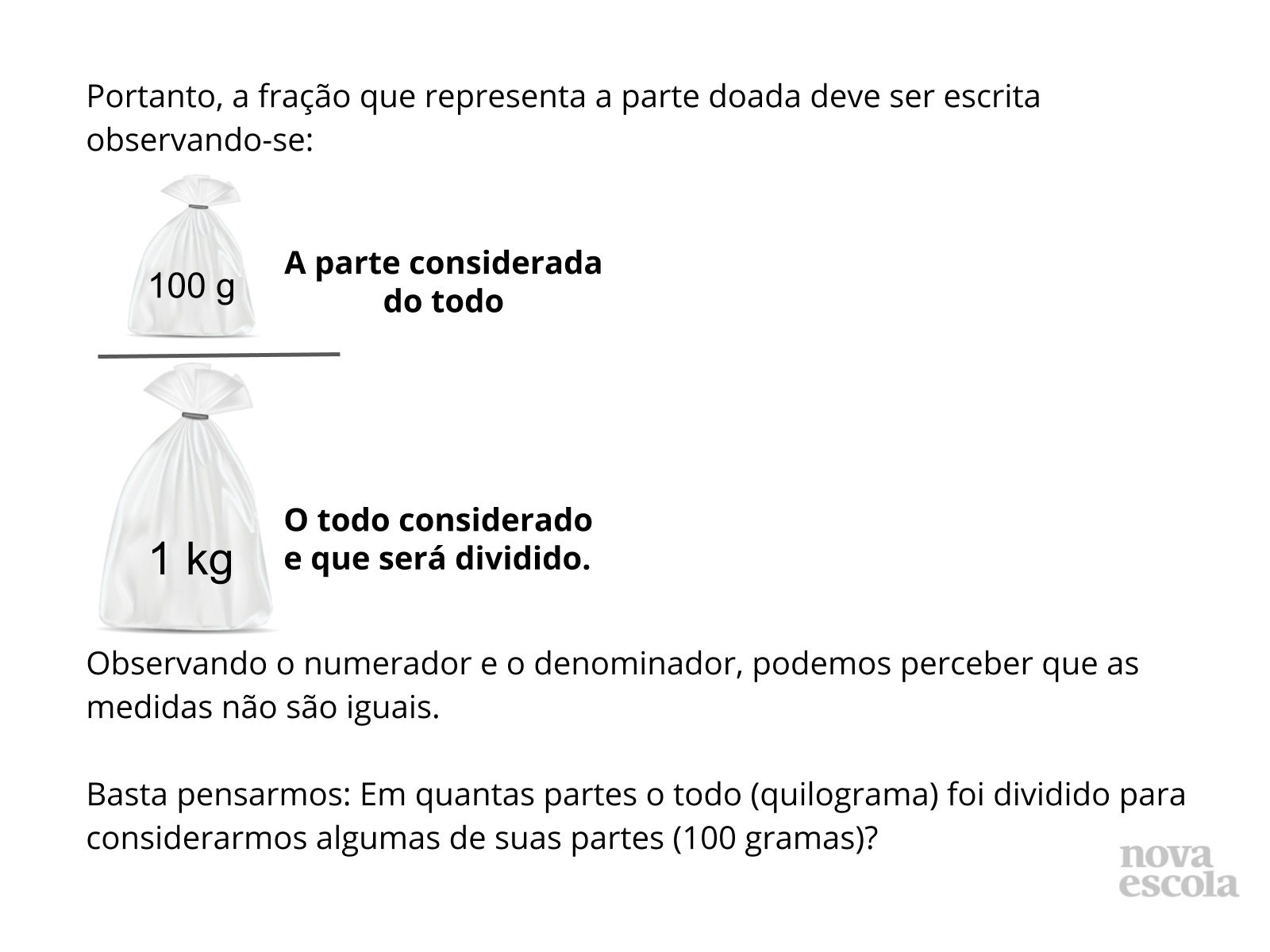
Orientações: Esse tipo de atividade mostra-se mais complexo do que atividades em que os alunos precisam apenas realizar determinada operação matemática para encontrar uma solução. Ao pensar em formas de registrar determinadas informações textuais por meio de notações matemáticas, o aluno precisa mobilizar várias habilidades como seleção de informações, estudo e tratamento desses dados (em nosso caso, as informações precisam ser convertidas para uma mesma unidade de medida), percepção da função de cada informação matemática na composição da notação (na atividade é necessário saber quem ocupará o numerador e quem ocupará o denominador).
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discuta com a turma:
- Quais as unidades de medidas que aparecem no problema? O que vocês podem perceber em relação às medidas utilizadas em cada informação?
- As medidas são dadas em unidades iguais ou diferentes?
- Da forma em que estão, haverá algum problema para a solução que estamos procurando?
- O que é preciso fazer com essas medidas para continuarmos a buscar a solução do problema?
Discussão das soluções
Tempo sugerido: 18 minutos.
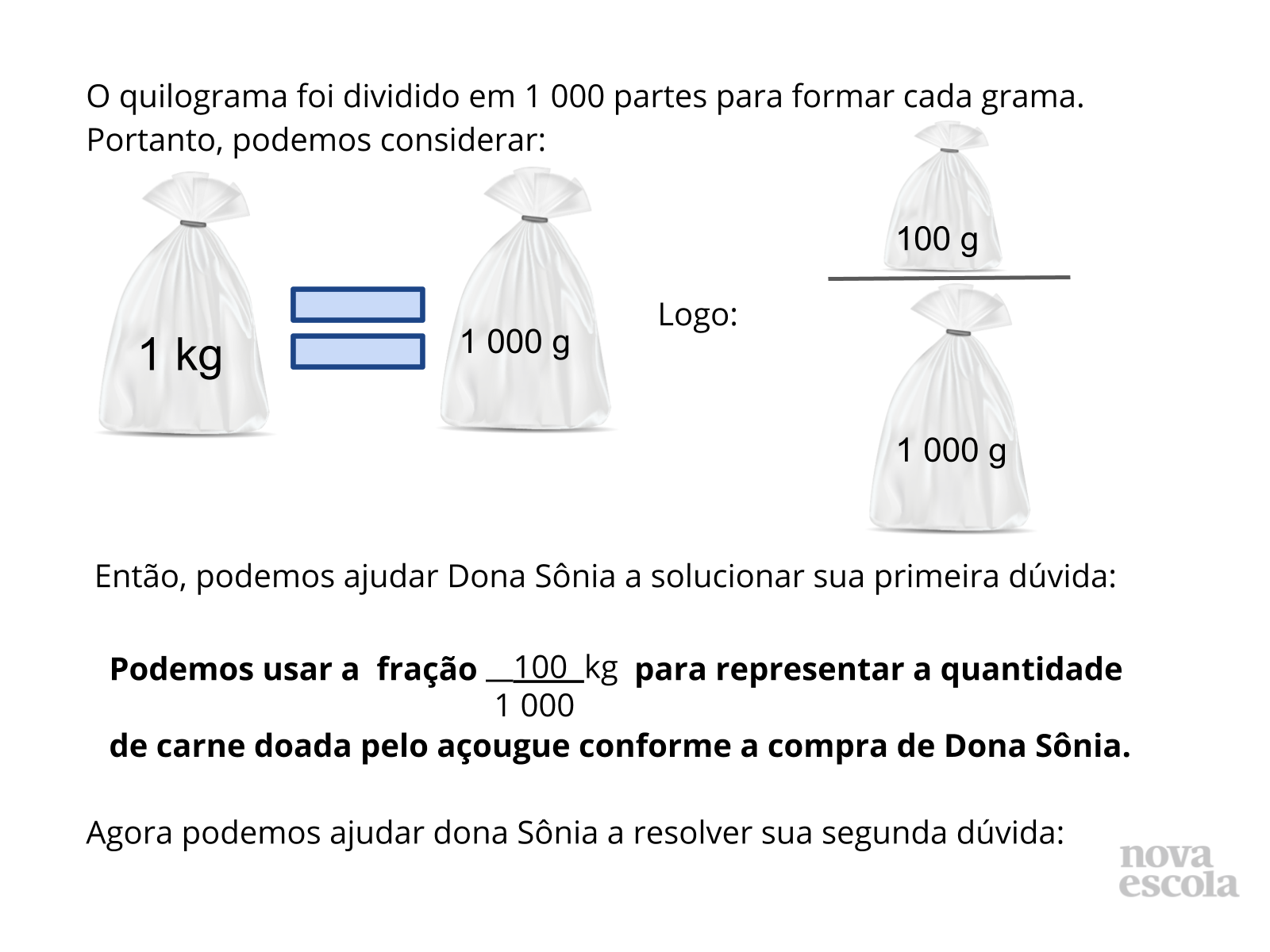
Orientações: Explique que essa fração representa uma razão: de cada 1 000 gramas de carne vendida, serão tomados outros 100 gramas de carne para serem doados.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discussão das soluções
Tempo sugerido: 18 minutos.
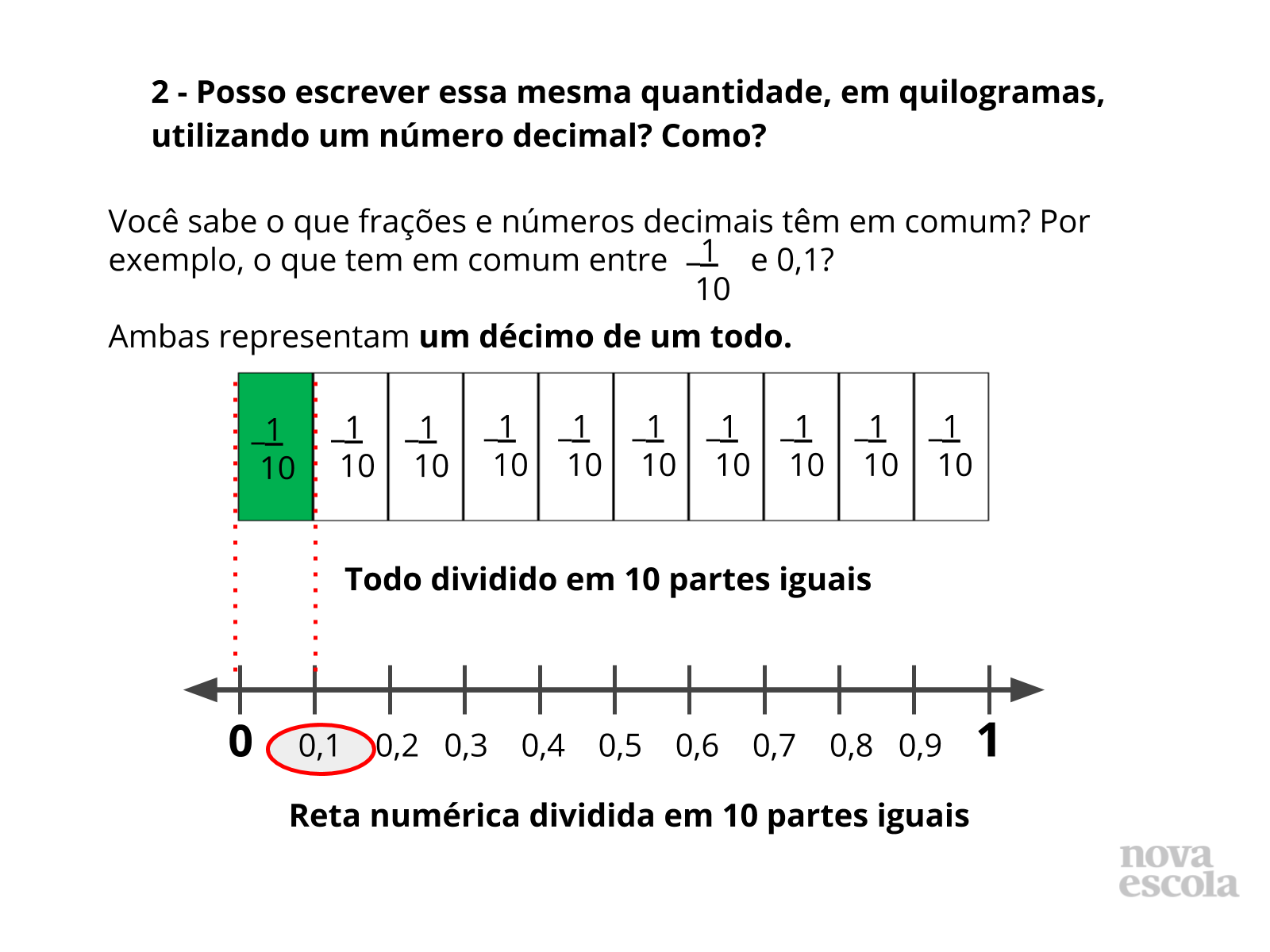
Orientações: Com essa atividade os alunos podem perceber a relação existente entre uma fração e um número decimal e que toda fração pode ser escrita na forma de um número decimal e vice-versa. Reserve tempo para que possam comparar a representação geométrica da fração e a representação do decimal na reta numérica. Leve-os a perceber que ambos foram divididos em 10 partes iguais das quais foi tomada uma parte. Por isso a leitura um décimo. Permita que façam a correspondência com outras frações, como por exemplo 5/10. Assim, poderão perceber que existem duas notações distintas para a mesma quantidade. Lembre os alunos que esse todo pode ser inclusive um conjunto de inteiros (fração de quantidades). Lembre, por exemplo, que 1/2 de um grupo de 10 meninos é igual a 5 meninos.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discussão das soluções
Tempo sugerido: 18 minutos.
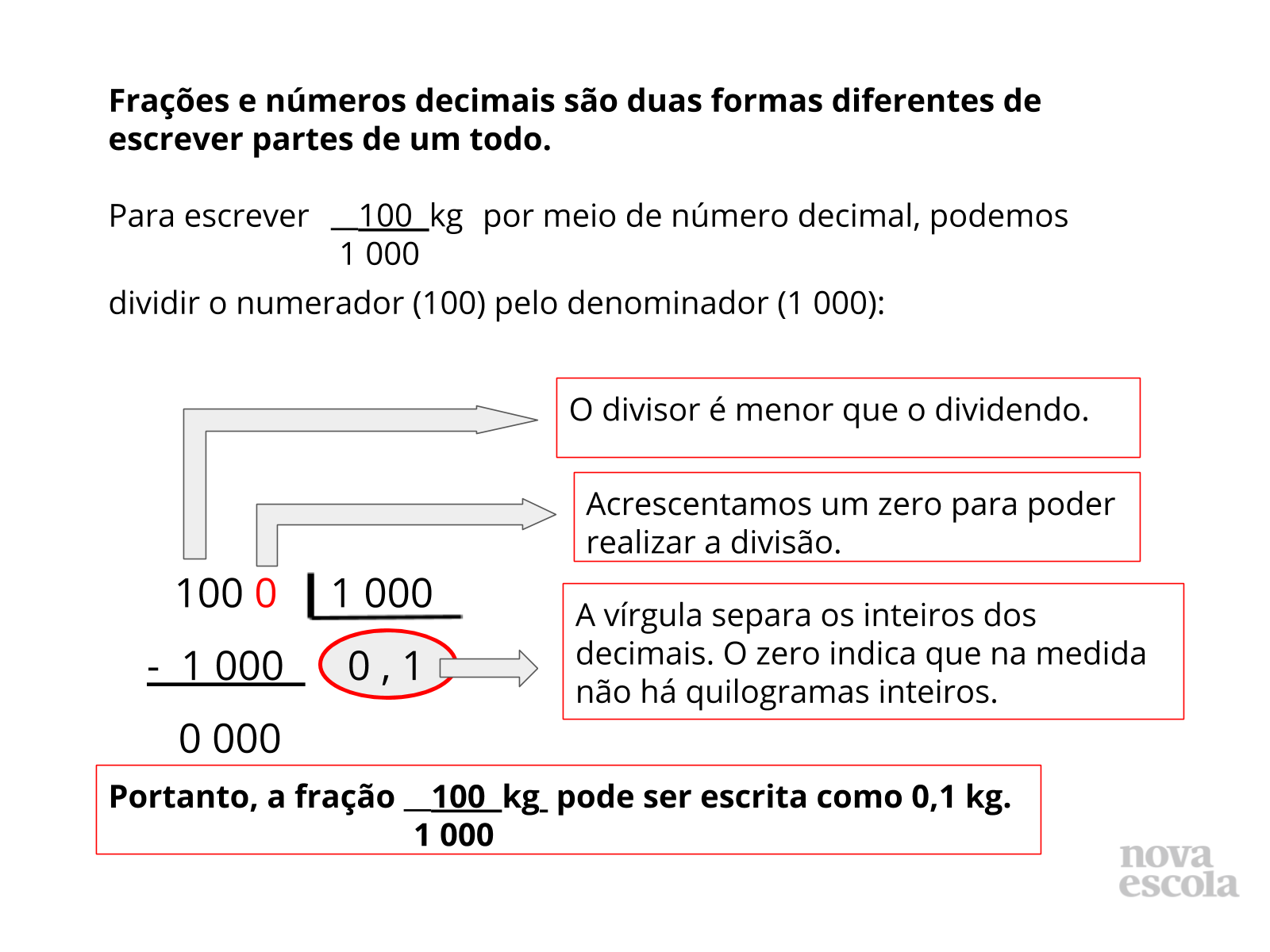
Orientações: O slide anterior permite que os alunos compreendam a relação entre números fracionários e decimais. No entanto, mostre que nem sempre será adequado utilizar representação geométrica e reta numérica para encontrar a correspondência entre as duas notações. Portanto, a divisão do numerador pelo denominador precisa ser encarada como um algoritmo útil para realizar tal correspondência de forma mais rápida e prática. No entanto, é interessante que compreendam o sentido da correspondência como feito no slide anterior e não seja somente memorizado o algoritmo mecanicamente.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discuta com a turma:
- Como podemos escrever 100/1 000 kg por meio de números decimais?
Discussão das soluções
Tempo sugerido: 18 minutos.
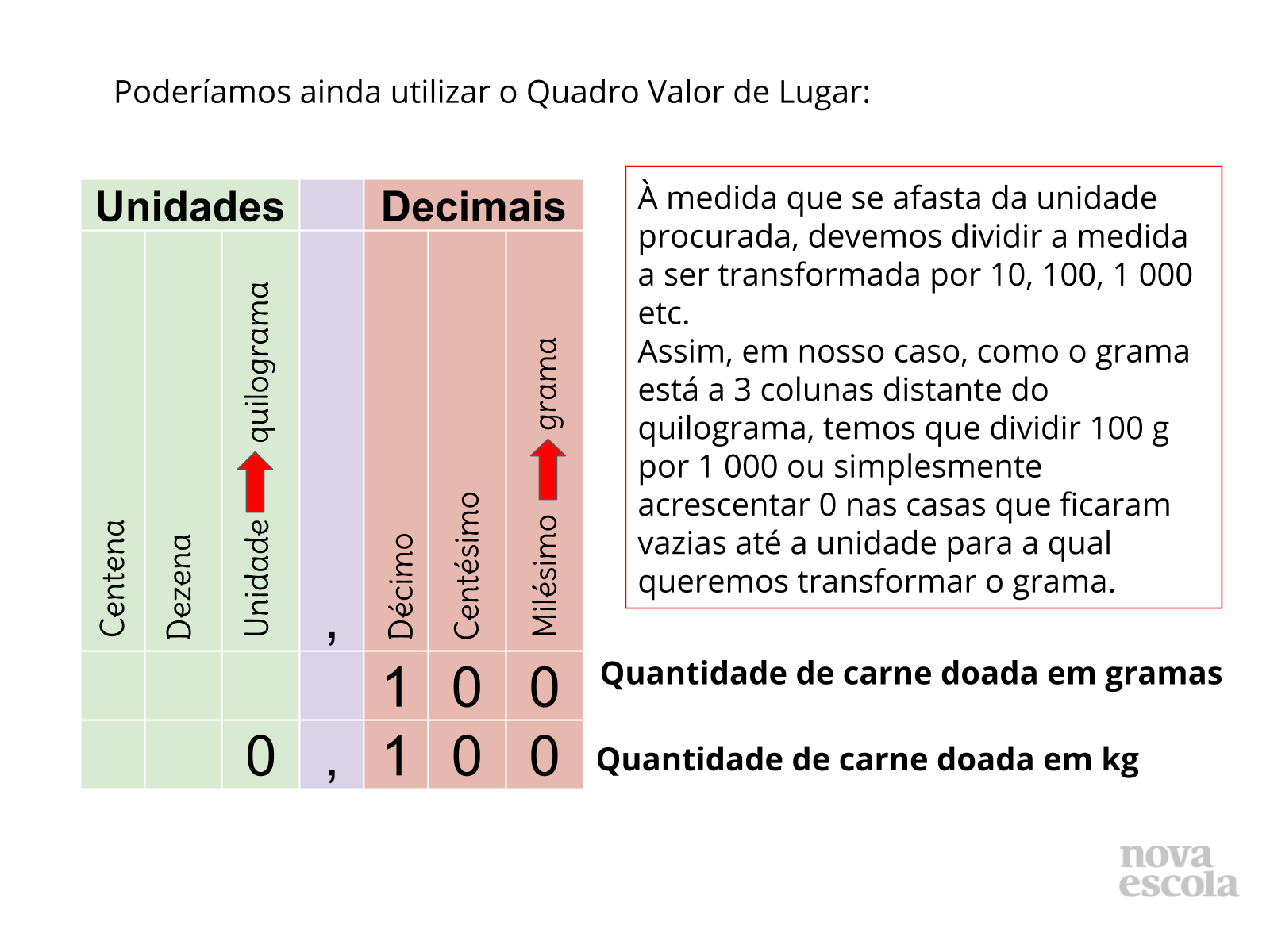
Orientações: Chame atenção para o fato de que, se a transformação é feita de uma unidade inferior (como no caso da atividade) para a superior, realiza-se divisões por 10, 100, 1 000, etc. Porém, se a transformação ocorrer de uma unidade superior para uma inferior, realiza-se a multiplicação.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discussão das soluções

Tempo sugerido: 18 minutos.
Orientações: Nesse slide o professor deve ajudar o aluno a construir a compreensão dos motivos pelos quais ocorrem as divisões ou multiplicações sucessivas à medida que afasta-se de uma unidade à outra. Na verdade, como segue o sistema numérico decimal, as unidades de medida apresentadas nessa aula constituem seus múltiplos e submúltiplos por meio da formação de grupos de dez unidades.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discuta com a turma:
- Por que, à medida que se afasta de uma unidade de medida procurada, devemos realizar sucessivas divisões por 10?
Discussão das soluções

Tempo sugerido: 18 minutos.
Orientações: Nessa questão os alunos devem selecionar, em um conjunto de dados, aquele que interfere na variação de um dado dependente. Deixe que explorem todos os dados anotados e que discutam com os colegas sobre essa relação entre dados dependentes e independentes. Peça outros exemplos: salário e horas trabalhadas, nota na prova e horas de estudos, condições de vida e número de irmãos, etc.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discussão das soluções
Tempo sugerido: 18 minutos.
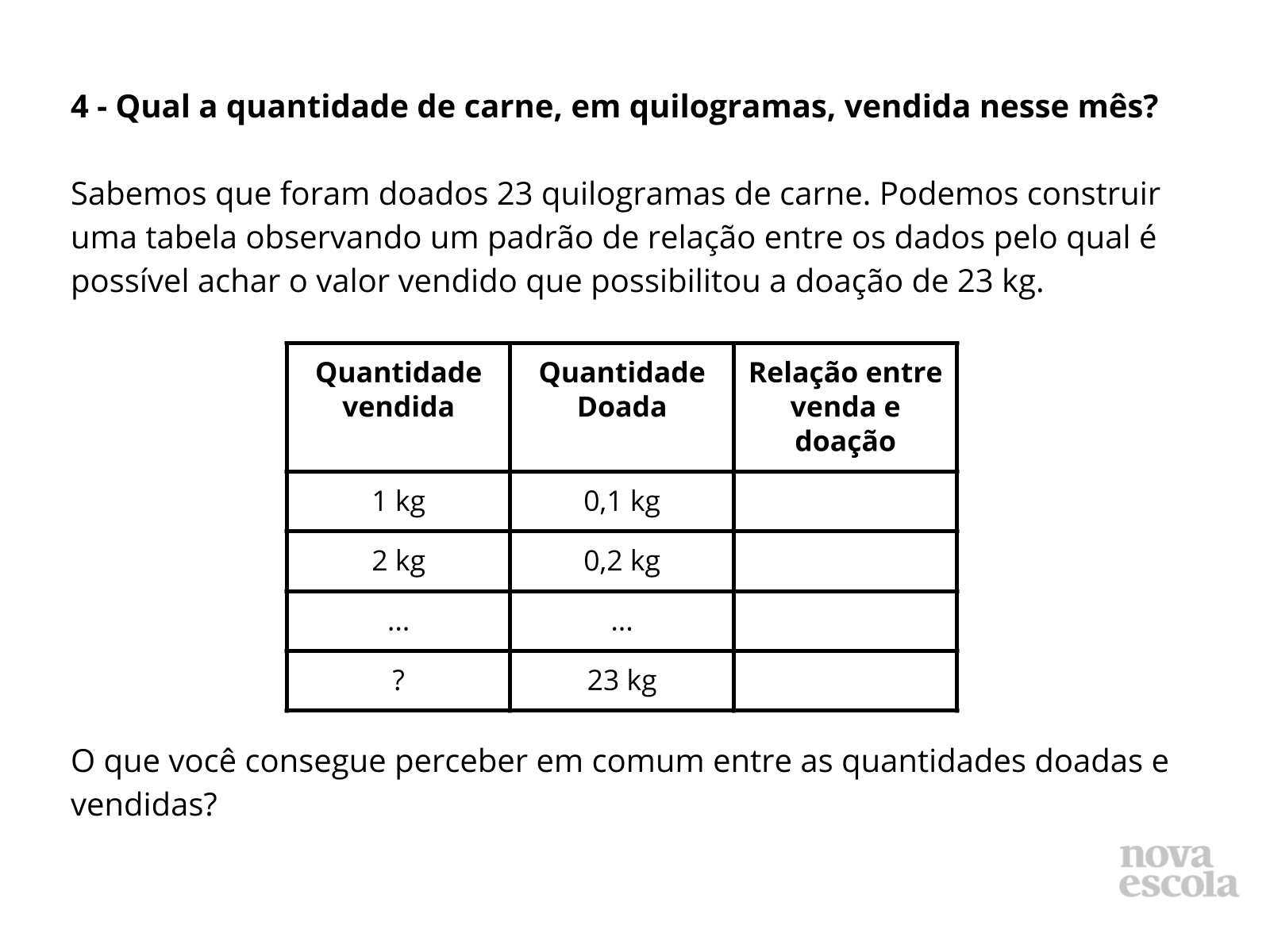
Orientações: A solução da questão anterior será primordial para os alunos compreenderem a questão 4. Essa solução nos leva a saber que, quanto mais carne for vendida, mais será doada. Ao buscar por padrões que determinam a relação entre quantidade vendida e quantidade doada, os alunos poderão perceber que podemos encontrar informações a partir da repetição de tais padrões.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Discuta com a turma:
- Como podemos utilizar a resposta da dúvida 3 para encontrar a solução da dúvida 4?
- O que vocês podem perceber o observar a quantidade de carne vendida e a quantidade de carne doada? Tem algo em comum acontecendo à medida que aumenta-se a quantidade de carne vendida? O que está acontecendo? Como os números estão se modificando?
Discussão das soluções

Tempo sugerido: 18 minutos.
Orientações: Existem outras formas mais complexas para se chegar à solução e que podem não estar ao alcance dos alunos, como a utilização de equações. No entanto, o professor pode explorar estratégias diferentes dessa utilizadas pelos alunos.
Propósito: Discutir as estratégias formuladas pelos alunos de modo a identificar equívocos, levantar possibilidades de soluções e construir ferramentas matemáticas apropriadas para solucionar as questões.
Encerramento

Tempo sugerido: 3 minutos.
Orientações: A aula deve ser concluída com a retomada dos principais conhecimentos pretendidos. Antes de apresentar esse slide, permita que falem o que aprenderam com a aula de hoje.
Propósito: Concluir a aula resumindo os conhecimentos produzidos.
Raio X

Tempo sugerido: 5 minutos.
Orientações: Individualmente, os alunos irão relacionar o problema apresentado ao problema trabalhado durante a aula. Desse modo, o professor poderá verificar se os alunos compreenderam as estratégias que podem ser utilizadas para escrever medidas por meio de notações fracionárias e decimais.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante. Acesse aqui a resolução dessa atividade.
Materiais complementares
Sugestão de adaptação para ensino remoto
Código do plano MAT5_21GRM03
Recursos
- Necessários: -
- Opcionais: -
Para este plano, foque na etapa Retomada e Atividade principal
Retomada
Professor(a), você pode realizar a Retomada deste plano com seus alunos, seja em uma aula síncrona ou assíncrona. Compartilhe com a turma o slide presente nesta atividade e solicite que tentem resolver o problema. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas resoluções e, caso esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas considerações/reflexões em formato de texto ou áudio.
Atividade principal
Professor(a), compartilhe com a turma os slides presentes nesta atividade e solicite que tentem responder os questionamentos. Você pode enviar o documento com a atividade caso considere mais viável, você o encontra aqui: https://nova-escola-producao.s3.amazonaws.com/QqfCd4JFM4DKSqR79CUjTUujnBEu9d6QuvYWh28bJGRkgeCH85jFZvS4RsXp/ativaula-mat5-21grm03.pdf. Envie, em formato de texto, os questionamentos presentes no “Discuta com a turma”. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas resoluções e caso esteja ocorrendo de forma assíncrona os estudantes podem enviar suas considerações/reflexões em formato de texto ou áudio.
Discussão das soluções
Professor(a), talvez, nesse momento de aulas remotas, não seja a melhor estratégia compartilhar com os alunos os slides da “Discussão das soluções”. Sugerimos que você grave um vídeo explicando e comentando a solução e nele mostre as imagens e conclusões dos slides. Caso o envio do vídeo não seja possível, você pode compartilhar as imagens e explicar com um áudio ou texto cada um dos slides. Você pode sugerir que os alunos façam as divisões na calculadora e analisem o que ocorre com os números e a posição da vírgula.
Encerramento
Professor(a), compartilhe com os alunos a imagem a seguir e solicite que os estudantes escrevam, com suas palavras, o que compreenderam da relação entre a vírgula, a divisão por 10, 100 e 1000 e a relação entre gramas e quilogramas.
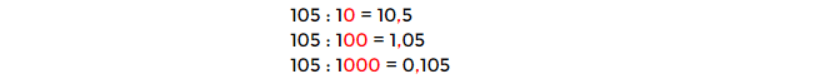
Raio X
O problema proposto no Raio X pode ser enviado aos alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma. Os alunos podem gravar um vídeo explicando suas resoluções.
Convite às famílias
Professor(a), sugira que os alunos socializem com seus familiares o que aprenderam nesta aula sobre transformações de unidades de medida. Sugira que os alunos, juntos com seus familiares, façam a atividade proposta no Raio X deste plano. Eles podem medir seus antebraços, comparar o tamanho e realizar a transformação pedida na atividade.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alexandre Tolentino de Carvalho
Mentor: Fábio Menezes da Silva.
Especialista de área: Fernando Barnabé
Habilidade da BNCC
EF05MA19 - Resolver e elaborar problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais.
Objetivos específicos
- Representar unidades de medidas utilizando notação fracionária e notação decimal.
- Relacionar a transformação de medidas por meio do algoritmo usual ou por meio de divisões sucessivas por 10 relacionando-a com o deslocamento da vírgula.
- Solucionar problemas por meio de investigação de padrões.
Conceito-chave
Notação fracionária e decimal de medidas.
Recursos necessários
- Lápis,
- Borracha,
- Caderno,
- Régua,
- Q.V.L.












