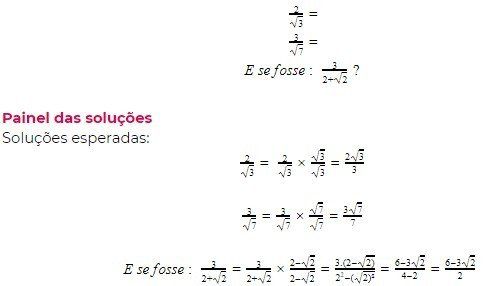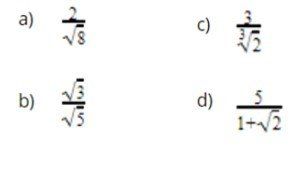Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Propósito: Esclarecer o objetivo aos estudantes.
Orientação: Apresente o objetivo aos alunos.
Discuta com a turma:
Aquecimento

Tempo sugerido: 8 minutos.
Propósito: Rever os padrões relacionados à distributiva em expressões com radicais.
Orientação: Faça uma demonstração aos estudantes atentando ao padrão das raízes que quando elevadas ao índice da raiz resultam no radicando sem raiz.
Discuta com a turma:
- Qual a relação entre o sinal das raízes com a ideia de se obter um valor racional para a área?
- Materiais complementares:
Atividade aquecimento
Resolução Atividade aquecimento
Atividade principal

Tempo sugerido: 18 minutos (Slides 4 a 7).
Orientação: Apresente aos estudantes os dois exemplos e os questione sobre as diferenças entre eles.
Propósito: Exemplificar uma situação em que a racionalização é necessária.
Discuta com a turma:
- Qual a diferença de se dividir por um número racional e por um irracional?
- Materiais complementares:
Atividade principal
Resolução atividade principal
Guia de intervenção
Atividade principal

Tempo sugerido: 18 minutos (Slides 4 a 7).
Orientação: Destaque elementos importantes, como a escolha dos fatores de acordo com o denominador, e a ideia do elemento neutro, mantendo o mesmo valor. Destaque aos estudantes a ideia de que a ideia principal é a potência precisa ser igual ao índice da raiz.
Propósito: Apresentar o processo de racionalização.
Discuta com a turma:
- Multiplicar algum número por 1 altera seu valor?
Atividade principal

Tempo sugerido: 18 minutos (Slides 4 a 7).
Orientação: Discuta com os alunos este outro caso de racionalização, questionando diferenças e semelhanças com o caso anterior. É interessante retomar o que foi visto na atividade de retomada, para deixar mais claro a ideia da escolha do fator de racionalização.
Propósito: Apresentar outro caso de racionalização.
Discuta com a turma:
- O que aconteceria se o sinal do radical fosse negativo?
Atividade principal

Tempo sugerido: 18 minutos (Slides 4 a 7).
Orientação: Apresente aos estudantes os exercícios acima. Questione sobre possíveis detalhes que os alunos precisam tomar cuidado.
Propósito: Aplicar os conhecimentos sobre racionalização.
Discuta com a turma:
- Qual a justificativa para utilizar a racionalização?
Discussão das soluções

Tempo sugerido: 12 minutos (Slides 8 a 11).
Orientação: Saliente aos estudantes o objeto da racionalização, que é exatamente tornar o denominador um número racional
Propósito: Resolver o primeiro exercício.
Discuta com a turma:
- Qual característica numa expressão demonstra a necessidade de racionalização?
Discussão das soluções

Tempo sugerido: 12 minutos (Slides 8 a 11).
Propósito: Resolver o caso de raiz no denominador.
Orientação: Professor, questione aos estudantes qual o critério utilizaram para resolver este problema. Pergunte como fizeram para encontrar o melhor fator. A cada passo, peça a um aluno ou uma aluna ir à lousa para mostrar como resolver.
Discuta com a turma:
- Existe alguma característica marcante no fator de multiplicação?
Discussão das soluções

Tempo sugerido: 12 minutos (Slides 8 a 11).
Propósito: Resolver o caso em que se encontra soma com raiz no denominador.
Orientação: Questione os estudantes se seria possível escolher um fator apenas com raízes neste caso. Se achar necessário retome a ideia da retomada. A cada passo, peça a um aluno ou uma aluna ir à lousa para mostrar como resolver.
Discuta com a turma:
- Como podemos escolher o fator para deixar o denominador racional?
Discussão das soluções

Tempo sugerido: 12 minutos (Slides 8 a 11).
Propósito: Resolver o caso em que se encontra subtração com raiz no denominador.
Orientação: Questione os estudantes se seria possível escolher um fator apenas com raízes neste caso. Se achar necessário retome a ideia da retomada. A cada passo, peça a um aluno ou uma aluna ir à lousa para mostrar como resolver.
Discuta com a turma:
- Como podemos escolher o fator para deixar o denominador racional?
- Qual o padrão para escolher o sinal das raízes?
Encerramento

Tempo sugerido: 2 minutos.
Propósito: Rever o objetivo da aula verificando os tópicos abordados.
Orientação: Discuta com os alunos os pontos da aula.
Discuta com a turma:
- O objetivo da aula foi alcançado?
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.