Atividade principal
Plano de Aula
Plano de aula: Explorando os restos das divisões
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Sequencia numérica recursiva formada por múltiplos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Márcia Regina Kaminski
Mentora: Carla Simone de Albuquerque
Revisora Pedagógica: Eliane Zanin
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
(EF04MA12) Reconhecer, por meio de investigações, que há grupos de números naturais para os quais as divisões por um determinado número resultam em restos iguais, identificando regularidades.
Objetivos específicos
Identificar padrões e regularidades em restos das divisões de um número natural por outro número natural.
Conceito-chave
Sequência numérica recursiva formada por múltiplos de um número natural.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Datashow ( opcional ).
Habilidades BNCC:
Objetivos de aprendizagem
Identificar padrões e regularidades em restos das divisões de um número natural por outro número natural.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Aula
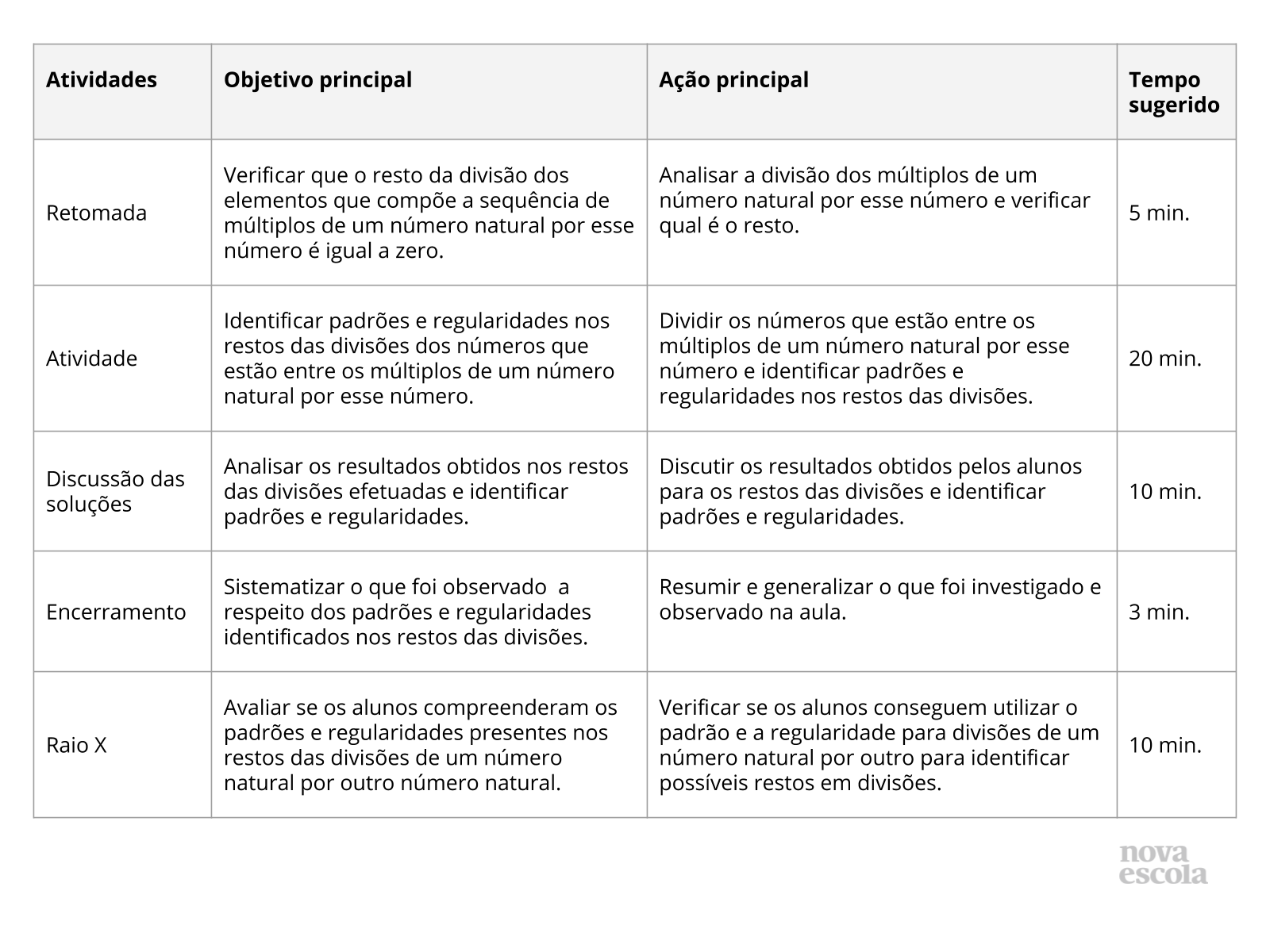
Resumo da aula
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.