Resumo da aula
Orientações:
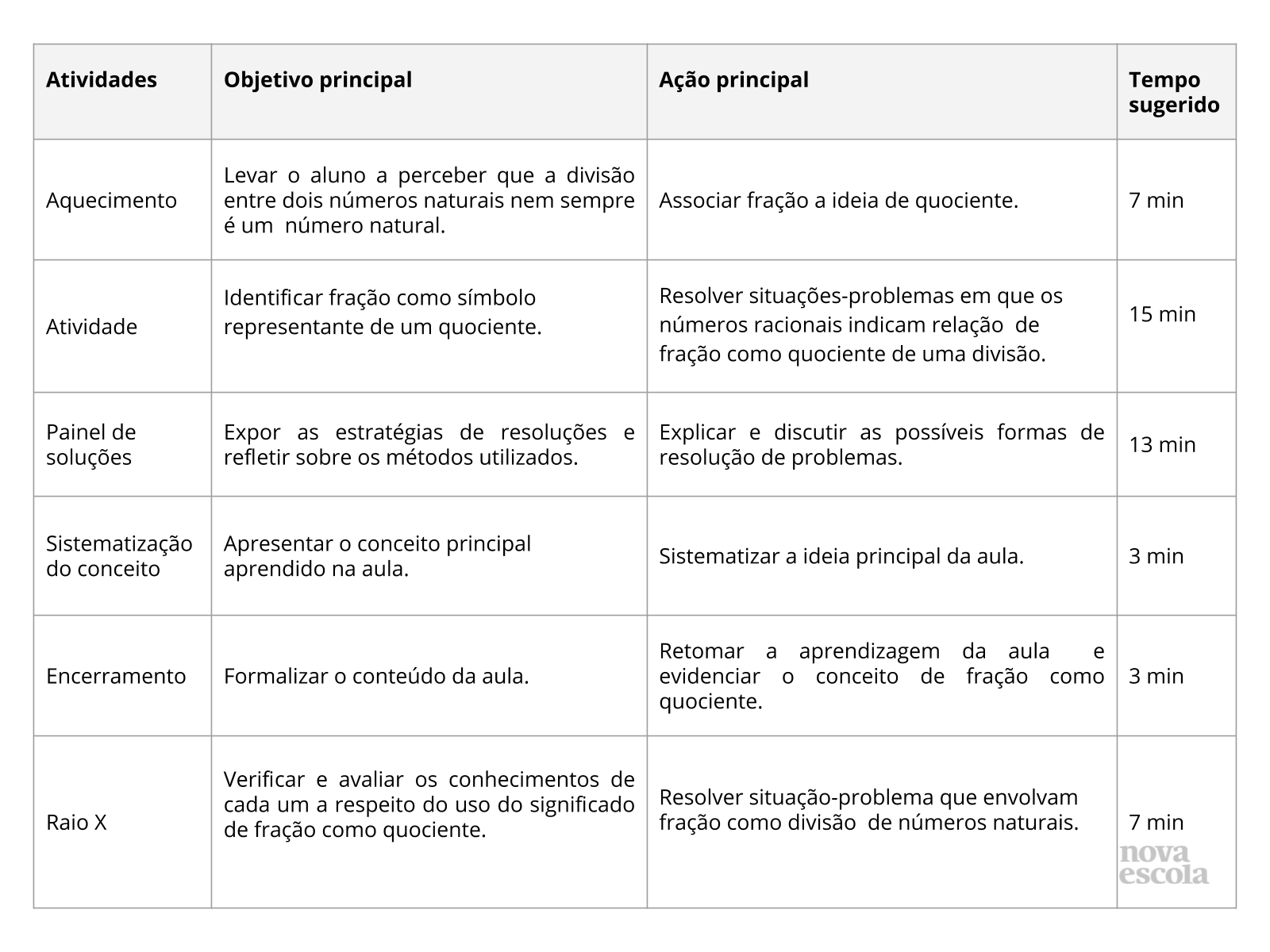
Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
Tempo sugerido: 3 minutos.
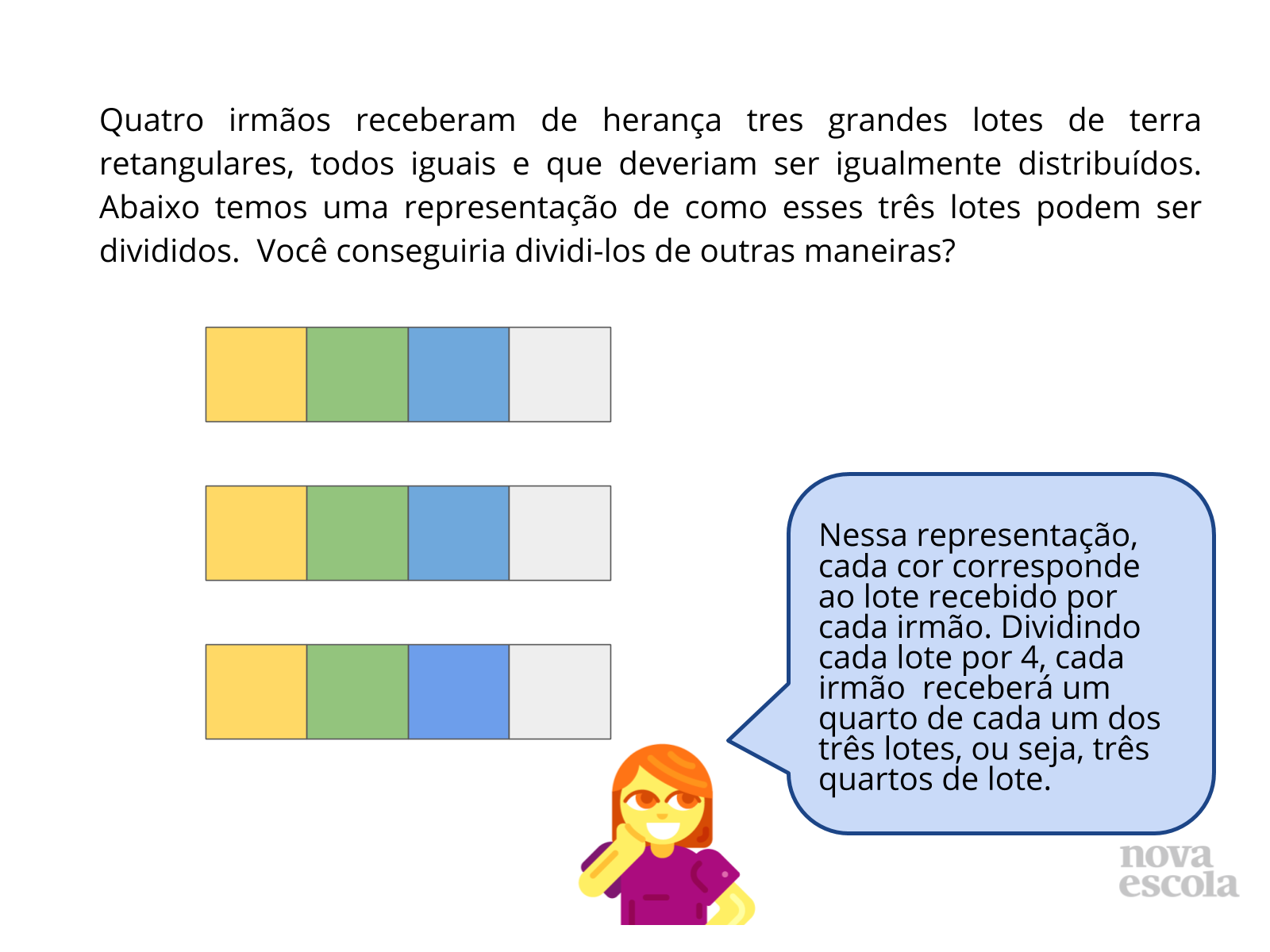
Orientações: Inicie a aula mostrando este probleminha e uma possível resposta. Pergunte aos alunos: Esta é a única forma de fazer a divisão? Como eles fariam para dividir estes terrenos? Anote as respostas deles no quadro e peça que eles expliquem.
Propósito: Compreender a fração como uma divisão.
Discuta com a turma:
- Como faríamos para dividir entre os quatro irmaos?
- Como poderíamos representar através de frações o que cada pessoa recebeu?
- Teria outra forma de dividir os terrenos?
- Qual a fração da herança coube a cada irmão?
Materiais complementares:
Aquecimento
Resolução do aquecimento
Atividade principal (slides 4 e 5)

Tempo sugerido: 15 minutos.
Orientação: Confirme que todos entenderam a divisão ocorrida no aquecimento. De exemplos do cotidiano, em que ocorre divisão não exata. Ressalte que a fração pode ser usada como resposta de uma divisão não exata. Avise que eles farão um problema. Oriente-os a refletir com calma sobre o problema, sem se preocupar em chegar ao resultado. Explique que o importante é propor estratégias para abordar o problema e então testá-las. Você poderá escrever o texto do problema no quadro, projetá-lo ou entregar uma cópia aos alunos. Peça aos para estudantes que leiam o problema, dê tempo para que tentem resolvê-lo, junto com um colega. Não faça nenhuma intervenção neste momento, observe como eles organizam e representam os dados do problema e quais as estratégias que eles utilizam.
Propósito: Incentivar os alunos para que mobilizem os conhecimentos que já possuem de fração como quociente para resolver o problema proposto. Fazer com que os alunos usem de estrategias proprias utilizando dos conhecimentos que já possuem de frações para resolver o problema proposto.
Discuta com a turma:
- Quantas balas a mais cada aluno recebeu?
- É possível escrever usando um número inteiro a quantidade de saquinhos de bala que cada aluno levou para casa?
- Considerando cada saquinho de 10 balas como um inteiro, como você pode representar numericamente a quantidade de saquinhos de bala que cada aluno recebeu?
- Qual estratégia usou para chegar a este resultado?
Atividade principal (slides 4 e 5)

Tempo sugerido: 15 minutos.
Orientação: Confirme que todos entenderam a divisão ocorrida no aquecimento. De exemplos do cotidiano, em que ocorre divisão não exata. Ressalte que a fração pode ser usada como resposta de uma divisão não exata. Avise que eles farão um problema. Oriente-os a refletir com calma sobre o problema, sem se preocupar em chegar ao resultado. Explique que o importante é propor estratégias para abordar o problema e então testá-las. Peça aos para estudantes que leiam o problema, dê tempo para que tentem resolvê-lo, junto com um colega. Não faça nenhuma intervenção neste momento, observe como eles organizam e representam os dados do problema e quais as estratégias que eles utilizam.
Propósito: Incentivar os alunos para que mobilizem os conhecimentos que já possuem de fração como quociente para resolver o problema proposto. Fazer com que os alunos usem de estrategias proprias utilizando dos conhecimentos que já possuem de frações para resolver o problema proposto.
Discuta com a turma:
- Quantas balas a mais cada aluno recebeu?
- É possível escrever usando um número inteiro a quantidade de saquinhos de bala que cada aluno levou para casa?
- Considerando cada saquinho de 10 balas como um inteiro, como você pode representar numericamente a quantidade de saquinhos de bala que cada aluno recebeu?
- Qual estratégia usou para chegar a este resultado?
Materiais complementares:
Atividade principal
Resolução do atividade principal
Guia de intervenção
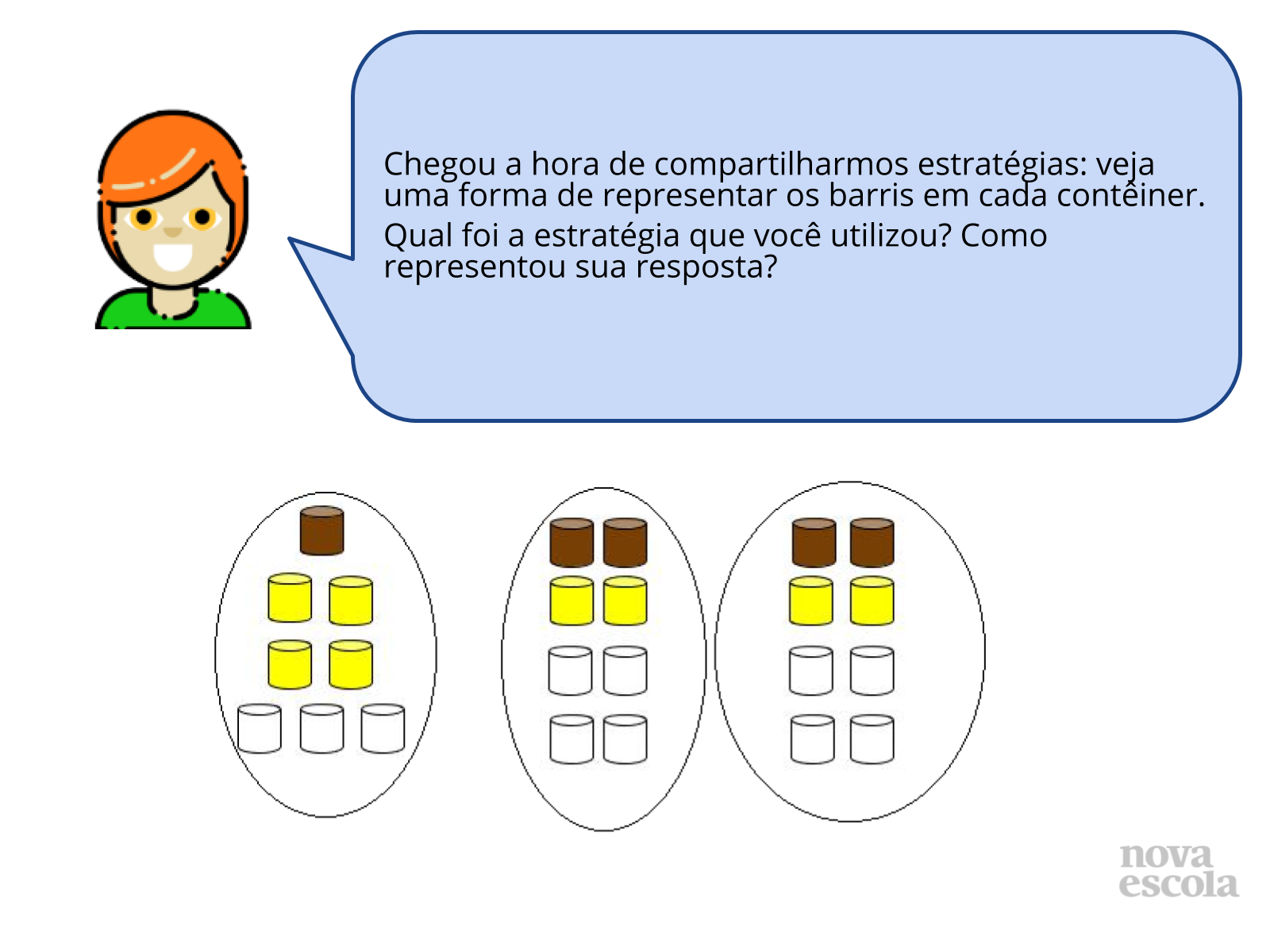
Painel de soluções

Tempo sugerido: 13 minutos.
Orientações: Peça aos alunos que compartilhem as estratégias que usaram, registrando na lousa . Mostre a eles que nos dois casos mostrados nos slides há erro. No primeiro não há a resposta de quanto cada aluno recebeu AO TODO. No segundo há o total de balas, mas não o total DE SAQUINHOS que cada aluno recebeu.
Propósito: Realizar um fechamento das ideias discutidas até o momento.
Discuta com a turma:
- Alguém chegou em uma solução diferente dessa?
- Você poderia explicar como fez?
- Qual caminho você utilizou para chegar a quantidade de balas para cada um?
- Será que existe outro caminho para resolver ?
- É necessário fazer este problemas por etapas? Por que?
- Alguém fez uma representação desta situação?
Sistematização do conceito

Tempo sugerido: 3 minutos.
Orientações: Leia o slide de sistematização e deixe que os alunos exponham suas impressões e conclusões.
Propósito: Sistematizar o conteúdo aprendido. Mostrar duas formas de escrever a resposta para a mesma divisão.
Encerramento

Tempo sugerido: 3 minutos.
Orientação: Peça aos alunos que concluam em um parágrafo o que aprenderam, e construa com a turma o resumo final. É essencial que eles percebam a relação que existe entre fração e divisão.
Propósito: Retomar a aprendizagem da aula e evidenciar o conceito de fração como quociente.
Raio x
Tempo sugerido: 7 minutos.
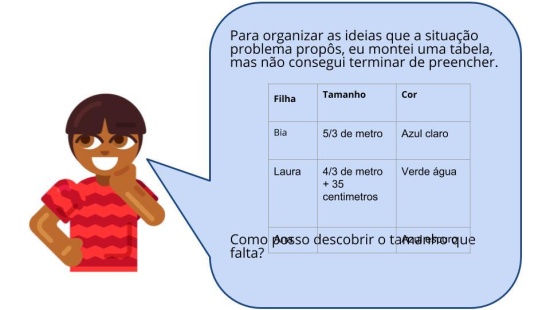
Orientações: Apresente a nova situação e peça que os estudantes leiam o problema e resolvam. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. Após apresentar a nova situação, circule pela sala, para verificar como estão montando as representações. Você pode projetar, passar no quadro ou fazer cópia para os alunos. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da relação do conceito de fração com o quociente de uma divisão.
Discuta com a turma:
- Você entendeu o que o problema propos?
- Como fez para identificar o tamanho do elástico de cada menina?
- Como chegou a resposta?
- Voce conseguiu representar este problema? De que forma?
- Qual seria a forma mais prática de resolver esse problema?
Raio X para impressão
Resolução do atividade principal
Atividade complementar
Resolução da Atividade complementar