Resumo da aula
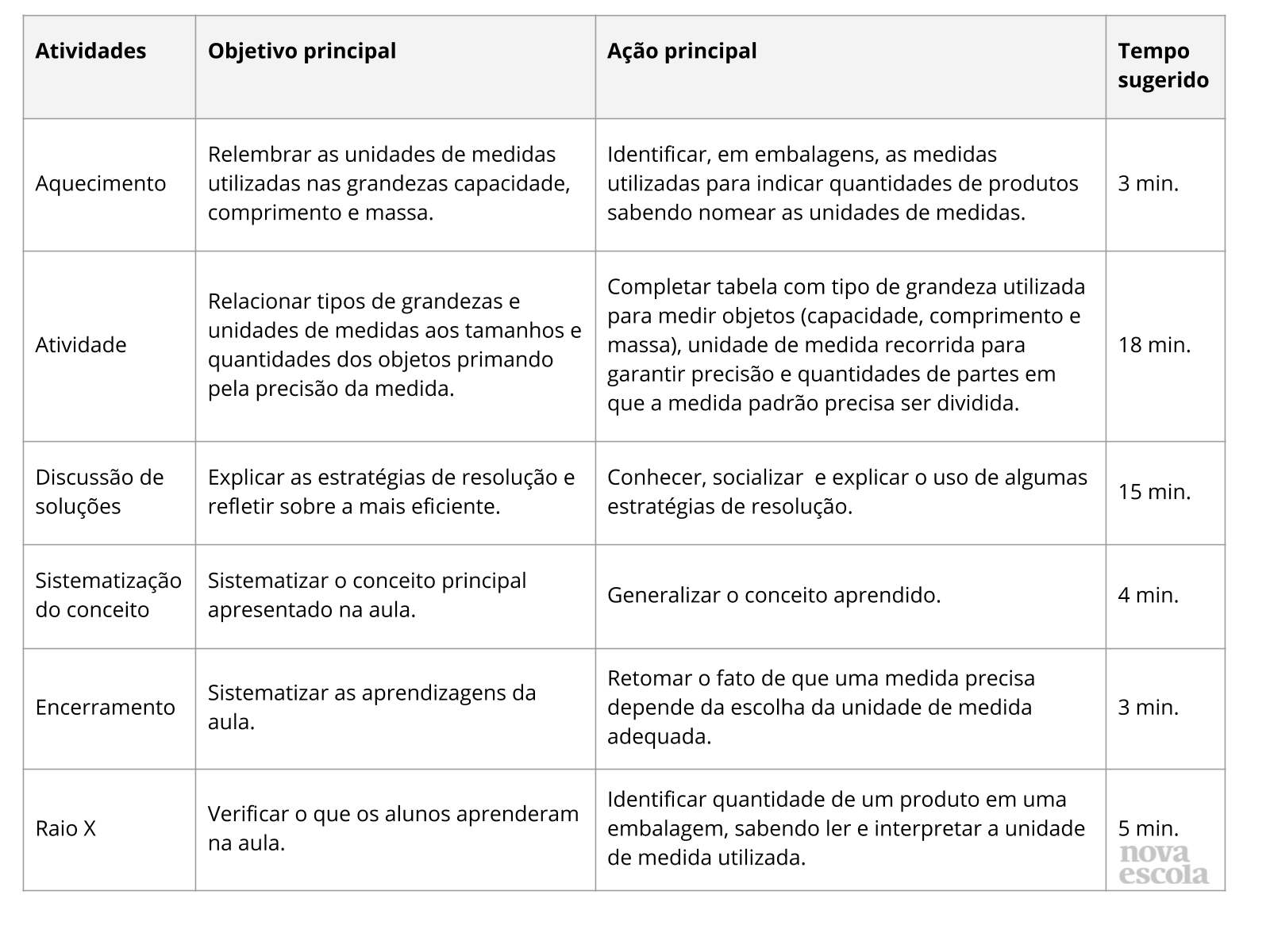
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 3 minutos.
Orientação: Busque deixar a turma à vontade para levantar conjecturas e apresentar formas alternativas de medir os produtos, por ex.: uma colher de manteiga, um copo de suco. No entanto, levem-nos a relembrar as formas de medidas convencionais.
Propósito: Relembrar alguns conceitos prévios importantes para as aprendizagens propostas nessa aula.
Discuta com a turma:
- Como podemos ler a quantidade de produto informado nas embalagens?
- Que tipo de medida está sendo feita em cada embalagem? Em alguma delas está sendo medido o comprimento? Em alguma está sendo medida a massa? Alguma está medindo líquidos?
- Vocês se lembram o que é uma medida padrão? Qual dos produtos está sendo medido pela unidade padrão? Em qual essa medida não é feita pela unidade padrão? Qual seria a unidade padrão dessas medidas?
Atividade principal
Tempo sugerido: 18 minutos.
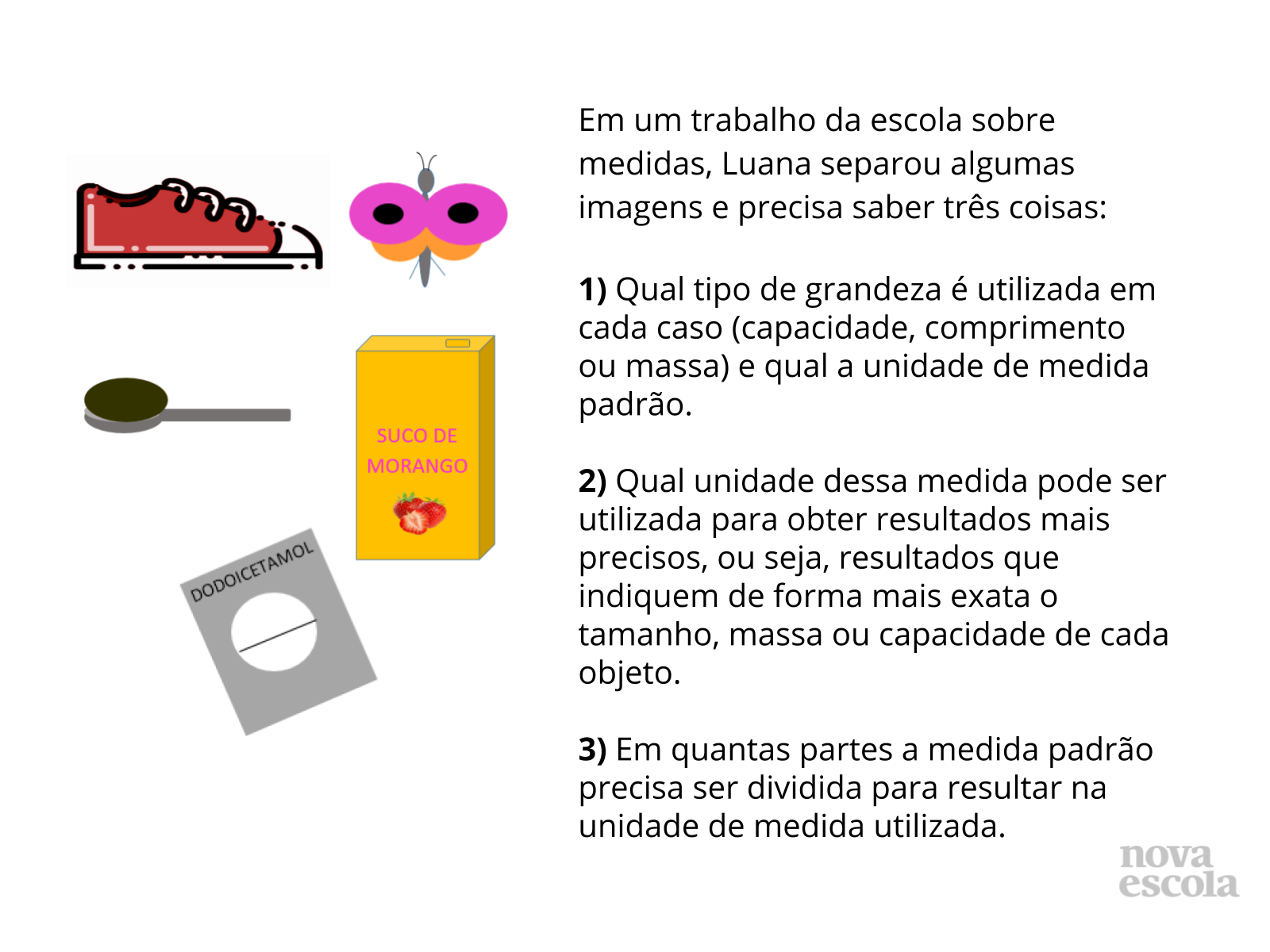
Orientação: Se possível, entregue para os alunos pedaços de barbantes ou ripas de um metro de comprimento e peça para medir o tamanho de seu tênis, sapato ou sandália. Informe aos alunos que esse instrumento de medida (barbante ou ripa) tem exatamente um metro de comprimento. O alunos perceberão que o instrumento é inapropriado para medir o calçado por ser uma medida maior que o objeto medido.
Deixe os alunos explorarem cada imagem, pedindo para que imaginem o tamanho real de cada objeto. Outras formas de medidas podem aparecer, como polegada, tamanho da forma do sapato, etc. Explore essas medidas buscando mencionar as medidas convencionais (metro, quilograma, litro) como medidas formais, não mais importantes do que as demais.
Propósito: Permitir que os alunos consigam, por meio do esforço produtivo, relacionar tipos de grandezas e unidades de medidas aos tamanhos e quantidades dos objetos primando pela precisão da medida.
Discuta com a turma:
- Que tipo de grandeza pode ser utilizada para medir os objetos? Vocês se recordam das unidades padrão dessas grandezas?
- Qual unidade de medida deve ser utilizada para medir uma corda grande? Essa medida é útil para medir também o comprimento de um tênis? Por quê?
- O que devemos fazer com as unidades padrão para medir objetos menores que elas?
Materiais complementares para impressão:
Atividade principal
Resolução da atividade principal
Guia de intervenção
Atividade principal

Tempo sugerido: 18 minutos.
Orientação: Peça para os alunos se organizarem em duplas. Depois permita que discutam e registrem nas tabelas as informações faltantes. O interessante é que percebam que algumas medidas necessitam de uma unidade menor do que a medida padrão.
Se possível, forneça ou deixe que explorem no ambiente objetos reais como sapatos, colheres, cordas e comprimidos, permitindo que manipulem tais objetos levando-os a encontrar as informações necessárias.
Propósito: Permitir que os alunos consigam, por meio do esforço produtivo, relacionar tipos de grandezas e unidades de medidas aos tamanhos e quantidades dos objetos primando pela precisão da medida.
Discuta com a turma:
- Que tipo de grandeza pode ser utilizada para medir os objetos (comprimento, capacidade, massa) pedindo para que se recordem sobre a medida padrão de cada grandeza.
- Qual unidade de medida deve ser utilizada para se obter uma mensuração mais precisa. As unidades padrão são adequadas para medir objetos pequenos?
- Durante a discussão, leve os alunos a perceber que as medidas padrão precisam ser divididas em partes menores para serem usadas na mensuração de objetos e substâncias pequenas.
- Outras formas de medidas podem aparecer, como polegada, tamanho da forma do sapato, etc. Explore essas medidas buscando mencionar as medidas convencionais (metro, grama, litro) como medidas formais, não mais importantes do que as demais.
Discussão de soluções

Tempo sugerido: 15 minutos.
Orientações: Permita que os alunos compartilhem suas soluções com os demais colegas de turma. Peça para identificarem semelhanças e as diferentes formas de solucionar a questão. Em seguida, passe para estes slides. Nele, os alunos poderão comparar suas respostas ao modelo fornecido pela personagem. Ofereça oportunidades para que os alunos possam participar, realizando conexões com os objetos do dia a dia em que podem utilizar os tipos de medidas trabalhados. Discuta com eles sobre formas alternativas de medir que apresentarem em suas soluções relacionando-as às medidas convencionais. Permita que revejam suas respostas buscando analisar se as sugestões de soluções seguiram o modelo da personagem. Apesar de escolhermos as grandezas usualmente utilizadas para medir cada situação, outras grandezas poderiam ser tomadas de cada objeto. Assim, poderíamos por exemplo, medir, além do comprimento do tênis, sua massa (utilizando balança) e sua capacidade (mergulhando o objeto em um tanque e observando a quantidade de água que foi deslocada). Discuta isso com os alunos perguntando: Mas ela poderia medir a massa do tênis? E sua capacidade?
Poderíamos utilizar as unidades padrão para medir os objetos, utilizando ao invés das submúltiplos, frações ou números decimais. No entanto, deixe esse tema para outra aula caso nenhum aluno comente sobre. Nessa aula, foque na possibilidade do uso dos submúltiplos como forma de conferir precisão às medidas.
Propósito: Utilizar as soluções apresentadas pelos alunos para que compreendam as medidas convencionais e seus submúltiplos através da comparação de suas respostas com as respostas da personagem da atividade.
Discuta com a turma:
- Luana escolheu utilizar uma medida menor que a unidade padrão (metro). Por que ela fez essa escolha?
- Por que a menina escolheu não medir o tênis em metros? Quais unidades de medida podemos utilizar para medir esse tênis?
- O que essas unidades têm a ver com o metro?
- Em quantas partes o metro precisou ser dividido para formar cada unidade de medida?
- Qual a necessidade de dividir as medidas padrões em medidas menores?
- Existem outras formas de medir um tênis?
Discussão de soluções

Tempo sugerido: 15 minutos.
Orientações: Em seguida à exploração do modelo apresentado pela personagem, utilize essa série de slides para explorar objetos que podem ser medidos pela unidade de medida padrão e outros que tenham necessidade de serem medidos por meio de submúltiplos. Permita que os alunos façam estimativas sobre as medidas dos objetos antes de apresentar a informação.
Propósito: Explorar objetos que podem ser medidos por meio de unidades de medida padrão e objetos que podem ser medidos por meio de submúltiplos.
Discuta com a turma:
- Uma borboleta tem mais ou menos que um quilograma?
- Qual grandeza utilizamos para medir a massa de uma flor? E qual sua medida padrão?
- Por que algumas pessoas acham que a unidade de medida padrão da massa é o grama e não o quilograma?
- Luana diz que a borboleta pode ser medida em gramas. Quantos gramas vocês acham que uma borboleta tem em média? E uma colher de sopa de achocolatado, tem mais ou menos massa que a borboleta? Quem é mais leve, a borboleta, a colher de sopa de achocolatado ou um comprimido?
- Por que não precisamos usar uma medida menor que o grama para medir a massa da borboleta? Mas poderíamos utilizar uma medida menor que o grama para medir a massa dessa borboleta?
- Quantos gramas você acha que são necessários para formar um quilograma? Deixe-os concluir que precisamos de exatamente 1 000 gramas. Isso significa que, se uma borboleta tivesse 1 grama de massa, precisaríamos de 1 000 borboletas para formar 1 kg desse inseto.
- Qual a necessidade de dividir as medidas padrão em medidas menores?
- Existem medidas menores que a milésima parte? Se sim, por que quase não a conhecemos?
- O que é uma colher de sopa? Existem outros tipos de colheres utilizados como medidas?
Discussão de soluções

Tempo sugerido: 15 minutos.
Orientações: No início desse slide, permita que os alunos percebam que seria mais complicado medir essa quantidade por seu comprimento (com uma régua, por exemplo) ou por sua capacidade (por não ser um líquido).
Propósito: Explorar objetos que podem ser medidos por meio de unidades de medida padrão e objetos que podem ser medidos por meio de submúltiplos.
Discussão de soluções

Tempo sugerido: 15 minutos.
Orientações: Líquidos podem ser medidos por meio de sua capacidade e por meio de sua massa. No entanto, é mais comum encontrar essa medida por meio da grandeza capacidade. Leve a discussão ao ponto dos alunos perceberem que seria um absurdo pensar em comprar, por exemplo, um metro de suco. No entanto, questione-os sobre como as empresas fornecedoras da água que chega até nossa casa cobram seu consumo. Assim, permita que compreendam que essa medida se dá em metros cúbicos que é uma medida de volume diferente da medida de comprimento.
Propósito: Explorar objetos que podem ser medidos por meio de unidades de medida padrão e objetos que podem ser medidos por meio de submúltiplos.
Discussão de soluções

Tempo sugerido: 15 minutos.
Orientações: Informe aos alunos que, apesar da medida padrão ser o quilograma, a unidade de referência para formar os múltiplos e submúltiplos é o grama.
Propósito: Explorar objetos que podem ser medidos por meio de unidades de medida padrão e objetos que podem ser medidos por meio de submúltiplos.
Sistematização do conceito

Tempo sugerido: 4 minutos.
Orientações: Aproveite esse momento para permitir que o aluno generalize suas aprendizagens construídas no decorrer da aula.
Propósito: Sistematizar os principais conceitos apresentados no decorrer da aula.
Encerramento
Tempo sugerido: 3 minutos.
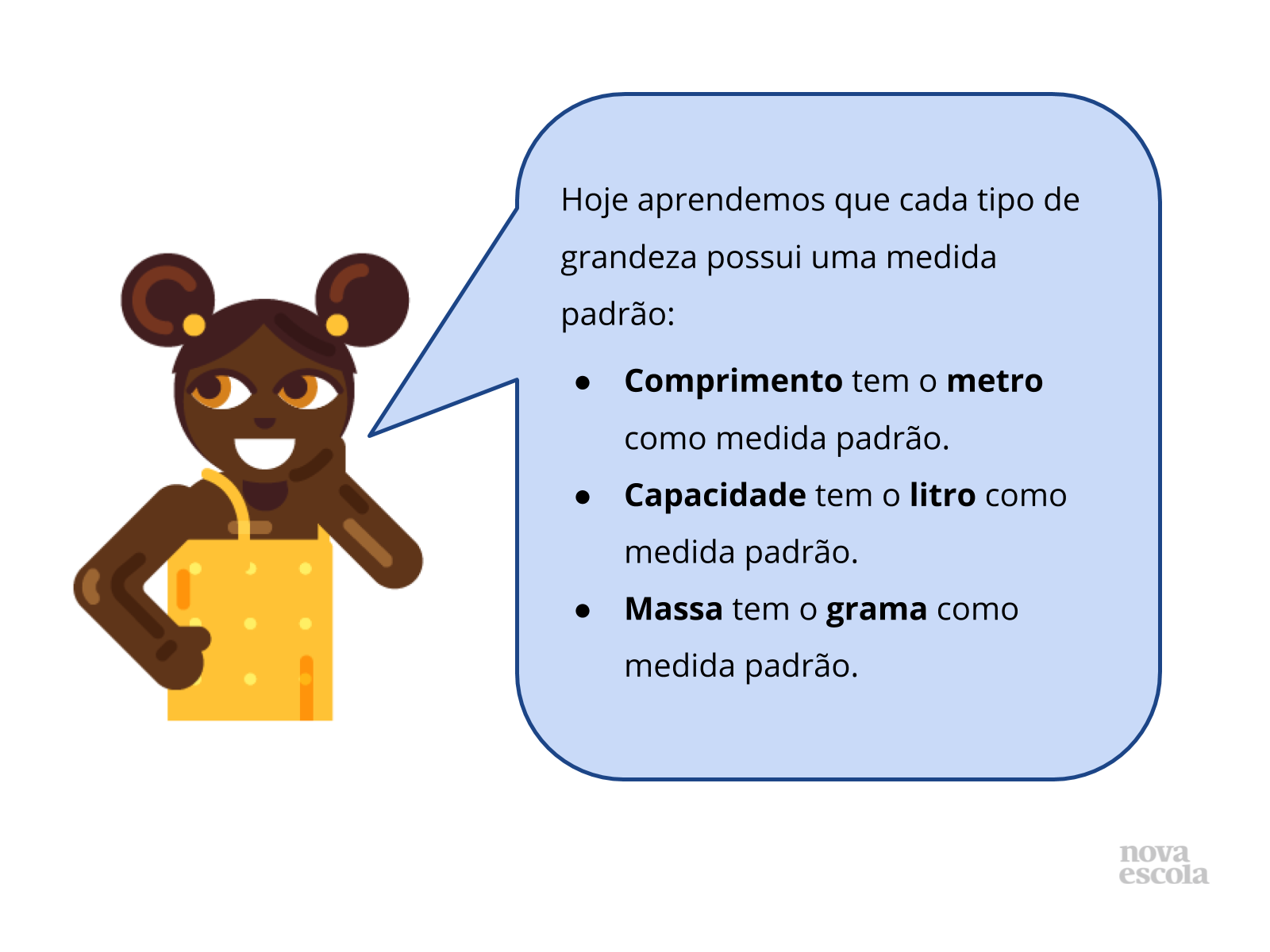
Orientações: A aula deve ser concluída com a retomada dos principais conhecimentos pretendidos: destaque as unidades de medida padrão referentes a cada grandeza e a necessidade de ter que dividi-las em partes menores para medir com precisão objetos muito pequenos, mais leves ou com menor quantidade que a medida padrão.
Propósito: Concluir a aula resumindo os conhecimentos produzidos.
Encerramento

Tempo sugerido: 3 minutos.
Orientações: A aula deve ser concluída com a retomada dos principais conhecimentos pretendidos: destaque as unidades de medida padrão referentes a cada grandeza e a necessidade de ter que dividi-las em partes menores para medir com precisão objetos muito pequenos, mais leves ou com menor quantidade que a medida padrão.
Propósito: Concluir a aula resumindo os conhecimentos produzidos.
Raio X

Tempo sugerido: 5 minutos.
Orientações: A intenção é que os alunos reflitam individualmente sobre a medida correta a ser utilizada na situação apresentada. Inicialmente, é interessante que os alunos leiam a questão sem o auxílio do professor, de modo que possam interpretar a situação e solucionar o problema. Utilize esse momento como forma de avaliar os alunos em termos de independência, formas diversas de pensar sobre o problema e alcance dos objetivos pretendidos na aula. Circule para verificar como os alunos estão pensando e registrando suas respostas. Você pode fazer o download desta atividade para imprimir para os seus alunos aqui.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante. Acesse aqui a resolução dessa atividade.
Materiais complementares para impressão:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 
























