Atividade Principal
Plano de Aula
Plano de aula: Ângulos em polígonos - construindo mosaicos e ladrilhamentos
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Ângulos em polígonos
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Rosilaine Sanches Martins
Mentor: Fabrício Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
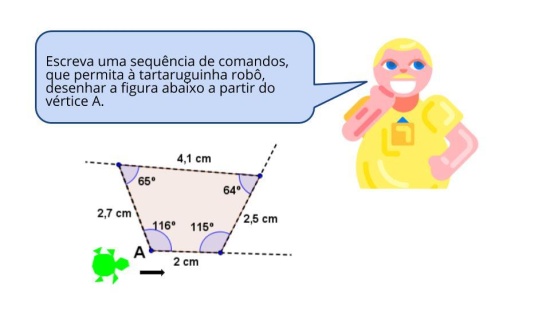
(EF07MA22) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos, à confecção de ferramentas e peças mecânicas, entre outras.
Objetivos específicos
Estabelecer relações entre ângulos internos de polígonos regulares na construção de mosaicos e ladrilhamentos.
Conceito-chave
Ângulos internos de polígonos regulares.
Recursos necessários
- Polígonos impressos em folhas;
- Atividades impressas em folhas, coladas no caderno ou não;
- Tesoura;
- Cola;
- Folhas de papel sulfite colorido ou cartolina colorida.
- Folhas de cartolina ou de papel sulfite brancas.
Habilidades BNCC:
Objetivos de aprendizagem
Estabelecer relações entre ângulos internos de polígonos regulares na construção de mosaicos e ladrilhamentos.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Novo curso gratuito

Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO