Resumo da Aula
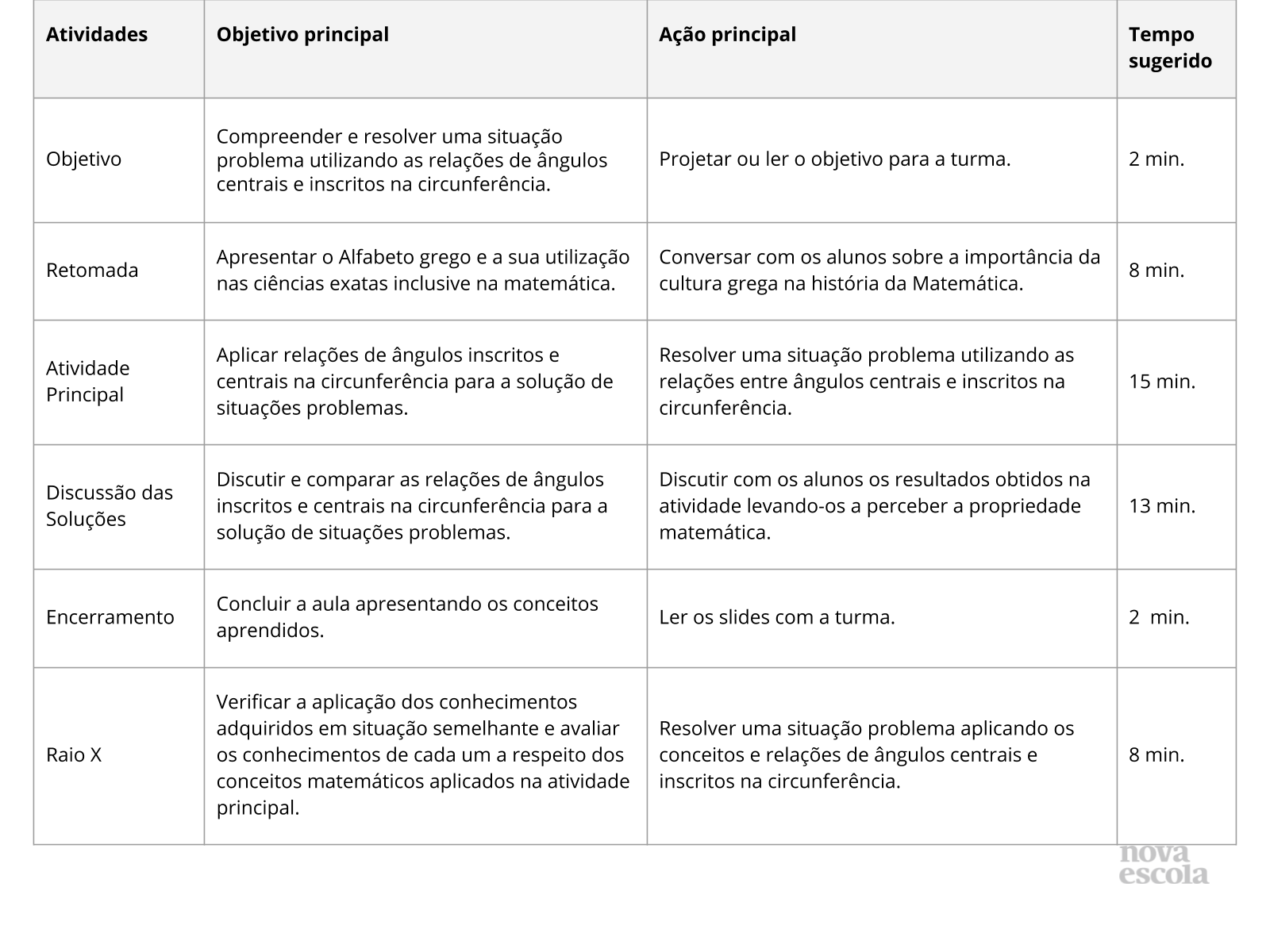
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Apresentar o objetivo para que fique claro o que se deseja atingir com essa aula.
Retomada

Tempo sugerido: 8 minutos. (slides 3, 4 e 5).
Orientações:
Distribua entre os alunos a atividade impressa e peça que leiam os nomes das letras gregas, peça aos alunos que levantem semelhanças e diferenças com o nosso alfabeto, como quantidade de letras e formato das letras.
Converse sobre a importância da cultura grega para a história da matemática e do conhecimento matemático, levante algumas contribuições da matemática grega e sua relevância até os dias de hoje.
Propósito: Apresentar o Alfabeto grego e a sua utilização nas ciências exatas inclusive na matemática.
Materiais complementares para impressão:
Aquecimento
Retomada

Tempo sugerido: 8 minutos. (slides 3, 4 e 5).
Orientações:
Distribua entre os alunos a atividade impressa e peça que leiam os nomes das letras gregas, peça aos alunos que levantem semelhanças e diferenças com o nosso alfabeto, como quantidade de letras e formato das letras.
Converse sobre a importância da cultura grega para a história da matemática e do conhecimento matemático, levante algumas contribuições da matemática grega e sua relevância até os dias de hoje.
Propósito: Apresentar o Alfabeto grego e a sua utilização nas ciências exatas inclusive na matemática.
Retomada
Tempo sugerido: 8 minutos. (slides 3, 4 e 5).
Orientações:
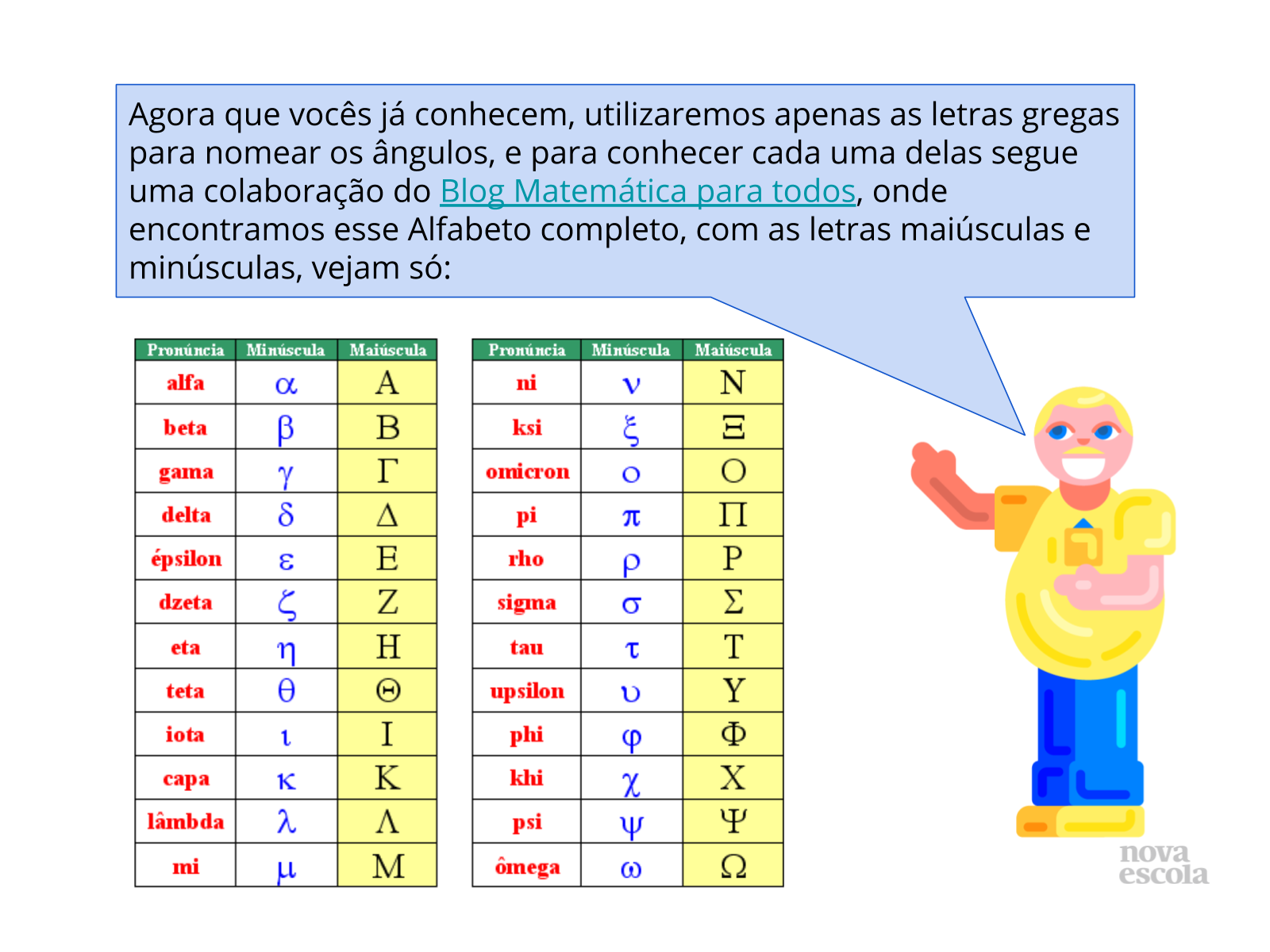
Distribua entre os alunos a atividade impressa e peça que leiam os nomes das letras gregas, peça aos alunos que levantem semelhanças e diferenças com o nosso alfabeto, como quantidade de letras e formato das letras.
Converse sobre a importância da cultura grega para a história da matemática e do conhecimento matemático, levante algumas contribuições da matemática grega e sua relevância até os dias de hoje.
Propósito: Apresentar o Alfabeto grego e a sua utilização nas ciências exatas inclusive na matemática.
Atividade principal

Tempo sugerido: 15 minutos. (slide 6 e 7).
Orientações:
Desafie seus alunos a desenvolverem a solução do problema de forma individual, ressalte a utilização das letras gregas para representar os ângulos nesta atividade.
Converse com os alunos sobre a importância da geometria para a construção civil, desperte o interesse da turma para realizar a atividade como um esboço de uma construção. Levante com os alunos outras situações cotidianas onde a geometria é fundamental.
Propósito: Aplicar relações de ângulos inscritos e centrais na circunferência para a solução de situações-problema.
Discuta com a turma:
- O que precisamos para construir uma circunferência?
- Como saber que um arco possui 120º?
- É possível que os desenhos fiquem em posições diferentes?
- A posição do triângulo influência na resolução do problema?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Imagens para o Guia de Intervenção
Atividade principal
Tempo sugerido: 15 minutos. (slide 6 e 7).
Orientações:
Desafie seus alunos a desenvolverem a solução do problema de forma individual, ressalte a utilização das letras gregas para representar os ângulos nesta atividade.
Converse com os alunos sobre a importância da geometria para a construção civil, desperte o interesse da turma para realizar a atividade como um esboço de uma construção. Levante com os alunos outras situações cotidianas onde a geometria é fundamental.
Propósito: Aplicar relações de ângulos inscritos e centrais na circunferência para a solução de situações-problema.
Discuta com a turma:
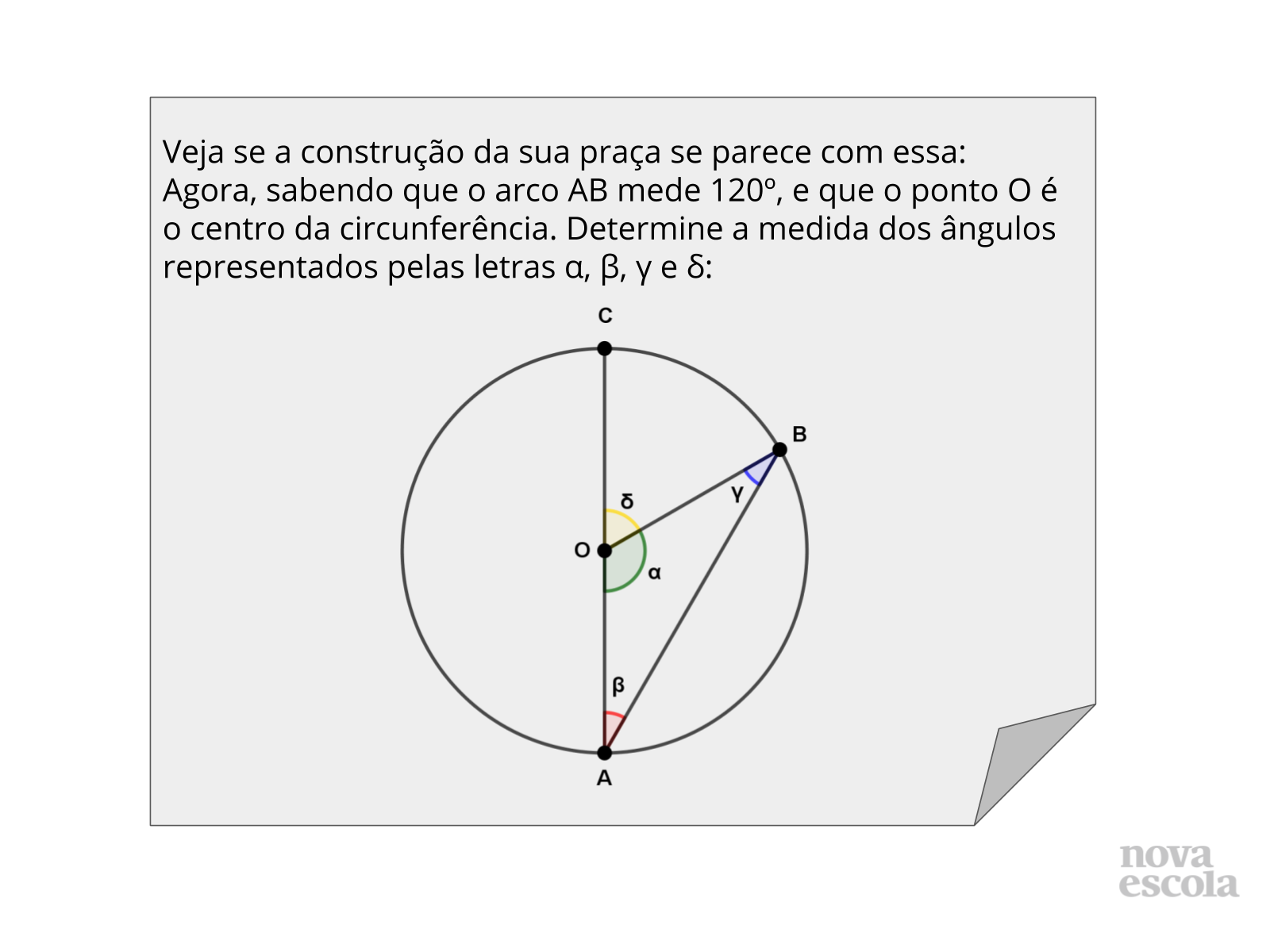
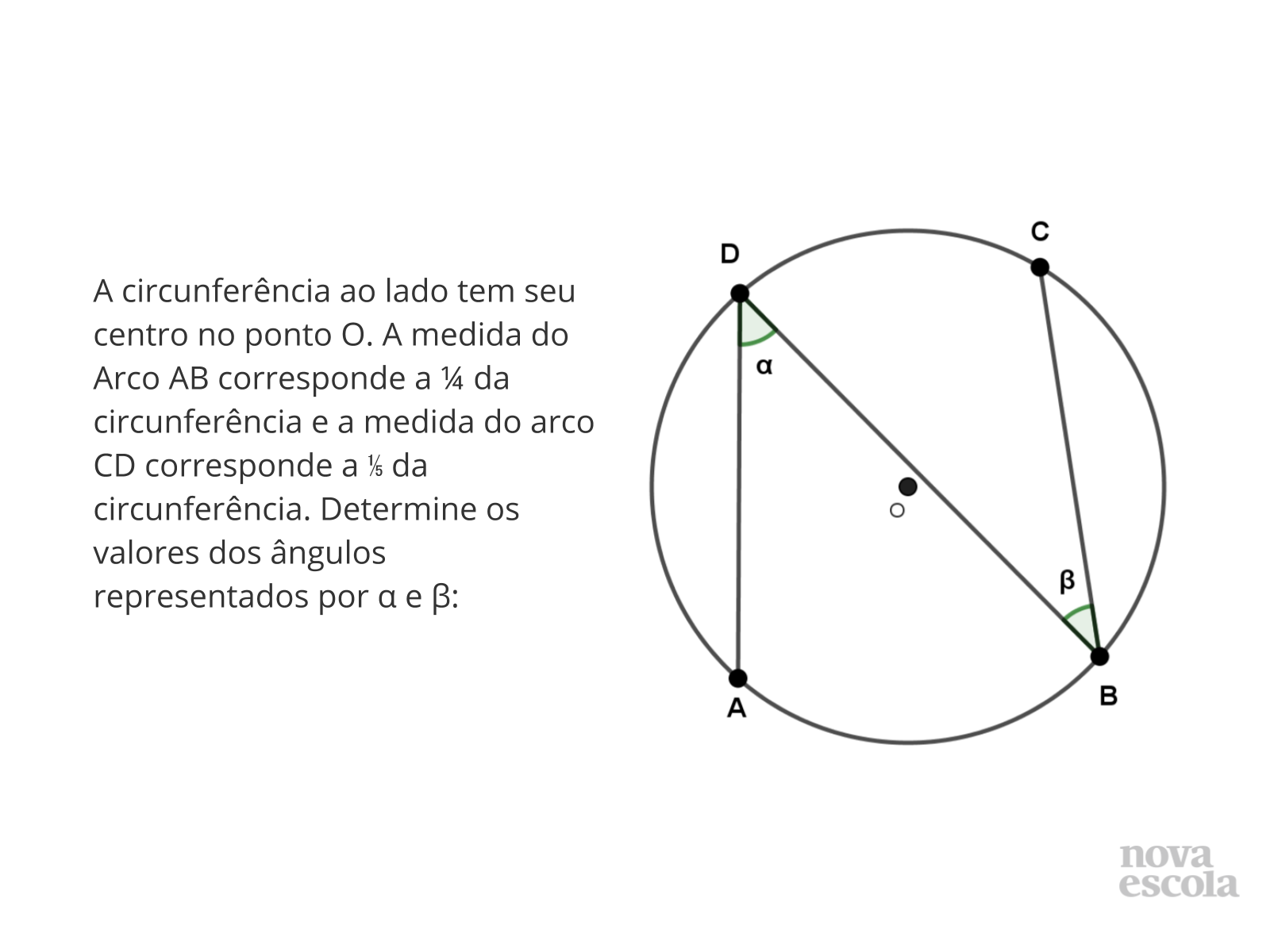
- É possível encontrar ângulos centrais e inscritos nessa circunferência?
- Que outros arcos estão representados na imagem além do arco AB citado no enunciado?
- Que relações podemos estabelecer entre os ângulos?
- Há outras formas de solucionar o problema?
- Por que a informação que O é o centro da circunferência é necessária? Seria possível resolver o problema sem essa informação?
- O que precisamos saber para solucionar este problema (estimule os alunos a relembrarem a propriedade da soma dos ângulos internos de um triângulos e o que são ângulos suplementares, adjacentes e opostos pelo vértice.)
Atividade Principal
Tempo sugerido: 13 minutos. (slides 8 a 13).
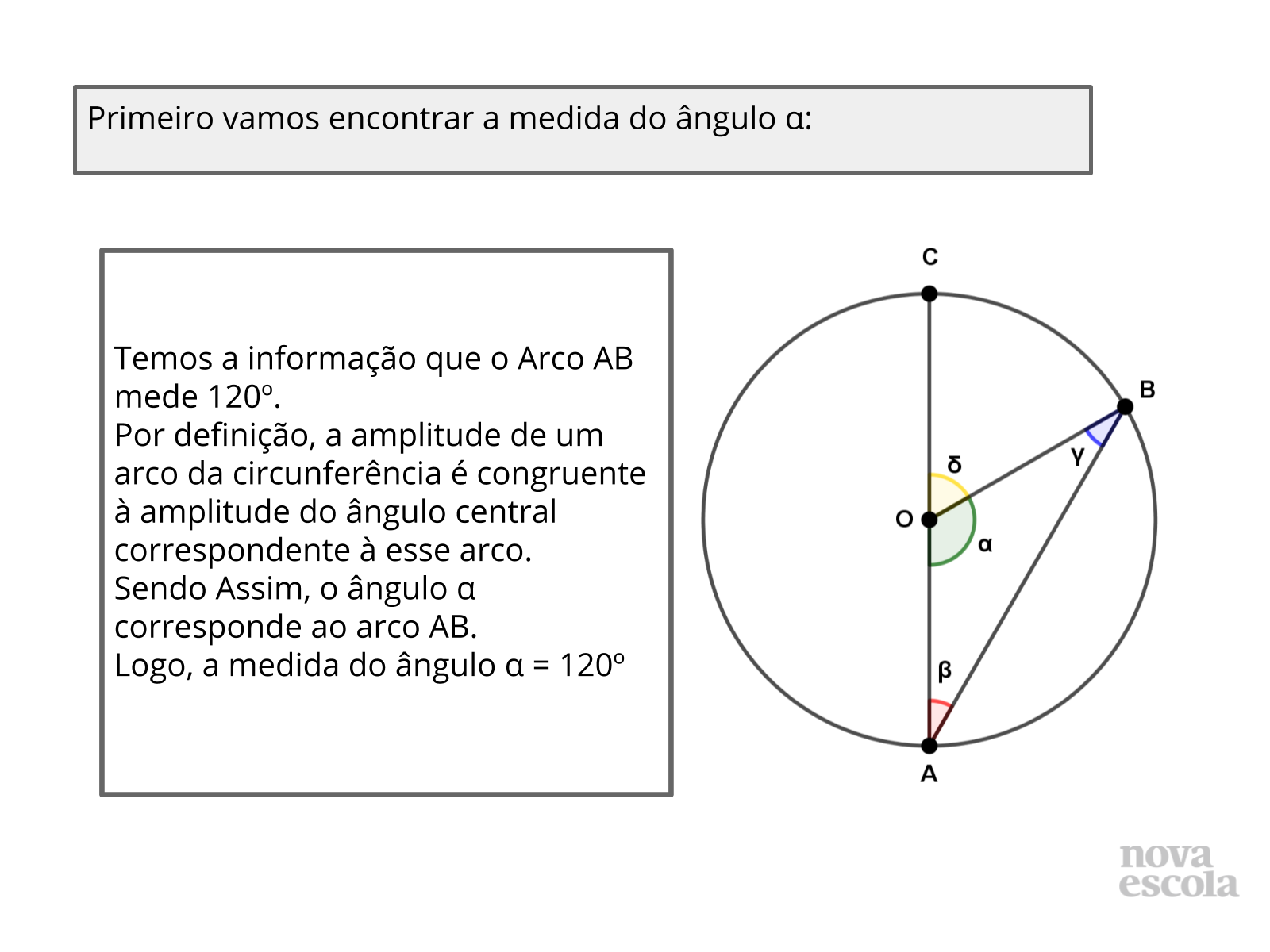
Orientações: Convide 2 a três alunos e peça que compartilhem no quadro a solução que utilizaram para encontrar a medida do ângulo ?. Pergunte a turma se alguém solucionou o problema de outra forma e peça que compartilhe no quadro com os colegas.
Propósito: Discutir e comparar as relações de ângulos inscritos e centrais na circunferência para a solução de situações problemas.
Discuta com a turma:
- Todos começaram resolvendo a medida do ângulo ??
- Com as informações que temos, é possível iniciar a solução deste problema encontrando a medida de outro ângulo?
- Que informações do problema são importantes para que possamos encontrar a medida do ângulo ??
- Que conhecimentos aplicamos na resolução deste item?
Atividade Principal
Tempo sugerido: 13 minutos. (slides 8 a 13).
Orientações: Convide 2 a três alunos e peça que que compartilhem no quadro a solução que utilizaram para encontrar a medida do ângulo ?. Pergunte a turma se alguém solucionou o problema de outra forma e peça que compartilhe no quadro com os colegas.
Propósito: Discutir e comparar as relações de ângulos inscritos e centrais na circunferência para a solução de situações problemas.
Discuta com a turma:
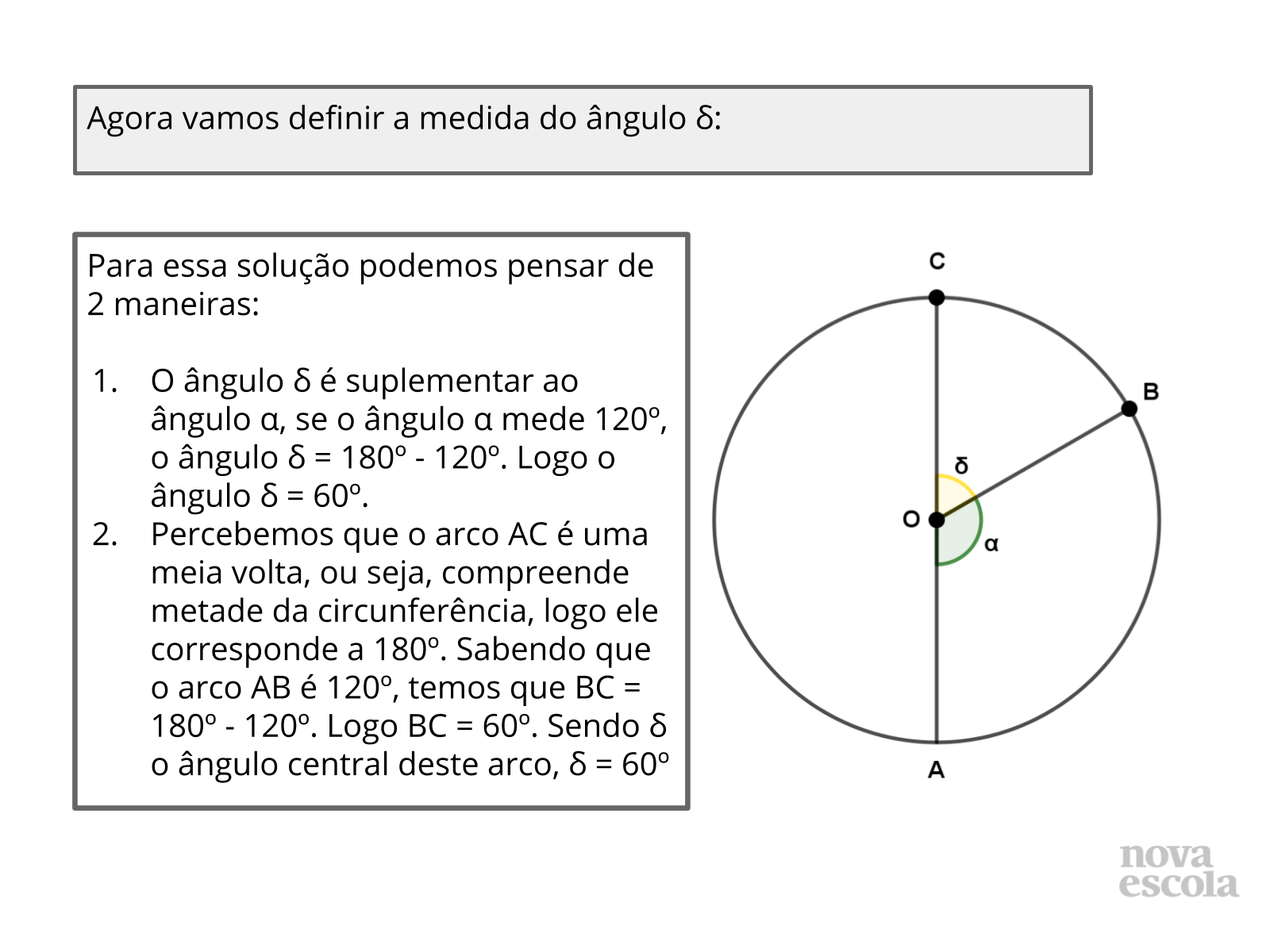
- Além das duas soluções apresentadas, existem outras maneiras de solucionar este problema?
- O que são ângulos suplementares?
- Por que podemos afirmar que a soma dos ângulos ? e ? é 180º?
- Se o ponto C não estivesse indicado, seria possível solucionar o problema como proposto na solução 2?
Atividade Principal
Tempo sugerido: 13 minutos. (slides 8 a 13).
Orientações: Convide 2 a três alunos e peça que que compartilhem no quadro a solução que utilizaram para encontrar a medida do ângulo ?. Pergunte a turma se alguém solucionou o problema de outra forma e peça que compartilhe no quadro com os colegas.
Propósito: Discutir e comparar as relações de ângulos inscritos e centrais na circunferência para a solução de situações problemas.
Discuta com a turma:
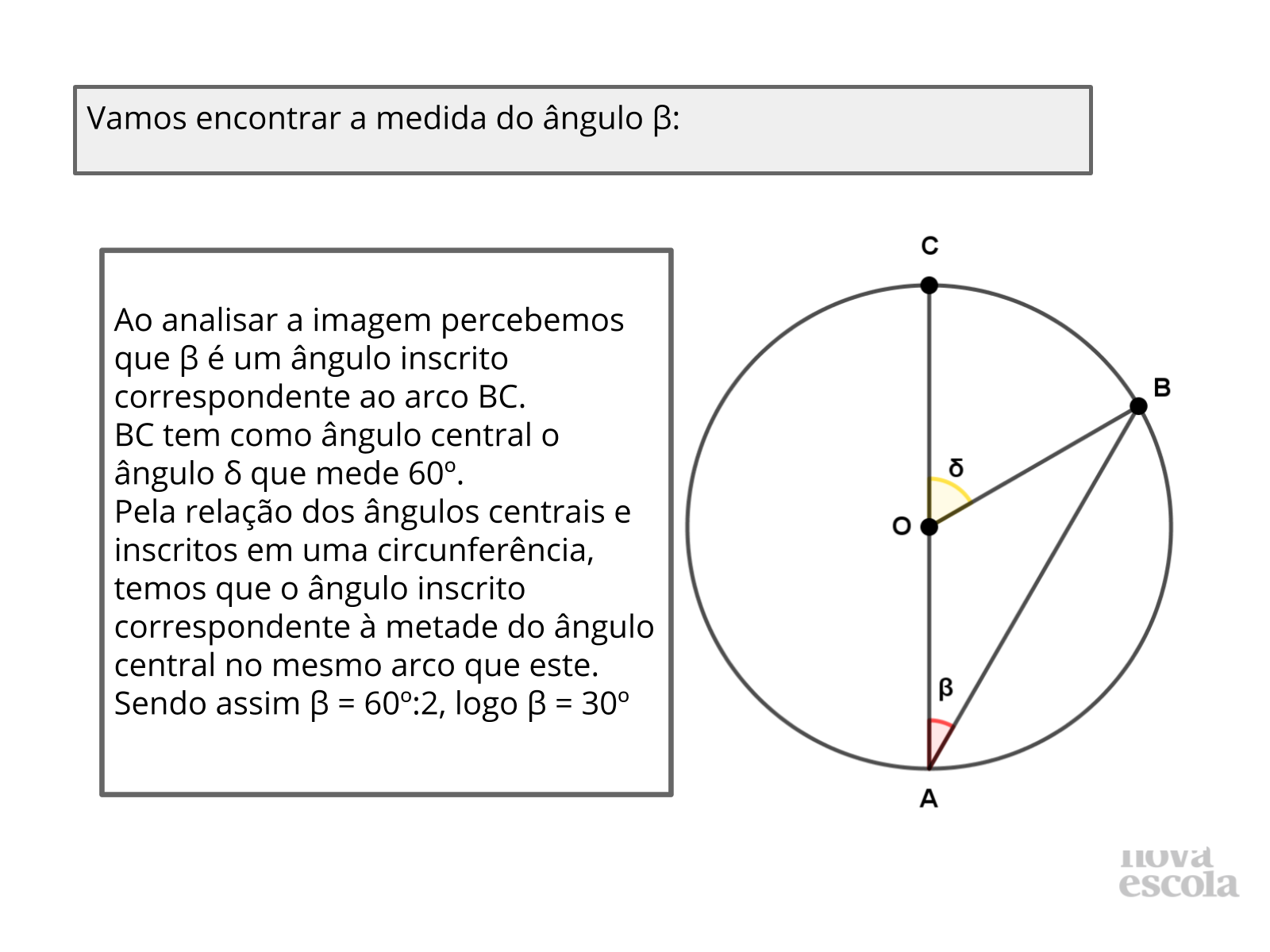
- Além da solução apresentada, existem outras maneiras de solucionar este problema?
- O que é um ângulo central?
- O que é um ângulo inscrito?
- De que forma as definições de ângulos centrais e inscritos auxiliam na solução deste ângulo?
Atividade Principal
Tempo sugerido: 13 minutos. (slides 8 a 13).
Orientações: Convide 2 a três alunos e peça que que compartilhem no quadro a solução que utilizaram para encontrar a medida do ângulo ?. Pergunte a turma se alguém solucionou o problema de outra forma e peça que compartilhe no quadro com os colegas.
Propósito: Discutir e comparar as relações de ângulos inscritos e centrais na circunferência para a solução de situações problemas.
Discuta com a turma:
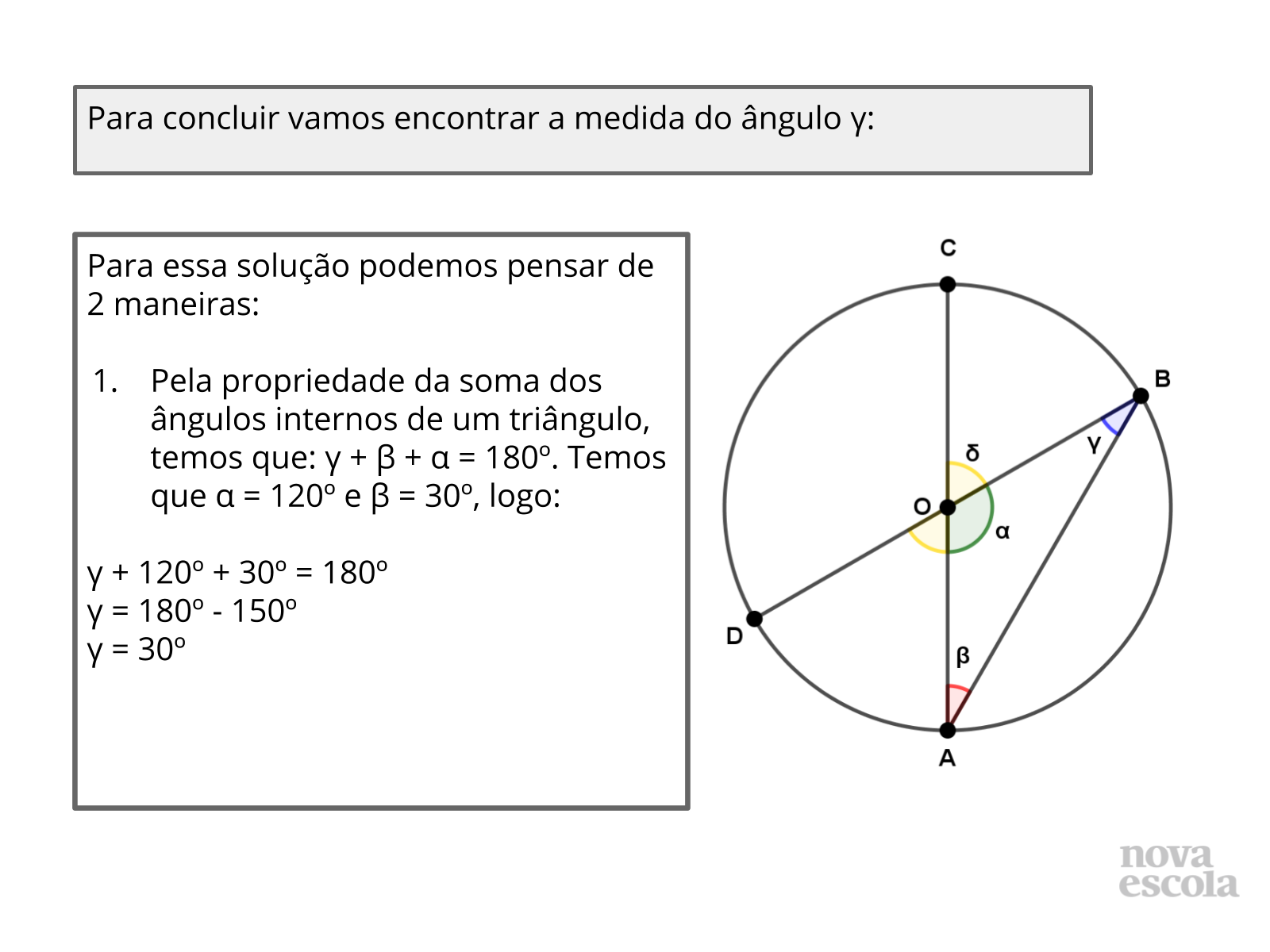
- Além da solução apresentada, existem outras maneiras de solucionar este problema?
- A propriedade da soma dos ângulos internos de um triângulo é válida para qualquer triângulo?
Atividade Principal
Tempo sugerido: 13 minutos. (slides 8 a 13).
Orientações: Convide 2 a três alunos e peça que que compartilhem no quadro a solução que utilizaram para encontrar a medida do ângulo ?. Pergunte a turma se alguém solucionou o problema de outra forma e peça que compartilhe no quadro com os colegas.
Propósito: Discutir e comparar as relações de ângulos inscritos e centrais na circunferência para a solução de situações problemas.
Discuta com a turma:
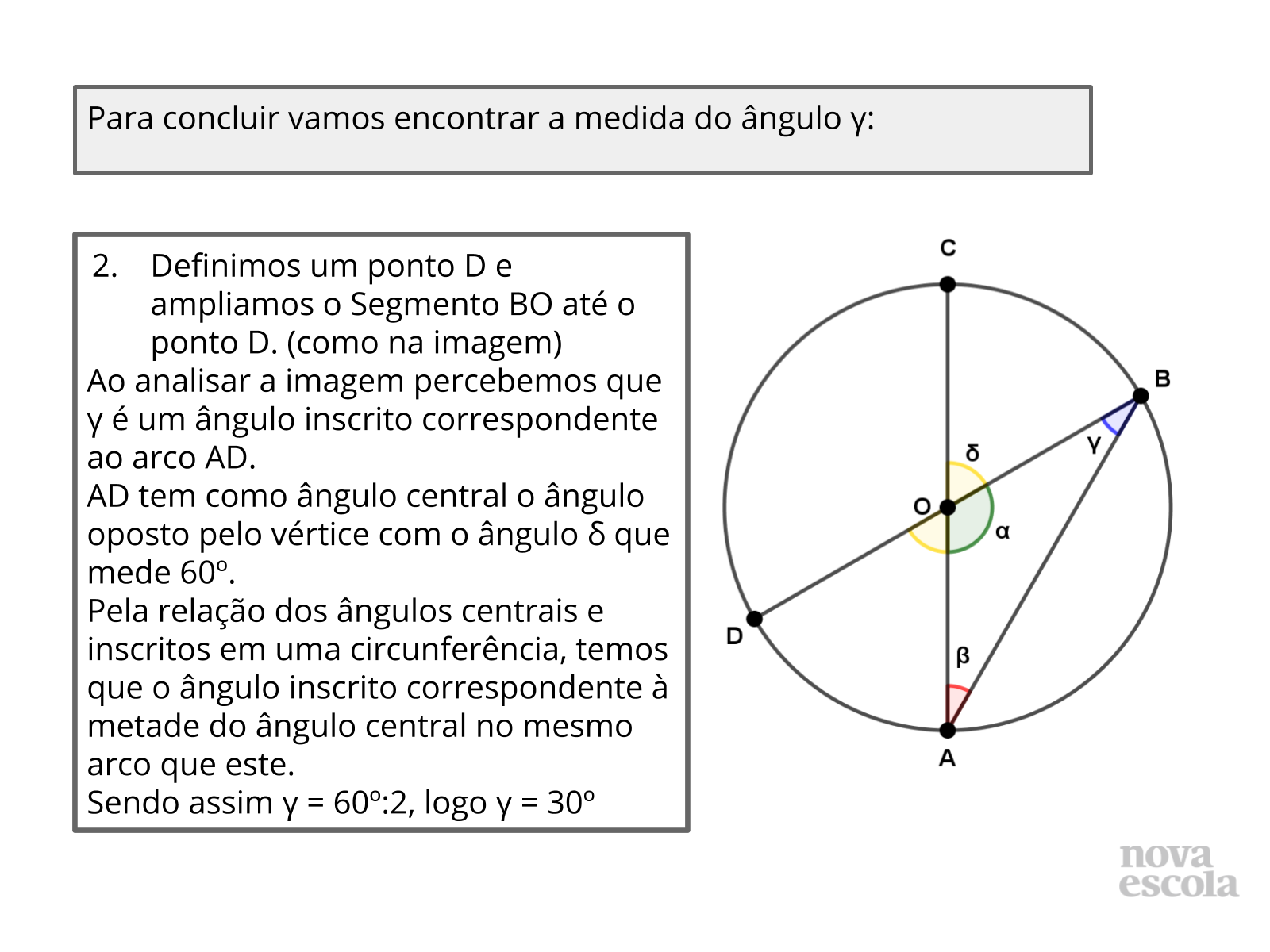
- Além da solução apresentada, existem outras maneiras de solucionar este problema?
- O ponto D pode ser colocado em qualquer posição na circunferência para solucionar este problema?
- Que relação usamos para prolongar o segmento BO?
- Se não tivéssemos a informação que o ponto O é o centro da circunferência, seria possível resolver dessa forma?
Atividade Principal
Tempo sugerido: 13 minutos. (slides 8 a 13).
Orientações: Convide 2 a três alunos e peça que que compartilhem no quadro a solução que utilizaram para encontrar a medida do ângulo ?. Pergunte a turma se alguém solucionou o problema de outra forma e peça que compartilhe no quadro com os colegas.
Propósito: Discutir e comparar as relações de ângulos inscritos e centrais na circunferência para a solução de situações problemas.
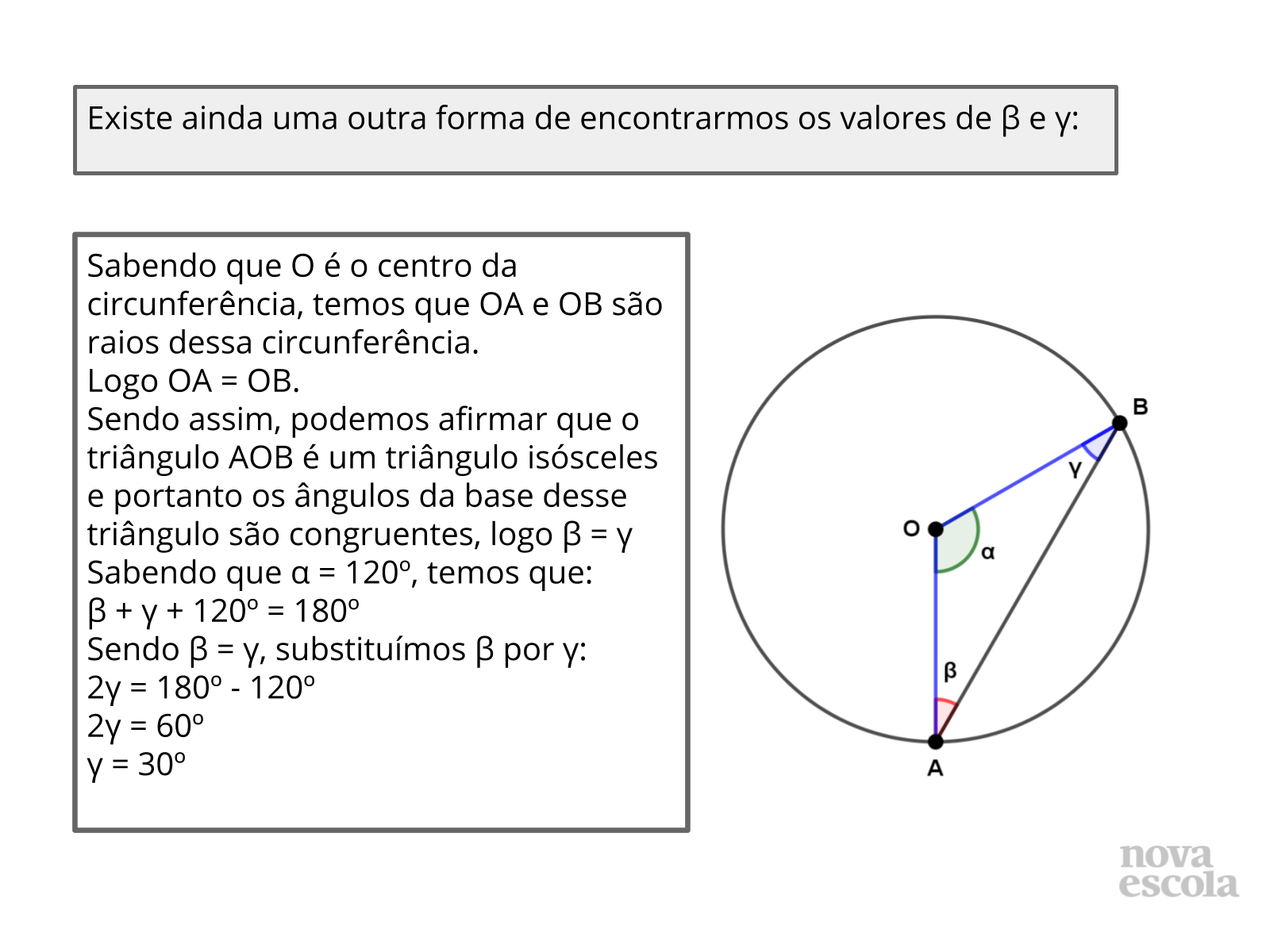
Discuta com a turma:
- O que é um triângulo isósceles?
- Porque podemos afirmar que os ângulos da base de um triângulo isósceles são iguais?
- Se não utilizássemos a soma dos ângulos internos do triângulo, teria outra forma de resolver este item pensando no triângulo isósceles? (espera-se se que os alunos indiquem a solução pelo ângulo externo)
Atividade Principal

Tempo sugerido: 1 minuto.
Orientações: Leia com os alunos as afirmações do slide e solicite que registrem em seus cadernos as definições apresentadas.
Propósito: Concluir a aula apresentação os conceitos aprendidos.
Raio X
Tempo sugerido: 8 minutos.
Orientações:
Solicite que leiam a atividade e a realizem individualmente. Circule para verificar como os alunos estão realizando a atividade e se ainda possuem dúvidas. É importante que os alunos percebam que só é possível solucionar a questão porque temos a informação que é um polígono regular de oito lados iguais. Portanto, terá 8 ângulos iguais e 8 ângulos centrais iguais.
Propósito: Verificar se os alunos conseguem aplicar os conhecimentos adquiridos ao longo dessa aula.
Discuta com a turma:
- Como podemos classificar esses ângulos em relação à sua posição na circunferência?
- É possível encontrar ângulos centrais correspondentes a esses ângulos?
- Existe outra forma de determinar a medida desses ângulos?
- Como a medida do arco nos ajuda a solucionar este problema?
Materiais complementares para impressão:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar
Cartazes propriedades de ângulos
Classificação dos triângulos
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 























