Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.”
Objetivo

Tempo sugerido: 2 min
Orientação: Apresente o objetivo, através da leitura, escrita no quadro ou projeção do mesmo.
Propósito: Compartilhar o objetivo de aprendizagem com a turma.
Orientações para o desenvolvimento da aula:
Objetivo: Calcular porcentagem de uma quantidade sem uso da regra de três.
Deve-se ter como foco a construção do conhecimento de forma que os estudantes concluam, através da atividade principal, generalizações do cálculo da porcentagem de uma quantidade.
Também é importante manter o vocabulário matemático, como por exemplo:
- Porcentagem de.
- Fração centesimal equivalente.
- Número decimal equivalente.
Discuta com a turma:
- Como calcular a porcentagem de uma quantidade?
Adequações:
- Caso seja possível, pode-se fazer o trabalho com o uso da calculadora para encontrar a porcentagem de uma quantidade.
- Caso não seja possível a impressão das atividades pode-se passar no quadro.
- Para estudantes com problemas de visão (baixa visão) pode-se solicitar material ampliado, ou escrever em cartolina, em uma escala grande o enunciado.
- Para estudantes com outras especificidades pode-se alterar as variáveis postas nos itens para valores menores, mediando o cálculo da porcentagem.
Material complementar:
- Vídeo que apresenta como calcular acréscimo ou desconto, com uso de calculadora. Para acessar o vídeo, clique aqui.
Atividade de aquecimento

Tempo sugerido: 5 min
Orientação: Entregar a atividade para os estudantes e observar se retomam o conteúdo de cálculo de frações de uma quantidade.
Agrupe os alunos em duplas e peça para que resolvam o que está sendo pedido, utilizando a estratégia que desejar.
Para imprimir a atividade clique aqui.
Para visualizar a resolução clique aqui.
Propósito: Relembrar o conceito de frações de uma quantidade.
Discuta com a turma:
- Relembre sobre o conceito de fração e como se deve efetuar o cálculo da fração de uma quantidade.
Possível soluções:
Alguns amigos foram jantar fora e resolveram dividir o valor da conta em partes iguais.
- Sabendo que a conta ficou em R$ 400,00 e que cada amigo pagou um quinto desse valor, calcule quanto cada um pagou.
Resolução:
Basta dividir o valor por 5 (um quinto) e em seguida multiplicar por 1.
400 : 5 = 80 ? 80 x 1 = 80
Logo, cada amigo vai pagar R$ 80,00.
- Sabendo que a conta ficou em R$ 300,00 e que cada amigo pagou um terço desse valor, calcule quanto cada um pagou.
Resolução:
Basta dividir o valor por 3 (um terço) e em seguida multiplicar por 1.
300 : 3 = 100 ? 100 x 1 = 100
Logo, cada amigo vai pagar R$ 100,00.
Materiais complementares:
Atividade aquecimento
Resolução atividade aquecimento
Atividade Principal
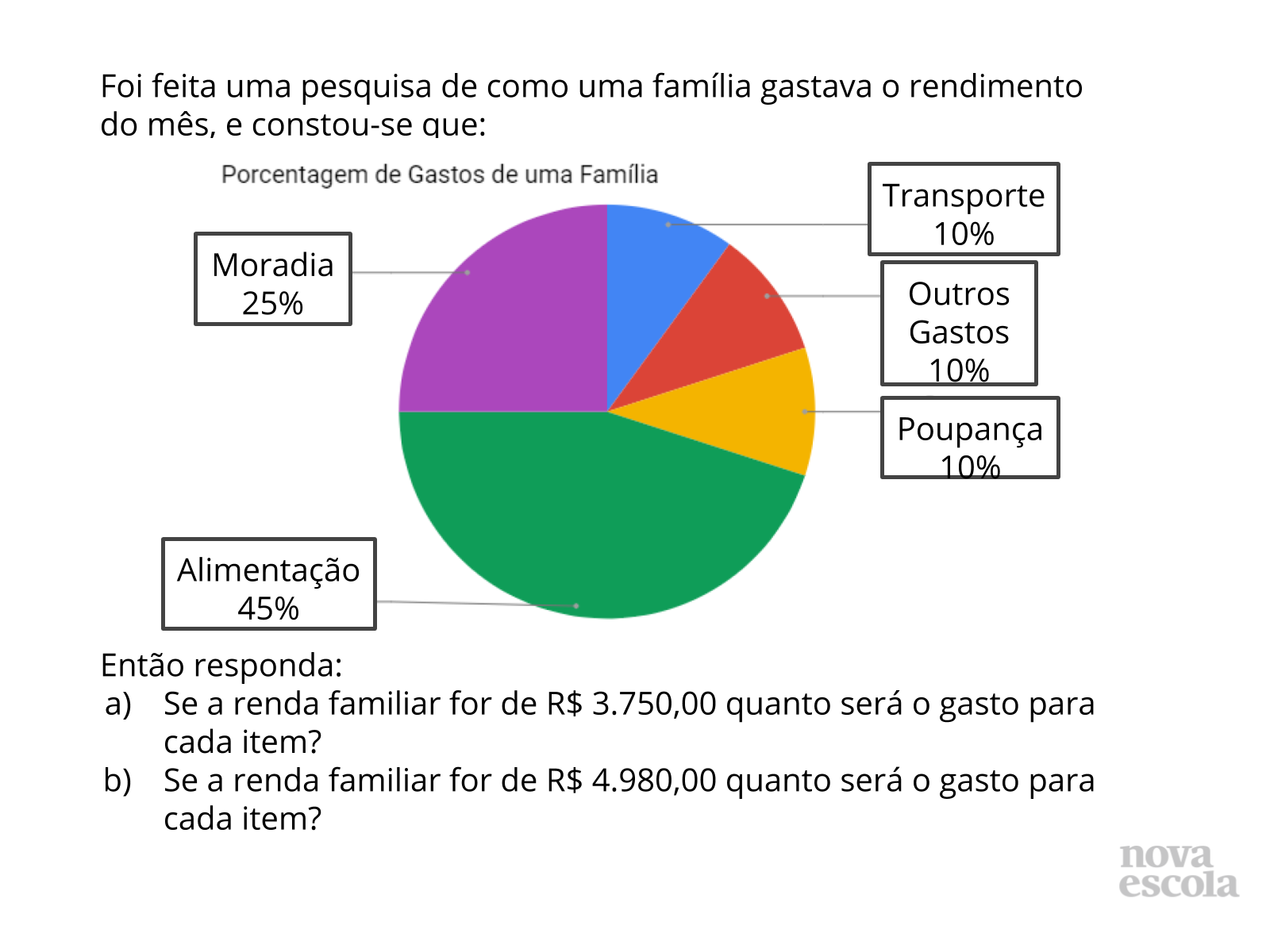
Tempo sugerido: 15 min
Orientação:
1º momento: peça que, individualmente, leiam e realizem a atividade - 4 minutos
Para esse momento, observe as respostas encontradas individualmente para que em seguida, divida a turma de forma que fiquem juntos os estudantes que obtiveram respostas diferentes.
2º momento: peça que em duplas, comparem as respostas encontradas e formulem uma resposta da dupla - 7 minutos
Esse é um momento muito importante, pois com a separação planejada das duplas, a discussão deverá ser mediada pelo professor, para que os estudantes troquem e argumentem sobre a sua estratégia de resolução.
3º momento: as duplas deverão compartilhar, em um debate coletivo, suas estratégias e respostas - 4 minutos
Você pode fazer o download desta atividade para imprimir para seus alunos aqui.
Para imprimir as possíveis soluções clique aqui.
Utilize o guia de intervenção para discutir com os alunos as estratégias de cálculo de porcentagem.
Propósito: Resolver a atividade sugerida
Materiais complementares:
Atividade principal
Resolução atividade principal
Guia de intervenção
Discussão de Soluções
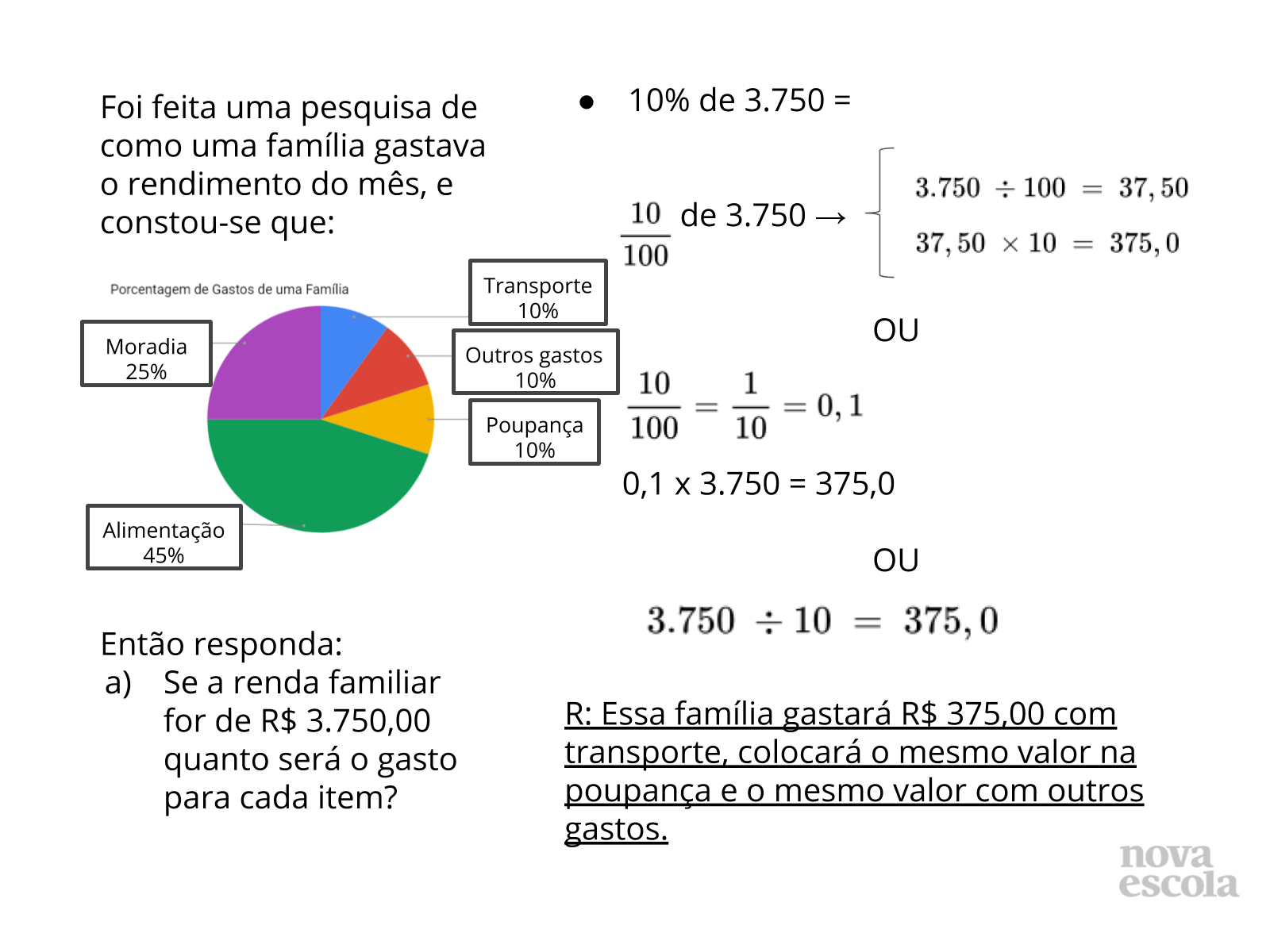
Tempo sugerido: 15 min (slides 5 a 10).
Orientação:
Após compartilhar as estratégias de resolução apresentadas pelos alunos, apresente esta sequência de slides, como forma de organizar as diversas formas de resolver a atividade proposta.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
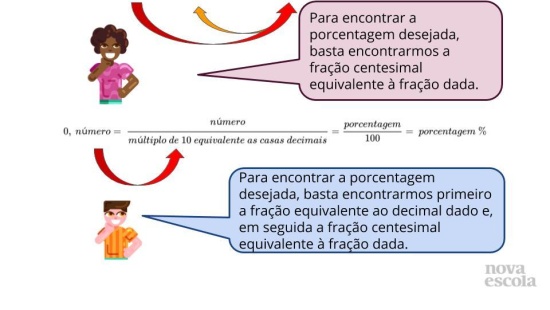
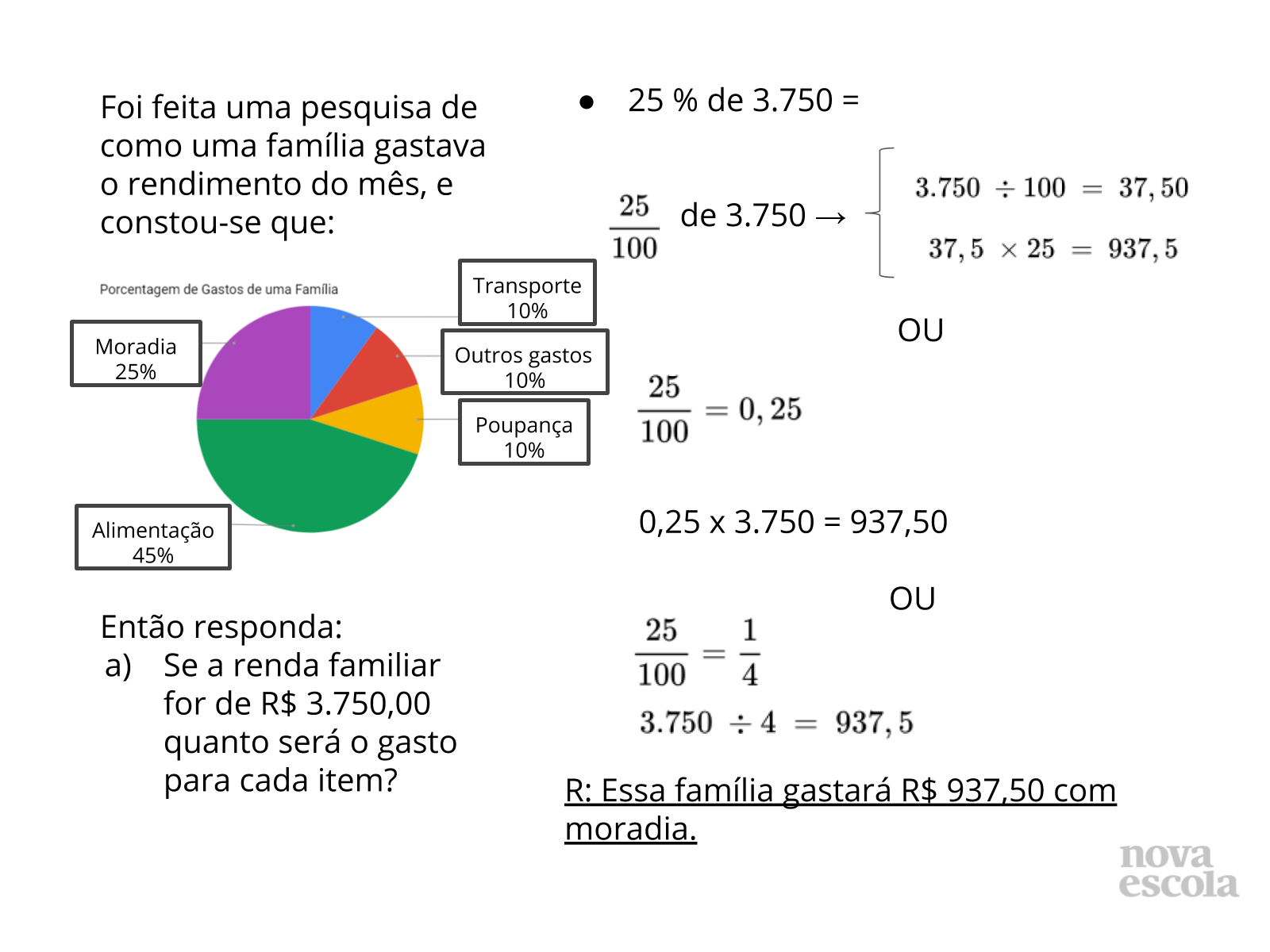
- Qual a relação que existe entre a fração centesimal e o número decimal que é multiplicado pela quantidade dada?
- Existem outras formas de resolver?
- Aproveite para questionar sobre as diferenças entre as quantidades de resoluções, dependendo da porcentagem.
- Por exemplo: 10% tem uma fração equivalente diferente da centesimal, e 45% não. Por que isso acontece?
Discussão de Soluções
Tempo sugerido: 15 min (slides 5 a 10).
Orientação:
Após compartilhar as estratégias de resolução apresentadas pelos alunos, apresente esta sequência de slides, como forma de organizar as diversas formas de resolver a atividade proposta.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
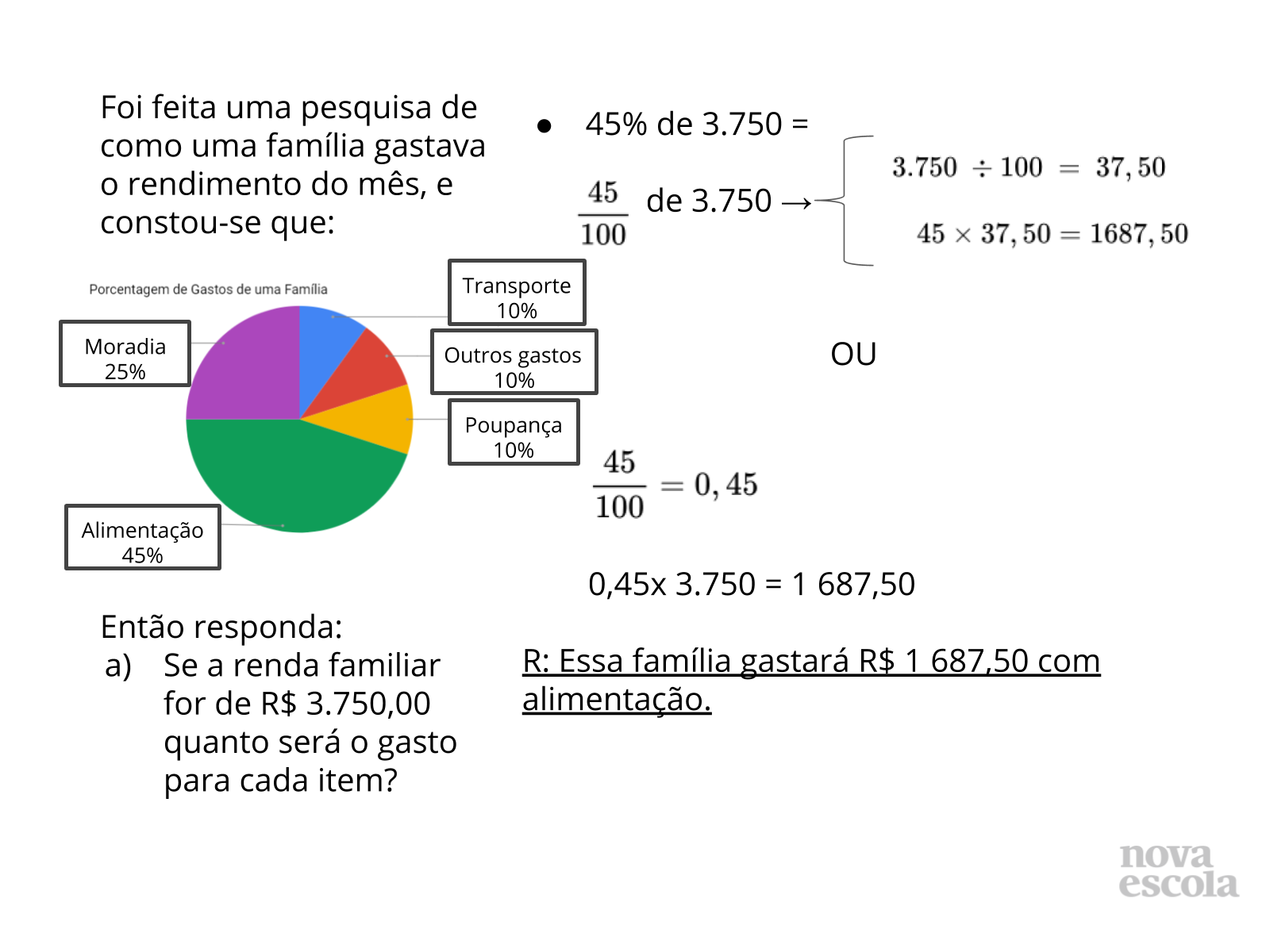
- Qual a relação que existe entre a fração centesimal e o número decimal que é multiplicado pela quantidade dada?
- Existem outras formas de resolver?
- Aproveite para questionar sobre as diferenças entre as quantidades de resoluções, dependendo da porcentagem.
- Por exemplo: 10% tem uma fração equivalente diferente da centesimal, e 45% não. Por que isso acontece?
Discussão de Soluções
Tempo sugerido: 15 min (slides 5 a 10).
Orientação:
Após compartilhar as estratégias de resolução apresentadas pelos alunos, apresente esta sequência de slides, como forma de organizar as diversas formas de resolver a atividade proposta.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
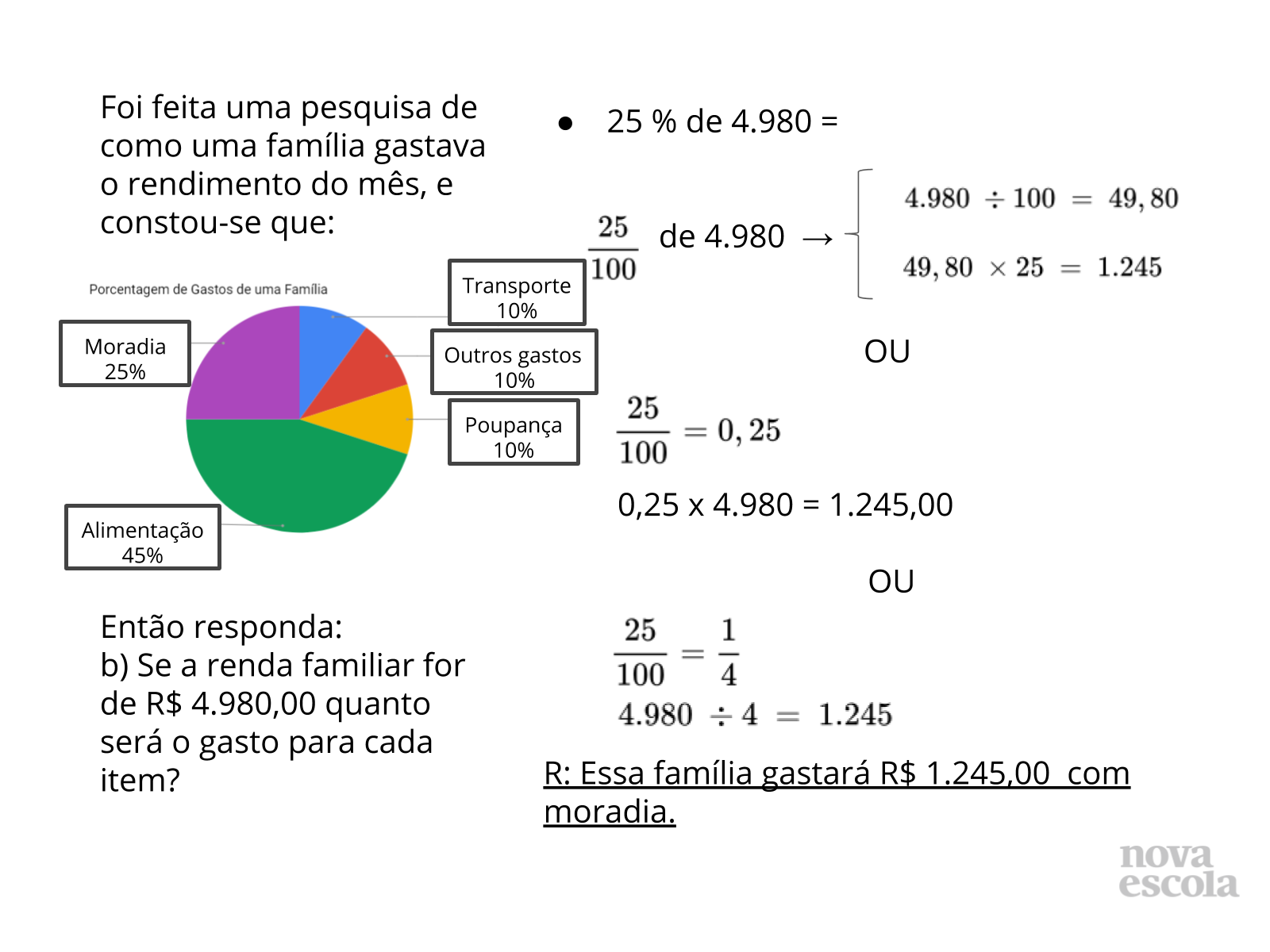
- Qual a relação que existe entre a fração centesimal e o número decimal que é multiplicado pela quantidade dada?
- Existem outras formas de resolver?
- Aproveite para questionar sobre as diferenças entre as quantidades de resoluções, dependendo da porcentagem.
- Por exemplo: 10% tem uma fração equivalente diferente da centesimal, e 45% não. Por que isso acontece?
Discussão de Soluções

Tempo sugerido: 15 min (slides 5 a 10).
Orientação:
Após compartilhar as estratégias de resolução apresentadas pelos alunos, apresente esta sequência de slides, como forma de organizar as diversas formas de resolver a atividade proposta.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
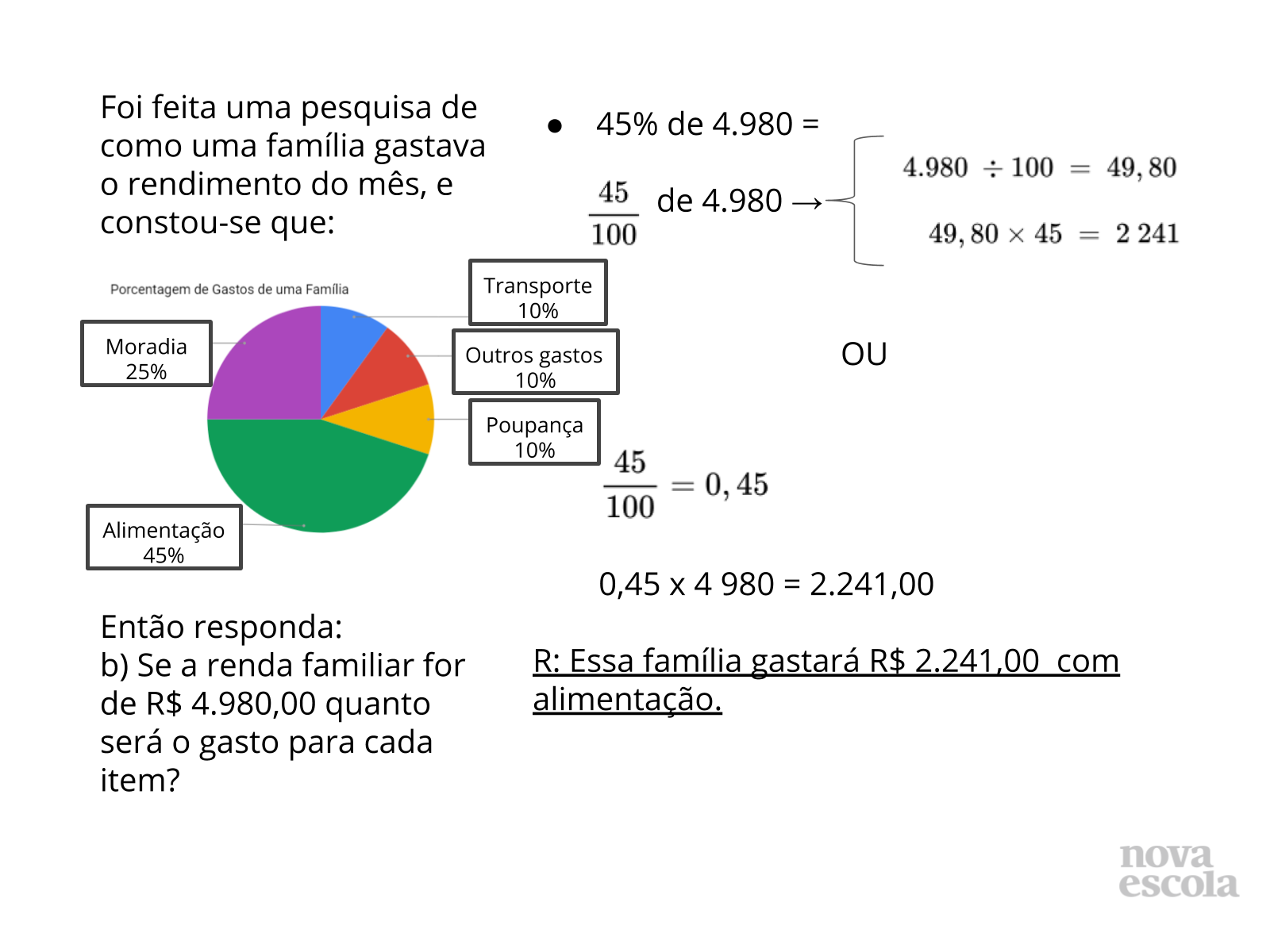
- Qual a relação que existe entre a fração centesimal e o número decimal que é multiplicado pela quantidade dada?
- Existem outras formas de resolver?
- Aproveite para questionar sobre as diferenças entre as quantidades de resoluções, dependendo da porcentagem.
- Por exemplo: 10% tem uma fração equivalente diferente da centesimal, e 45% não. Por que isso acontece?
Discussão de Soluções
Tempo sugerido: 15 min (slides 5 a 10).
Orientação:
Após compartilhar as estratégias de resolução apresentadas pelos alunos, apresente esta sequência de slides, como forma de organizar as diversas formas de resolver a atividade proposta.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
- Qual a relação que existe entre a fração centesimal e o número decimal que é multiplicado pela quantidade dada?
- Existem outras formas de resolver?
- Aproveite para questionar sobre as diferenças entre as quantidades de resoluções, dependendo da porcentagem.
- Por exemplo: 10% tem uma fração equivalente diferente da centesimal, e 45% não. Por que isso acontece?
Discussão de Soluções
Tempo sugerido: 15 min (slides 5 a 10).
Orientação:
Após compartilhar as estratégias de resolução apresentadas pelos alunos, apresente esta sequência de slides, como forma de organizar as diversas formas de resolver a atividade proposta.
Propósito: Compartilhar diferentes estratégias de resolução.
Discuta com a turma:
- Qual a relação que existe entre a fração centesimal e o número decimal que é multiplicado pela quantidade dada?
- Existem outras formas de resolver?
- Aproveite para questionar sobre as diferenças entre as quantidades de resoluções, dependendo da porcentagem.
- Por exemplo: 10% tem uma fração equivalente diferente da centesimal, e 45% não. Por que isso acontece?
Encerramento
Tempo sugerido: 5 minutos
Orientação: Encerre com os estudantes fazendo um resumo do que foi visto na aula e retomando o cálculo de porcentagem.
Propósito: Fazer o fechamento da aula e retomada da ferramenta de cálculo da porcentagem.
Discuta com a turma:
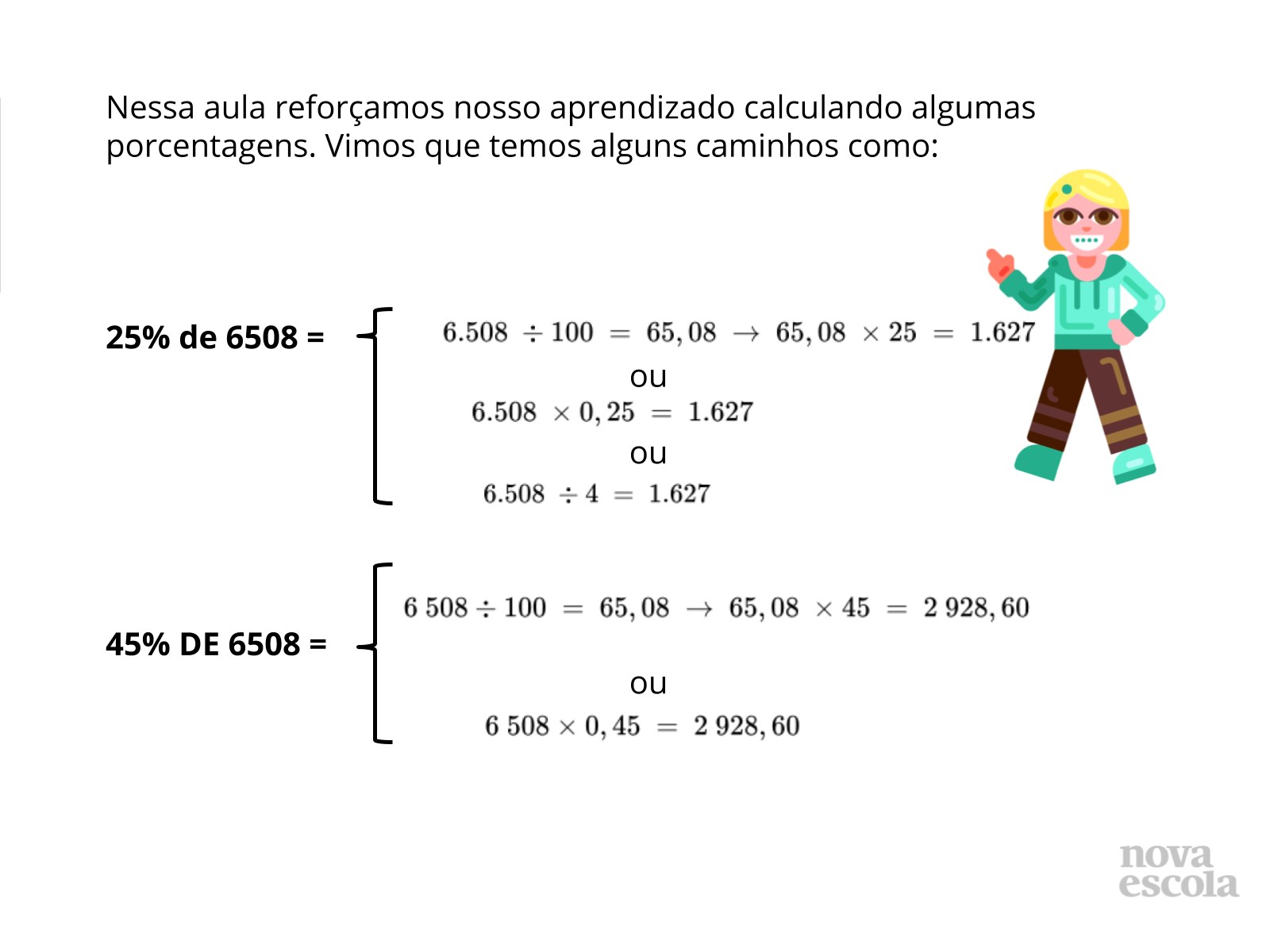
- Compare com os estudantes a relação entre as frações centesimais e os decimais equivalentes.
- Questione sobre a porcentagem 25% e 45%. Por que 45% não encontramos uma fração equivalente centesimal?
- Pergunte aos alunos se ficaram com alguma dúvida. O que aprenderam de novo? O que acharam da aula?
Raio X
Tempo sugerido: 8 min
Orientação: Peça para que, individualmente, calcule os valores com os acréscimos e com os descontos.
Propósito: Retomar as estratégias trabalhadas nessa unidade e verificar o conhecimento aprendido.
Para imprimir a atividade clique aqui.
Acesse aqui a resolução detalhada dessa atividade.
Atividades complementares: Clique aqui para imprimir
Resolução das atividade complementares, clique aqui para imprimir.
Possíveis soluções:
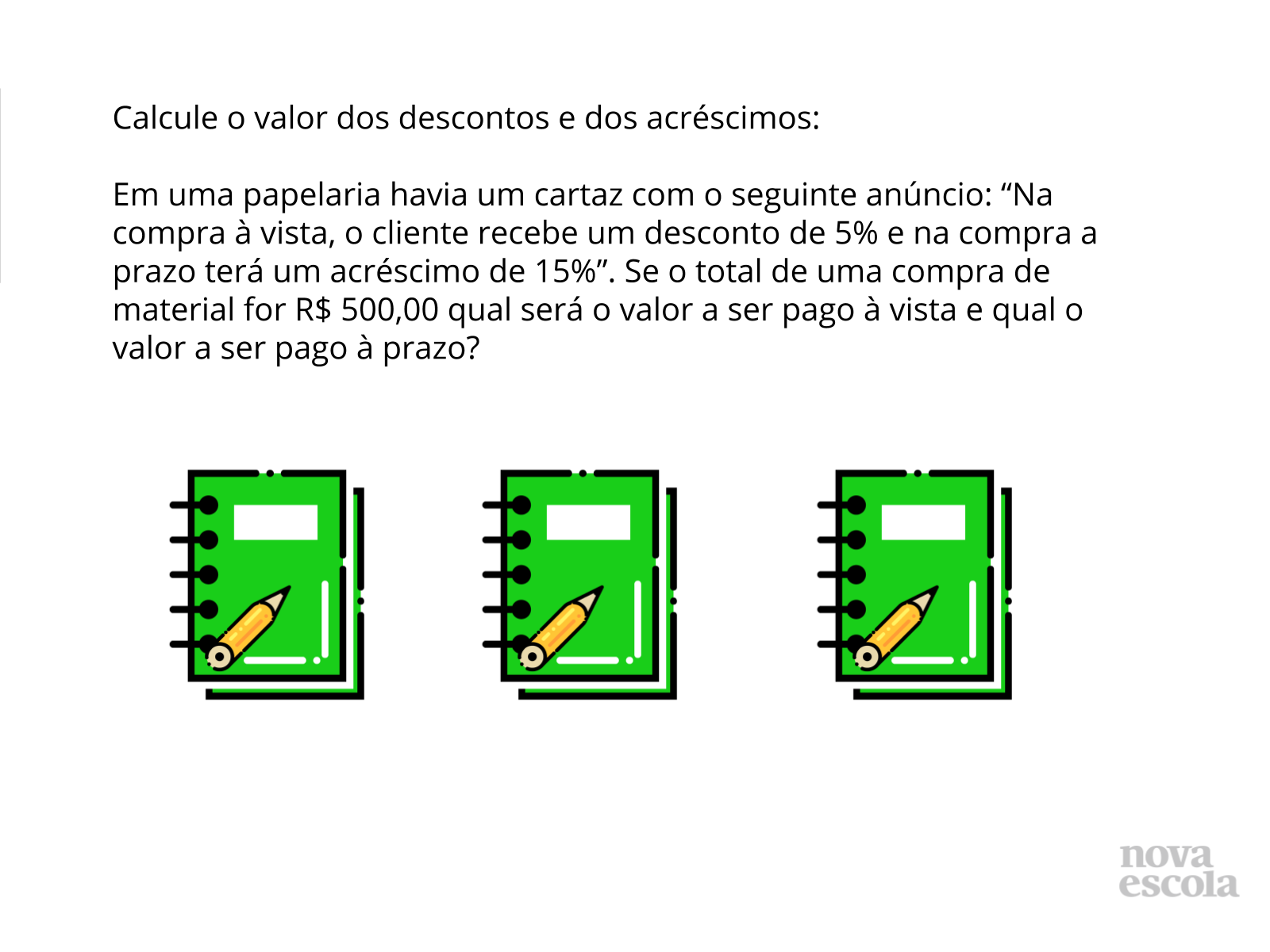
Calcule o valor dos descontos e dos acréscimos:
Em uma papelaria havia um cartaz com o seguinte anúncio: “Na compra à vista, o cliente recebe um desconto de 5% e na compra a prazo terá um acréscimo de 5%”. Se o total de uma compra de material for R$ 500,00 qual será o valor a ser pago a vista e qual o valor a ser pago à prazo?
Resolução:
Com o acréscimo o valor da compra ficará R$ 525,00 e com o desconto o valor da compra ficará R$ 475,00.
Materiais complementares:
Atividade raio x
Atividade complementar
Resolução atividade raio x
Resolução atividade complementar