Aquecimento
Plano de Aula
Plano de aula: Conceituando porcentagem
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Cálculo de porcentagens sem “regra de três”
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Marytta Rennó Masseli
Mentora: Débora Vieira de Moraes
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF06MA12 - Resolver e elaborar problemas que envolvam porcentagens, com base na ideia de proporcionalidade, sem fazer uso da “regra de três”, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros.
Objetivos específicos
Conceituar porcentagens de uma quantidade usando a fração centesimal e a representação decimal.
Conceito-chave
Conceituar porcentagem.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não.
- Folha quadriculadas, malhas de 10x10.
Habilidades BNCC:
Objetivos de aprendizagem
Conceituar porcentagens de uma quantidade usando a fração centesimal e a representação decimal.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Aula
Resumo da aula
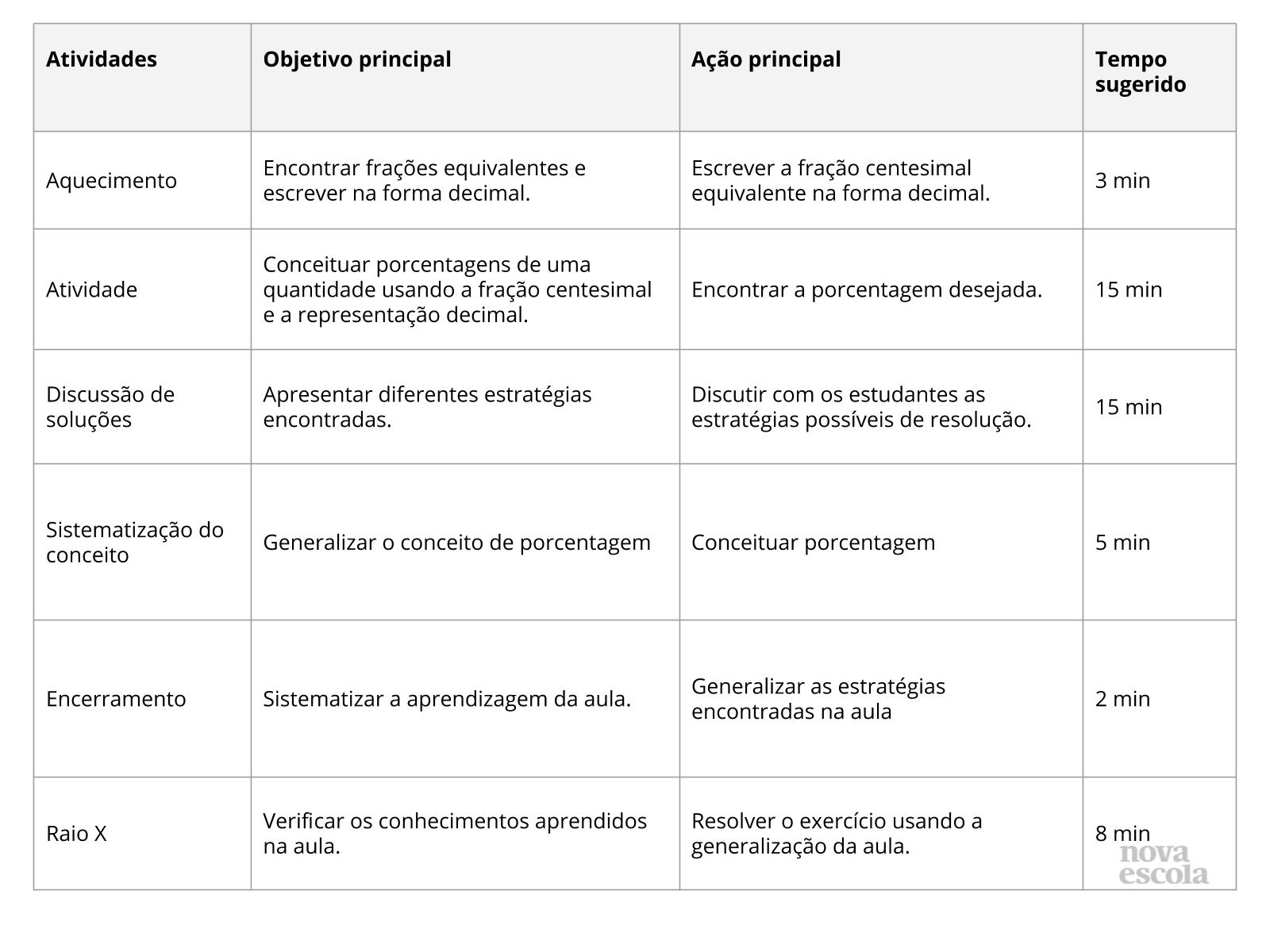
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.”
Objetivo

Tempo sugerido: 2 min
Orientação: Apresente o objetivo, através da leitura, escrita no quadro ou projeção do mesmo.
Deve-se ter como foco a construção do conhecimento de forma que os estudantes concluam, através da atividade principal, generalizações do conceito de porcentagem.
Também é importante manter o vocabulário matemático, como por exemplo:
- Frações equivalentes e não iguais.
- Frações centesimais
- Leitura dos números decimais, como: 0,1 é um décimo, 0,01 é um centésimo, 0,5 são cinco décimos, 1,0 são cem centésimos ou um inteiro, 0,2 são dois décimos, 0,25 são vinte e cinco centésimos.
Propósito: Conceituar porcentagem.
Discuta com a turma:
- O que cada um pensa que significa porcentagem?
- O que o nome lembra matematicamente?
Adequações:
- Caso seja possível, pode-se fazer o trabalho com o uso da calculadora para encontrar a fração centesimal equivalente.
- Caso não seja possível a impressão das atividades pode-se passar as atividades no quadro, bem como para a malha de 100x100 pode-se usar papel quadriculado.
- Para estudantes com problemas de visão (baixa visão) pode-se solicitar material ampliado, ou escrever na cartolina, em uma escala grande.
- Para estudantes com outras especificidades pode-se utilizar material concreto como material dourado.
Material Complementar:
Sugere-se a leitura do Capítulo 3 da dissertação “Uma proposta de ensino de frações voltada para a construção do conhecimento” - acesse o link: http://bit.ly/2ByWcg2
O link http://bit.ly/2EgTxdC tem como sugestão o uso do jogo no ensino de fração.
Novo curso gratuito

Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO








