Resumo da aula
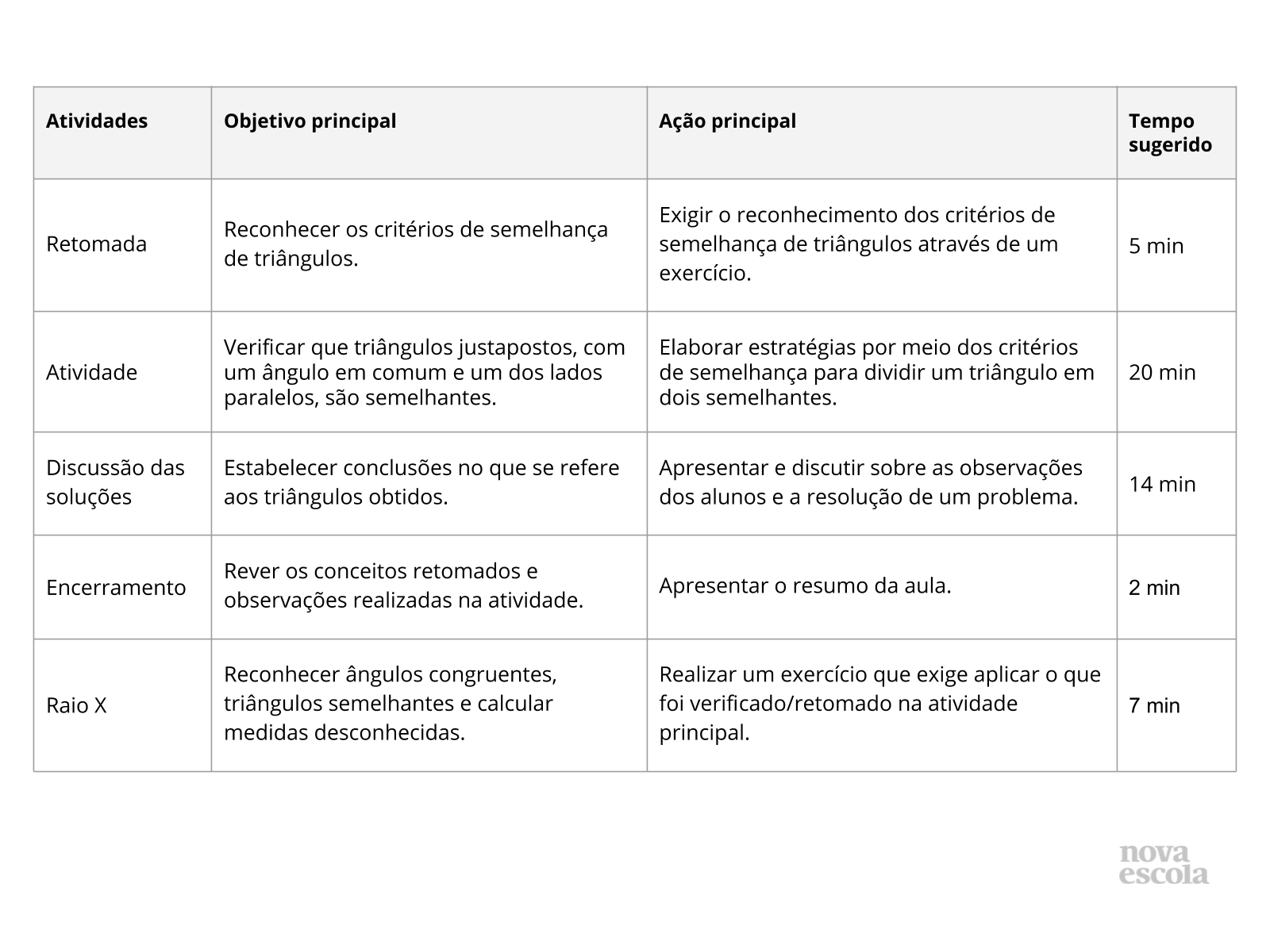
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 5 minutos.
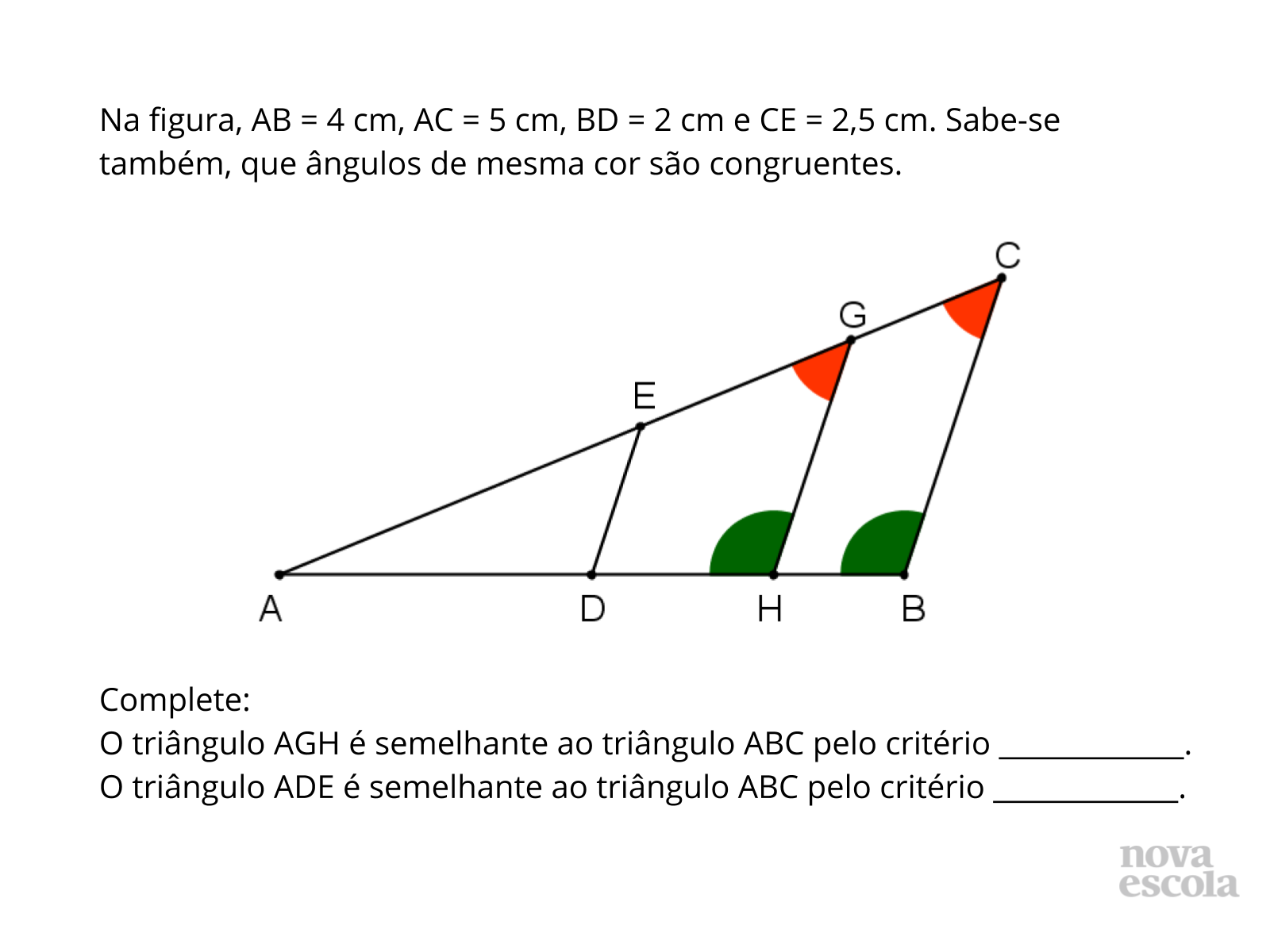
Orientações: Deixe que os alunos leiam a atividade e resolvam no caderno.
Propósito: Reconhecer os critérios de semelhança de triângulos.
Discuta com a turma:
- Qual critério de semelhança de triângulos não apareceu na atividade?
- Qual(is) medida(s) seriam necessárias para utilizar esse critério?
Materiais complementares:
Atividade aquecimento
Resolução da atividade de aquecimento
Atividade principal
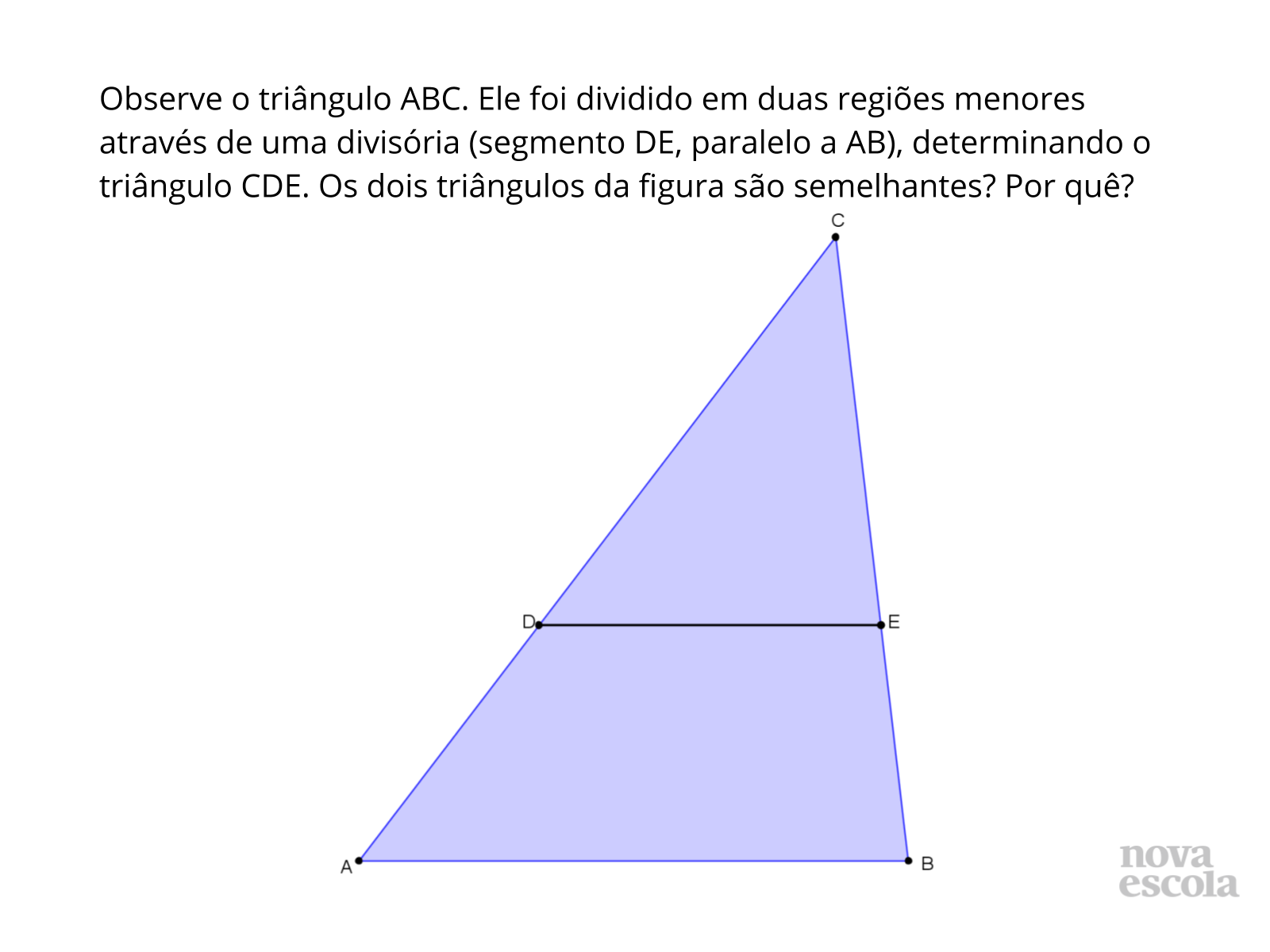
Tempo sugerido: 20 minutos (slides 4 a 10).
Orientações: Peça que, individualmente, os alunos leiam a atividade e façam o que é solicitado.
Propósito: Verificar que triângulos justapostos, com um ângulo em comum e um dos lados paralelos, são semelhantes, por meio dos critérios de semelhança.
Discuta com a turma:
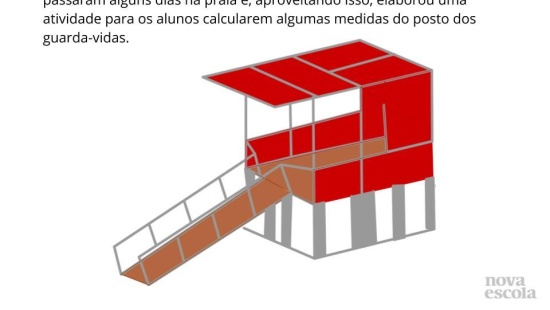
- Que informações a figura disponibiliza?
- De que maneira pode-se verificar a semelhança ou não desses triângulos, somente com essas informações?
Materiais complementares:
Atividade principal
Resolução da atividade principal
Guia de intervenções
Atividade principal
Tempo sugerido: 20 minutos (slides 4 a 10).
Orientações: Peça que os alunos organizem os materiais necessários para dar sequência à atividade. Distribua também uma folha sulfite para cada aluno.
Propósito: Verificar que triângulos justapostos, com um ângulo em comum e um dos lados paralelos, são semelhantes, por meio dos critérios de semelhança.
Atividade principal

Tempo sugerido: 20 minutos (slides 4 a 10).
Orientações: Peça que, individualmente, os alunos leiam a atividade. As construções podem ser realizadas passo a passo no quadro juntamente com os alunos caso eles apresentem dificuldades.
Propósito: Verificar que triângulos justapostos, com um ângulo em comum e um dos lados paralelos, são semelhantes, por meio dos critérios de semelhança.
Atividade principal
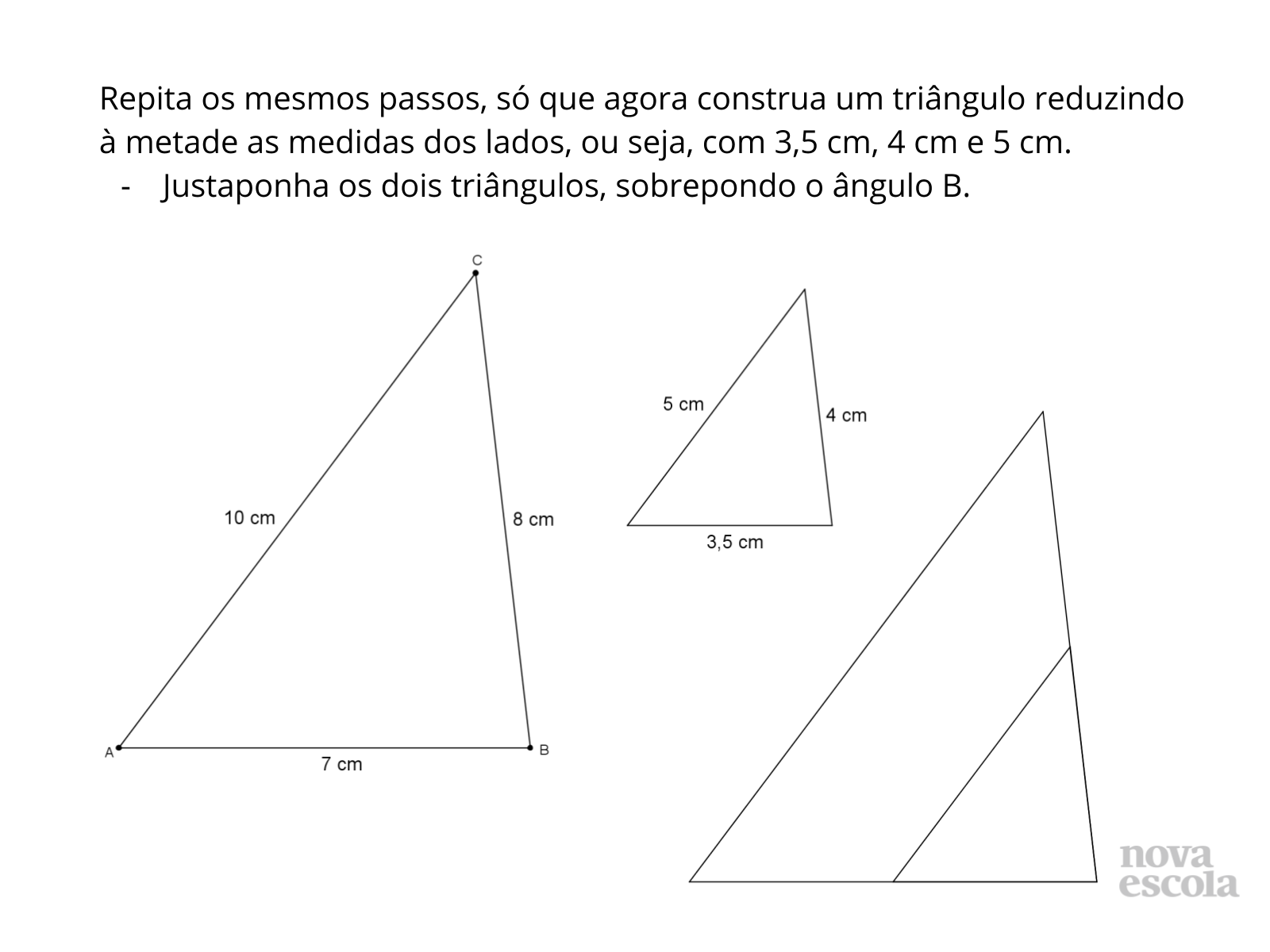
Tempo sugerido: 20 minutos (slides 4 a 10).
Orientações: As construções podem ser realizadas passo a passo no quadro juntamente com os alunos caso eles apresentem dificuldades.
Propósito: Verificar que triângulos justapostos, com um ângulo em comum e um dos lados paralelos, são semelhantes, por meio dos critérios de semelhança.
Discuta com a turma:
- Em qual critério de semelhança de triângulos essa estratégia se baseou?
- Com esta estratégia, é possível ainda propor uma divisória diferente? De que maneira?
Atividade principal
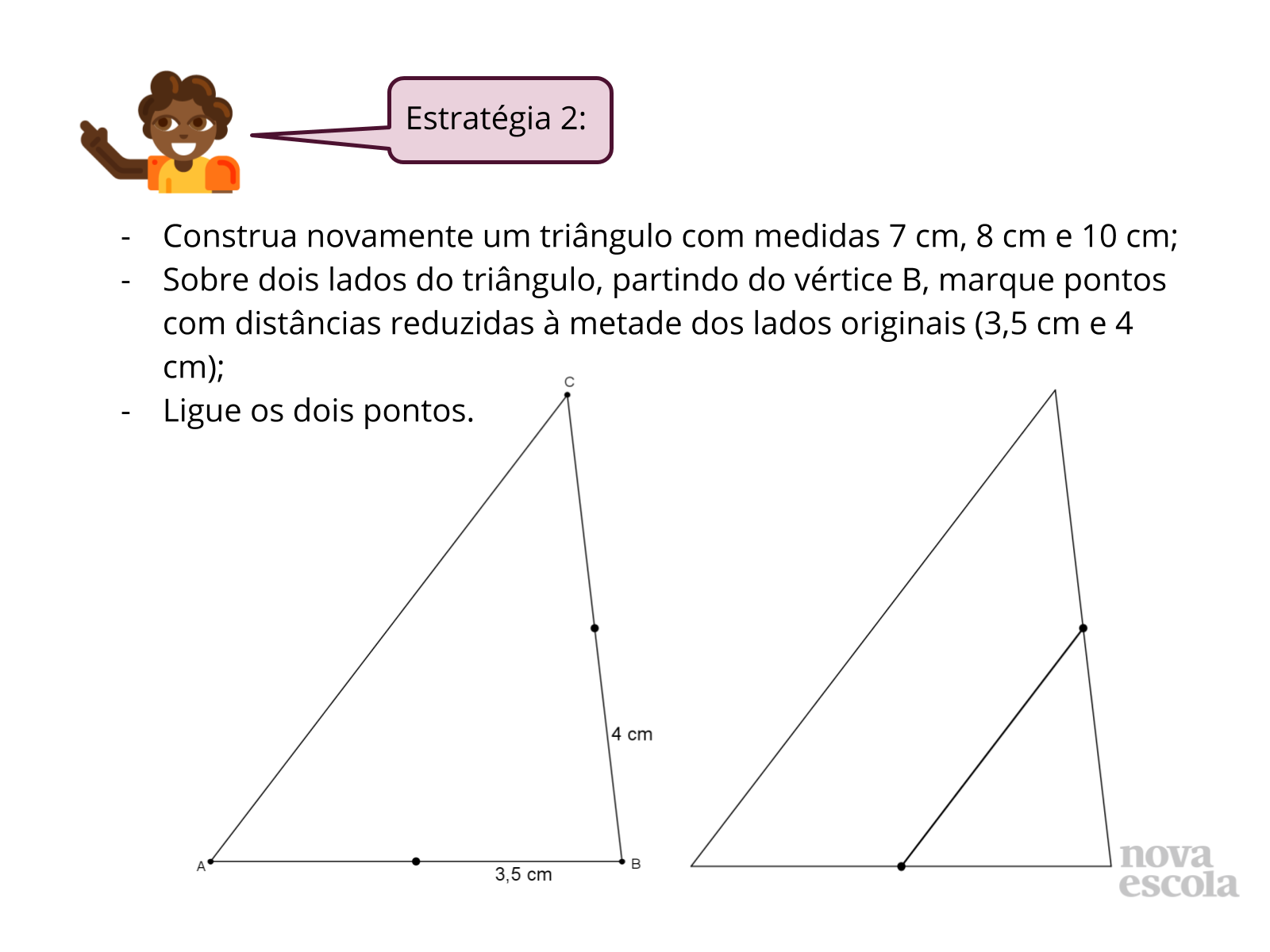
Tempo sugerido: 20 minutos (slides 4 a 10).
Orientações: Circule na sala para verificar se os alunos compreenderam os passos dessa estratégia.
Propósito: Verificar que triângulos justapostos, com um ângulo em comum e um dos lados paralelos, são semelhantes, por meio dos critérios de semelhança.
Discuta com a turma:
- Em qual critério de semelhança de triângulos essa estratégia se baseou?
- Com esta estratégia, é possível ainda propor uma divisória diferente? De que maneira?
Atividade principal

Tempo sugerido: 20 minutos (slides 4 a 10).
Orientações: Peça que os alunos organizem-se em duplas e discutam para elaborar uma estratégia de resolução. Comente com os alunos que eles podem, se precisarem, utilizar os materiais citados. Oriente os alunos a não se preocuparem com o tamanho de cada parte do triângulo ABC, e sim que a divisória determine dois triângulos semelhantes. Em um primeiro momento, não realize nenhuma intervenção, apenas circule pela sala para ter uma ideia do andamento do trabalho e da estratégia que os alunos estão utilizando. Se alguma dupla tiver dificuldades e pedir seu auxilio, aí sim intervenha, no sentido de entender o que já pensaram e a partir daí, elaborarem um plano de resolução.
Propósito: Verificar que triângulos justapostos, com um ângulo em comum e um dos lados paralelos, são semelhantes, por meio dos critérios de semelhança.
Atividade principal
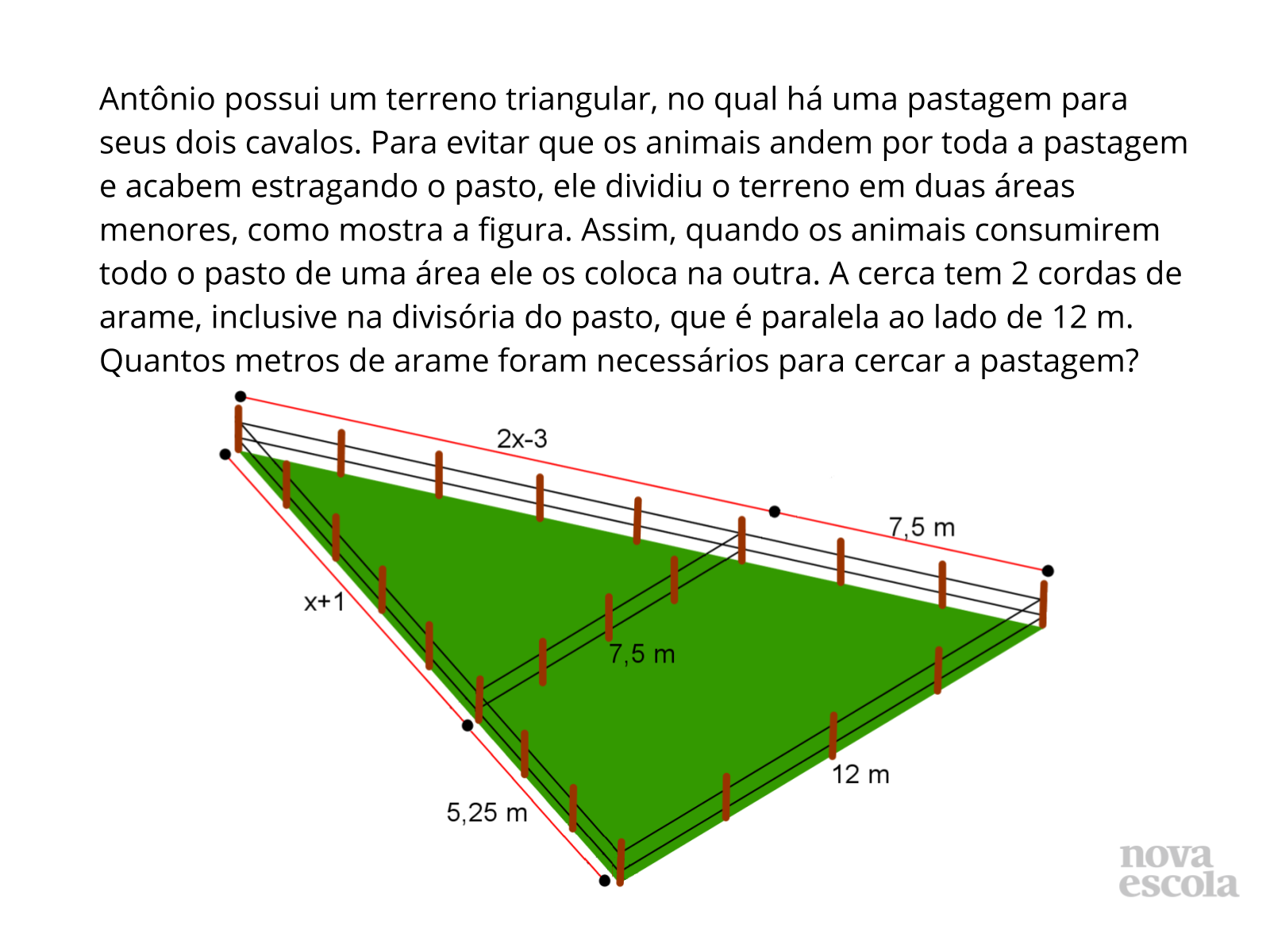
Tempo sugerido: 20 minutos (slides 4 a 10).
Orientações: Peça que os alunos organizem-se em duplas e discutam para elaborar uma estratégia de resolução.
Propósito: Verificar que triângulos justapostos, com um ângulo em comum e um dos lados paralelos, são semelhantes, por meio dos critérios de semelhança.
Discuta com a turma:
- Qual é a incógnita do problema? (o que o problema quer como resposta?)
- Que medidas são necessárias para calcular o que o problema solicita? Todas estão disponíveis?
Discussão de soluções

Tempo sugerido: 14 minutos (slides 11 a 15).
Orientações: Convide alguns alunos a exporem o que observaram. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos. Certifique-se que todos entenderam porque os triângulos são semelhantes.
Propósito: Discutir com os alunos as respostas obtidas e observações realizadas para verificar a semelhança entre os dois triângulos presentes na figura.
Discuta com a turma:
- Por que os triângulos são semelhantes? Como podemos verificar/demonstrar essa semelhança?
Discussão de soluções
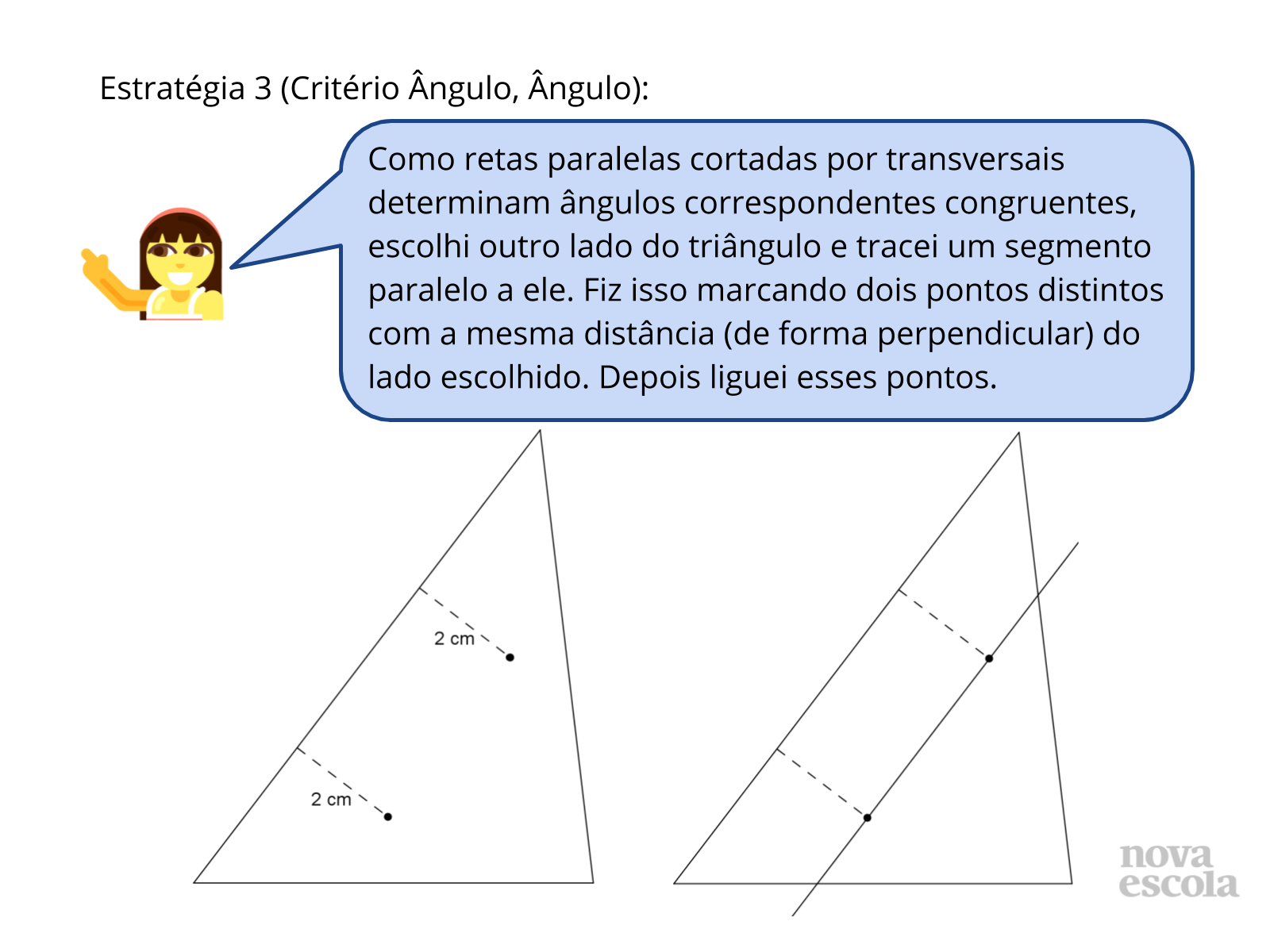
Tempo sugerido: 14 minutos (slides 11 a 15).
Orientações: Convide alguns alunos a expor de que maneira propuseram a nova divisória, levando em consideração o critério AA. Se surgirem estratégias diferentes, solicite que cada aluno anote pelo menos uma estratégia diferente da sua. Este slide apresenta uma possível maneira de representar a nova divisória.
Propósito: Validar as estratégias utilizadas pelos alunos e perceber a utilização dos critérios de semelhança de triângulos.
Discuta com a turma:
- Com esta estratégia, é possível ainda propor uma divisória diferente? De que maneira?
Discussão de soluções
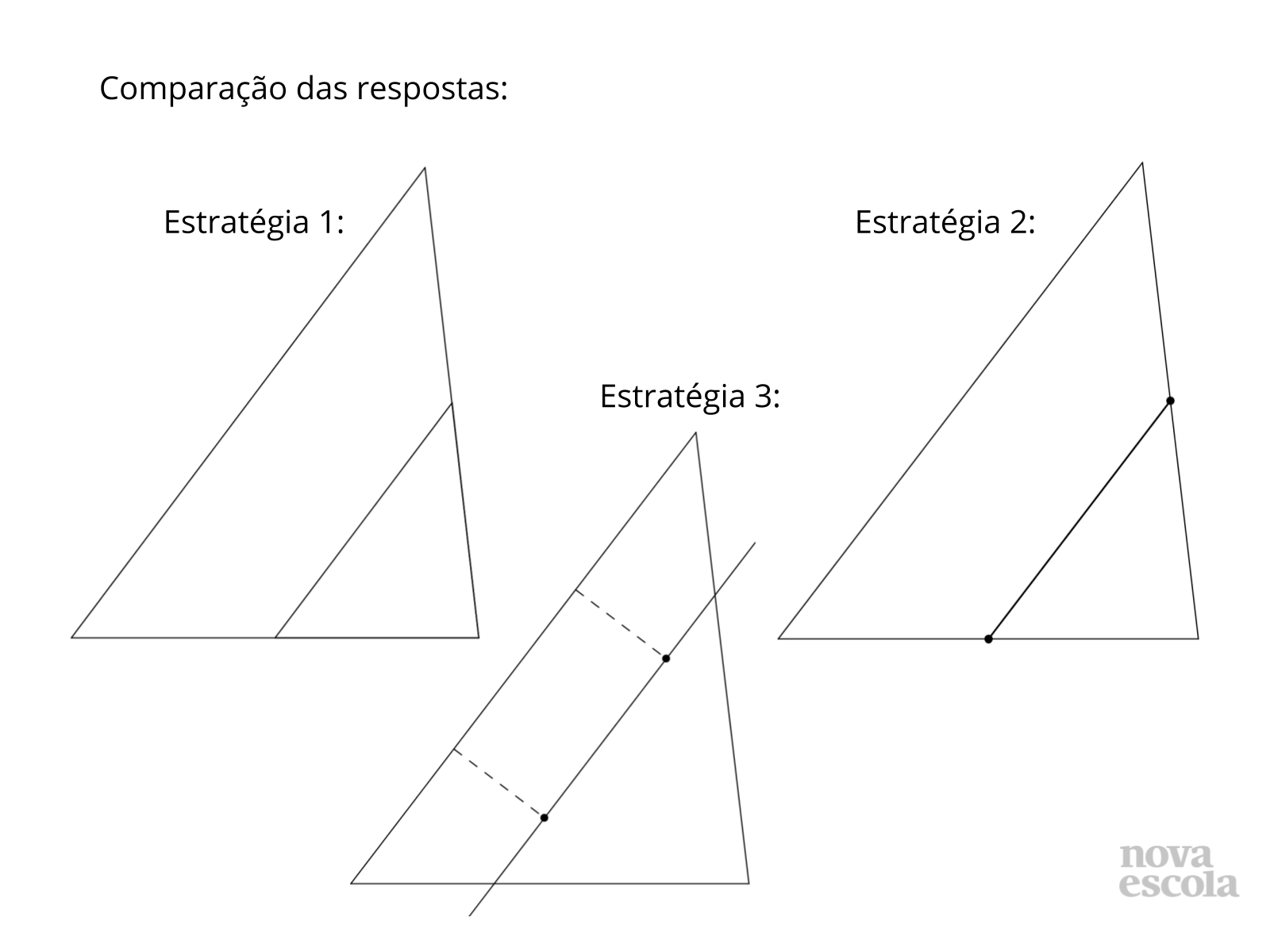
Tempo sugerido: 14 minutos (slides 11 a 15).
Orientações: Compare as respostas apresentadas e peça para que os alunos analisem e tentem encontrar diferenças e semelhanças.
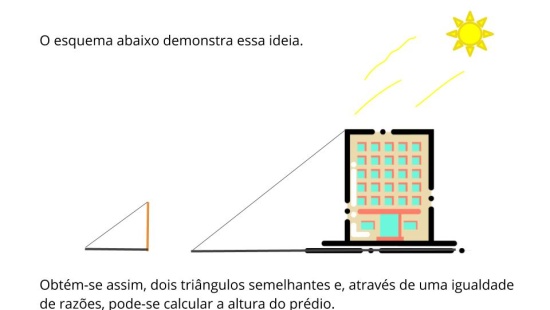
Propósito: Verificar que uma reta paralela a um lado de um triângulo, determina um triângulo semelhante ao primeiro.
Discuta com a turma:
- Quais as diferenças entre cada resposta apresentada?
- Quais foram as semelhanças? Há alguma característica comum entre todas as divisórias propostas?
Discussão de soluções
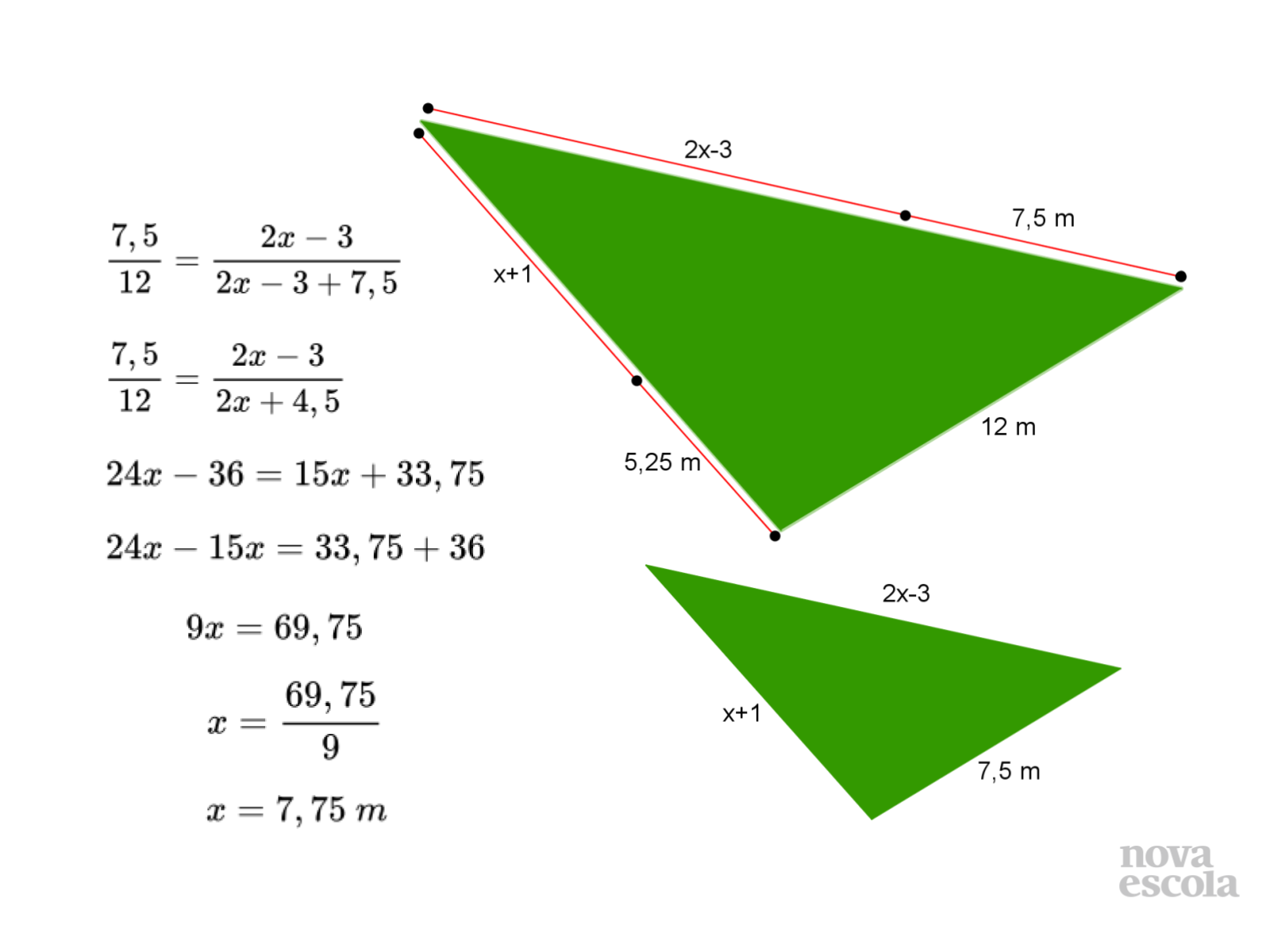
Tempo sugerido: 14 minutos (slides 11 a 15).
Orientações: Convide alguns alunos a expor o que observaram. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Discutir como os alunos montaram a proporção para obter as medidas desconhecidas.
Discuta com a turma:
- Através de que conceito vocês puderam resolver o problema?
- É possível encontrar o valor de x montando uma proporção diferente? Qual?
Discussão de soluções
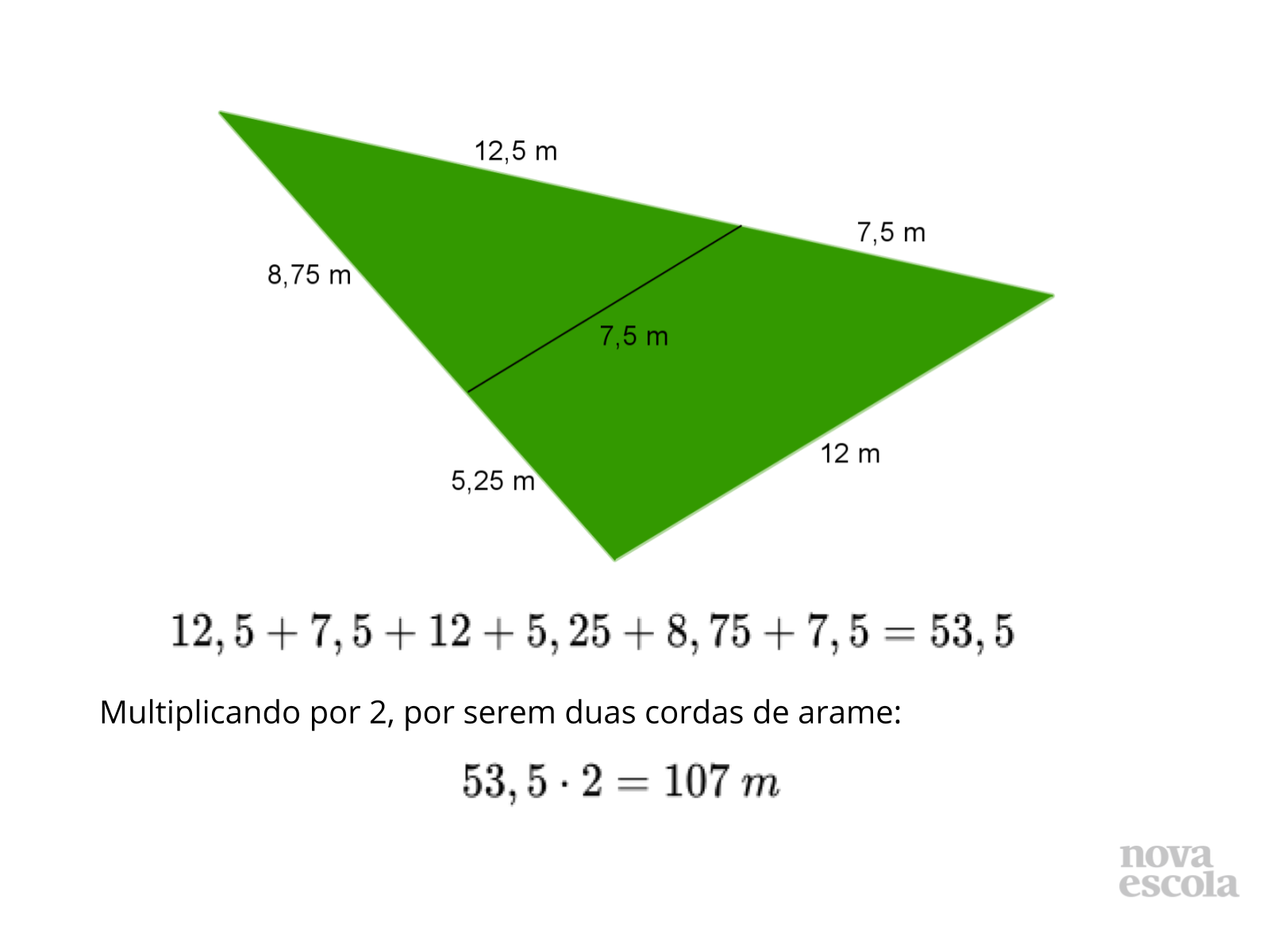
Tempo sugerido: 14 minutos (slides 11 a 15).
Orientações: Convide alguns alunos a expor o que observaram. Neste momento, os alunos deverão refletir sobre suas respostas através de seus questionamentos.
Propósito: Chegar a resposta final do problema.
Discuta com a turma:
- A soma de todas essas medidas, com exceção da medida da divisória, é o cálculo do quê?
Encerramento
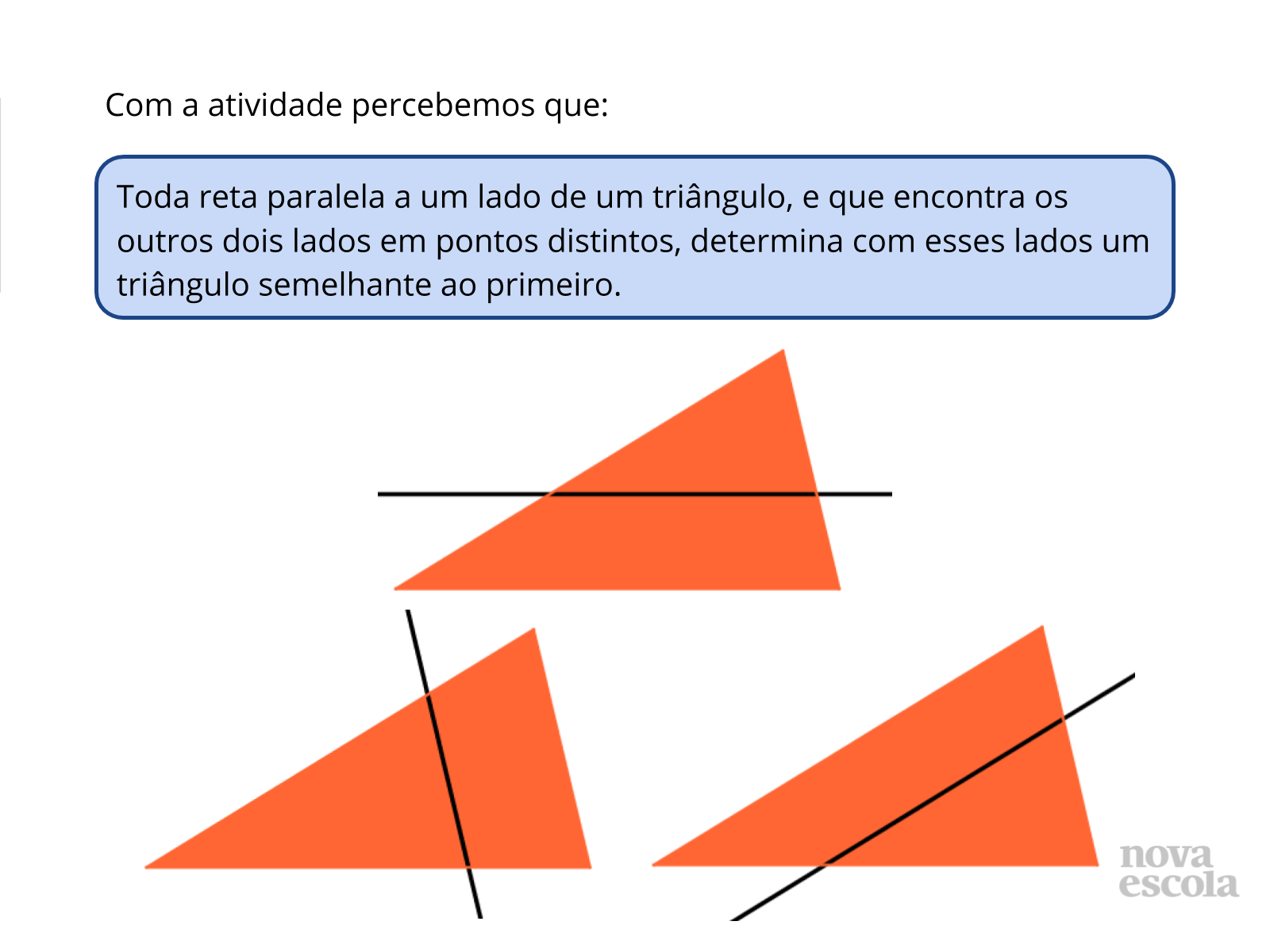
Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes a atividade que foi realizada e peça que leiam a conclusão e registrem no caderno.
Propósito: Retomar os conceitos envolvidos na atividade principal.
Raio X
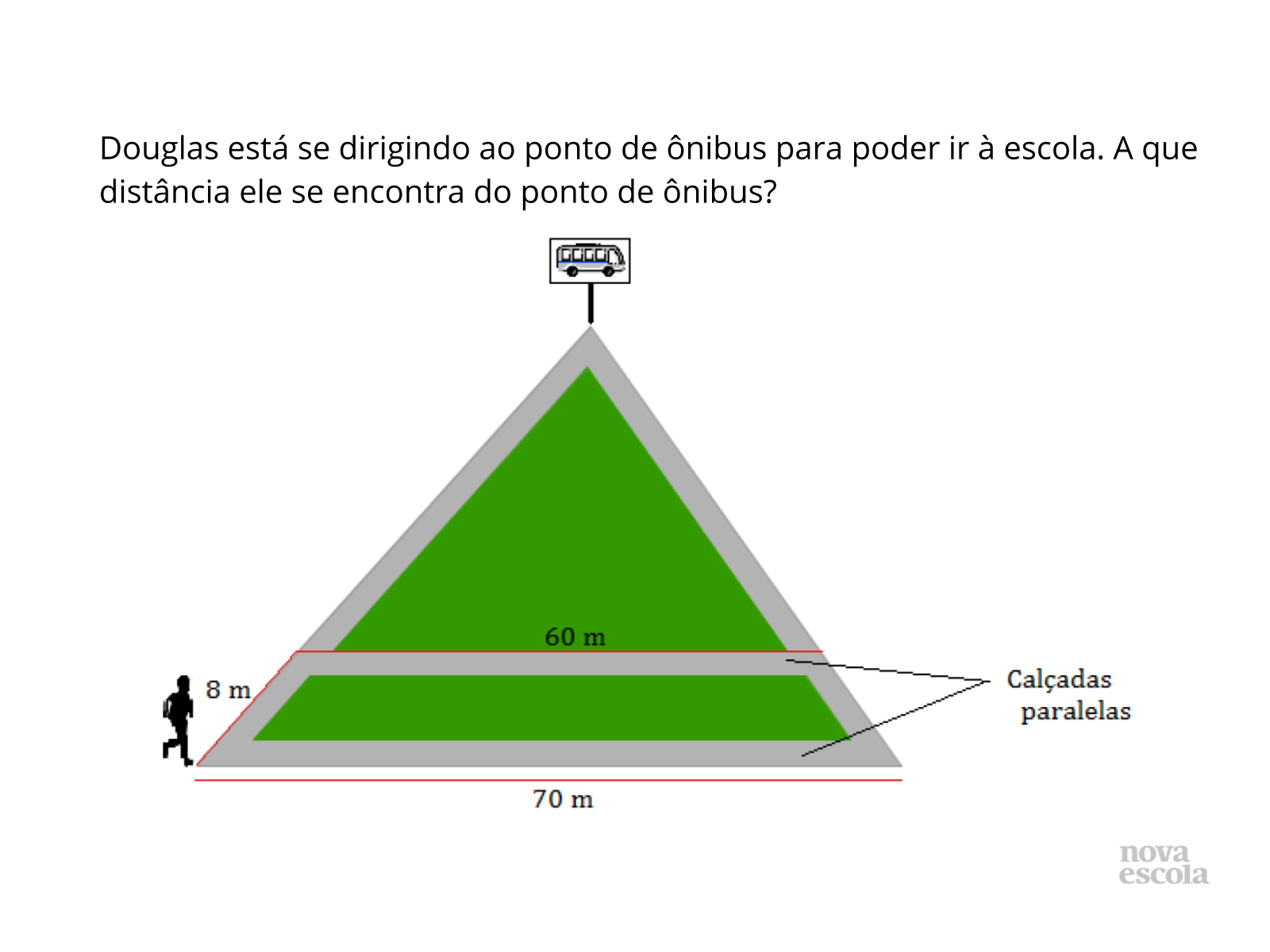
Tempo sugerido: 7 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Propósito: Verificar se os alunos reconhecem os triângulos semelhantes e conseguem montar a proporção corretamente para obter a medida desconhecida.
Discuta com a turma:
- Quais foram os triângulos visualizados para resolver o problema?
- Qual informação possibilita afirmar que os dois triângulos são semelhantes?
- Qual é o critério de semelhança que nos permite assegurar que esses triângulos são semelhantes?
- Quais são os ângulos congruentes?
Materiais complementares:
Atividade complementar
Atividade Raio X
Resolução da atividade complementar
Resolução do Raio X