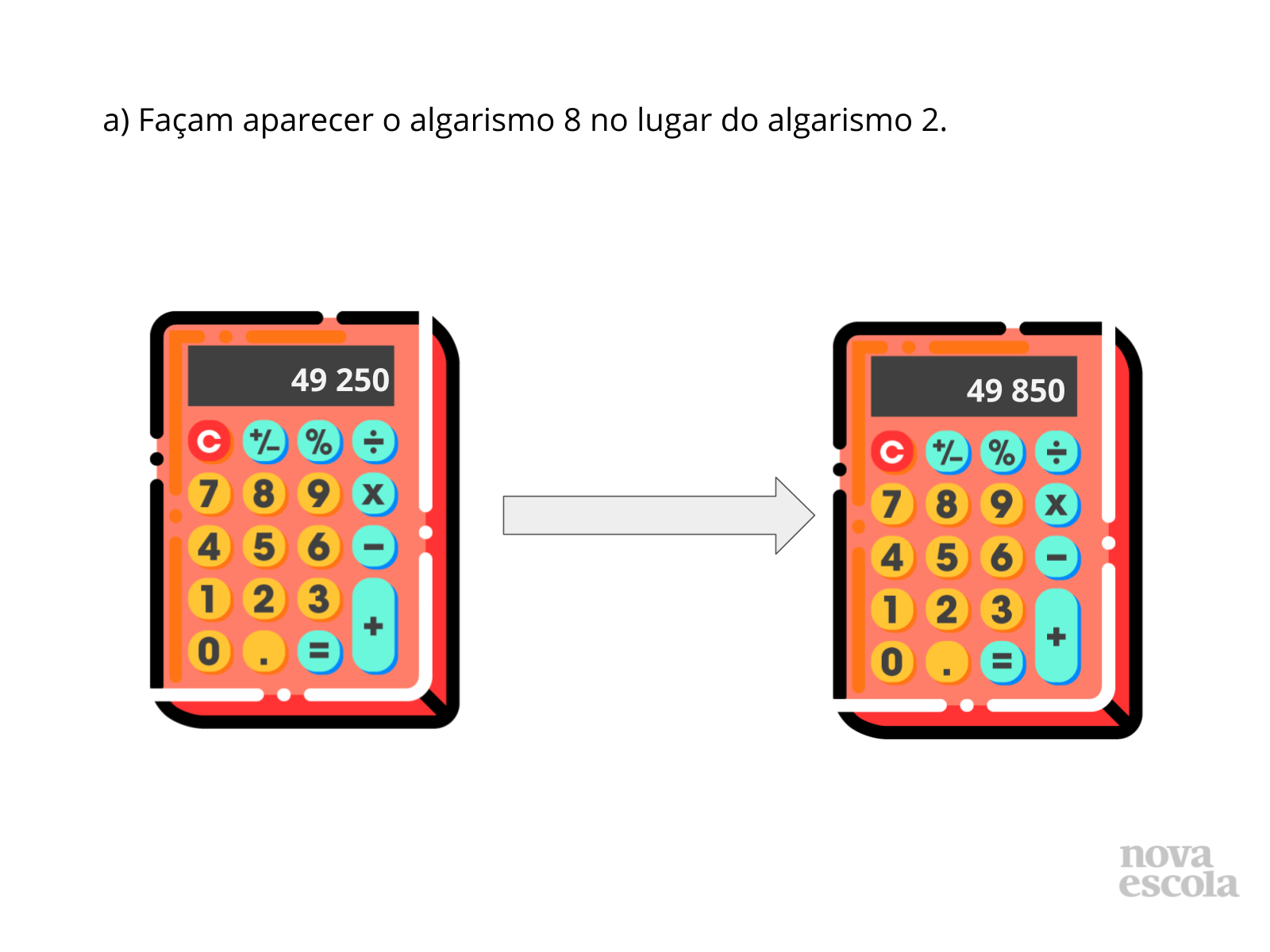
Atividade principal
Plano de Aula
Plano de aula: Representando números naturais
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Composição e decomposição de números naturais
Por: Cíntia Diógenes
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Cíntia Diógenes
Mentora: Elisa Greenhalgh Vilalta
Revisora pedagógica: Eliane Zanin
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA02 - Mostrar, por decomposição e composição, que todo número natural pode ser escrito por meio de adições e multiplicações por potências de dez, para compreender o sistema de numeração decimal e desenvolver estratégias de cálculo.
Objetivos específicos
- Identificar o valor posicional dos algarismos representados nos números e representá-los no quadro de pregas;
- Compreender a função do zero na representação de números no Sistema de Numeração Decimal e utilizá-lo adequadamente.
Conceito-chave
Representação de números naturais utilizando seus valores posicionais.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Cartões coloridos;
- CAVALU (Cartaz de Valor de Lugar);
- Ábaco aberto;
- Projetor ( opcional).
Habilidades BNCC:
Objetivos de aprendizagem
- Identificar o valor posicional dos algarismos representados nos números e representá-los no quadro de pregas;
- Compreender a função do zero na representação de números no Sistema de Numeração Decimal e utilizá-lo adequadamente.
Resumo da aula
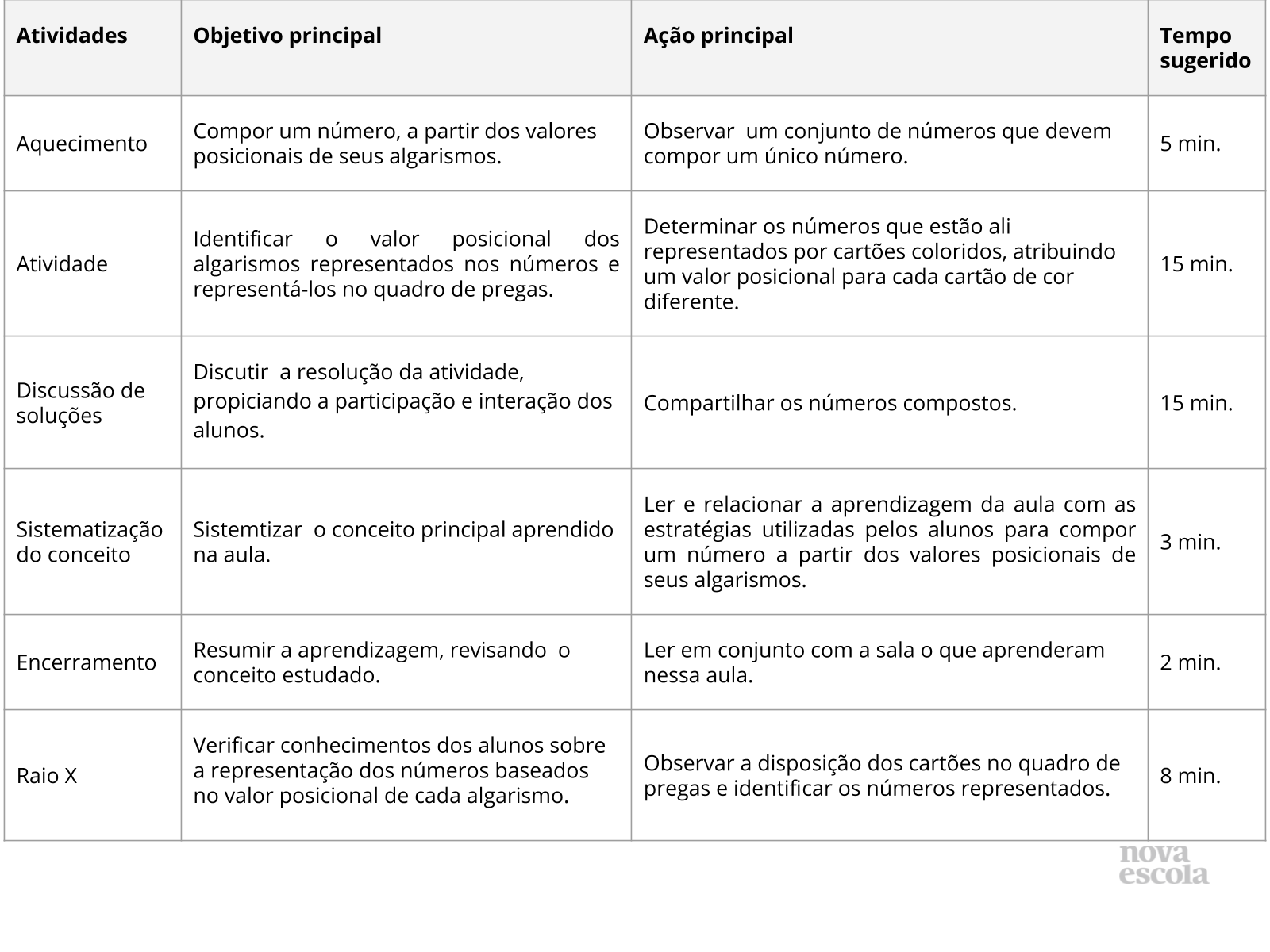 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo previsto: 5 minutos.
Orientações: Projete este slide ou escreva no quadro. Depois peça para que as crianças observem os números dentro do quadro. Questione a turma sobre a possibilidade de formar um único número, composto a partir das quantidades que estão sendo apresentadas. Peça para as crianças pensarem e, em seguida, compartilharem com a turma de que forma realizaram essa composição. Esse é um momento no qual deve ser aberto para discussão. As crianças devem comparar as estratégias que cada um apresentou, verificando as semelhanças e diferenças e o que foi possível perceber sobre a composição dos números no Sistema de Numeração Decimal, a partir dessa atividade. As crianças devem perceber que cada algarismo de um número possui um valor posicional de base 10.
Discuta com a turma:
- Quais os números que estão no quadro?
- Com esses números poderíamos formar um único número?
- Como você faria para compor esse número, a partir dos que estão no quadro?
- Observando os números do quadro, há alguma regularidade entre eles?
- É possível escrevê-los em ordem decrescente? O que você observa?
- Quantos zeros há em cada número do quadro? Isso indica algo para você?
- Então, qual o número que é composto a partir dos números do quadro? Explique para os seus colegas como chegou à essa conclusão.
Propósito: Compor um número, a partir dos valores posicionais de cada um dos seus algarismos.
Resposta esperada:
O número composto a partir dos números do quadro é 42 593.
Atividade principal
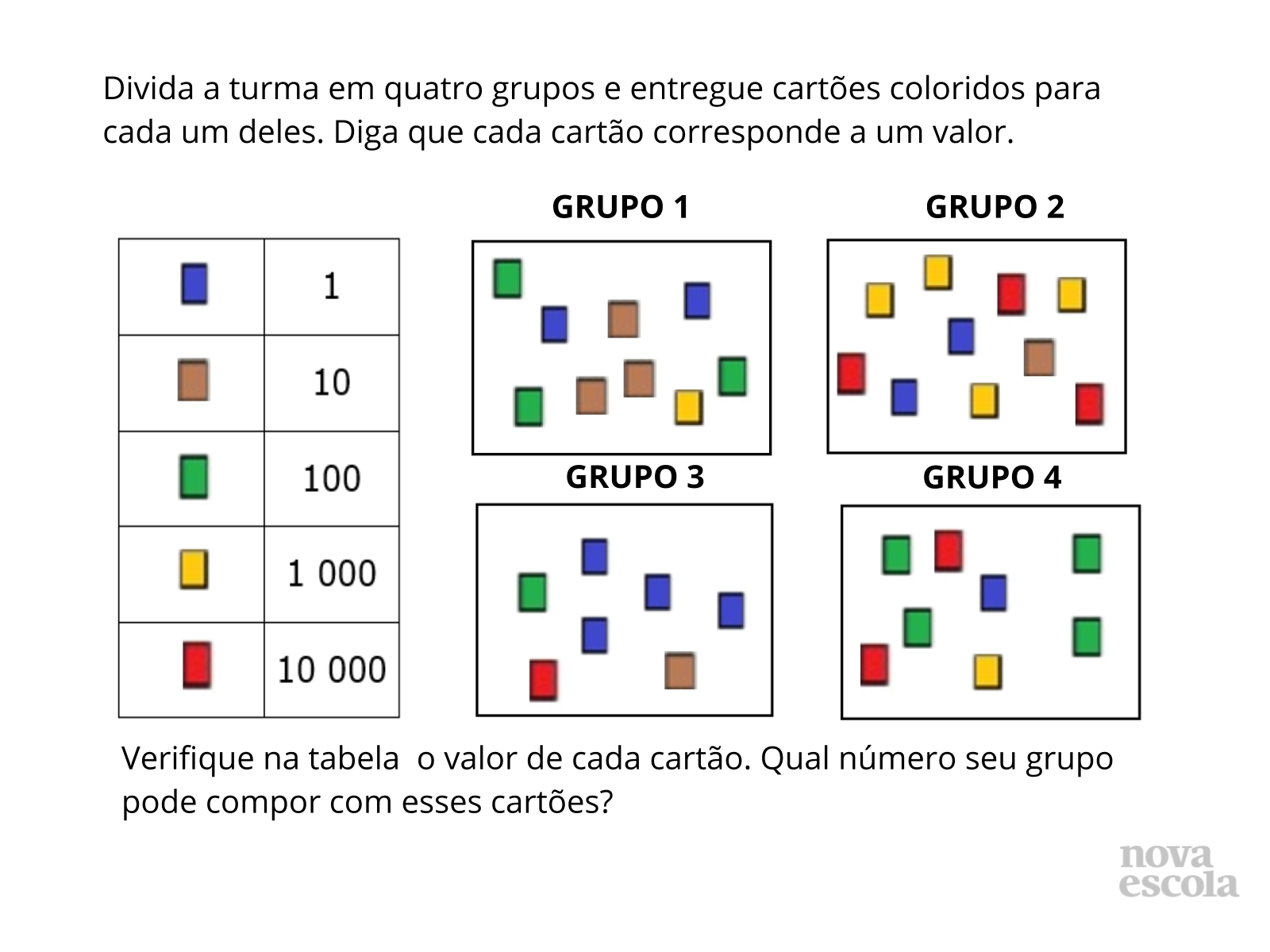
Tempo sugerido: 15 minutos.
Orientações: Inicie a atividade dividindo a turma em quatro grupos. Não importa o número de participantes em cada grupo, o importante é que sejam quatro grupos. Entregue a atividade impressa para cada grupo. Antes de apresentar a situação-problema, explique à turma que iremos realizar uma atividade cooperativa e que é muito importante a participação e envolvimento de todos os membros do grupo. Se achar interessante, é possível utilizar alguns minutos da atividade para estabelecer combinados gerais ou entre os membros de cada grupo para que a atividade seja produtiva e prazerosa. Após esse momento, entregue cartões coloridos, semelhantes aos apresentados na imagem da atividade e com a mesma quantidade, para cada grupo (Esse material precisa ser confeccionado e preparado com antecedência). Questione as crianças sobre o que elas acham que vamos fazer com esses cartões. É importante respeitar a fala de cada criança, valorizando sua ideia e levando a uma discussão com toda a turma acerca das propostas levantadas. Só então apresente para a turma a situação-problema da atividade. O professor esclarecerá que cada grupo está com os mesmos cartões de algum dos grupos da imagem dos próximos slides. Os alunos devem observar a quantidade de cartões recebidos e analisar seus valores no quadro entregue. O grupo deve criar estratégias, discutindo e problematizando, para responder à pergunta que aparece no fim da atividade. Enquanto os alunos estão interagindo em seus grupos, caminhe pela sala,e estimule a participação de todos os alunos e realize mediações.Consulte o guia com sugestões de intervenções.
Discuta com a turma:
- O que representa os cartões coloridos na atividade?
- Cada cartão representa que valor?
- Por que você acha que alguns grupos receberam vários cartões da mesma cor?
- Ao grupo 1 ( Seu grupo recebeu três cartões marrons. O que isso representa?) Siga com esses questionamentos específicos a cada grupo.
- Existem grupos que não possuem uma cor de cartão. O que isso representa?
- Você consegue relacionar os cartões com as ordens dos números? Explique essa relação.
- Qual estratégia seu grupo pretende utilizar para responder à questão?
- Qual a maior dificuldade que seu grupo está enfrentando? Como vocês pretendem superá-la?
Propósito: Identificar o valor posicional dos algarismos representados nos números e representá-los no quadro de pregas.
Material para impressão:
Material complementar para o professor:
CAVALU - Cartaz Valor do Lugar
Fonte:
http://matematicaef2.blogspot.com.br/2011/03/aritmetica.html
O aprendizado do trabalho em grupo
Fonte:
https://novaescola.org.br/conteudo/605/o-aprendizado-do-trabalho-em-grupo
Aprendizagem cooperativa na sala de aula
Fonte:
Discussão de soluções
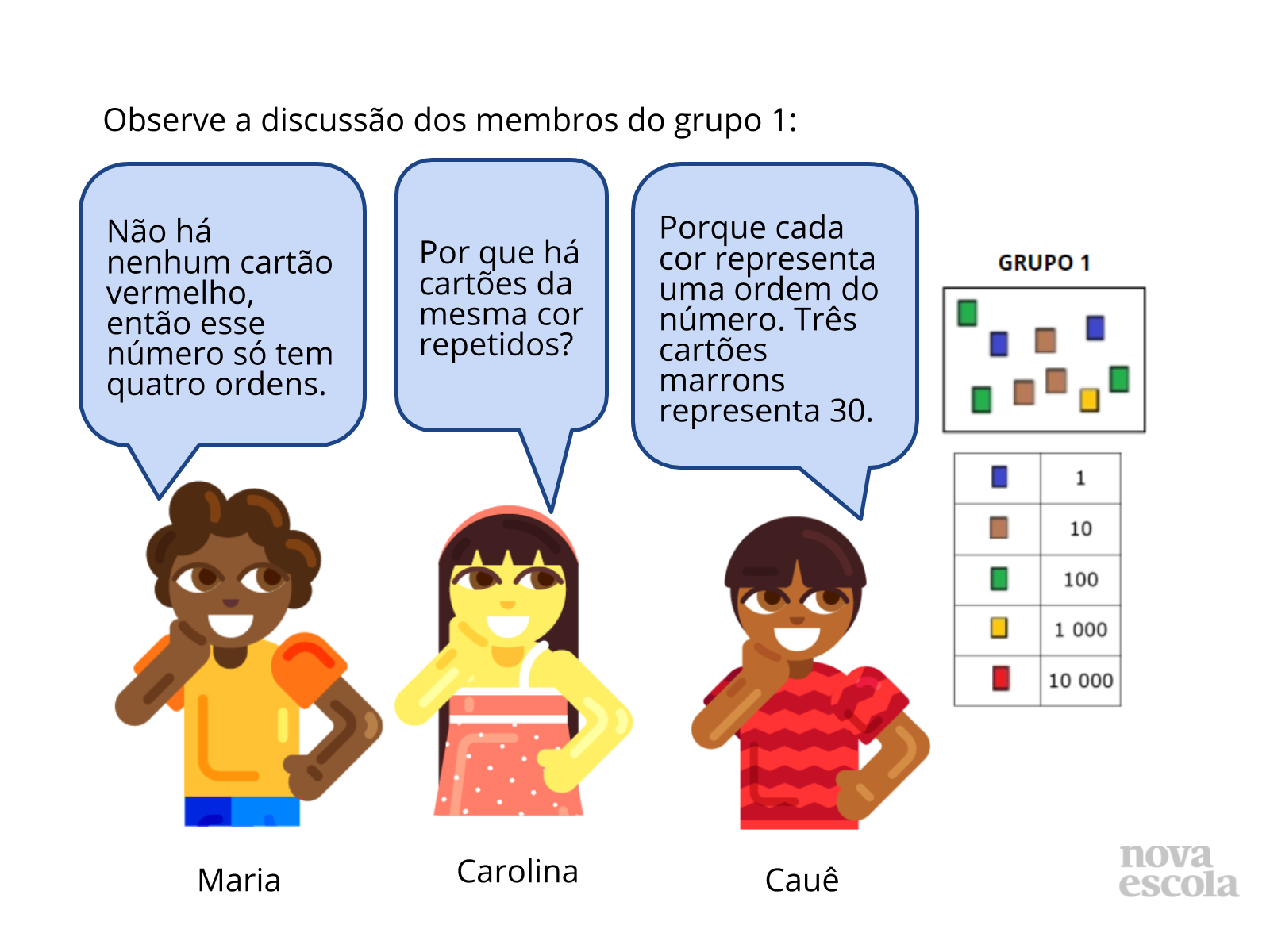
Tempo sugerido: 15 minutos.( slides 5 a 8)
Propósito: Compartilhar a resolução da atividade, propiciando a participação e interação dos alunos.
Orientações: Solicite que os alunos que compõem o grupo 1 na turma venham à frente e expliquem aos colegas quais as estratégias que utilizaram para sistematizar a solução do problema. Peça que eles expliquem o passo a passo do caminho traçado pelo grupo para alcançar a resposta, bem como as dificuldades que surgiram durante a resolução e como eles conseguiram superá-las. Depois a turma irá ler o slide de uma discussão hipotética acerca do problema do grupo 1. Após a leitura, a turma discutirá sobre as opiniões das crianças do slide, respondendo aos questionamentos e chegará à conclusão de qual seria o número representado pelos cartões entregue pelo professor para esse grupo. Para isso, é interessante que seja confeccionado um cartaz de valor de lugar (CAVALU) para que as crianças possam ir pregando os cartões em seus respectivos espaços para identificar o número composto por eles. Peça que as crianças leiam o número em voz alta.
Discuta com a turma:
- Quais as cores de cartões que o grupo tem?
- Quantos cartões há de cada cor?
- Qual o caminho traçado pelo grupo da sala para alcançar a resposta do problema?
- Quais as maiores dificuldades que o grupo enfrentou?
- Maria observou que não há nenhum cartão vermelho e que, por isso, o número só possui quatro ordens. Vocês concordam com ela? Por quê?
- Carolina está sentindo dificuldade quanto ao fato de haver cartões da mesma cor repetidos. Como você explicaria o motivo da repetição de cartões da mesma cor para ela? O que isso representa na composição do número?
- Você concorda com a explicação do Cauê? Você seria capaz de explicar de outra forma?
- É possível generalizar a resposta dada pelo Cauê para as outras ordens do número? Como você faria isso?
- Como estaria disposto os cartões no CAVALU da sala? Preguem os cartões no cartaz e discutam: O que é possível observar? Dispor os cartões no quadro ajuda a visualizar o número formado? Por quê?
- Qual é o número que o grupo deve compor?
Material Complementar:
Discussão de soluções

Tempo sugerido: 15 minutos.( slides 5 a 8)
Orientações: Dessa vez os alunos que compõem o grupo 2 na turma devem à frente e explicar aos colegas quais as estratégias que utilizaram para sistematizar a solução do problema. Solicite que o grupo explique todo o passo a passo para a resolução da atividade, com detalhes e expondo as dificuldades que enfrentaram, bem como a forma pela qual foram capazes de resolvê-las. Depois a turma irá ler o slide de uma discussão hipotética acerca do problema do grupo 2. Após a leitura, a turma discutirá sobre as opiniões das crianças do slide, respondendo aos questionamentos e chegará à conclusão de qual seria o número representado pelos cartões entregue pelo professor para esse grupo. Por fim, o grupo irá pregar os cartões no CAVALU da sala e apresentará o número encontrado. Peça que as crianças leiam o número em voz alta.
Discuta com a turma:
- Quais as cores de cartões que o grupo tem?
- Quantos cartões há de cada cor?
- Qual o caminho traçado pelo grupo da sala para alcançar a resposta do problema?
- Quais as maiores dificuldades que o grupo enfrentou?
- O que você acha da hipótese de Bruno? Por que você acha que ele chegou a essa conclusão? Ele está certo?
- Roberta concluiu que, como não há cartão verde, não pode haver nenhum algarismo na centena. Você concorda com a maneira que ela explicou? De que outra forma você explicaria isso, de forma mais clara?
- Pela ideia que Roberta traz, o número que Bruno propôs está correto? Explique.
- Como você responderia à pergunta de Guilherme?
- Como estaria disposto os cartões no CAVALU da sala? Pregue os cartões no cartaz e discutam: O que é possível observar? Dispor os cartões no quadro ajuda a visualizar o número formado? Por quê?
- Qual é o número que o grupo deve compor?
Propósito: Compartilhar a resolução da atividade, propiciando a participação e interação dos alunos.
Discussão de soluções

Tempo sugerido: 15 minutos.( slides 5 a 8)
Orientações: Agora os alunos que compõem o grupo 3 na turma devem à frente e explicar aos colegas quais as estratégias que utilizaram para sistematizar a solução do problema, apresentando o passo a passo com detalhes, o que discutiram, quais as maiores dificuldades que enfrentaram e como resolveram-nas. Depois a turma irá ler o slide de uma discussão hipotética acerca do problema do grupo 3. Após a leitura, abra a discussão para que as crianças opinem sobre o que está sendo exposto no slide, respondendo aos questionamentos e chegando à conclusão de qual seria o número representado pelos cartões entregue pelo professor para esse grupo. Por fim, o grupo irá pregar os cartões no CAVALU da sala e apresentará o número encontrado. Peça que as crianças leiam o número em voz alta.
Discuta com a turma:
- Quais as cores de cartões que o grupo tem?
- Quantos cartões há de cada cor?
- Qual o caminho traçado pelo grupo da sala para alcançar a resposta do problema?
- Quais as maiores dificuldades que o grupo enfrentou?
- Mariana disse já compreender algo. Você concorda com ela? Explique a afirmação dela com outras palavras.
- Daniel concordou com Mariana e compôs um número. Você acha que esse é o número correto? Explique.
- A informação que Ana traz confirma ou não o que Mariana e Daniel disseram?
- Que ordem representa o cartão azul? Qual o valor posicional de quatro cartões dessa cor? Por quê?
- Como estaria disposto os cartões no CAVALU da sala? Pregue os cartões no cartaz e discutam: O que é possível observar? Dispor os cartões no quadro ajuda a visualizar o número formado? Por quê?
- Qual é o número que o grupo deve compor?
Propósito: Compartilhar a resolução da atividade, propiciando a participação e interação dos alunos.
Discussão de soluções
Tempo sugerido: 15 minutos.( slides 5 a 8)
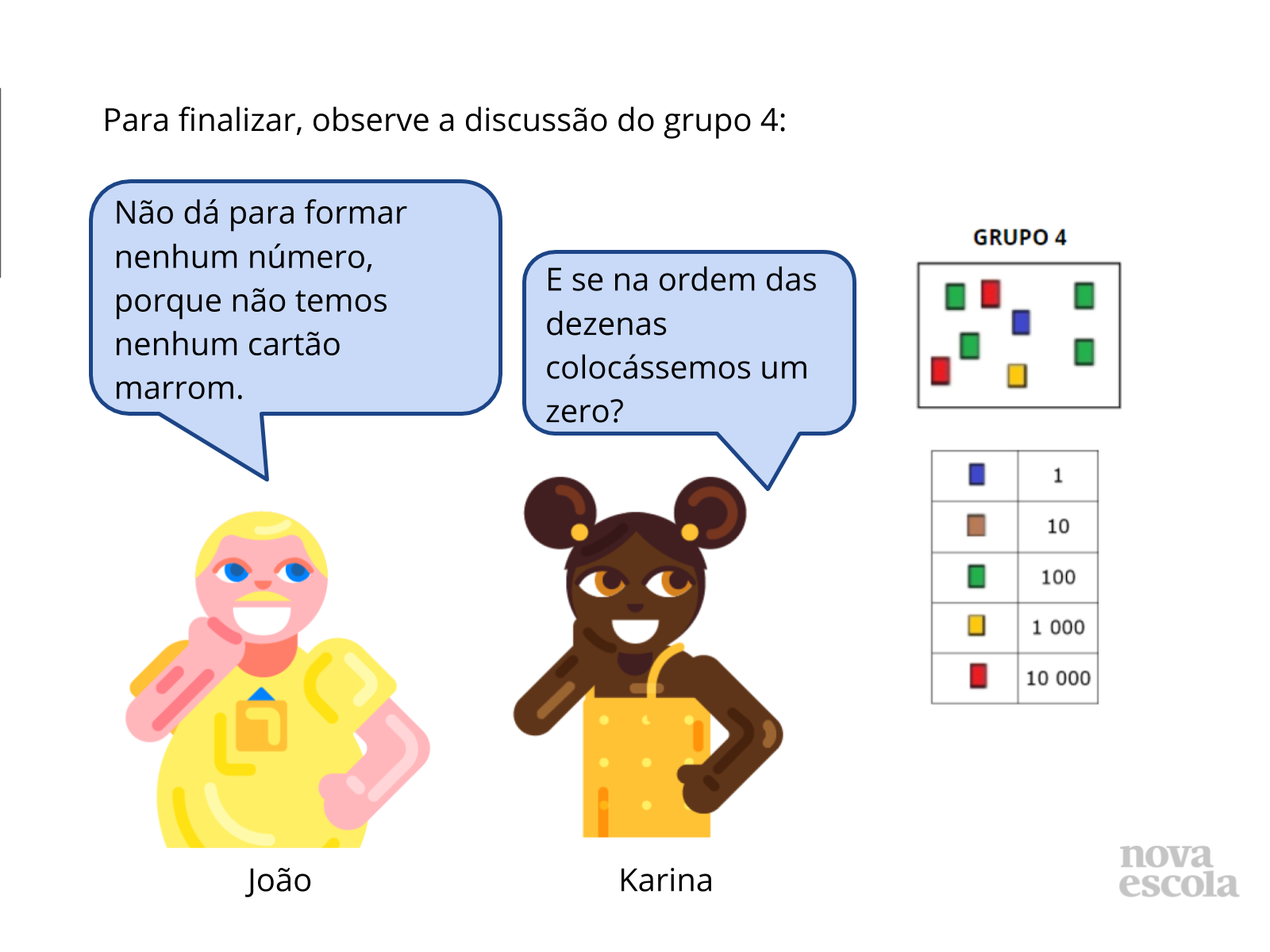
Orientações: Para finalizar a discussão das soluções, os alunos que compõem o grupo 4 na turma devem à frente e apresentar a solução da atividade, assim como os outros grupos fizeram. Depois a turma lerá o slide de uma discussão hipotética acerca do problema do grupo 4. Após a leitura, abra a discussão para que as crianças opinem sobre o que está sendo exposto no slide, respondendo aos questionamentos e chegando à conclusão de qual seria o número representado pelos cartões entregue pelo professor para esse grupo. Por fim, o grupo pregará os cartões no CAVALU da sala e apresentará o número encontrado. Peça que as crianças leiam o número em voz alta.
Discuta com a turma:
- Quais as cores de cartões que o grupo tem?
- Quantos cartões há de cada cor?
- Qual o caminho traçado pelo grupo da sala para alcançar a resposta do problema?
- Quais as maiores dificuldades que o grupo enfrentou?
- João disse que não é possível formar um número, porque não há cartão marrom. Você concorda com ele? Por quê?
- Karina propôs uma forma de resolver a dificuldade que o grupo está enfrentando. Como você explicaria o que ela está afirmando com outras palavras?
- Como estaria disposto os cartões no CAVALU da sala? Pregue os cartões no cartaz e discutam: O que é possível observar? Dispor os cartões no quadro ajuda a visualizar o número formado? Por quê?
- Qual é o número que o grupo deve compor?
Propósito: Compartilhar a resolução da atividade, propiciando a participação e interação dos alunos.
Sistematização do conceito

Tempo sugerido: 3 minutos.
Orientações: Ler a aprendizagem da aula e relacioná-la com as estratégias utilizadas pelos alunos para identificar o valor posicional dos algarismos em números e representá-los no quadro de pregas.
Propósito: Sistematizar o conceito principal aprendido na aula.
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes os conceitos estudados nessa aula.
Propósito: Resumir a aprendizagem da aula.
Raio X
Tempo sugerido: 8 minutos.
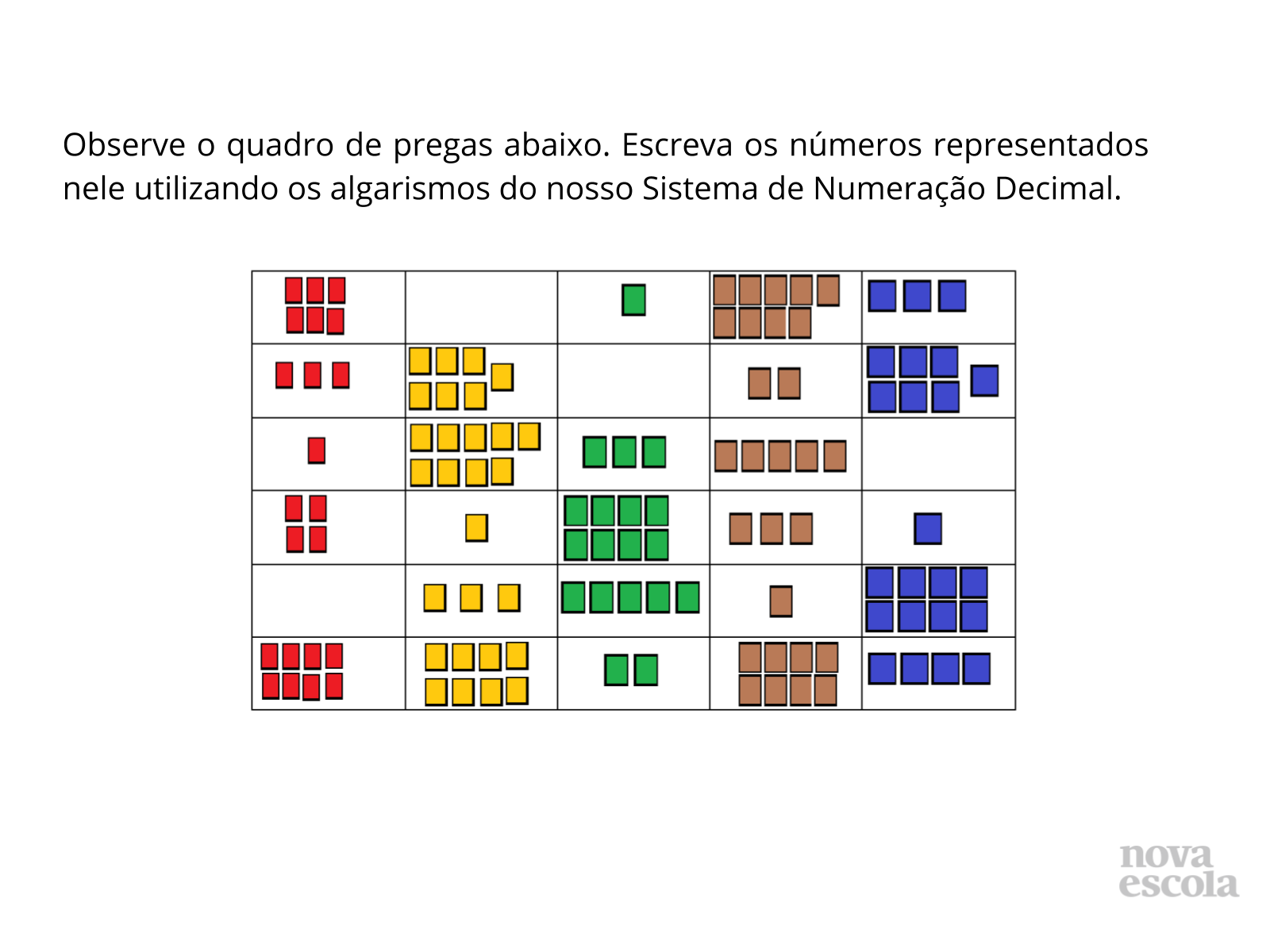
Orientações: Os alunos devem observar o quadro de pregas verificando o número de cartões e relacionando aos seus valores posicionais referentes. Questione às crianças a quanto se refere um cartão de cada cor. A partir da discussão dessas informações, solicite que escrevam os números representados em cada uma das linhas do quadro individualmente. O Raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Discuta com a turma:
- Qual o valor posicional de um cartão azul? E marrom? E verde? E amarelo? E vermelho?
- Se adicionarmos um cartão marrom no primeiro número o que acontecerá com os cartões verdes? Por quê?
- Como você faria para transformar o quinto número em 10 000?
- Como você leria cada um dos números?
- O que significa os espaços em branco no quadro? Que algarismo eles representam?
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da representação dos números do Sistema de Numeração Decimal, baseado no valor posicional de cada algarismo.
Materiais Complementares:
Resolução da Atividade Complementar
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_02NUM_01
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais)
- Opcionais: Google Documentos, Google Formulários, YouTube
Para este plano, foque na etapa Atividade Principal.
Aquecimento
Apresentar o quadro com os números presentes no slide, seguido das questões que estão nas orientações ao professor, no campo “Discuta com a turma”. Isso pode ser feito por escrito ou usando o Google Formulários, sem usar a pergunta que está no slide.
A devolutiva para os alunos precisa ser feita sempre baseada em perguntas que levem os alunos a pensarem sobre a situação, caso não tenham atingido o objetivo da atividade, ou seja, chegar ao número esperado.
Atividade principal
Propor diferentes organizações de cartões a serem distribuídas para os alunos e pedir que eles tentem listar a maior quantidade de números a serem formados usando os cartões coloridos. Você pode disponibilizar as imagens dos grupos de cartões (os 4 presentes na atividade e outros que você quiser criar) usando o Google Documentos, para que os alunos possam registrar os números formados por eles.
Caso a turma não tenha acesso à internet, você pode fornecer uma organização de cartões com desenhos diferentes que tenham valores distintos. Isso porque sabemos que xerocar atividades coloridas acaba ficando mais oneroso para enviar aos alunos.
Lembre-se de inserir em ambas situações as questões presentes nas orientações ao professor, no campo “Discuta com a turma”, para que os alunos possam refletir sobre sua prática enquanto organizam as possibilidades dos números a serem formados.
Discussão das soluções
Apresente o cartão a toda a turma, com uma lista de conclusões que foram tiradas a partir de uma análise de um grupo de alunos. Apresente cada um dos quatro cartões com as conclusões presentes nas falas das personagens que estão nos slides 4, 5, 6 e 7.
Para que os alunos possam fazer uma boa análise da situação, peça que eles mantenham atenção em alguns pontos específicos, destacados nas questões apresentadas nas orientações ao professor, no campo “Discuta com a turma”.
Os registros podem ser feitos no mesmo arquivo via Google Documentos utilizado na etapa anterior ou por escrito (lembrando que se houver troca das cores por imagens na etapa anterior isso também interfere nas resoluções propostas aqui).
Sistematização
O professor pode apresentar esta etapa a partir de um exemplo. Isso pode ser feito usando um vídeo curto no YouTube para mostrar como a posição dos algarismos interferem na decomposição do número.
Caso os alunos não tenham acesso à internet, o professor pode fornecer a sistematização em material impresso.
Encerramento
Pedir aos alunos que façam um resumo, em poucas palavras, no caderno o que aprenderam com as discussões desta aula.
Raio X
O professor pode propor a resolução da atividade desta etapa por escrito ou via Google Formulários, para facilitar a organização das respostas dadas, inclusive as devolutivas. Vale lembrar que se for feito o trabalho com atividade impressa, é importante cuidar da alteração das cores para imagens diferenciadas (em impressões preto e branco).
Convite às famílias
Convide a família a criar cartões junto com o aluno que representam as diferentes ordens. Em seguida, proponha que a família organize uma sequência de cartões para que os alunos possam responder qual o número formado. Dependendo do número de integrantes da família é possível até que os desafios sejam trocados entre eles, para promover a interação familiar.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Cíntia Diógenes
Mentora: Elisa Greenhalgh Vilalta
Revisora pedagógica: Eliane Zanin
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA02 - Mostrar, por decomposição e composição, que todo número natural pode ser escrito por meio de adições e multiplicações por potências de dez, para compreender o sistema de numeração decimal e desenvolver estratégias de cálculo.
Objetivos específicos
- Identificar o valor posicional dos algarismos representados nos números e representá-los no quadro de pregas;
- Compreender a função do zero na representação de números no Sistema de Numeração Decimal e utilizá-lo adequadamente.
Conceito-chave
Representação de números naturais utilizando seus valores posicionais.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Cartões coloridos;
- CAVALU (Cartaz de Valor de Lugar);
- Ábaco aberto;
- Projetor ( opcional).