Resumo da aula
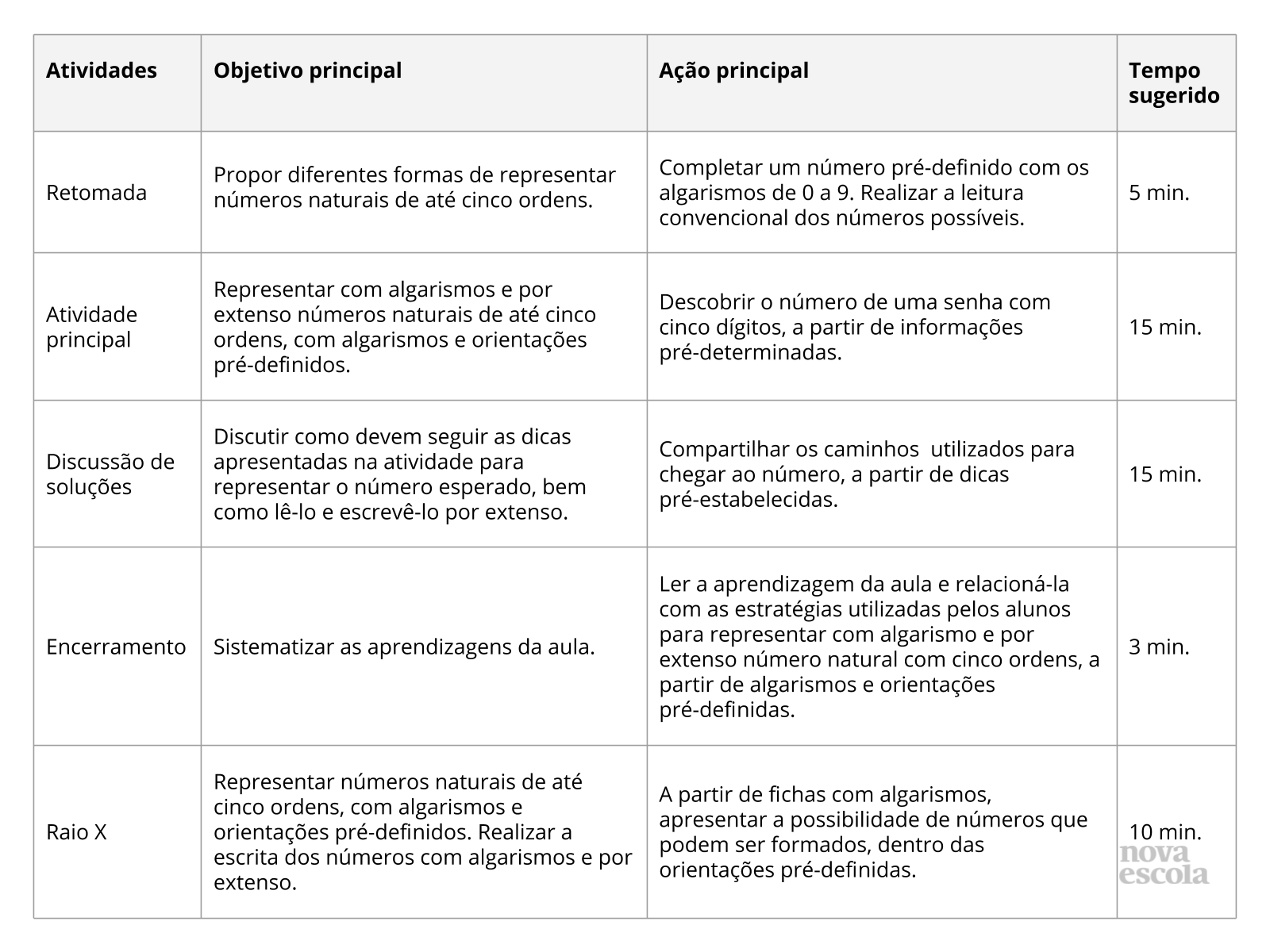
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo previsto: 5 minutos.
Orientações: Projete o slide ou escreva no quadro. Solicite que as crianças escrevam, em uma folha à parte, os números possíveis de serem formados a partir do que está sendo apresentado a elas. Após os alunos tentarem resolver individualmente, peça que eles comparem os números que eles conseguiram formar com os seus colegas, formando duplas ou trios para isso. As crianças devem compartilhar as estratégias de resolução desses problemas e suas hipóteses de como os números formados por elas devem ser lidos. Esteja atento ao envolvimento do grupo na atividade, mas, ao mesmo tempo, permita que as crianças interajam.
Propósito: Propor diferentes formas de representar números naturais de até cinco ordens.
Discuta com a turma:
- Quantos números podemos formar?
- Quais são eles?
- Como vocês chegaram a essa conclusão?
- Como vocês os leem?
Possíveis respostas:
O professor deve levantar uma discussão sobre quais as possibilidades de resposta para essa atividade, a partir do seguinte questionamento:
- Quais os algarismos possíveis de serem posicionados no espaço indicado?
Permita que as crianças apresentem suas hipóteses de resposta e realize o registro na lousa. No fim, peça que elas falem como leriam esses números. O professor deve discutir as respostas apresentadas pelos alunos, questionando como eles chegaram à essas conclusões.
93 054: Noventa e três mil e cinquenta e quatro.
93 154: Noventa e três mil, cento e cinquenta e quatro.
93 254: Noventa e três mil, duzentos e cinquenta e quatro.
93 354: Noventa e três mil, trezentos e cinquenta e quatro.
93 454: Noventa e três mil, quatrocentos e cinquenta e quatro.
93 554: Noventa e três mil, quinhentos e cinquenta e quatro.
93 654: Noventa e três mil, seiscentos e cinquenta e quatro.
93 754: Noventa e três mil, setecentos e cinquenta e quatro.
93 854: Noventa e três mil, oitocentos e cinquenta e quatro.
93 954: Noventa e três mil, novecentos e cinquenta e quatro.
Atividade principal
Tempo sugerido: 15 minutos.
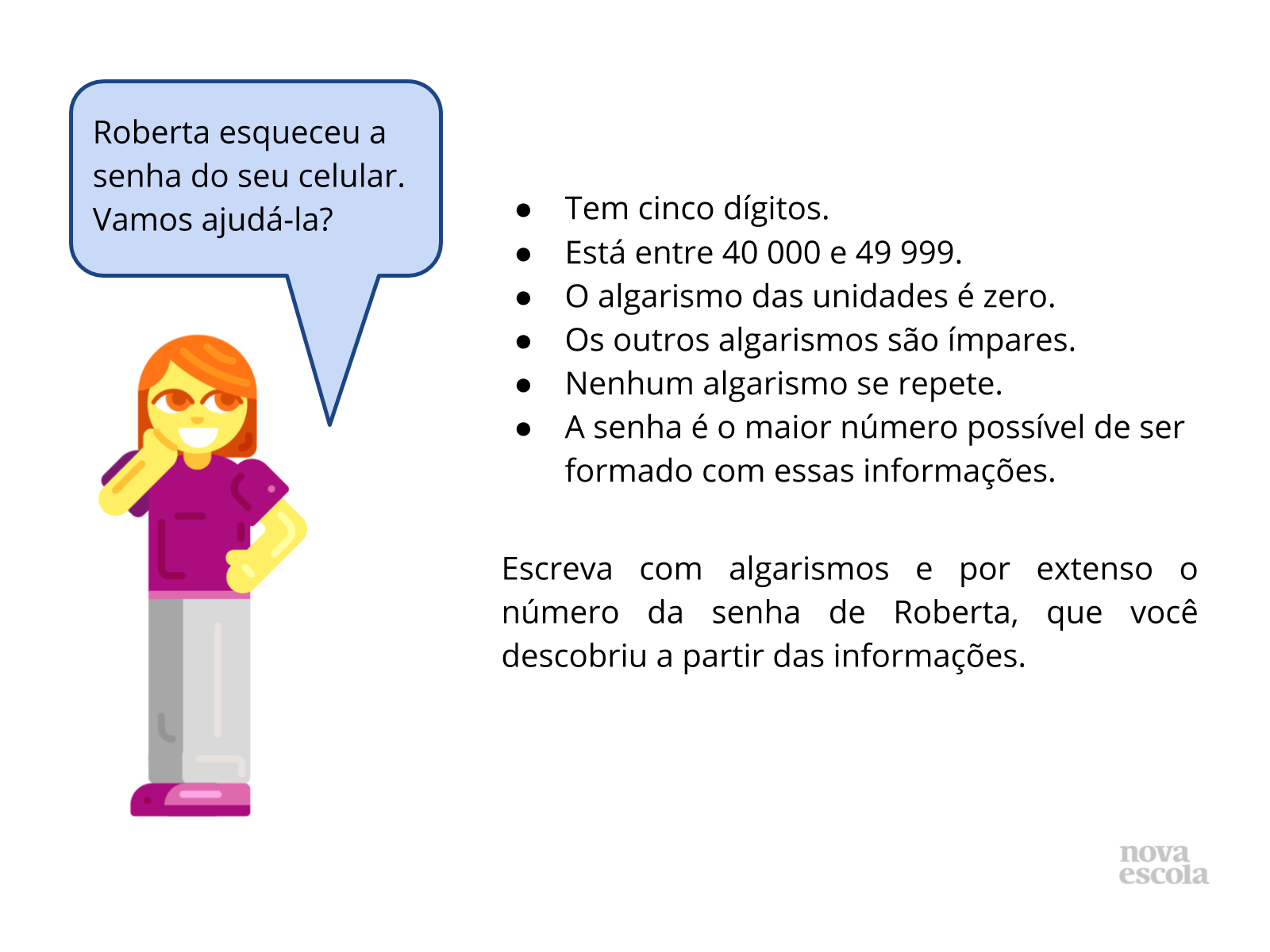
Orientações: Imprima e entregue para as crianças a situação problema. O professor deve disponibilizar para as crianças em torno de dois minutos para que elas leiam novamente o problema e reflitam sozinhas. Em seguida, divida a turma em grupos de três ou quatro crianças para discutirem a solução do problema. Peça que, nos grupos, eles proponham qual seria a senha de Roberta. Cada grupo deve então apresentar o caminho que eles fizeram para chegar ao resultado e qual seria ele. É importante que a fala de cada criança seja valorizada e esse não deve ser o momento para corrigir possíveis equívocos, mas discutir as estratégias dos grupos e verificar a contribuição de cada aluno para alcançarem uma resposta.
Utilize o guia de intervenções para refletir sobre as possíveis dificuldades ou os possíveis erros que as crianças podem apresentar ao tentar resolver a situação problema e quais intervenções o professor pode estabelecer para a promoção da aprendizagem da turma.
Propósito: Representar com algarismo e por extenso números naturais de até cinco ordens, com algarismos e orientações pré-definidos.
Discuta com a turma:
- Qual o primeiro passo que você daria para ajudar Roberta a relembrar a senha do seu celular?
- Como as dicas dadas por ela colaboram para descobrir o número da senha?
- Onde se localiza o algarismo das unidades no número?
- Qual deve ser o algarismo da ordem das dezenas de milhar? Qual a dica lhe ajudou a chegar a essa conclusão?
- Quais os algarismos que devem ser “encaixados” nos espaços que ainda não foram preenchidos no número? Por quê?
- De que forma você “encaixaria” esses algarismo?
- O que o levou a pensar assim?
- De acordo com as estratégias do seu grupo, qual o número da senha de Roberta?
- Como você leria o número da senha de Roberta?
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Como saber o que os alunos sabem sobre números
Fonte: https://novaescola.org.br/conteudo/6882/diagnostico-matematico-o-que-alunos-sabem-sobre-numeros.
Discussão de soluções

Tempo sugerido: 15 minutos.( slides 5 a 9 )
Orientações: Pergunte às crianças por onde elas começariam a resolução do problema. Apresentar as três estratégias escolhidas no slide e lançar as perguntas:
- Como você começaria a resolução do problema?
- Você faria parecido com os exemplos do slide ou usaria outra estratégia?
- Há alguma diferença entre posicionar primeiro o algarismo zero ou o algarismo 4? Como você explicaria sua opinião?
- Onde se localiza, no número, a ordem das unidades? E das dezenas dos milhares? Como você chegou a essa conclusão?
- Apresente para os seus colegas a sua estratégia.
Permita uma discussão sobre as hipóteses das crianças, disponibilize recursos para que elas apresentem concretamente (fichas, folhas de papel, pilot para quadro branco, giz…) como elas começariam a resolução da atividade. As intervenções do professor devem ter como finalidade possibilitar a participação dos alunos e não levar o aluno por um caminho de resolução pré-definido.
Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Discussão de soluções

Tempo sugerido: 15 minutos.( slides 5 a 9 )
Orientações: Permita que as crianças utilizem as fichas para dar continuidade à resolução da atividade, utilizando suas próprias estratégias. Se houver a oportunidade de, antecipadamente, produzir fichas de papel para que as crianças visualizem a formulação de suas hipóteses de resolução, seria bastante construtivo para o desenvolvimento da atividade. Nesse momento, possibilite a discussão e valorize a fala de cada aluno.
Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Discussão de soluções

Tempo sugerido: 15 minutos.( slides 5 a 9 )
Orientações: Peça para as crianças observarem a conclusão a que Cauê chegou no slide e questione as crianças:
- Você concordou com o Cauê?
- Baseado em quais dicas de Roberta ele chegou a esse resultado?
- Quais os algarismos que devem preencher as outras três fichas?
Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Discussão de soluções

Tempo sugerido: 15 minutos. ( slides 5 a 9 )
Orientações: Baseando-se na conclusão à qual Mariana chegou no slide, solicite que as crianças apresentem qual deve ser a estratégia que elas utilizariam para reconhecer o número que representa a senha do celular de Roberta.
- Quais as possibilidades de números que devem preencher as fichas vazias?
- Quantas fichas vazias há?
- Quais as dicas de Roberta que devem nortear as escolhas desses números?
- Em que ordem deve ficar os algarismos com maior valor absoluto?
- Quais os algarismos que devem ser posicionados nas outras ordens?
- Por que você fez essa escolha?
Abra espaço para a troca de ideias entre os alunos e valorize a participação de todos.
Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Discussão de soluções

Tempo sugerido: 15 minutos.( slides 5 a 9 )
Orientações: Discuta com a turma sobre o resultado ao qual as personagens chegaram nos slides.
Discuta com a turma:
- Você concorda com esse resultado?
- Esse é o único resultado possível? O que faz você pensar assim?
- Faria outro percurso para chegar a essa ou a outra resposta? Qual?
- Que informação limita o problema a uma resposta só?
- E se pudéssemos repetir os números ímpares, haveria uma só resposta também? Por quê?
- Por que os algarismos foram dispostos nessa ordem?
- Você saberia dizer qual o valor posicional de cada algarismo?
- Como lemos esse número?
- Utilizando os seus conhecimentos sobre o Sistema de Numeração Decimal, como escrevemos esse número?
Dê a oportunidade das crianças escreverem sua hipótese de escrita do número, sempre explorando o caminho trilhado por ela para chegar àquela escrita. Pedir que os alunos socializem suas escritas e compare-as, dando liberdade para que eles mesmos cheguem às próprias conclusões. Verifique se os alunos relacionam a escrita numérica, os valores posicionais dos algarismos e os seus conhecimentos prévios para realizar a escrita por extenso corretamente.
Resposta esperada:
49 750: Quarenta e nove mil, setecentos e cinquenta.
Propósito: Discutir a resolução da atividade, propiciando a participação e interação dos alunos.
Encerramento
Tempo sugerido: 3 minutos.
Propósito: Resuma a aprendizagem, revisando as estratégias utilizadas para a compreensão do assunto trabalhado.
Orientações: Retomar com os alunos os conceitos estudados nessa aula.
Raio X

Tempo sugerido: 10 minutos.
Orientações: Prepare e entregue os cartões para cada aluno. Esse material poderá ser utilizado pelas crianças como estratégia de resolução do problema. Estimule que os alunos façam tentativas e registrem os números encontrados individualmente. Em caso de dificuldade com a escrita do número, peça que a criança leia o número em voz alta e registre da forma como lê. Circule entre as mesas para verificar como os alunos estão resolvendo. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, individualmente, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da leitura e escrita de números naturais com cinco ordens e as diferentes formas de se representar números com os mesmos algarismos.
Discuta com a turma:
- Como vocês fizeram para representar os números?
- Quantos números diferentes vocês formaram? Que números foram esses?
- Como vocês leriam esses números?
- Como seria a escrita por extenso?
Materiais Complementares:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 


















