Resumo da aula
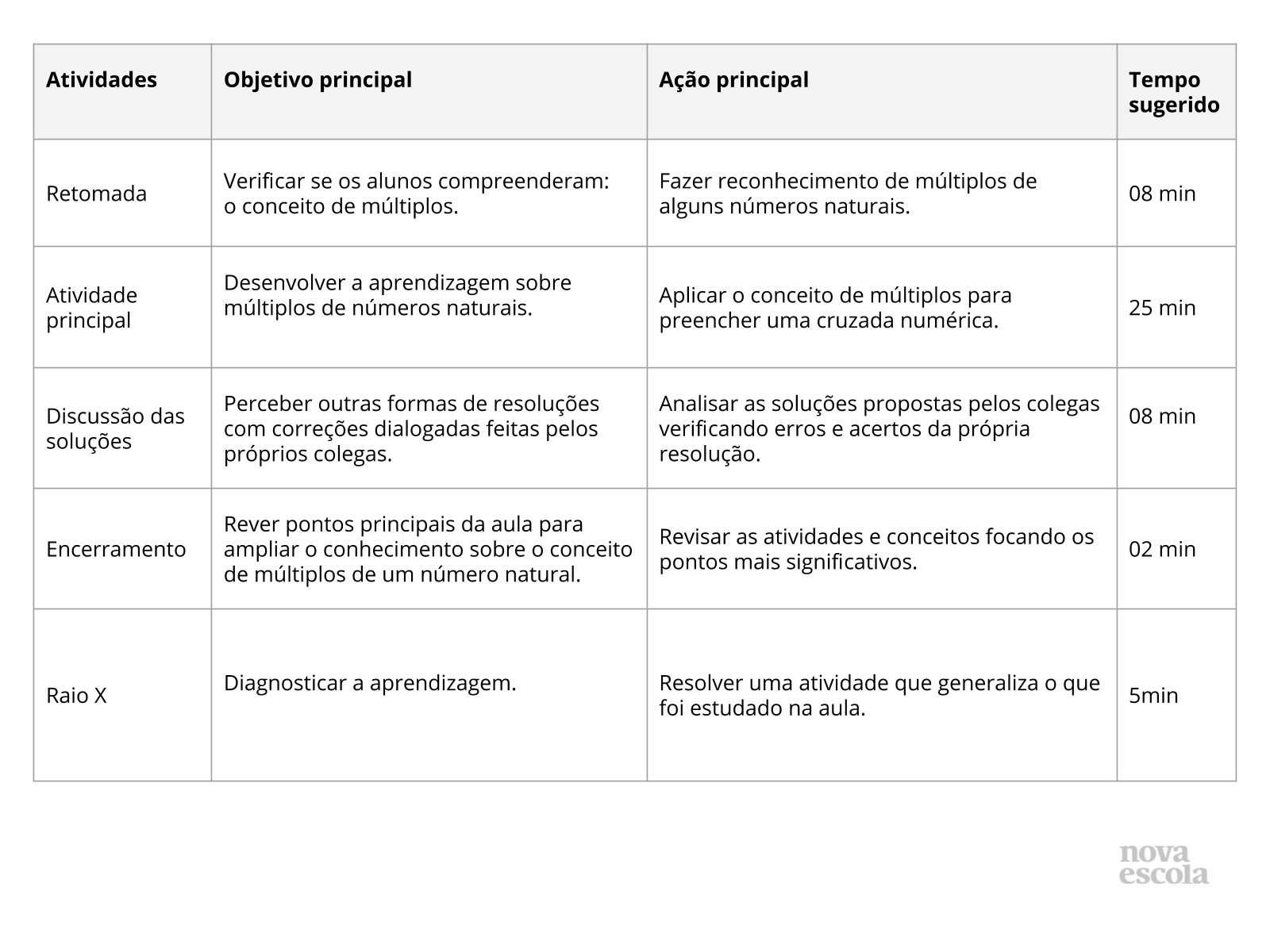
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 02 minutos
Orientações: Professor, leia para seus alunos o objetivo da aula.
Propósito: através do objetivo expresso, orientar os alunos sobre o que estudarão nesta aula.
Aquecimento

Tempo sugerido: 08 minutos.
Orientações: professor deixe seus alunos pensarem sobre a questão e trocarem ideias com seus colegas, depois oriente que eles devem registrar como pensaram, fazendo anotações no caderno.
Propósito: Perceber, através da resolução da atividade, que os números propostos para tomar os medicamentos possuem como múltiplo o número 24.
Discuta com a turma:
- Como você pensa em fazer a distribuição de horários?
- Se você fosse a mãe ou o pai de Elaine como você iria organizar os horários para dar os medicamentos a ela?
- Você consegue imaginar porque o médico escolheu esses números para intervalo de horários para os medicamentos, além da própria necessidade médica?
- O médico poderia ter receitado um medicamento que fosse de 5 em 5 horas?
- Por que o número 24 é importante nesta atividade?
- O que o número 24 é para os números 3, 4, 6 e 8?
- Materiais complementares:
Atividade aquecimento
Resolução do aquecimento
Atividade principal

Tempo sugerido: 25 minutos
Orientações: Organize a sala em grupos e apresente o problema. Uma atividade por grupo já é o suficiente, mas se puder imprimir mais, pode auxiliar os grupos a dividir tarefas.
Permita o uso da calculadora. Como o exercício depende da compreensão do significado de múltiplo, a calculadora pode ser uma ótima ferramenta para a verificação dos cálculos.
Leia com a sala todas as instruções para verificar se todos compreendem cada um dos desafios, e como preencher a cruzadinha. Pode ser que alguns alunos percebam a resposta imediata de alguns desafios como o item E (99), o item G (0) ou ainda o item (B) 555. Caso isso ocorra, utilize esses casos para exemplificar como as casas devem ser preenchidas e peça que os alunos justifiquem por que esses números satisfazem os desafios em questão.
Essa justificativa inicial para as primeiras descobertas é essencial para que eles comecem a mobilizar estratégias de resolução que se apliquem na continuidade do exercício.
Peça então que cada grupo se debruce sobre sua atividade visando chegar o mais longe que puder. Caso algum grupo termine antes dos outros, permita que os membros do grupo se distribuam entre os grupos restantes para auxiliar nas questões mais difíceis.
Propósito: Retomar o conceito de múltiplos estudado na aula anterior, aplicando o conhecimento para preencher corretamente a cruzadinha.
Discuta com a turma:
- Quantos algarismos tem cada um dos números procurados?
- 1000 é múltiplo de 6? Como você pode fazer para descobrir se 1000 é ou não múltiplo de 6?
- Como você pode descobrir um múltiplo de 6 maior do que 1000?
- Existe algum múltiplo de 3 e 5 que não seja múltiplo de 15?
- Existe algum múltiplo de 11 e de 17 que não seja múltiplo de 187?
- Quais são os números de 3 algarismos que resultam da multiplicação de um número por ele mesmo?
- Materiais complementares:
Atividade principal
Resolução da atividade principal
Guia de intervenções
Discussão de soluções

Tempo sugerido: 08 minutos
Orientações: Professor, estimule seus alunos a analisarem se a solução apresentada no slide está correta. Se algum aluno declarar que a solução não está correta, peça para ele explicar como pensou. É provável que ele mesmo perceba onde está errando e aprenda a forma correta. Deixe seus alunos apontarem novas ideias, pois há outros caminhos para resolver e essa troca de ideias é muito rica para o aprendizado de todos.
Propósito: Corrigir a atividade partindo de uma possibilidade de resolução.
Discuta com a turma:
- As ideias apresentadas pelas meninas no slide são interessantes, mas você pensou como elas? Explique para nós como você pensou.
- Você pensou em alguma forma diferente para começar a resolver a cruzadinha? E neste caso, como iríamos terminá-la?
Encerramento
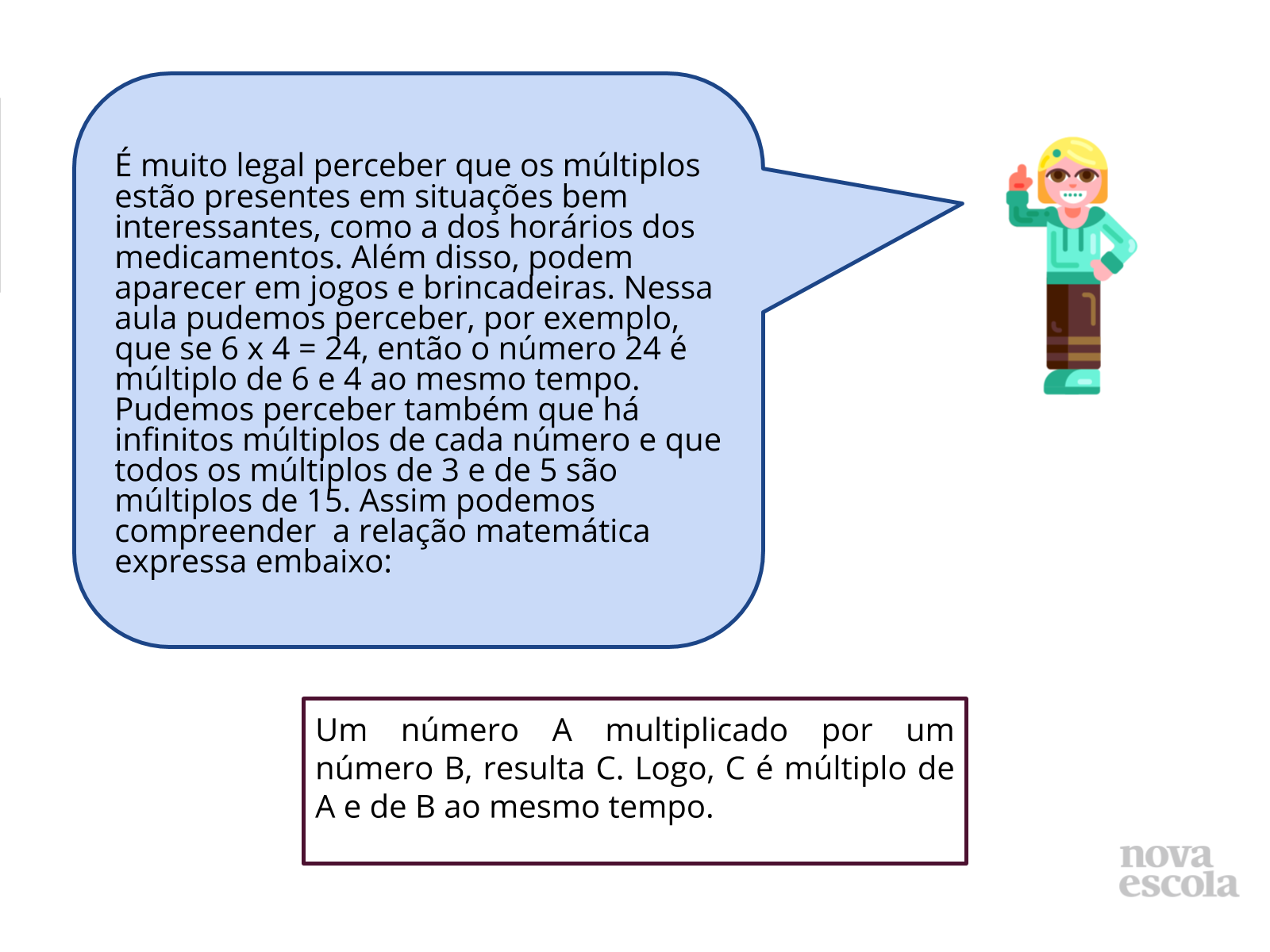
Tempo sugerido: 02 minutos
Orientações: Professor, peça para um aluno ler a fala da menina expressa no slide. Em seguida, você faz a leitura da relação matemática expressa abaixo. Depois, faça os questionamentos que estão no “discuta com a turma”.
Propósito: concluir o aprendizado desta aula destacando pontos importantes que foram estudados.
Discuta com a turma:
- Alguém poderia nos dar mais exemplos da relação matemática que aprendemos?
- Você consegue perceber essa relação matemática nas atividades que resolvemos nesta aula? Onde você percebeu?
- E no seu dia a dia, em que situações podemos aplicar essa relação matemática que estudamos hoje?



















