Guia de intervenções
Plano de Aula
Plano de aula: Códigos numéricos com base 10
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Uma nova ordem: dezena de milhar
Por: Cíntia Diógenes
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Cíntia Diógenes
Mentora: Elisa Greenhalgh Vilalta
Revisora pedagógica: Eliane Zanin
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA01 - Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.
Objetivos específicos
- Representar os números naturais de até cinco ordens;
- Ler e escrever números até 99999;
- Comparar os números naturais de até cinco ordens;
- Identificar padrões em sequências numéricas;
- Produzir um código de escrita numérica, diferente do usual, com base em sistema de numeração decimal.
Conceito-chave
Sistema de Numeração Decimal; Comparação de números naturais; Sequência numérica.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Projetor (opcional );
- Ábaco aberto.
Habilidades BNCC:
Objetivos de aprendizagem
- Representar os números naturais de até cinco ordens;
- Ler e escrever números até 99999;
- Comparar os números naturais de até cinco ordens;
- Identificar padrões em sequências numéricas;
- Produzir um código de escrita numérica, diferente do usual, com base em sistema de numeração decimal.
Resumo da aula
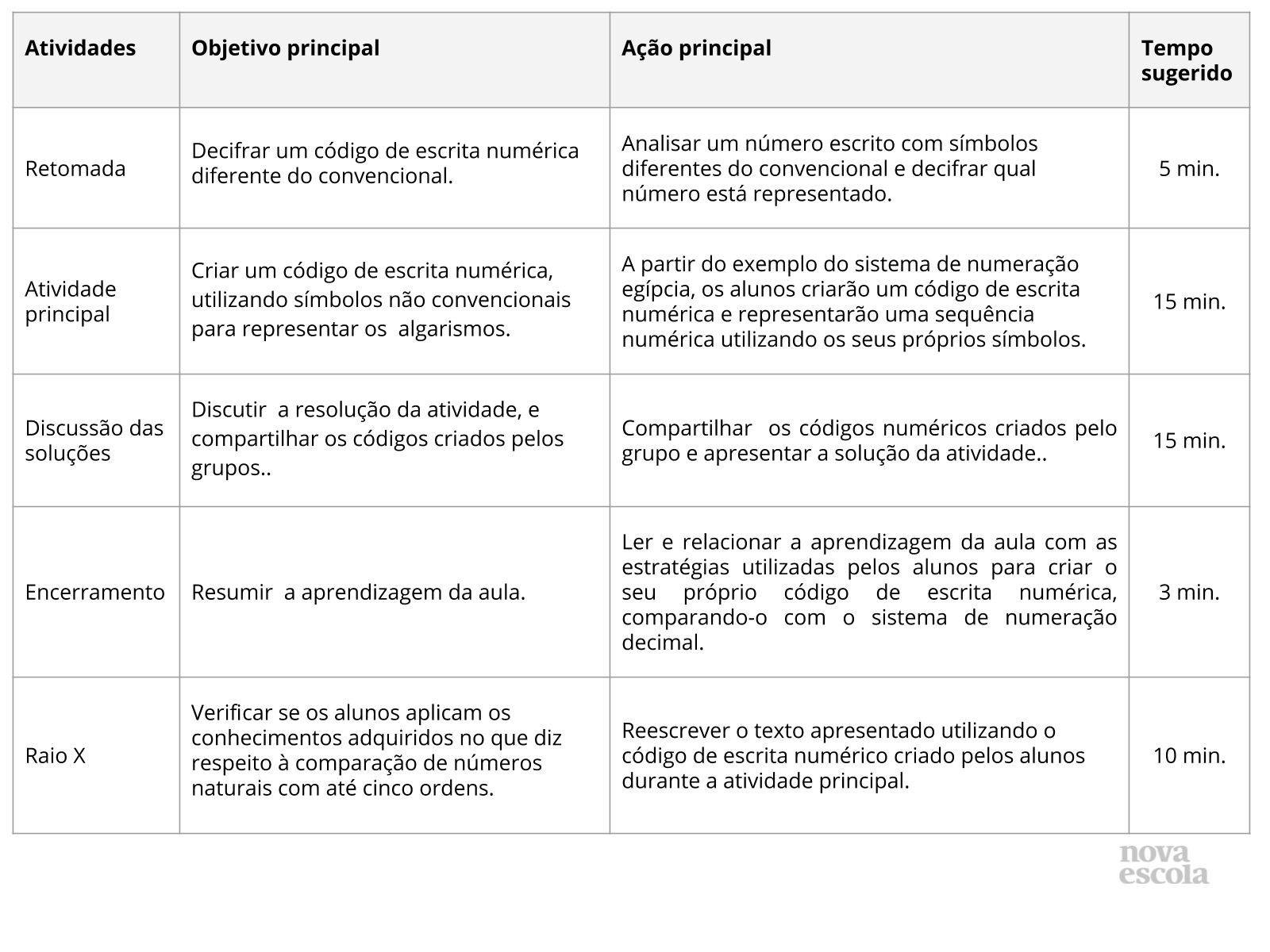 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

- Tempo sugerido: 2 minutos.
- Orientação: Projete ou leia o objetivo para a turma.
- Propósito: Compartilhar o objetivo da aula.
Retomada
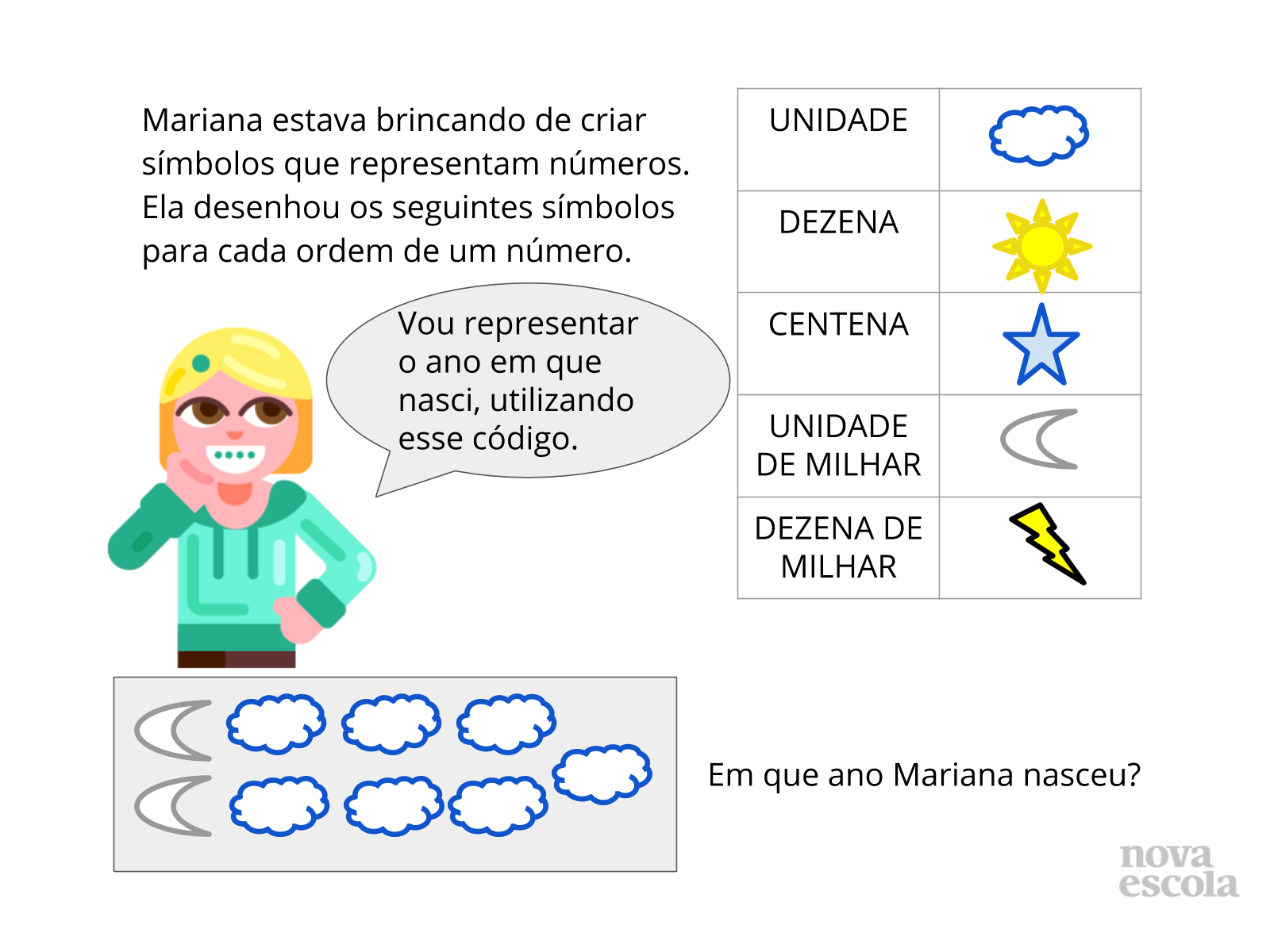
Tempo previsto: 5 minutos.
Orientações: Projete este slide ou escreva o conteúdo dele no quadro. Solicite que as crianças observem a tabela de símbolos criada por Mariana e expliquem oralmente como ela organizou o seu código de escrita numérica. Nesse momento, incentive a participação dos alunos valorizando a fala de cada um e intervindo com novos questionamento que os levem a refletir sobre o nosso sistema de numeração, comparando-o com o código de Mariana. Por fim, proponha que os alunos discutam em grupos de três ou quatro sobre qual teria sido o ano de nascimento de Mariana. Cada grupo deve compartilhar suas respostas com toda a sala, explicando como chegaram a essa conclusão.
Discuta com a turma:
- Quais ordens são representadas pelos símbolos criados por Mariana?
- Como seria a representação do número 4?
- Como você representaria o número 40, utilizando a menor quantidade de símbolos possíveis?
- Podemos representar o número 40 utilizando outro símbolo? Qual? Como seria essa representação?
- Como você representaria o número 400 utilizando a menor quantidade de símbolos possíveis? Podemos representar esse mesmo número utilizando outros símbolos? Quais? Como seria essa representação?
- Por que você acha que Mariana criou um novo símbolo para cada ordem? Esse sistema facilitou ou dificultou a representação do ano do seu nascimento?
- Em que ano Mariana nasceu?
- Por que, para representar o ano do seu nascimento, Mariana não fez uso de “sóis”, “estrelas” ou “raios”?
- Precisamos juntar quantas “nuvens” para termos um “sol”? Quantos “sóis” para termos uma “estrela”? Quantas “estrelas” para termos uma “lua”? Quantas “luas” para termos um “raio”?
- Quais semelhanças podemos verificar entre o código de escrita numérica que Mariana criou e o nosso sistema de numeração?
- E quais as diferenças entre eles?
- Como você representaria o número 44 444, utilizando a menor quantidade de símbolos possível do código criado por Mariana?
- Escreva o ano do seu nascimento, utilizando o código de Mariana.
Propósito: Decifrar um código de escrita numérica diferente do convencional.
Resposta esperada:
O ano que Mariana nasceu foi 2007.
Atividade principal

Tempo sugerido: 15 minutos.( slides 4 a 7)
Orientações: Peça que as crianças individualmente observem o sistema de numeração egípcio e reflitam sobre suas semelhanças e diferenças com o sistema de numeração que utilizamos em nosso dia a dia. Depois, peça que elas se reúnam em grupos de 4 ou 5 para discutirem acerca das suas observações. Fique atento para as colocações dos alunos, mediando a partir de novos questionamentos e permitindo a participação de todos. O desafio para os grupos é que eles criem um código de escrita numérica de base 10, assim como é o nosso. Esse deve ser um momento criativo e lúdico para os grupos. Peça para que eles criem um nome para o código que eles criaram, utilizem símbolos criativos, que não se assemelhem aos símbolos egípcios ou à atividade anteriormente proposta nesta aula. Permita que as crianças tenham um momento de trocas e que a sala seja envolvida por um barulho produtivo. A intervenção do professor deve ter como objetivo motivar as crianças a desenvolverem a atividade, induzindo a participação de todos e verificar se, para a produção do código, as crianças estão levando em consideração que os códigos devem partir da ideia de agrupamentos de base 10. Após os códigos criados, o professor deve solicitar que os alunos, em seus grupos, representem os números da sequência utilizando o código criado por eles. Quando todos tiverem finalizado essa etapa da atividade, discutir com os alunos qual o padrão verificado entre os números que fazem deles uma sequência numérica e qual seria o próximo número da sequência.
Você pode fazer o download desta atividade para imprimir para os seus alunos aqui.
Utilize o guia de intervenções para refletir sobre as possíveis dificuldades ou os possíveis erros que as crianças podem apresentar ao tentar resolver a situação problema e quais intervenções você pode estabelecer para a promoção da aprendizagem da turma.
Discuta com a turma:
- Quais números do nosso sistema de numeração os símbolos egípcios representam?
- Como você explicaria a representação do número 51 324 com símbolos egípcios?
- Qual o valor posicional do algarismo 5 no número 51 324?
- Para representar o algarismo cinco qual o símbolo utilizado? Quantas vezes ele foi desenhado? Por quê?
- Qual o valor posicional do algarismo 2 no número 51 324?
- Para representar o algarismo dois qual o símbolo utilizado? Quantas vezes ele foi desenhado? Por quê?
- A que conclusão você chegou sobre como representamos os números utilizando os símbolos egípcios?
- Para criar o seu código numérico, cada símbolo deve representar que número, respectivamente?
- Você consegue perceber o padrão na sequência numérica apresentada na atividade?
- Como você representaria cada número da sequência numérica da atividade utilizando os símbolos criados por você?
- Após representar os números utilizando o seu código de escrita numérica, foi mais fácil identificar o padrão da sequência?
- Que padrão é esse?
- Qual é o próximo número dessa sequência?
Propósito: Criar um código de escrita numérica, utilizando símbolos não convencionais para representar os algarismos.
Material Complementar:
Material complementar para o professor:
Conheça a história dos números.
Fonte:
http://www.ebc.com.br/infantil/voce-sabia/2015/05/conheca-historia-dos-numeros
Como agrupo meus alunos.
Fonte:
https://novaescola.org.br/conteudo/1475/como-agrupo-meus-alunos
As trocas que fazem a turma avançar
Fonte:
https://novaescola.org.br/conteudo/366/as-trocas-que-fazem-a-turma-avancar
Atividade principal

Tempo sugerido: 15 minutos.( slides 4 a 7)
Orientações: Esse será o momento em que você mediará a construção de um novo código de escrita numérica pelos alunos. Eles devem estar dispostos em grupos de quatro ou cinco crianças e criar coletivamente o seu código. Fique atento aos grupos, se estão levando em consideração que cada símbolo deve representar uma ordem do sistema de numeração decimal. Veja se existe lógica no código elaborado pelo grupo, se não há símbolos parecidos ou repetidos para representar cada ordem, então, além de circular pela sala, observe, se for necessário, interfira para que os símbolos criados por cada grupo obedeçam a lógica do sistema decimal, para depois dar prosseguimento à atividade. Para consertar a criação dos símbolos quando os alunos já estiverem trabalhando na representação dos números e na sequência será mais complicado. Além disso, medie esse momento, a fim de propiciar um ambiente criativo e permitindo a interação e participação de todos. Quando todos os grupos tiverem finalizado esse processo criativo, iremos para o próximo passo da atividade.
Propósito: Medira a resolução da atividade, propiciando a participação e interação dos alunos.
Discuta com a turma:
- Quais símbolos vocês escolheram em seu código para representar os números?
- Que número é representado por cada símbolo?
- Quais semelhanças você observa entre o seu código e o sistema de numeração decimal? E quais diferenças?
Atividade principal
Tempo sugerido: 15 minutos.( slides 4 a 7)
Orientações: Solicite que os grupos escrevam os dois primeiros números da sequência utilizando o código que criaram. Eles devem observar a diferença entre os dois números, a partir dos símbolos que foram incluídos ou retirados. É provável que eles verifiquem que o segundo número diferencia-se do primeiro por uma unidade e queiram generalizar essa situação para toda a continuidade da sequência. Porém, solicite que as crianças continuem escrevendo cada número da atividade. O padrão dessa sequência não é o acréscimo igual de uma quantidade entre um número e seu subsequente, mas uma determinada ordem sofre um aumento por número, por exemplo, do primeiro para o segundo acrescentamos uma unidade, já do segundo para o terceiro acrescentamos uma dezena, no próximo número verificamos o aumento de uma centena, e assim por diante. É importante que as crianças cheguem a essa conclusão após bastante discussão e reflexão, sendo importante a sua mediação de forma construtiva essa descoberta, a partir do levantamento de novos questionamentos e da observação.
Propósito: Mediar a resolução da atividade propiciando a participação e interação dos alunos.
Discuta com a turma:
- Quais os símbolos que vocês utilizaram para escrever os dois primeiros números da sequência?
- Quantas vezes vocês escreveram cada símbolo em cada um desses dois primeiros números?
- Qual a diferença que vocês observaram entre o primeiro e o segundo número?
- Olhando a sequência na atividade, você acredita que a diferença entre o primeiro e o segundo número é o padrão da sequência?
Atividade principal
Tempo sugerido: 15 minutos.( slides 4 a 7)
Orientações: Proponha aos alunos que escrevam o terceiro número da sequência utilizando o código que o grupo criou. Esse deve ser um trabalho colaborativo, por isso fique atento para perceber se todos os membros do grupo estão participando ativamente da resolução da atividade. Após a escrita do terceiro número, os alunos perceberão que não foi acrescentado uma unidade ao número subsequente, mas uma dezena. É possível que eles argumentem haver um erro na sequência. Proponha que o grupo dê continuidade à escrita da sequência e tire suas conclusões a partir do que eles irão observar. Observando a escrita do quarto e do quinto número é provável que as crianças percebam que a cada novo número cada ordem sofre o acréscimo de uma mesma quantidade. Portanto, no quarto número é acrescentado uma centena ao número antecedente. Já no quinto número é acrescentado uma unidade de milhar.
Propósito: Mediar a resolução da atividade, propiciando a participação e interação dos alunos.
Discuta com a turma:
- Ao escrever o terceiro número, o que você observou? Houve algo que o seu grupo considerou estranho?
- Seu grupo está enfrentando alguma dificuldade nessa atividade? Explique.
- Já é possível verificar o padrão dessa sequência?
Discussão de soluções

Tempo sugerido: 15 minutos.
Orientações: Após a escrita de todos os números, os grupos apresentarão a quais conclusões chegaram durante a atividade, quais estratégias utilizaram para verificarem o padrão da sequência e como foi a construção do código que criaram. Seria interessante que os códigos de cada grupo ficassem expostos na sala, para posteriormente a turma retomar a ideia, quando forem trabalhar a composição e a decomposição dos números naturais. Ao final, coletivamente, pergunte à turma qual é o próximo número da sequência.
Propósito: Compartilhar a resolução da atividade, propiciando a participação e interação dos alunos.
Discuta com a turma:
- Quais as maiores dificuldades enfrentadas pelo grupo para escrever os números da sequência? E para descobrir o padrão?
- Quais as semelhanças e diferenças entre o código criado pelo seu grupo e os outros?
- Como seu grupo chegou à conclusão de qual é o padrão da sequência?
- Partindo das suas descobertas, qual é o próximo número dessa sequência? Como vocês chegaram a essa conclusão?
Material Complementar:
Resolução da Atividade Principal
Encerramento
- Tempo sugerido: 3 minutos.
- Orientações: Encerre a atividade retomando com os estudantes os conceitos estudados nesta aula.
- Propósito: Resumir a aprendizagem da aula.
Raio X

Tempo sugerido: 10 minutos.
Orientações: As crianças irão utilizar o código numérico que eles mesmos criaram durante a atividade principal desse plano de aula, baseado no sistema de numeração de base 10. A atividade Raio-X deve ser realizada individualmente, portanto, cada aluno deve ter a cópia dos símbolos que seu grupo criou. Peça que a turma se atente para os valores descritos no texto, para reescrevê-lo, substituindo os números escritos com o código numérico convencional do nosso sistema de numeração pelos símbolos que eles criaram na aula. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções na lousa. Você pode fazer o download desta atividade para imprimir para os seus alunos.
Discuta com a turma:
- Como lemos esses números?
- Qual o valor posicional de cada número?
- Por que a pessoa não poderia comprar o carro, mesmo com o desconto dado pelo vendedor?
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_01NUM_05
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: -
- Opcionais: Jamboard, Google Apresentações, Google Meet, Google Formulários.
Para este plano, foque na etapa Atividade Principal.
Retomada
O professor pode organizar as figuras do slide em uma tela do Jamboard e discutir com a turma sobre a organização dos números via Google Meet. Caso não seja possível usar a internet, é possível entregar impresso aos alunos.
Atividade principal
O professor pode organizar slides com o Google Apresentações mostrando como funciona o sistema de numeração egípcio, disponibilizando uma tela para cada aluno trabalhar com seu próprio Jamboard, experimentando a montagem do número que quiser, socializando com a turma via Google Meet. Caso não seja possível usar a internet, é possível entregar impresso aos alunos e pedir que redijam suas explicações sobre o posicionamento dos símbolos.
O mesmo movimento pode ser feito em relação à criação dos sistemas de numeração por parte dos alunos.
Discussão das soluções
Os alunos podem socializar suas criações via Google Meet ou enviando um arquivo pelo Google Formulários contendo os símbolos criados e a explicação sobre o mesmo.
Sistematização
Não há.
Encerramento
Pedir que os alunos escrevam uma lista de vantagens do nosso sistema de numeração (SND) em relação ao sistema de numeração criado por eles (isso pode ser feito com o Google Formulários ou por escrito).
Raio X
Propor aos alunos a escrita de outro valor com os mesmos algarismos do preço com desconto que ainda assim não permitam ao cliente comprar o carro. O registro pode ser feito por escrito ou via Google Formulários.
Convite às famílias
Propor às famílias uma pesquisa sobre valores de automóveis que tenham sua faixa de preço indicado com 5 dígitos para comparação dos valores (maior, menor, escrita em ordem crescente), além de pedir que eles identifiquem valores que apresentem um mesmo algarismo com valor diferente (por exemplo: o algarismo 4 nos números 34 987 e 42 567).
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Cíntia Diógenes
Mentora: Elisa Greenhalgh Vilalta
Revisora pedagógica: Eliane Zanin
Especialista de área: Luciana Tenuta
Habilidade da BNCC
EF04MA01 - Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.
Objetivos específicos
- Representar os números naturais de até cinco ordens;
- Ler e escrever números até 99999;
- Comparar os números naturais de até cinco ordens;
- Identificar padrões em sequências numéricas;
- Produzir um código de escrita numérica, diferente do usual, com base em sistema de numeração decimal.
Conceito-chave
Sistema de Numeração Decimal; Comparação de números naturais; Sequência numérica.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Projetor (opcional );
- Ábaco aberto.









