Resumo da aula
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 3 minutos.
Orientações: Este é um momento de mobilizar questionamentos dos alunos sobre as relações entre as resoluções geométrica e algébrica. Pergunte a eles quais as maneiras como essas resoluções se relacionem. Valorize as hipóteses e estimule que os alunos busquem verificar as validades dessas hipóteses na resolução da atividade principal.
Propósito: Mobilizar a discussão sobre o assunto e estimular a curiosidade dos alunos.
Atividade principal

Tempo sugerido: 10 minutos.
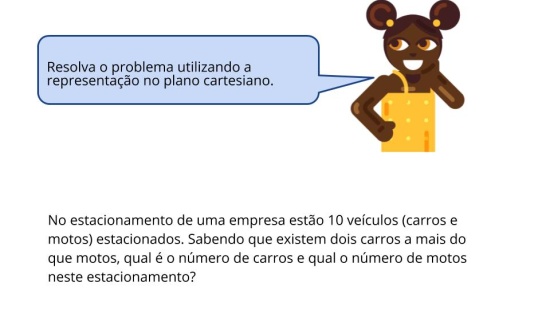
Orientação: Sugira que os alunos façam uma exploração livre da representação no plano cartesiano. Se eles tiverem dificuldade em fazer uma exploração de como poderia ser a representação no plano, sugira que eles encontrem uma equação que represente a situação. A partir da equação, oriente-os a resolver substituindo valores em uma tabela para, então, traçar o gráfico. Em seguida, peça para eles resolverem algebricamente o problema utilizando a estratégia que eles se sentem mais à vontade.
Propósito: Resolver a situação problema utilizando uma estratégia algébrica e uma estratégia geométrica.
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão das soluções

Tempo sugerido: 22 minutos. (slides 5 a 10)
Orientações: Apresentar a triangulação entre representação algébrica, em formato de tabela para, enfim, obter uma representação geométrica é interessante. Essa tabela pode ser feita coletivamente no quadro. É importante que eles percebam que não é necessário mais do que dois pontos e que a escolha desses pontos pode facilitar na representação do gráfico. Porém, como este não é o objetivo principal, não tem necessidade de dar muita ênfase nesse sentido.
Propósito: Representar a situação por meio de um sistema de equações do primeiro grau.
Discussão das soluções
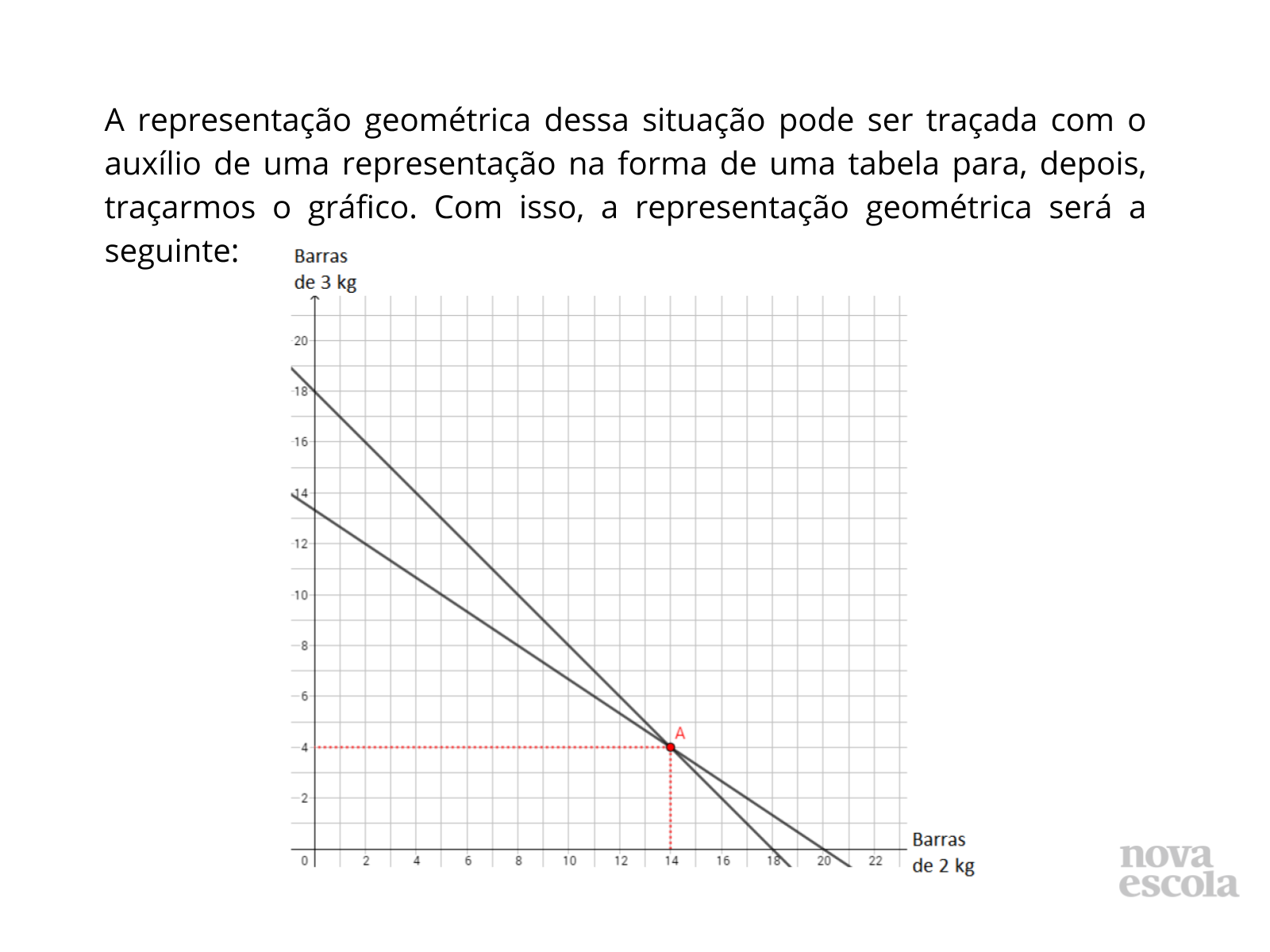
Tempo sugerido: 22 minutos. (slides 5 a 10)
Orientações: Elabore as tabelas para auxiliar a determinação das representações geométricas de cada uma das equações.
Propósito: Determinar a representação geométrica da situação problema.
Discussão das soluções

Tempo sugerido: 22 minutos. (slides 5 a 10)
Orientações: Resolver o sistema a partir de sua representação algébrica. É interessante que você selecione dois alunos que tenham resolvido o sistema a partir das duas estratégias apresentadas. Caso haja algum erro na resolução dos alunos, aproveite esse momento para retomar conceitos já comentados.
Propósito: Resolver o problema algebricamente.
Discussão das soluções

Tempo sugerido: 22 minutos. (slides 5 a 10)
Orientações: Retomar as equações tais como ficaram depois da sua manipulação para verificar sua nova representação geométrica.
Propósito: Revisitar a nova equação encontrada a partir da substituição de uma equação em outra.
Discussão das soluções
Tempo sugerido: 22 minutos. (slides 5 a 10)
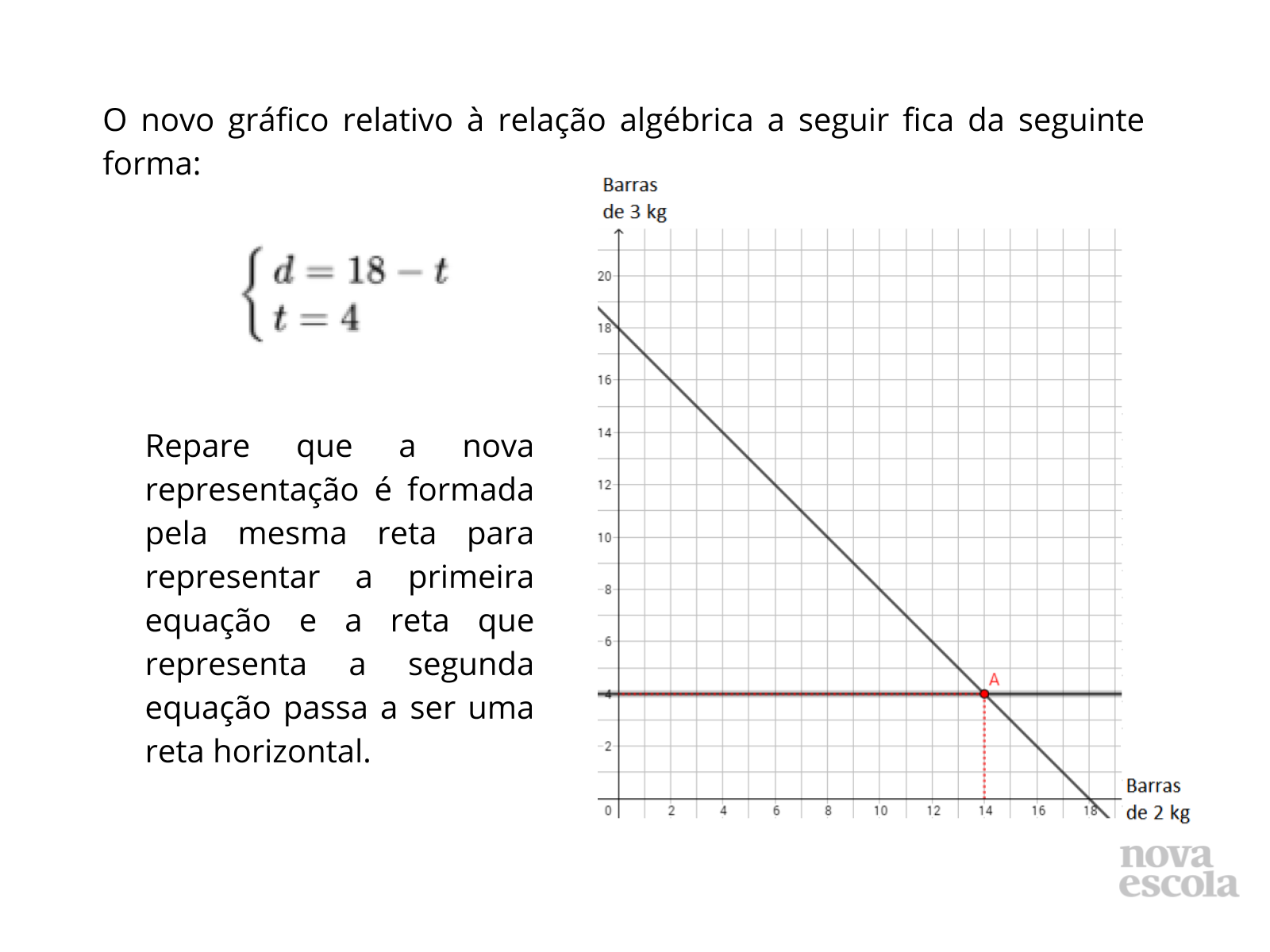
Orientações: Pode ser complicado o aluno compreender que uma equação do tipo t=4 será uma reta perpendicular à reta que representa esta variável. Antes de apresentar esta representação, busque que essa seja uma resposta vinda dos alunos. Discuta com eles o que pode representar esta situação.
Propósito: Representar o novo sistema encontrado a partir da sua representação geométrica.
Discussão das soluções
Tempo sugerido: 22 minutos. (slides 5 a 10)
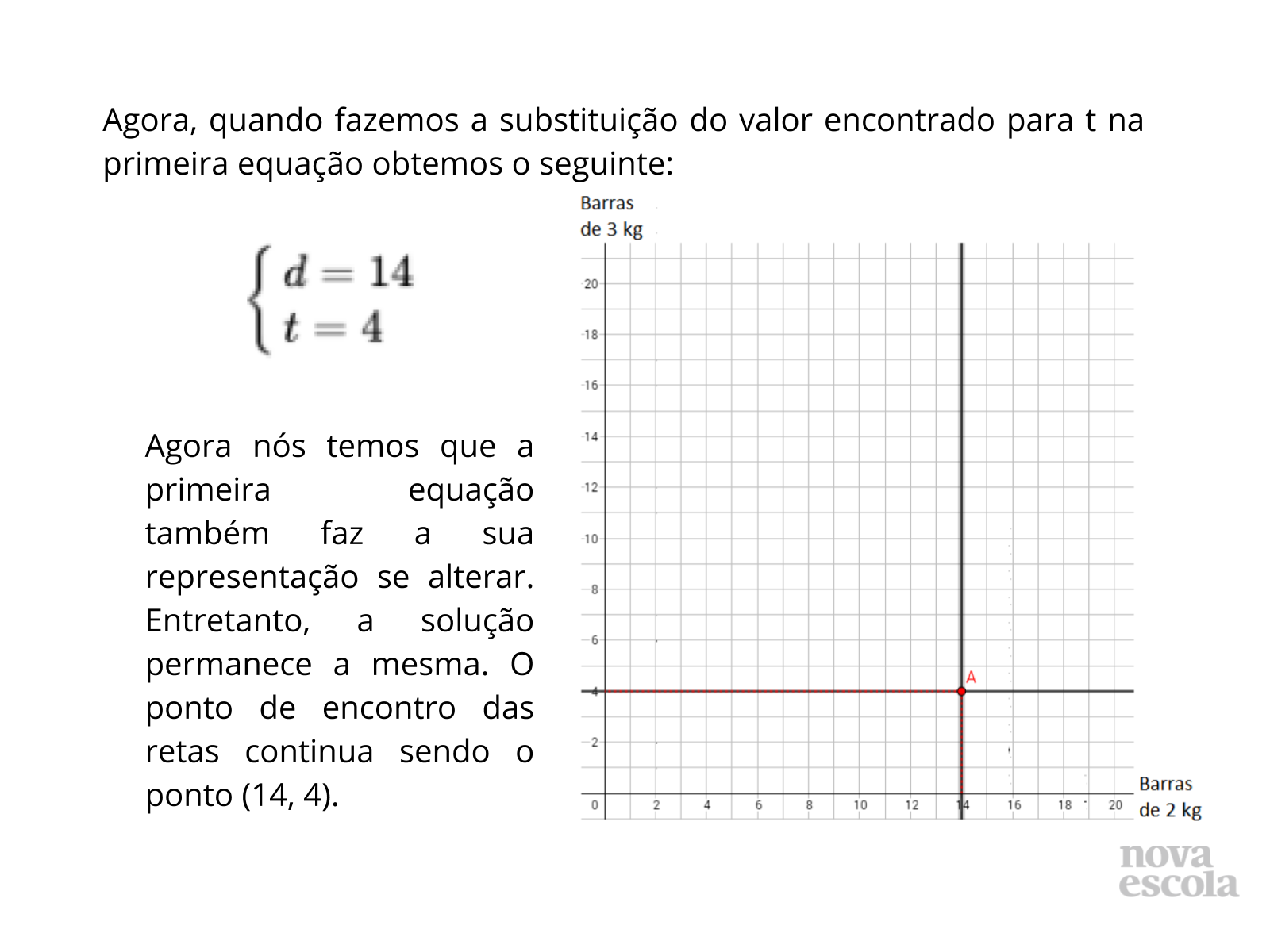
Orientações: Aqui novamente vai aparecer a representação de uma reta perpendicular ao eixo a qual representa a incógnita.
Propósito: Representar o novo sistema encontrado a partir da sua representação geométrica.
Encerramento

Tempo sugerido: 3 minutos. (slides 11 e 12)
Orientações: Esse é um momento de sintetização e formalização do conteúdo visto na aula de hoje. Busque uma frase de fechamento a partir das falas dos alunos. Não deixe de fazer o registro escrito pois esse é um momento de produção dos alunos.
Propósito: Apresentar um conjunto de conclusões a partir da discussão das soluções.
Encerramento

Tempo sugerido: 3 minutos. (slides 11 e 12)
Orientações: Essa parte da aula precisa ser compreendida como um momento de sistematização do conteúdo. Por isso, sugerimos que este seria um momento onde pode e deve ser feito algum tipo de registro escrito do que foi aprendido ao longo da aula.
Propósito: Sistematizar o conteúdo apresentado.
Raio X

Tempo sugerido: 10 minutos.
Orientações: Permita que os alunos resolvam as questões a partir da estratégia algébrica que eles preferirem. Sugerimos que a atividade seja feita em dupla para promover discussões pertinentes. Lembre os alunos que este problema deve ser resolvido a partir das estratégias algébrica e geométrica em paralelo.
Propósito: Avaliar o conteúdo discutido durante a aula.
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar