Atividade principal
Plano de Aula
Plano de aula: Sistema de Equações Lineares (Ampliação)
Plano 3 de uma sequência de 5 planos. Veja todos os planos sobre Resolução de equações e sistema de equações lineares
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Habilidade da BNCC
EF08MA08 - Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
Objetivos específicos
- Resolver um sistema de equações lineares com duas incógnitas.
- Utilizar o método da adição para determinar a solução de um problema modelado a partir de um sistema de equações.
Conceito-chave
Solução de um Sistema de Equações Lineares.
Recursos necessários
Lápis, borracha, caderno.
Habilidades BNCC:
Objetivos de aprendizagem
- Resolver um sistema de equações lineares com duas incógnitas.
- Utilizar o método da adição para determinar a solução de um problema modelado a partir de um sistema de equações.
Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Aula
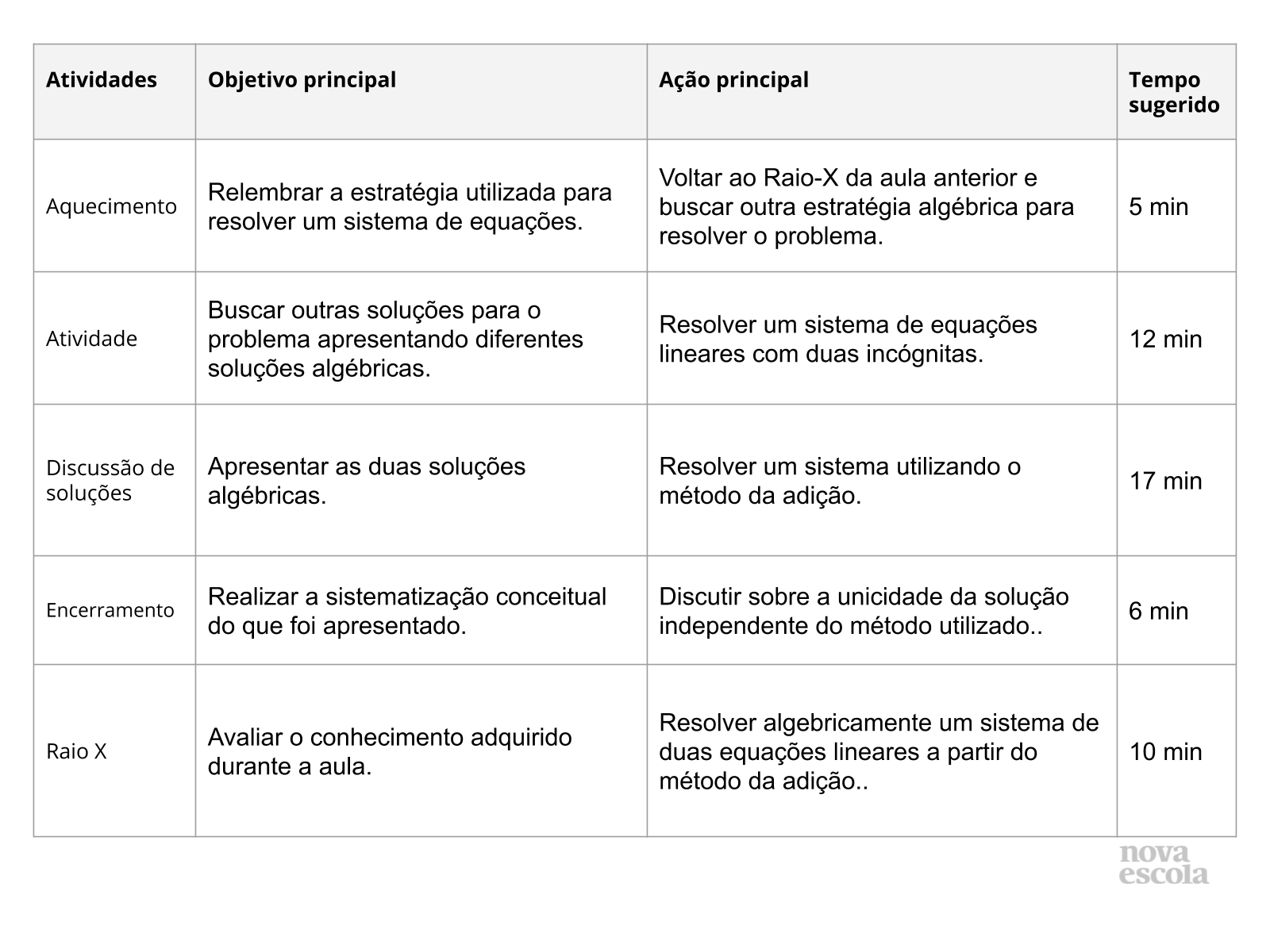
Resumo da aula
Orientações:Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão. Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
Tempo sugerido: 1 minuto.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Novo curso gratuito
Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO
