Resolução das atividades
Plano de Aula
Plano de aula: Programando um polígono regular
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Fluxogramas para a construção de polígonos
Descrição
Sobre o plano - MAT9_27GEO05 / Programando um polígono regular?!
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Fabricio Eduardo Ferreira.
Mentor: Rodrigo Morozetti Blanco
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
- Familiarizar o aluno com a simbologia utilizada na elaboração de um fluxograma;
- Calcular o valor de um ângulo externo a partir da medida de seu suplemento (ângulo interno);
- Determinar o valor da medida de um ângulo externo a partir da soma dos ângulos externos de um polígono regular;
- Descrever por meio de um fluxograma os passos para a obtenção de um polígono regular.
Habilidades BNCC:
Objetivos de aprendizagem
- Familiarizar o aluno com a simbologia utilizada na elaboração de um fluxograma;
- Calcular o valor de um ângulo externo a partir da medida de seu suplemento (ângulo interno);
- Determinar o valor da medida de um ângulo externo a partir da soma dos ângulos externos de um polígono regular;
- Descrever por meio de um fluxograma os passos para a obtenção de um polígono regular.
Resumo da aula
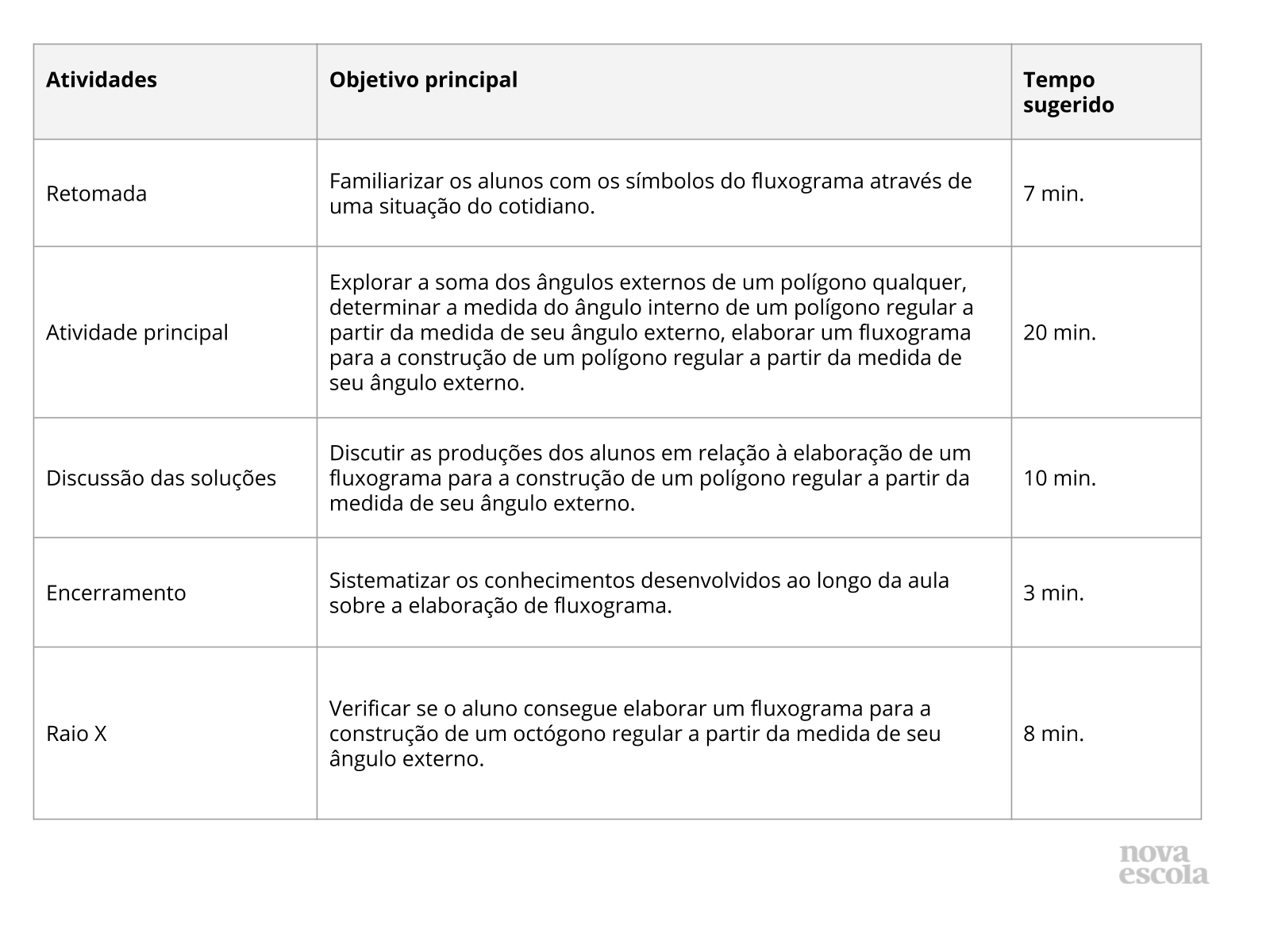
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão. O tempo sugerido prevê 48 minutos de atividade e 2 minutos para compartilhar com a turma o objetivo da aula.
Objetivo

Tempo sugerido: 2 minutos
Orientações:
Compartilhe com a turma o objetivo da aula lendo-o em voz alta, projetando-o (se estiver fazendo uso de apresentação de slides) ou escrevendo-o no quadro.
Retomada
Tempo sugerido: 7 minutos (slides 3 e 4)
Orientações:
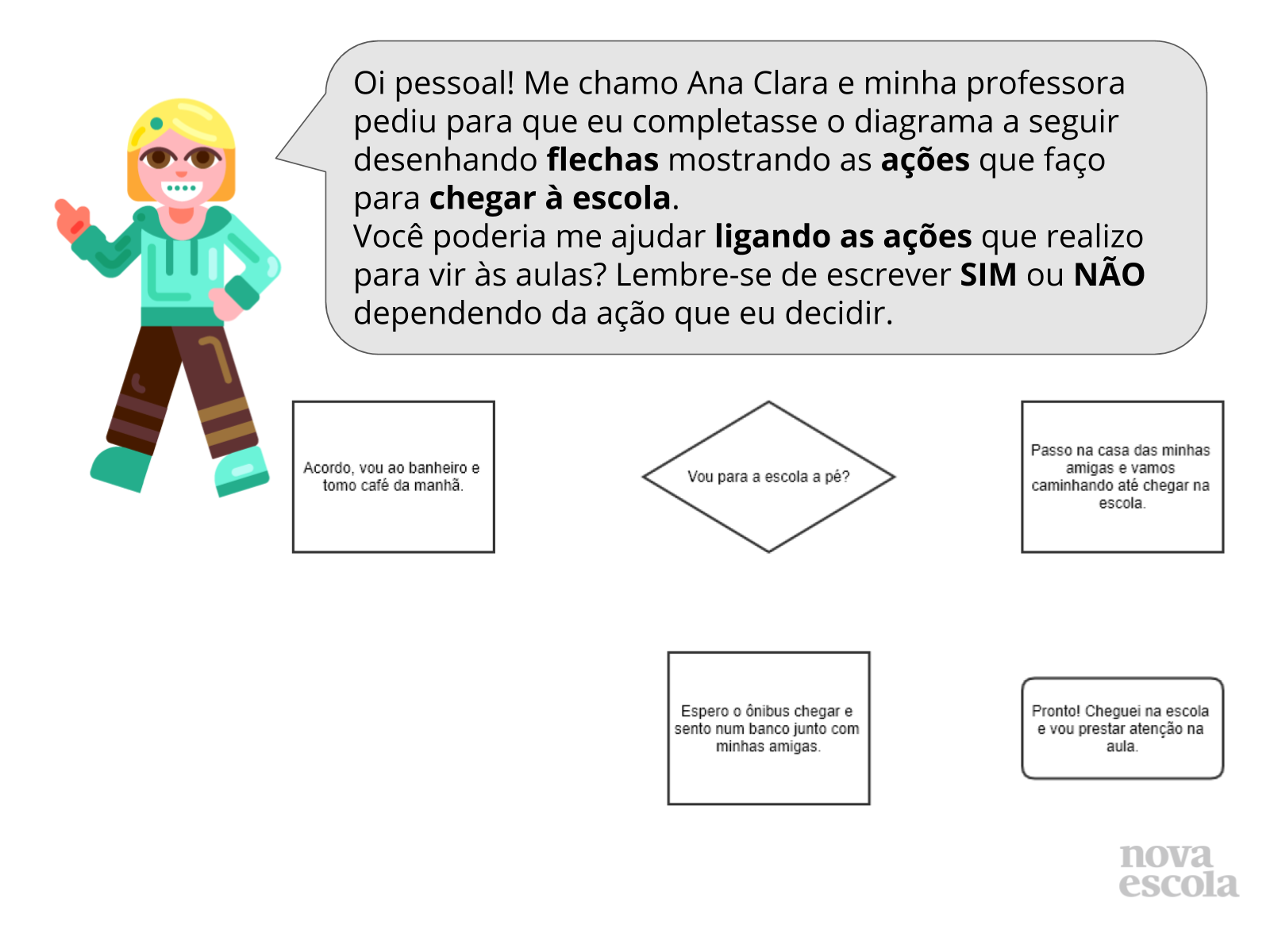
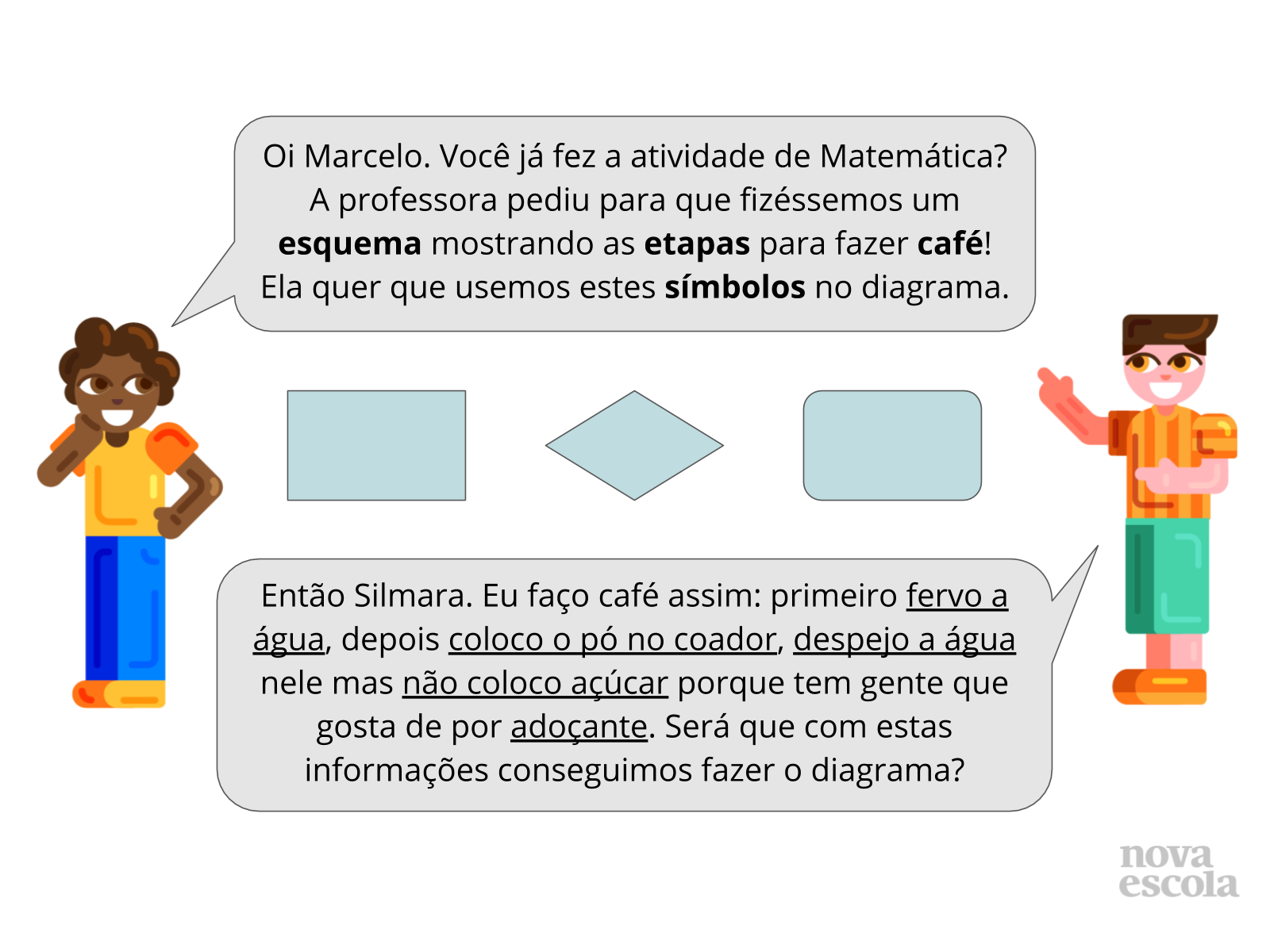
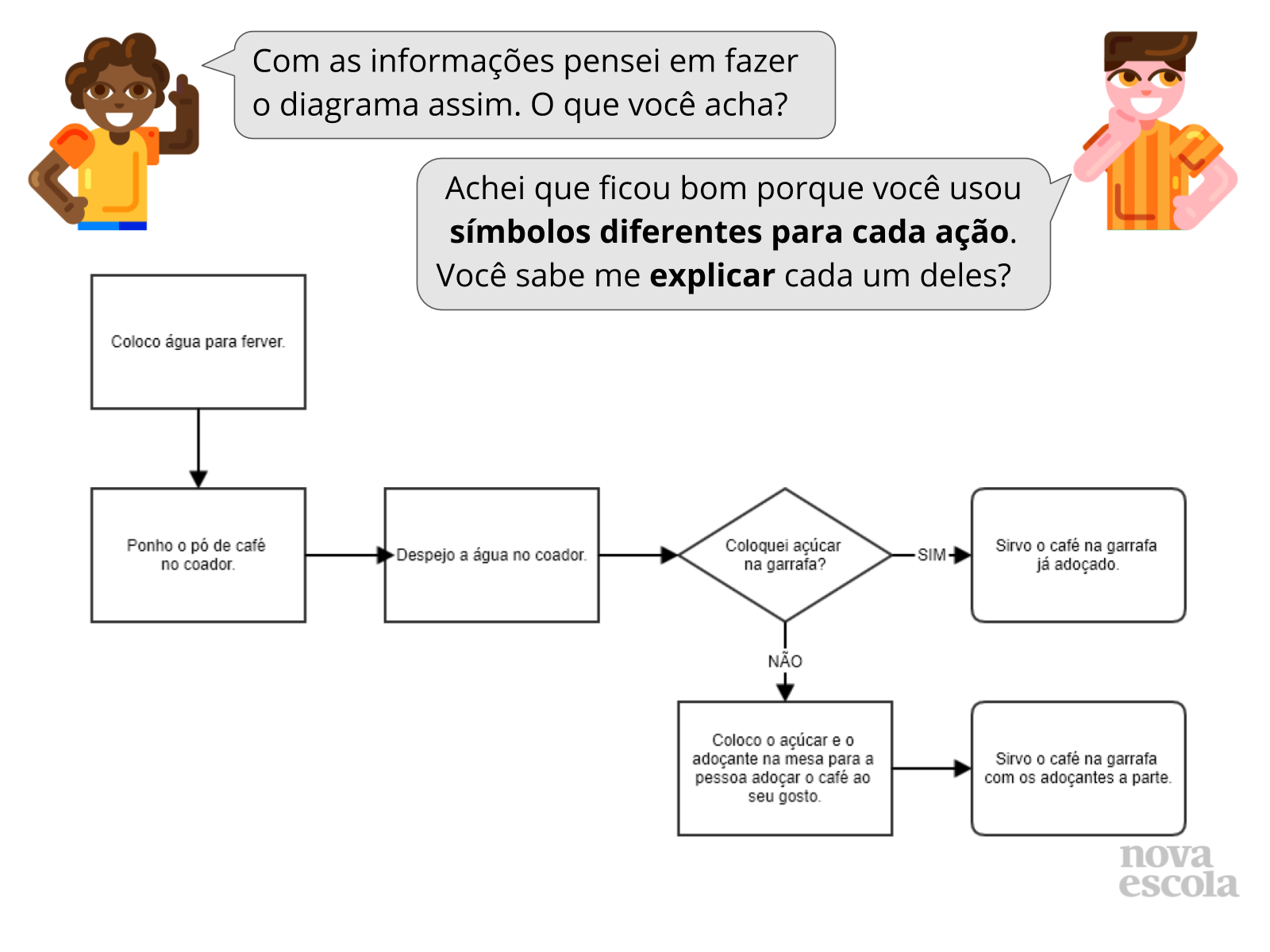
Inicialmente forme duplas com os alunos onde pelo menos um deles saiba preparar café. Peça para que um dos alunos leia o primeiro balão de fala da personagem e que o outro membro da dupla leia o segundo balão do outro personagem. Dê alguns minutos para que os alunos discutam como eles preparam o café e como elaborar um fluxograma mostrando as etapas do preparo. Peça para que os alunos fiquem atento ao tipo de símbolo utilizado de acordo com a ação executada e questione os mesmos sobre colocar ou não açúcar no café.
Depois que o fluxograma estiver pronto peça para que uma das duplas explique para os demais como elaboraram e a função de cada símbolo nele. O retângulo é destinado às ações a serem executadas, o losango para a tomada de decisões e o símbolo com cantos arredondados para o final do processo. Você pode utilizar o fluxograma do slide 4 para auxiliar na validação das produções dos alunos.
Propósito:
Familiarizar os alunos com os símbolos de um fluxograma e suas funções.
Discuta com a turma:
- Conte um para o outro como vocês preparam café em suas casas? Qual é a primeira coisa a ser feita? E depois?
- Todos costumam adoçar o café ou existe a possibilidade de adoçar depois? Como você indicaria isto em seu diagrama?
- Observando o diagrama do slide 4 tente descobrir a diferença entre as funções de cada símbolo.
Materiais complementares:
Atividade Retomada para impressão: https://nova-escola-producao.s3.amazonaws.com/TsZJDS7GYPzK27WkEpXHb9uh5gMfzWj858yDT65FNgq2Xfa7vCn9xyDKTBPt/atividade-retomada-mat9-27geo05.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/CV3euEQE9WP6GPMeQGM3ggG3bQBtZc6tGQFxVwm2Qv6CZcdQ8w7E2n3WUqKE/resolucao-das-atividades-mat9-27geo05.pdf
Retomada
Tempo sugerido: 7 minutos (slides 3 e 4)
Orientações:
Inicialmente forme duplas com os alunos onde pelo menos um deles saiba preparar café. Peça para que um dos alunos leia o primeiro balão de fala da personagem e que o outro membro da dupla leia o segundo balão do outro personagem. Dê alguns minutos para que os alunos discutam como eles preparam o café e como elaborar um fluxograma mostrando as etapas do preparo. Peça para que os alunos fiquem atento ao tipo de símbolo utilizado de acordo com a ação executada e questione os mesmos sobre colocar ou não açúcar no café.
Depois que o fluxograma estiver pronto peça para que uma das duplas explique para os demais como elaboraram e a função de cada símbolo nele. O retângulo é destinado às ações a serem executadas, o losango para a tomada de decisões e o símbolo com cantos arredondados para o final do processo. Você pode utilizar o fluxograma do slide 4 para auxiliar na validação das produções dos alunos.
Propósito:
Familiarizar os alunos com os símbolos de um fluxograma e suas funções.
Discuta com a turma:
- Conte um para o outro como vocês preparam café em suas casas? Qual é a primeira coisa a ser feita? E depois?
- Todos costumam adoçar o café ou existe a possibilidade de adoçar depois? Como você indicaria isto em seu diagrama?
- Observando o diagrama do slide 4 tente descobrir a diferença entre as funções de cada símbolo.
Atividade principal

Tempo sugerido: 20 minutos (slides 5 a 7)
Orientações:
Entregue para cada dupla uma folha contendo os polígonos e seus ângulos externos. Peça para que eles calculem o valor dos ângulos externos em cada polígono e, depois, somem as medidas obtidas. Pergunte também se eles percebem algo em relação aos resultados encontrados. O objetivo desta etapa é levar o aluno a perceber que a soma dos ângulos externos de qualquer polígono sempre é 360º.
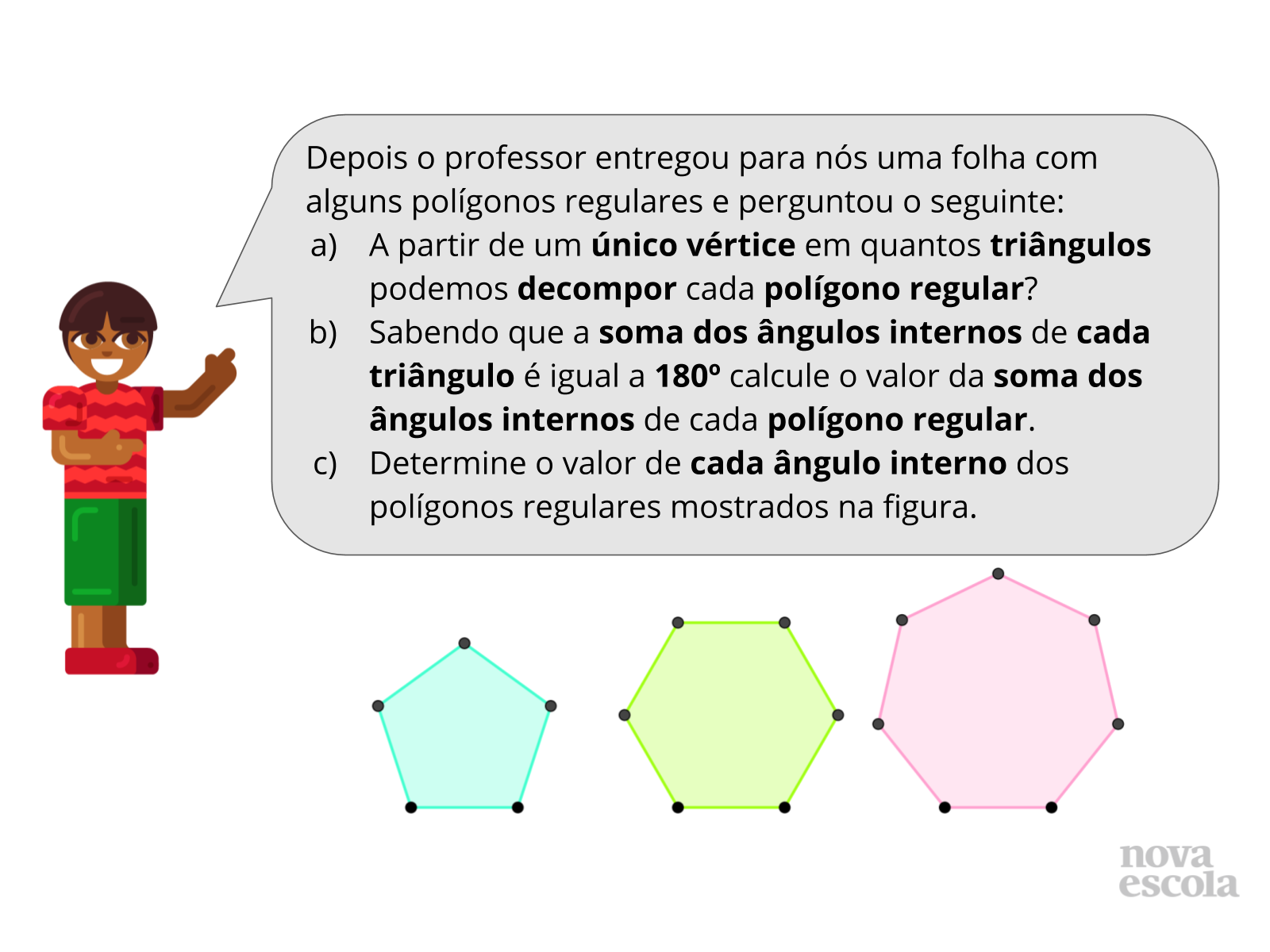
Em seguida projete ou desenhe os polígonos regulares do slide 6 e questione como os alunos poderiam determinar a medida do ângulo externo e de cada ângulo interno de cada polígono. A intenção neste momento é levar o aluno perceber que, como os ângulos internos de um polígono regular são congruentes, seus ângulos externos também serão (eles são suplementares). Logo para determinar o valor do ângulo externo basta dividir 360º pelo número de ângulos do polígono.
Por último peça para que os alunos elaborem um fluxograma mostrando como construir um polígono regular a partir da medida de seu ângulo externo. Neste caso é importante que os alunos escolham adequadamente os símbolos de acordo com o tipo de ação que será executada. Depois que os alunos terem elaborado o fluxograma solicite a eles que o utilize para construir um polígono regular com auxílio de régua e transferidor.
Propósito:
Elaborar um fluxograma para a construção de um polígono regular a partir da medida de um de seus ângulos externos.
Discuta com a turma:
- (Slide 5) Observando um único vértice do polígono o quê você percebe em relação ao ângulo externo e o ângulo interno? Como podemos determinar a medida do ângulo externo a partir da medida do ângulo interno? Depois que você somou os ângulos externos de todos polígonos, você notou algo? O quê?
- (Slide 6) O quê podemos afirmar sobre a medida dos ângulos internos de um polígono regular? E sobre a medidas dos ângulos externos? Como então determinar a medida de um ângulo externo de um polígono regular sabendo destas informações? E depois como podemos encontrar a medida do ângulo interno dele?
- (Slide 7) O quê devemos calcular primeiro para fazer a construção do polígono regular? E depois? Quando você encontrar o valor do ângulo interno o quê você deverá fazer para realizar a construção? E assim que você construiu o primeiro ângulo?
Materiais complementares:
Atividade principal para impressão: https://nova-escola-producao.s3.amazonaws.com/mdfhsFXPA2tjMx6XN5fqbTPWbkCtT3Uwf4NjgDUX3DUzHg58pvjQ5wKfJEaZ/atividade-principal-mat9-27geo05.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/CV3euEQE9WP6GPMeQGM3ggG3bQBtZc6tGQFxVwm2Qv6CZcdQ8w7E2n3WUqKE/resolucao-das-atividades-mat9-27geo05.pdf
Atividade principal
Tempo sugerido: 20 minutos (slides 5 a 7)
Orientações:
Entregue para cada dupla uma folha contendo os polígonos e seus ângulos externos. Peça para que eles calculem o valor dos ângulos externos em cada polígono e, depois, somem as medidas obtidas. Pergunte também se eles percebem algo em relação aos resultados encontrados. O objetivo desta etapa é levar o aluno a perceber que a soma dos ângulos externos de qualquer polígono sempre é 360º.
Em seguida projete ou desenhe os polígonos regulares do slide 6 e questione como os alunos poderiam determinar a medida do ângulo externo e de cada ângulo interno de cada polígono. A intenção neste momento é levar o aluno perceber que, como os ângulos internos de um polígono regular são congruentes, seus ângulos externos também serão (eles são suplementares). Logo para determinar o valor do ângulo externo basta dividir 360º pelo número de ângulos do polígono.
Por último peça para que os alunos elaborem um fluxograma mostrando como construir um polígono regular a partir da medida de seu ângulo externo. Neste caso é importante que os alunos escolham adequadamente os símbolos de acordo com o tipo de ação que será executada. Depois que os alunos terem elaborado o fluxograma solicite a eles que o utilize para construir um polígono regular com auxílio de régua e transferidor.
Propósito:
Elaborar um fluxograma para a construção de um polígono regular a partir da medida de um de seus ângulos externos.
Discuta com a turma:
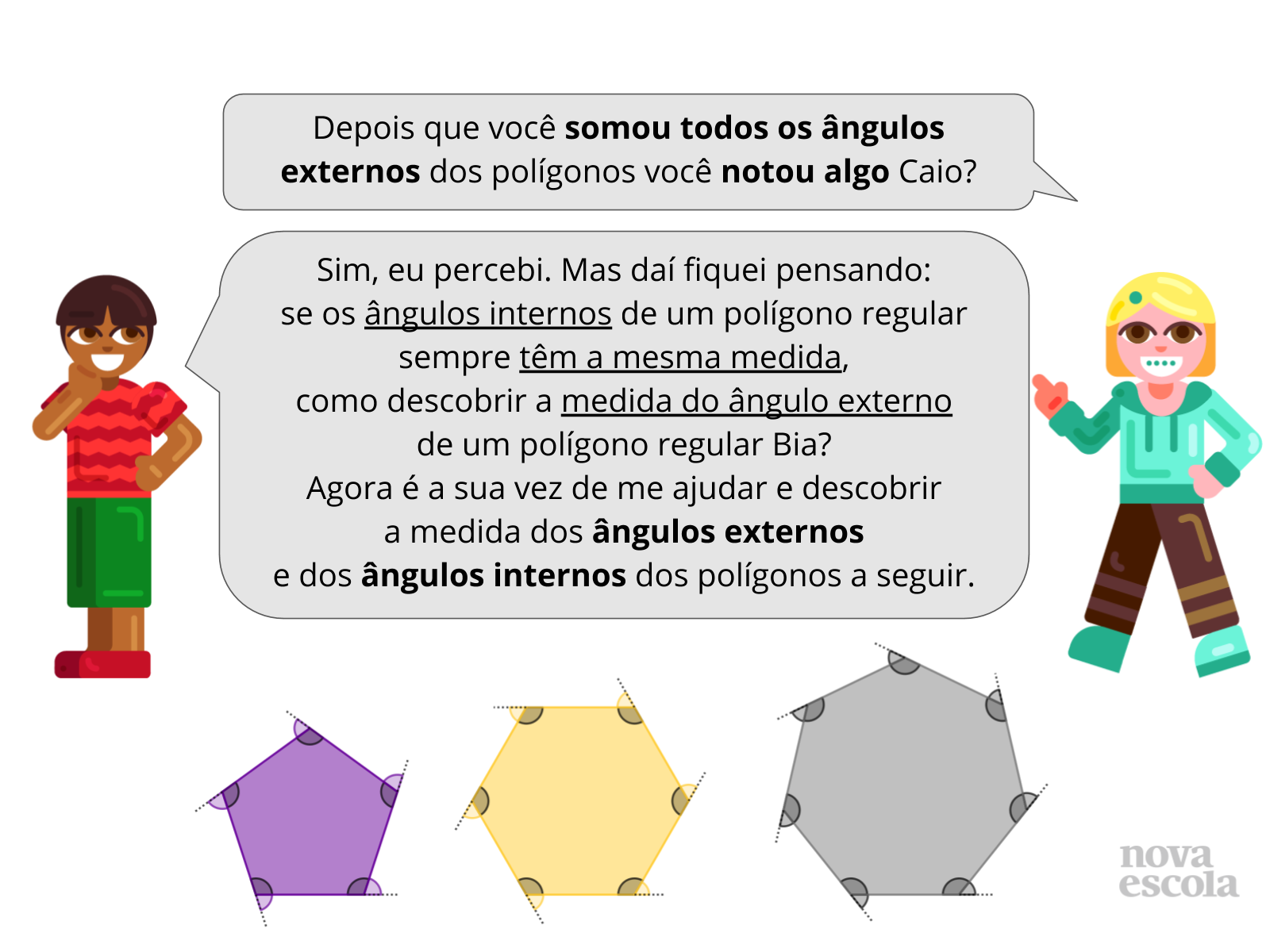
- (Slide 5) Observando um único vértice do polígono o quê você percebe em relação ao ângulo externo e o ângulo interno? Como podemos determinar a medida do ângulo externo a partir da medida do ângulo interno? Depois que você somou os ângulos externos de todos polígonos, você notou algo? O quê?
- (Slide 6) O quê podemos afirmar sobre a medida dos ângulos internos de um polígono regular? E sobre a medidas dos ângulos externos? Como então determinar a medida de um ângulo externo de um polígono regular sabendo destas informações? E depois como podemos encontrar a medida do ângulo interno dele?
- (Slide 7) O quê devemos calcular primeiro para fazer a construção do polígono regular? E depois? Quando você encontrar o valor do ângulo interno o quê você deverá fazer para realizar a construção? E assim que você construiu o primeiro ângulo?
Atividade principal
Tempo sugerido: 20 minutos (slides 5 a 7)
Orientações:
Entregue para cada dupla uma folha contendo os polígonos e seus ângulos externos. Peça para que eles calculem o valor dos ângulos externos em cada polígono e, depois, somem as medidas obtidas. Pergunte também se eles percebem algo em relação aos resultados encontrados. O objetivo desta etapa é levar o aluno a perceber que a soma dos ângulos externos de qualquer polígono sempre é 360º.
Em seguida projete ou desenhe os polígonos regulares do slide 6 e questione como os alunos poderiam determinar a medida do ângulo externo e de cada ângulo interno de cada polígono. A intenção neste momento é levar o aluno perceber que, como os ângulos internos de um polígono regular são congruentes, seus ângulos externos também serão (eles são suplementares). Logo para determinar o valor do ângulo externo basta dividir 360º pelo número de ângulos do polígono.
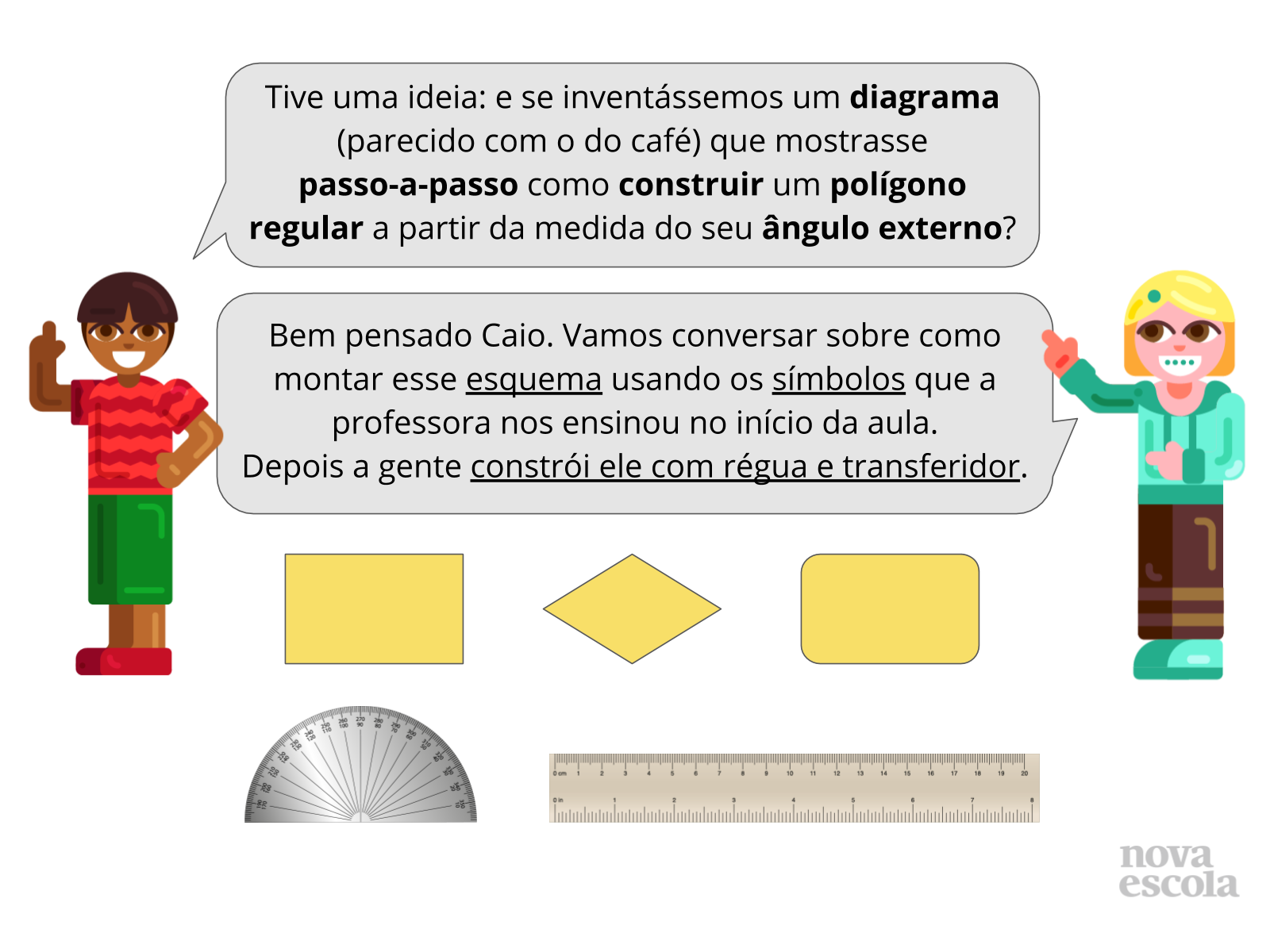
Por último peça para que os alunos elaborem um fluxograma mostrando como construir um polígono regular a partir da medida de seu ângulo externo. Neste caso é importante que os alunos escolham adequadamente os símbolos de acordo com o tipo de ação que será executada. Depois que os alunos terem elaborado o fluxograma solicite a eles que o utilize para construir um polígono regular com auxílio de régua e transferidor.
Propósito:
Elaborar um fluxograma para a construção de um polígono regular a partir da medida de um de seus ângulos externos.
Discuta com a turma:
- (Slide 5) Observando um único vértice do polígono o quê você percebe em relação ao ângulo externo e o ângulo interno? Como podemos determinar a medida do ângulo externo a partir da medida do ângulo interno? Depois que você somou os ângulos externos de todos polígonos, você notou algo? O quê?
- (Slide 6) O quê podemos afirmar sobre a medida dos ângulos internos de um polígono regular? E sobre a medidas dos ângulos externos? Como então determinar a medida de um ângulo externo de um polígono regular sabendo destas informações? E depois como podemos encontrar a medida do ângulo interno dele?
- (Slide 7) O quê devemos calcular primeiro para fazer a construção do polígono regular? E depois? Quando você encontrar o valor do ângulo interno o quê você deverá fazer para realizar a construção? E assim que você construiu o primeiro ângulo?
Discussão das soluções
Tempo sugerido: 10 minutos (slides 8 a 10)
Orientações:
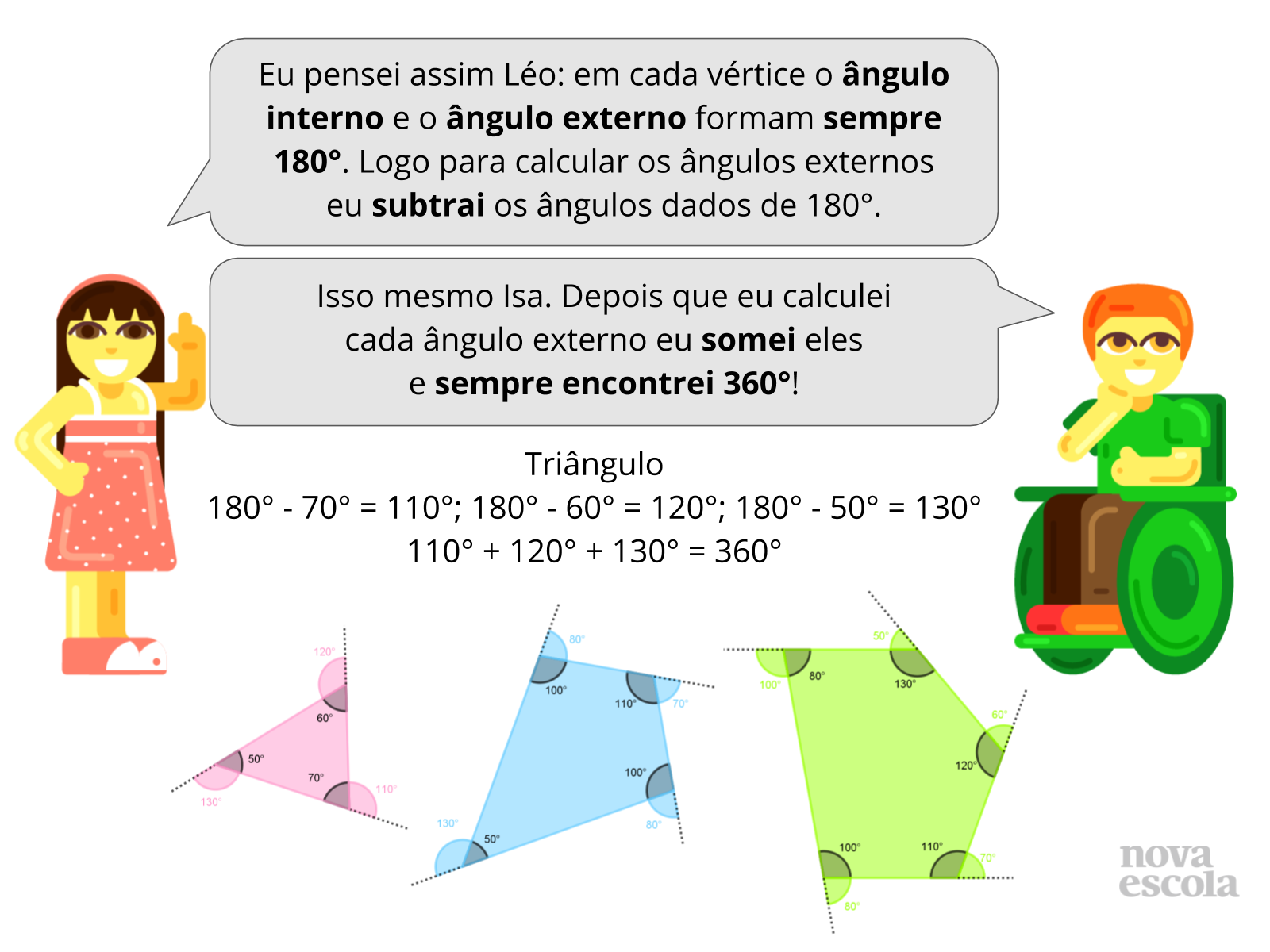
Escolha algumas produções (certas e erradas) elaboradas pelos alunos para fazer a discussão junto a turma. Inicie perguntando como os alunos determinaram o valor dos ângulos externos dos polígonos. Continue questionando os alunos sobre o quê perceberam em relação à soma das medidas dos ângulos externos dos polígonos (sempre resulta em 360°).
Assim que todos alunos compreenderem este resultado peça para que os alunos expliquem como eles determinaram o valor de cada ângulo externo e, também, de cada ângulo interno (basta dividir 360° pelo número de ângulos do polígono).
Por último solicite que os alunos expliquem como elaboraram o fluxograma para a construção do polígono regular. Pergunte sobre as etapas necessárias para a construção do polígono, os símbolos utilizados no fluxograma e que se alguém repetir o procedimento mostrado no fluxograma obterá resultado semelhante.
Propósito:
Discutir as produções dos alunos em relação à elaboração de um fluxograma para construção do polígono regular a partir da medida de seu ângulo externo.
Discuta com a turma:
- Como vocês fizeram para encontrar a medida dos ângulos externos dos polígonos? Depois que somaram as medidas dos ângulos externos vocês notaram algo? O quê?
- O quê vocês sabem sobre as medidas dos ângulos internos de um polígono regular? E sobre os ângulos externos? Como vocês pensaram para descobrir a medida desses ângulos?
- No momento que foram elaborar o fluxograma quais foram as ações necessárias para construir o polígono? Todos os símbolos utilizados são iguais? Explique a função de cada símbolo de seu fluxograma.
Materiais complementares:
Guia de intervenção: https://nova-escola-producao.s3.amazonaws.com/vNwzb5tAzbxM78N8sQekaUbSSyy9CTQupsU5JejRuE494uCzePBaR7TNJS6j/guia-de-intervencoes-mat9-27geo05.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/CV3euEQE9WP6GPMeQGM3ggG3bQBtZc6tGQFxVwm2Qv6CZcdQ8w7E2n3WUqKE/resolucao-das-atividades-mat9-27geo05.pdf
Discussão das soluções
Tempo sugerido: 10 minutos (slides 8 a 10)
Orientações:
Escolha algumas produções (certas e erradas) elaboradas pelos alunos para fazer a discussão junto a turma. Inicie perguntando como os alunos determinaram o valor dos ângulos externos dos polígonos. Continue questionando os alunos sobre o quê perceberam em relação à soma das medidas dos ângulos externos dos polígonos (sempre resulta em 360°).
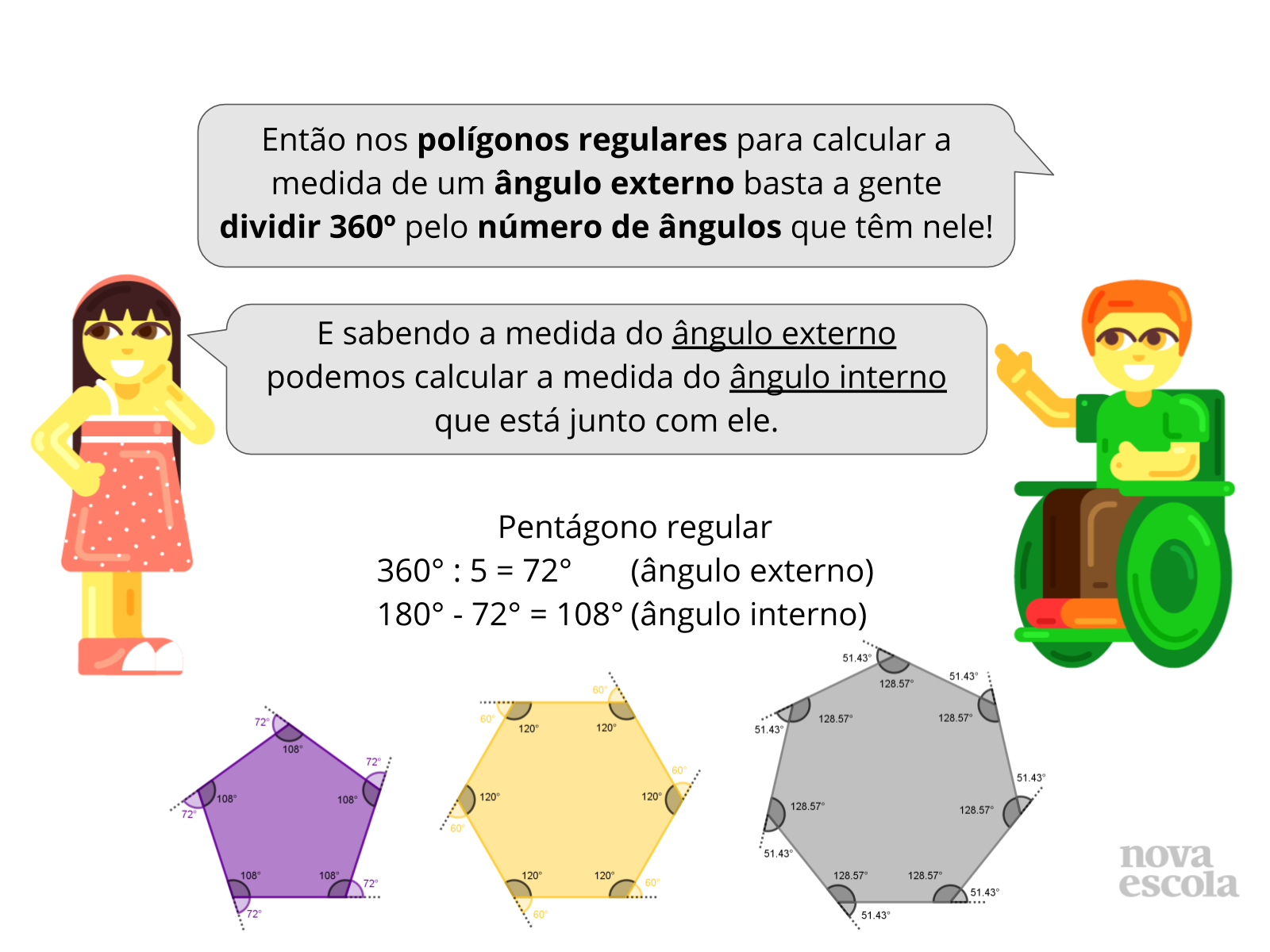
Assim que todos alunos compreenderem este resultado peça para que os alunos expliquem como eles determinaram o valor de cada ângulo externo e, também, de cada ângulo interno (basta dividir 360° pelo número de ângulos do polígono).
Por último solicite que os alunos expliquem como elaboraram o fluxograma para a construção do polígono regular. Pergunte sobre as etapas necessárias para a construção do polígono, os símbolos utilizados no fluxograma e que se alguém repetir o procedimento mostrado no fluxograma obterá resultado semelhante.
Propósito:
Discutir as produções dos alunos em relação à elaboração de um fluxograma para construção do polígono regular a partir da medida de seu ângulo externo.
Discuta com a turma:
- Como vocês fizeram para encontrar a medida dos ângulos externos dos polígonos? Depois que somaram as medidas dos ângulos externos vocês notaram algo? O quê?
- O quê vocês sabem sobre as medidas dos ângulos internos de um polígono regular? E sobre os ângulos externos? Como vocês pensaram para descobrir a medida desses ângulos?
- No momento que foram elaborar o fluxograma quais foram as ações necessárias para construir o polígono? Todos os símbolos utilizados são iguais? Explique a função de cada símbolo de seu fluxograma.
Discussão das soluções
Tempo sugerido: 10 minutos (slides 8 a 10)
Orientações:
Escolha algumas produções (certas e erradas) elaboradas pelos alunos para fazer a discussão junto a turma. Inicie perguntando como os alunos determinaram o valor dos ângulos externos dos polígonos. Continue questionando os alunos sobre o quê perceberam em relação à soma das medidas dos ângulos externos dos polígonos (sempre resulta em 360°).
Assim que todos alunos compreenderem este resultado peça para que os alunos expliquem como eles determinaram o valor de cada ângulo externo e, também, de cada ângulo interno (basta dividir 360° pelo número de ângulos do polígono).
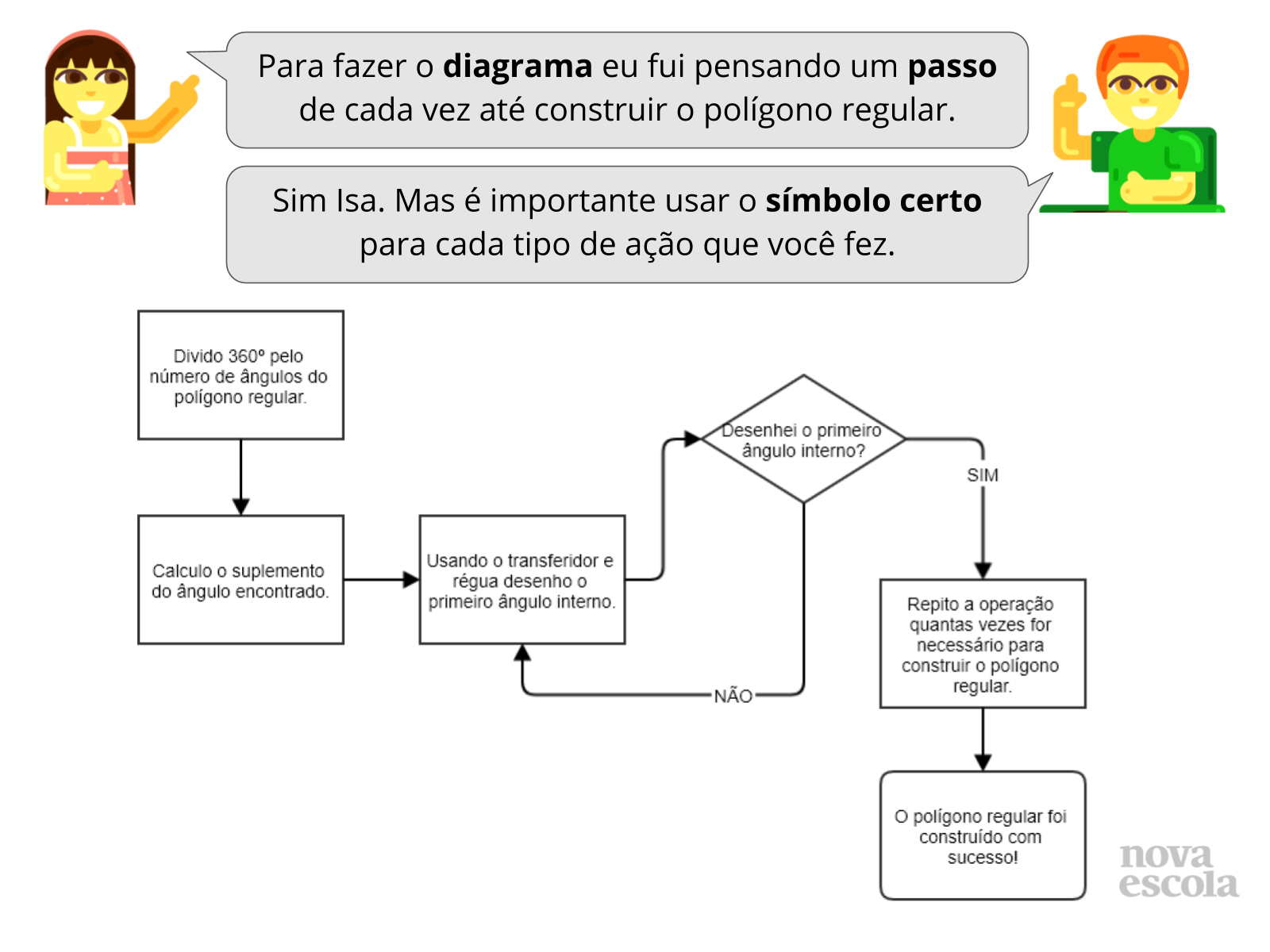
Por último solicite que os alunos expliquem como elaboraram o fluxograma para a construção do polígono regular. Pergunte sobre as etapas necessárias para a construção do polígono, os símbolos utilizados no fluxograma e que se alguém repetir o procedimento mostrado no fluxograma obterá resultado semelhante.
Propósito:
Discutir as produções dos alunos em relação à elaboração de um fluxograma para construção do polígono regular a partir da medida de seu ângulo externo.
Discuta com a turma:
- Como vocês fizeram para encontrar a medida dos ângulos externos dos polígonos? Depois que somaram as medidas dos ângulos externos vocês notaram algo? O quê?
- O quê vocês sabem sobre as medidas dos ângulos internos de um polígono regular? E sobre os ângulos externos? Como vocês pensaram para descobrir a medida desses ângulos?
- No momento que foram elaborar o fluxograma quais foram as ações necessárias para construir o polígono? Todos os símbolos utilizados são iguais? Explique a função de cada símbolo de seu fluxograma.
Encerramento
Tempo sugerido: 3 minutos
Orientações:
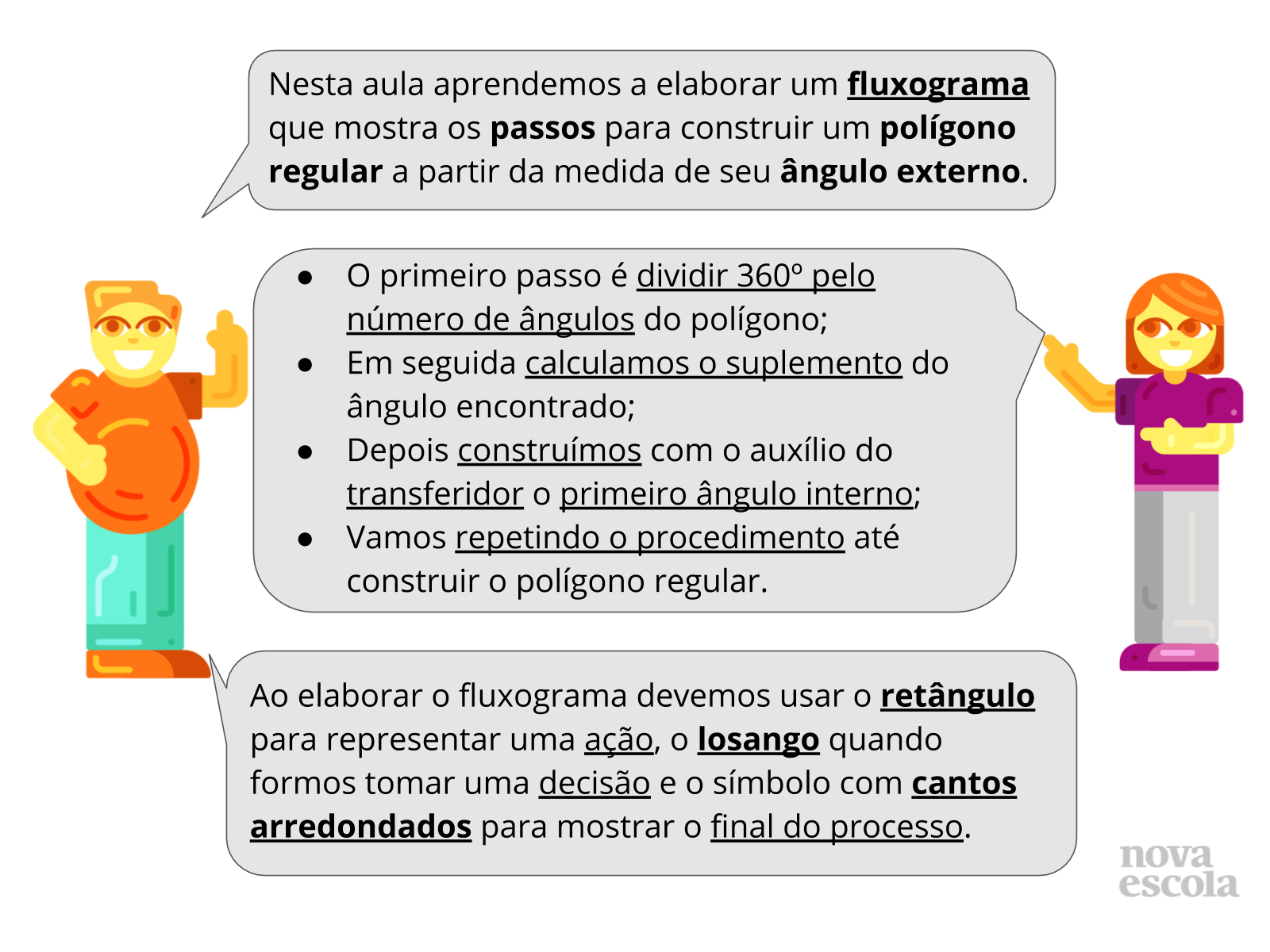
Leia as instruções contidas nos balões de fala para formalizar as etapas desenvolvidas pelos alunos ao longo da aula. Durante a leitura enfatize que o fluxograma é uma maneira de organizar as etapas de um processo que, neste caso, foi a construção do polígono regular. Comente também que este tipo de diagrama pode ser aplicado em diversas situações. Caso sinta necessidade peça para que os alunos anotarem as etapas utilizadas na construção do polígono regular.
Propósito:
Auxiliar o aluno na formalização do conceito de fluxograma e mostrar uma possível aplicação na Geometria (construção do polígono regular).
Discuta com a turma:
- Quais foram as etapas que desenvolvemos ao longo desta aula?
- O quê você julga importante na elaboração de um fluxograma?
- Onde podemos utilizar fluxogramas em nosso cotidiano?
Raio X
Tempo sugerido: 8 minutos
Orientações:
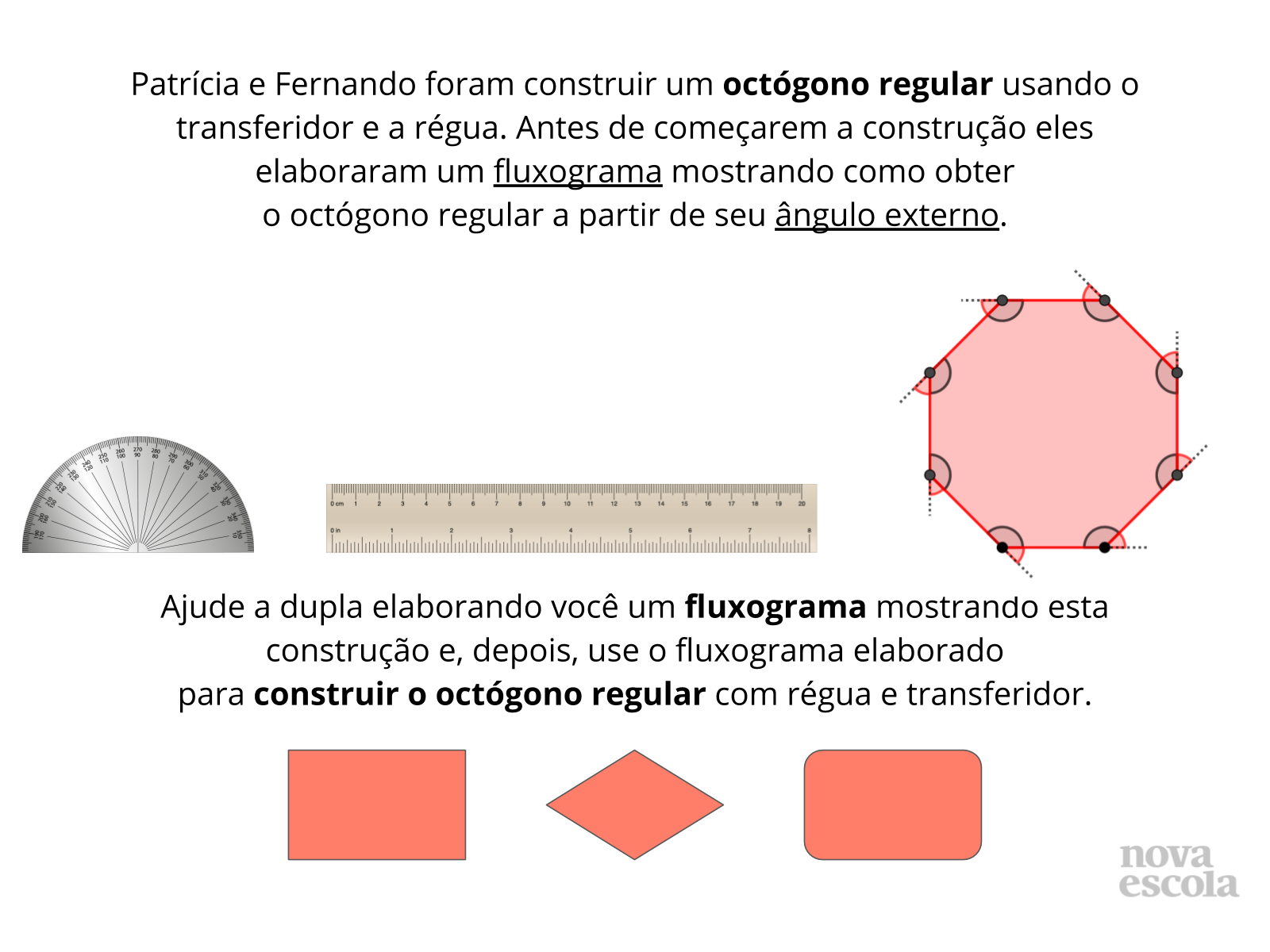
Leia o comando da atividade e peça para que cada aluno, individualmente, elabore um fluxograma para a construção de um octógono regular. Em seguida, como auxílio de régua e transferidor, solicite que o aluno faça a construção do octógono regular utilizando o fluxograma que elaborou anteriormente. Por último recolha as atividade para analisar se os alunos desenvolveram adequadamente o objetivo previsto no início da aula.
Propósito:
Verificar se o aluno consegue elaborar um fluxograma para a construção de um octógono regular a partir da medida de seu ângulo externo.
Discuta com a turma:
- Qual é a primeira informação que você deve determinar para construir o octógono regular? E a segunda informação?
- Quais símbolos você deve utilizar para elaborar o fluxograma? Em qual ordem devemos colocar as ações para obter o octógono regular?
- Se outra pessoa utilizar seu fluxograma ela obterá no final o octógono regular?
Materiais complementares:
Atividade para impressão: https://nova-escola-producao.s3.amazonaws.com/NTnNYCRFAKyFtEY7BEsEW3cMB3CrT5J3YjwkqRwNWfPctR564c56B3vvrSvt/atividade-raio-x-mat9-27geo05.pdf
Atividades complementares: https://nova-escola-producao.s3.amazonaws.com/gREHaMdY7ngJHcEqKDaxrdX8Bq82EQ4NkQGcqAC6v6jNpGt4ZkjeAN7dHBPW/atividade-complementar-mat9-27geo05.pdf
Resolução das atividades: https://nova-escola-producao.s3.amazonaws.com/CV3euEQE9WP6GPMeQGM3ggG3bQBtZc6tGQFxVwm2Qv6CZcdQ8w7E2n3WUqKE/resolucao-das-atividades-mat9-27geo05.pdf
Para o professor
Para o aluno
Sugestão de adaptação para ensino remoto
Código do plano
MAT9_27GEO05
Recursos
- Necessários:, WhatsApp, Papel, Lápis, Papel, Régua.
- Opcionais: Meet, Hangout, Zoom, Mobizen ou Loon..
Para este plano, foque na etapa Atividade Principal
Aquecimento
Fotografe o fluxograma do slide 3 e compartilhe no grupo de WhatsApp juntamente com o enunciado da atividade. Solicite que os alunos compartilhem o significado de cada figura utilizada num fluxograma.
Atividade principal
Apresente no grupo de WhatsApp cada uma das 4 etapas da Atividade Principal, disponível nos materiais impressos, separadamente. Utilize as questões propostas no Discuta com a turma para que os alunos registrem suas respostas no caderno. Para cada etapa solicite a alguns alunos que compartilhem suas respostas do grupo de WhatsApp, desse modo você pode garantir a participação da turma toda. Você pode utilizar o arquivo de Apresentações dessa aula com os aplicativos Mobizen ou Loon para gravar as explicações e encaminhar via WhatsApp para os alunos. Caso seus alunos não tenham acesso à Internet disponibilize esta adaptação impressa a partir dos documentos de impressão deste plano de aula e oriente-os a fazer um Diário com suas resoluções das atividades propostas e registros de como escolheu a estratégia de resolução.
Discussão das soluções
A partir das respostas apresentadas pelos alunos via WhatsApp faça as intervenções necessárias de modo que fique claro o procedimento para o cálculo da medida do ângulo externo. Compartilhe com os alunos o slide 9 também para que tenham como comparar o fluxograma que fizeram.
Sistematização
xxxxxx
Encerramento
xxxxx
Raio X
O Raio X pode ser usado como forma de revisão das aprendizagens, assim como também as atividades complementares, ou ainda como processo de verificação de aprendizagem.
Convite às famílias
Nem sempre a família pode participar desse momento por não serem professores de matemática, mas é possível que auxiliem na discussão de possibilidades de resolução dos problemas propostos.
Sobre o plano - MAT9_27GEO05 / Programando um polígono regular?!
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Fabricio Eduardo Ferreira.
Mentor: Rodrigo Morozetti Blanco
Habilidade da BNCC
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
Objetivos específicos
- Familiarizar o aluno com a simbologia utilizada na elaboração de um fluxograma;
- Calcular o valor de um ângulo externo a partir da medida de seu suplemento (ângulo interno);
- Determinar o valor da medida de um ângulo externo a partir da soma dos ângulos externos de um polígono regular;
- Descrever por meio de um fluxograma os passos para a obtenção de um polígono regular.