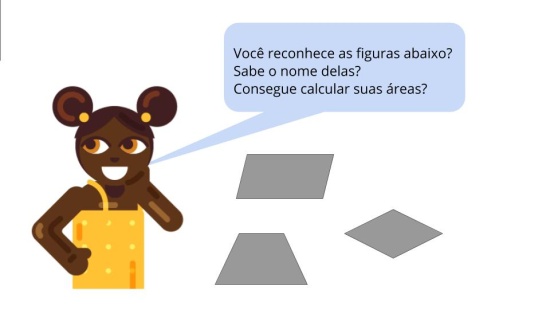
Guia de Intervenção
Plano de Aula
Plano de aula: As malhas no cálculo de áreas
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Medição de superfícies
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alex de Cassio Macedo
Mentora: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF07MA26) Resolver e elaborar problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas.
Objetivos específicos
Analisar a importância das decomposições de figuras planas no cálculo de medidas de superfície (área).
Conceito-chave
Composição e decomposição de figuras planas.
Recursos necessários
- Atividades impressas em folhas.
- Régua, lápis, borracha, caderno.
- Tesoura, cola (opcional).
Habilidades BNCC:
Objetivos de aprendizagem
Analisar a importância das decomposições de figuras planas no cálculo de medidas de superfície (área).
Resumo da aula
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo da aula

Tempo sugerido: 2 minutos.
Orientação: Neste primeiro momento explique o objetivo da aula de maneira clara e sucinta, argumente que a partir desta aula o aluno(a) será capaz de calcular medidas de superfície ou áreas em diversas situações, decompondo-as em figuras mais simples e conhecidas.
Propósito: Compartilhar o objetivo da aula e motivá-los ao estudo.
Discuta com a turma:
- É claro o sentido da palavra decomposição?
- Segundo o dicionário : Decompor é separação dos elementos formadores ou constituintes de algo.
- Peça que eles exemplifiquem uma figura cuja a expressão de área é desconhecida por eles.
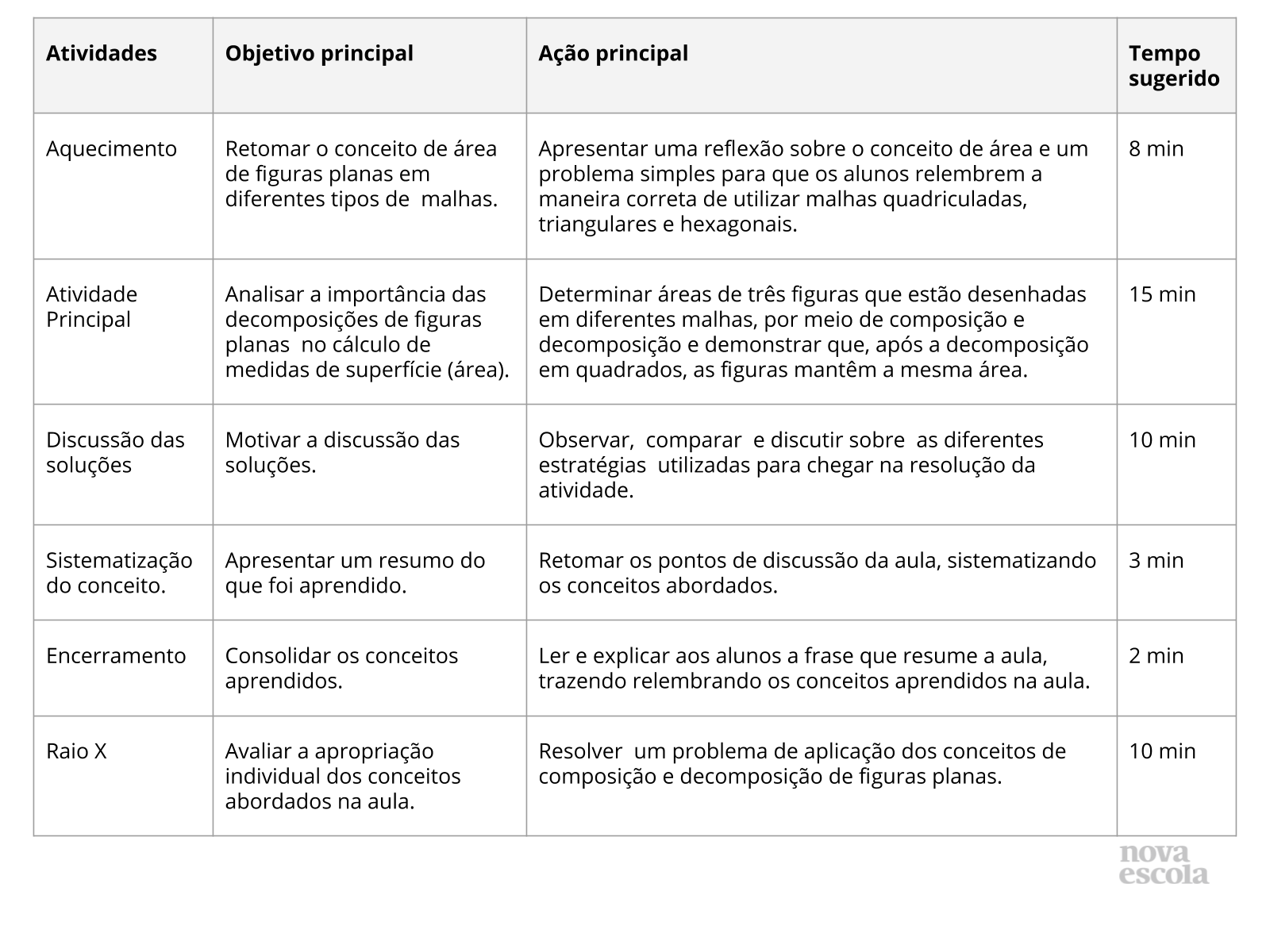
Aquecimento

Tempo previsto: 10 minutos (slide 3 ao slide 9).
Orientações: Neste momento é importante retomar os conceitos de área, a utilização de malhas; quadriculadas , triangulares e hexagonais, na determinação de áreas de figuras planas, cuide para não revelar a resolução préviamente do problema proposto.
Propósito: Promover uma retomada de conceitos relacionados ao cálculo de áreas.
Discuta com a turma:
- Quem lembra o que significa a medida de área?
- Deixe que os alunos expressem seus conhecimentos livremente.Peça-lhes exemplos.
- Porque é util sabermos calcular áreas?
Professor, para melhor orientar seus alunos sobre Medidas de superfície: como escrever e converter as unidades de medida relativas a áreas clique aqui.
- Podemos citar diversas aplicações, na construção, na arte, na geografia. Deixe que eles levantem algumas aplicações.
Professor, comente com seus alunos que o metro quadrado (m²) é a medida mais utilizada na medição de áreas, mas em algumas ocasiões, outras unidades de medidas como o km² são utilizadas. Por exemplo, na previsão da área de uma reserva florestal ou na medição de um lago de uma usina hidrelétrica, o km² é considerado uma medida mais usual, pois expressa superfícies de grandes extensões. Para melhor orientar seus alunos clique aqui.
Aquecimento

Tempo previsto: 10 minutos (slide 3 ao slide 9).
Orientações: Chame a atenção para as formas que cada malha é criada.
Propósito: Promover uma retomada de conceitos relacionados ao uso de malhas para a determinação de áreas.
Discuta com a turma:
- Quem já utilizou malha quadriculada? Para relembrar o cálculo com números decimais e fracionários, da área de figuras planas, em uma malha quadriculada clique aqui.
- Verifique o nível de conhecimento da turma neste momento, dependendo do que eles responderem o aquecimento deve ser mais detalhado para que a atividade possa funcionar bem com a turma.
Aquecimento

Tempo previsto: 10 minutos (slide 3 ao slide 9).
Orientações: Deixe que os alunos respondam livremente.
Propósito: Promover uma retomada de conceitos relacionados ao uso de malhas para a determinação de áreas.
Aquecimento

Tempo previsto: 10 minutos (slide 3 ao slide 9).
Orientações: Professor, reproduza o desenho na lousa ou projete o slide e mostre (apontando) os quadrados enquanto conta, isso ajudará os alunos a perceberem a facilidade em determinar a medida de área solicitada.
Propósito: Promover uma retomada de conceitos relacionados ao uso de malhas para a determinação de áreas.
Aquecimento
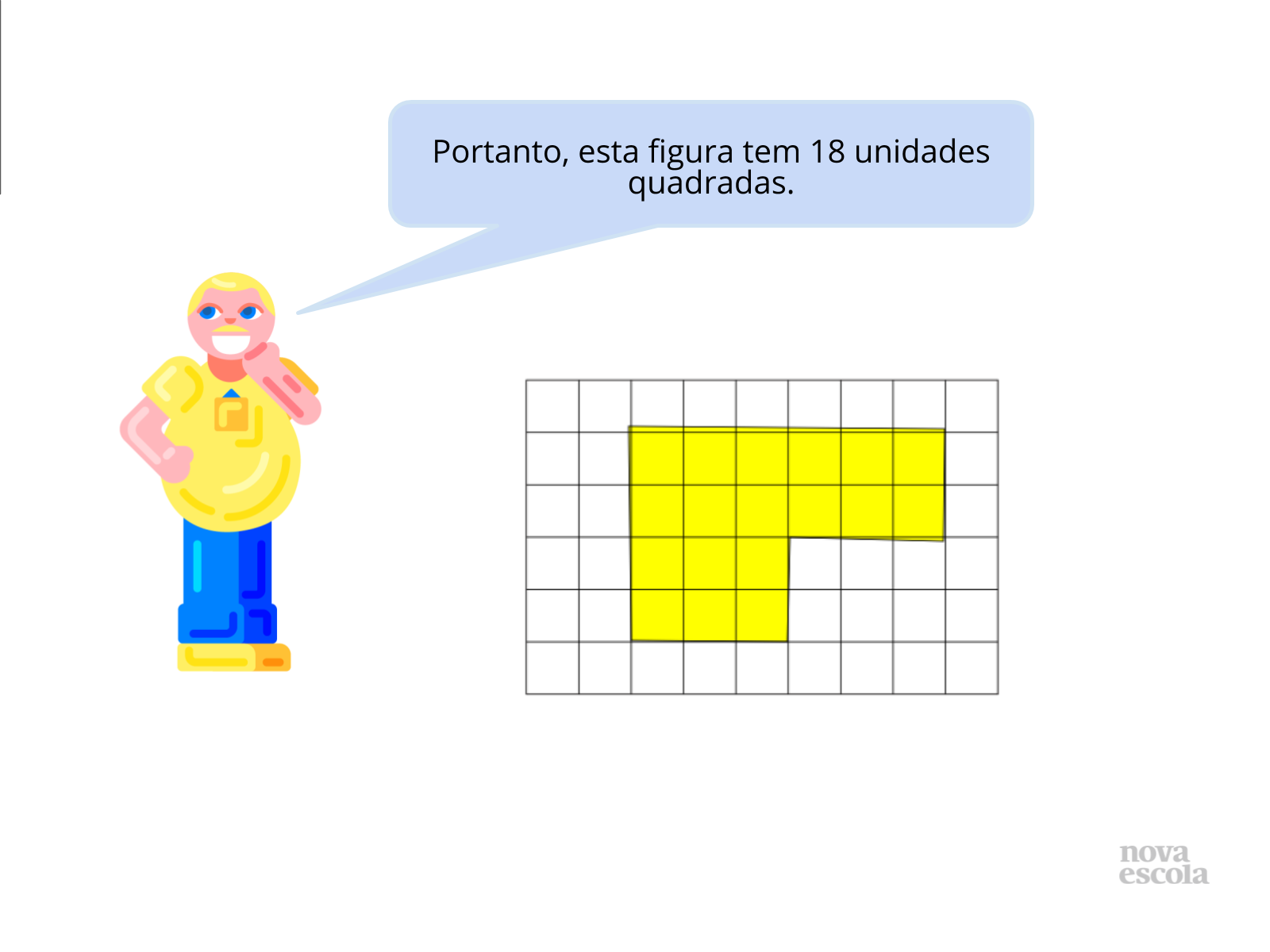
Tempo previsto: 10 minutos (slide 3 ao slide 9).
Orientações: Professor, reproduza o desenho na lousa ou projete o slide e mostre (apontando) os quadrados enquanto conta, isso ajudará os alunos a perceberem a facilidade em determinar a medida de área solicitada.
Propósito: Promover uma retomada de conceitos relacionados ao uso de malhas para a determinação de áreas.
Discuta com a turma:
- Tem alguma outra maneira de contar a quantidade quadrados coloridos da figura?
- Os alunos podem lembrar do processo de multiplicação e aprimorar a contagem dessa figura, por exemplo, percebendo que existem dois retângulos um de 2 x 6 e outro de 2 x 3, o que resultaria em 18 quadrados (12 + 6)
Aquecimento
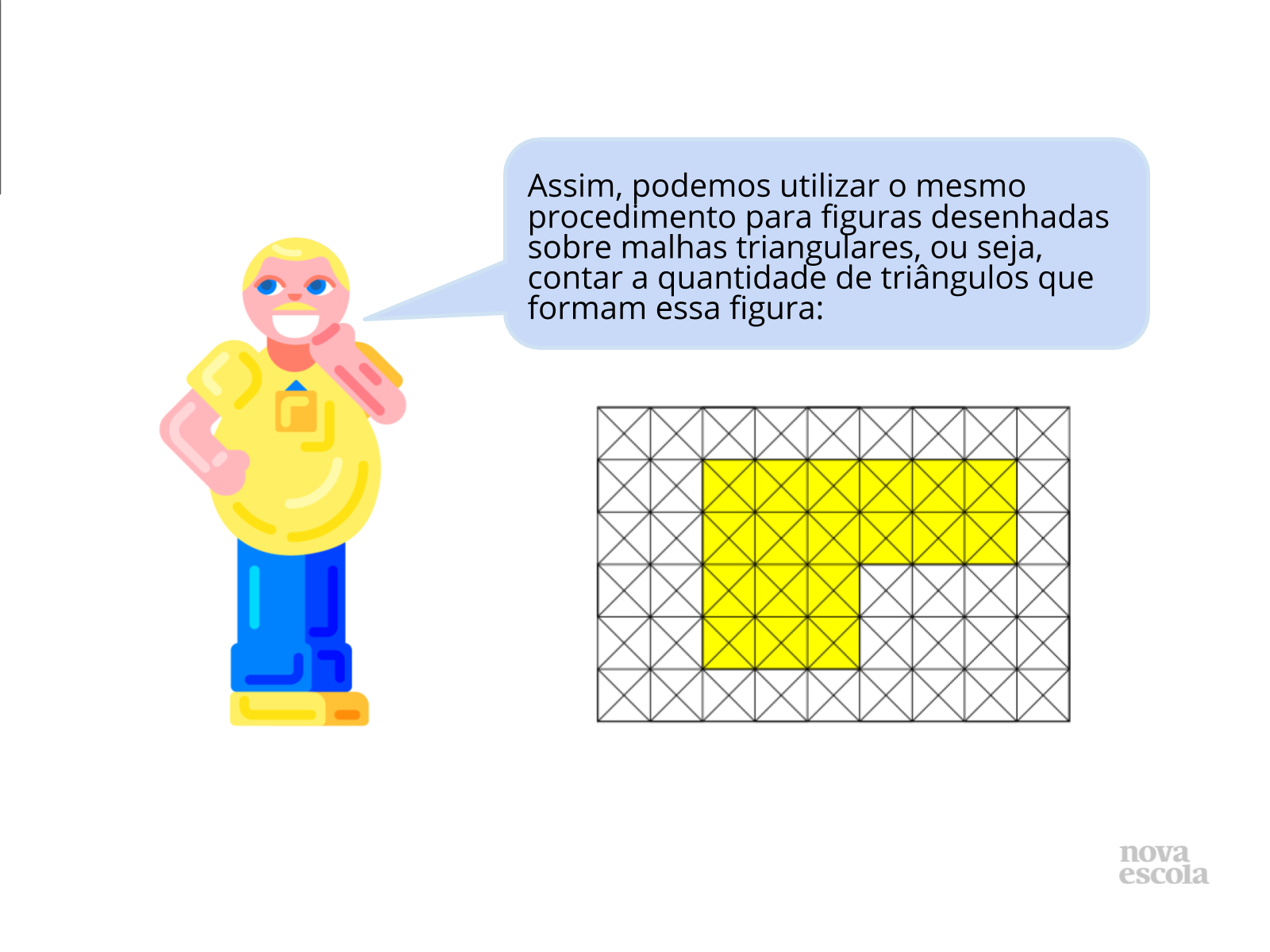
Tempo previsto: 10 minutos (slide 3 ao slide 9).
Orientações: Mostre os detalhes da malha, seu padrão, evidencie que, assim como os quadrados, os triângulos também preenchem toda a figura.
Propósito: Promover uma retomada de conceitos relacionados ao uso de malhas para a determinação de áreas.
Discuta com a turma:
- Quantos triângulo possuem esta figura, aproximadamente sem contar?
- É possível que algum aluno perceba que nesta malha cada quadrado (da malha anterior) está subdividido em quatro triângulos, e que portanto, cada triângulo é um quarto do quadrado da outra malha. Como a figura amarela é a mesma, o resultado numérico será o quádruplo do anterior.
Aquecimento
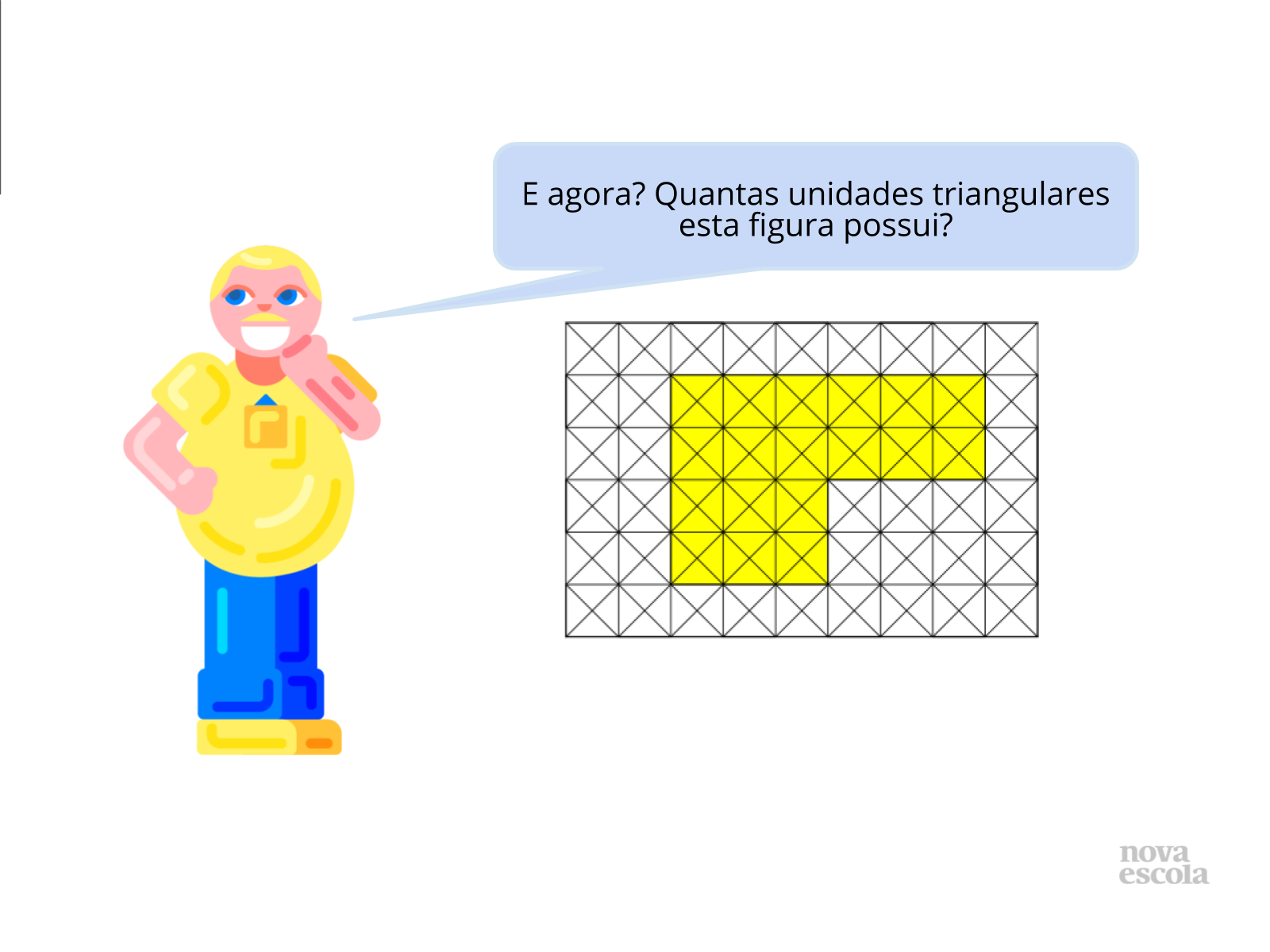
Tempo previsto: 10 minutos (slide 3 ao slide 9).
Orientações: Vá até a lousa ou a projeção e mostre (apontando) os triângulos enquanto conta, isso ajudará os alunos a perceberem a facilidade em determinar a quantidade solicitada.
Propósito: Promover uma retomada de conceitos relacionados ao uso de malhas para a determinação de áreas.
Resultado: 72 unidades triangulares.
Atividade Principal (parte I)

Tempo previsto: 8 minutos (slide 10 ao slide 13).
Orientações: Deixe que os alunos trabalhem em duplas e discutam suas soluções, visite as duplas e provoque com questionamentos sobre o encaminhamento das soluções sem, contudo interferir na estratégia de solução.
Propósito: Ler, interpretar e esclarecer os detalhes do problema.
Discuta com as duplas:
- O que é necessário saber para resolver o problema?
- Determinar uma maneira de obter quantidades inteiras de unidades de área na malha.
- Como é possível contar com segurança quantas unidades cabem em cada figura?
- Será que imaginando cortes na figura a solução não é mais fácil?
- O que mudou da malha quadrada para a triangular e a hexagonal?
- Teria outra maneira de encontrar este resultado? Mais simples por exemplo?
- Só tem esta maneira de representar esta solução?
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Atividade Principal (parte I)

Tempo previsto: 8 minutos (slide 10 ao slide 13).
Orientações: Deixe que os alunos trabalhem em duplas e discutam suas soluções, visite as duplas e provoque com questionamentos sobre o encaminhamento das soluções sem, contudo interferir na estratégia de solução.
Propósito: Ler, interpretar e esclarecer os detalhes do problema.
Discuta com as duplas:
- O que é necessário saber para resolver o problema?
- Determinar uma maneira de obter quantidades inteiras de unidades de área na malha.
- Como é possível contar com segurança quantas unidades cabem em cada figura?
- Será que imaginando cortes na figura a solução não é mais fácil?
- O que mudou da malha quadrada para a triangular e a hexagonal?
- Teria outra maneira de encontrar este resultado? Mais simples por exemplo?
- Só tem esta maneira de representar esta solução?
Atividade Principal (parte I)
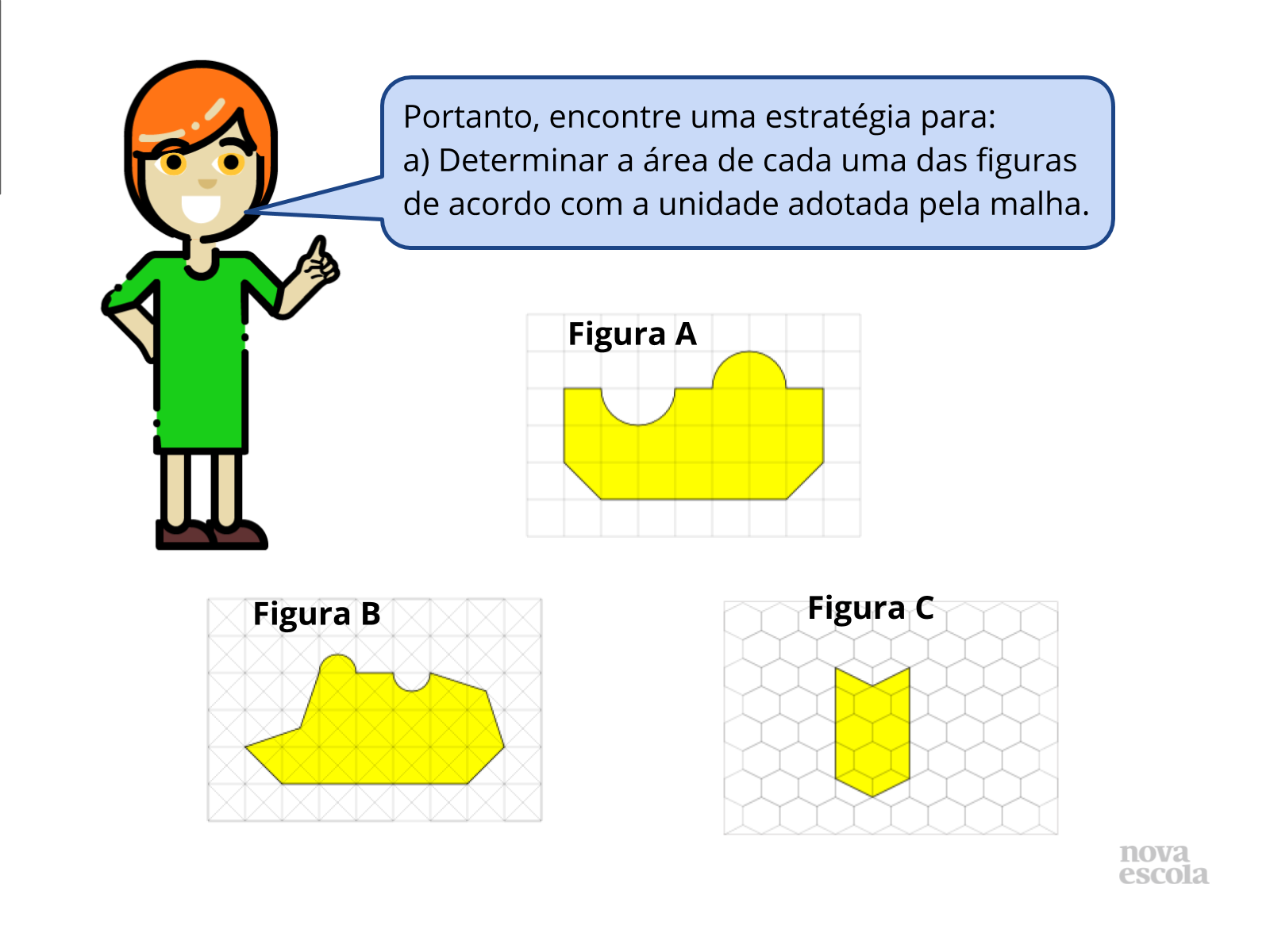
Tempo previsto: 8 minutos (slide 10 ao slide 13).
Orientações: Deixe que os alunos trabalhem em duplas e discutam suas soluções, visite as duplas e provoque com questionamentos sobre o encaminhamento das soluções sem, contudo interferir na estratégia de solução.
Propósito: Ler, interpretar e esclarecer os detalhes do problema.
Discuta com as duplas:
- O que é necessário saber para resolver o problema?
- Determinar uma maneira de obter quantidades inteiras de unidades de área na malha.
- Como é possível contar com segurança quantas unidades cabem em cada figura?
- Será que imaginando cortes na figura a solução não é mais fácil?
- O que mudou da malha quadrada para a triangular e a hexagonal?
- Teria outra maneira de encontrar este resultado? Mais simples por exemplo?
- Só tem esta maneira de representar esta solução?
Discussão das soluções ( parte I)
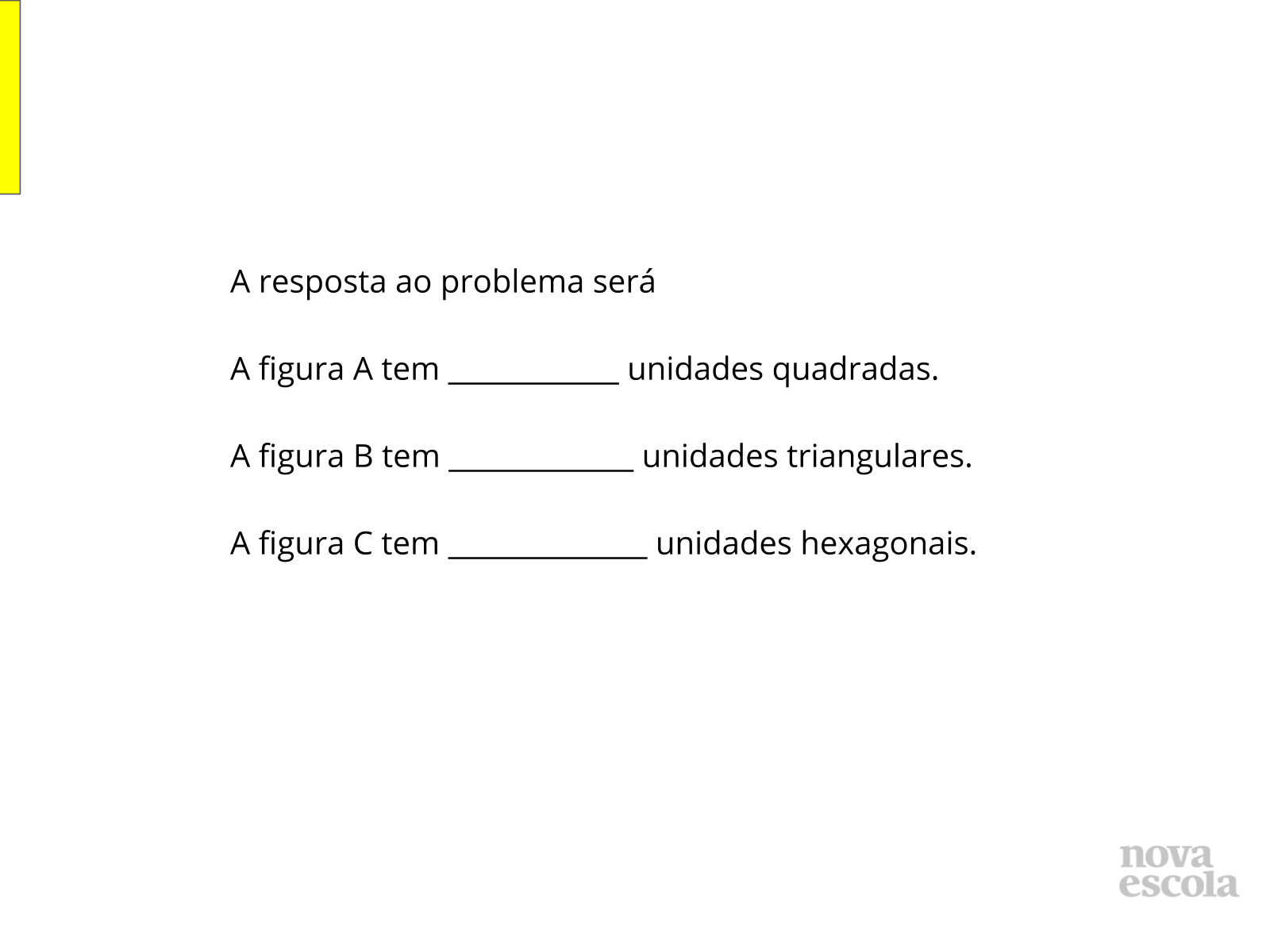
Tempo previsto: 8 minutos (slide 10 ao slide 13).
Orientações: Deixe que os alunos trabalhem em duplas e discutam suas soluções, visite as duplas e provoque com questionamentos o encaminhamento das soluções sem contudo interferir na estratégia de solução.
Propósito: Ler, interpretar e esclarecer os detalhes do problema.
Discuta com as duplas:
- O que é necessário saber para resolver o problema?
- Determinar uma maneira de obter quantidades inteiras de unidades de área na malha.
- Como é possível contar com segurança quantas unidades cabem em cada figura?
- Será que imaginando cortes na figura a solução não é mais fácil?
- O que mudou da malha quadrada para a triangular e a hexagonal?
- Teria outra maneira de encontrar este resultado? Mais simples por exemplo?
- Só tem esta maneira de representar esta solução?
Atividade Principal (parte II)
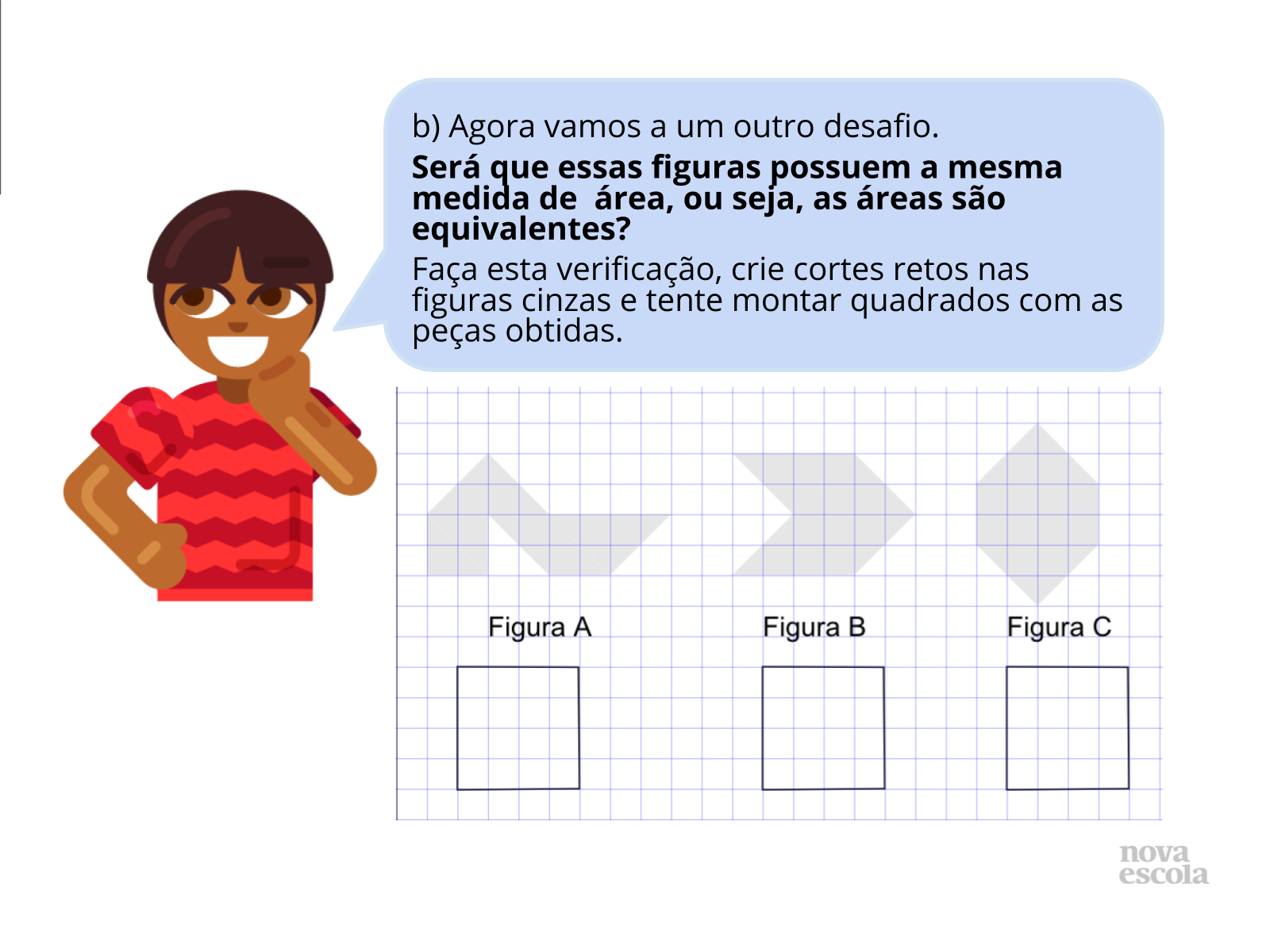
Tempo previsto: 7 minutos .
Orientações: Antes do início da atividade provoque seus alunos:
- Será que estas figuras têm a mesma área?
Em seguida, deixe que os alunos trabalhem em duplas e discutam suas soluções, visite as duplas e provoque com questionamentos o encaminhamento das soluções sem, contudo, interferir na estratégia de solução. Caso os alunos demonstram muita dificuldade sugira a eles reproduzirem as figuras em um papel (à parte) e recorte -os, pode ser mais simples para alguns alunos.
Propósito: Ler, interpretar e esclarecer os detalhes do problema.
Discuta com as duplas:
- Será que este problema só tem uma solução? Tente encontrar outro!
Discussão das soluções (parte I)
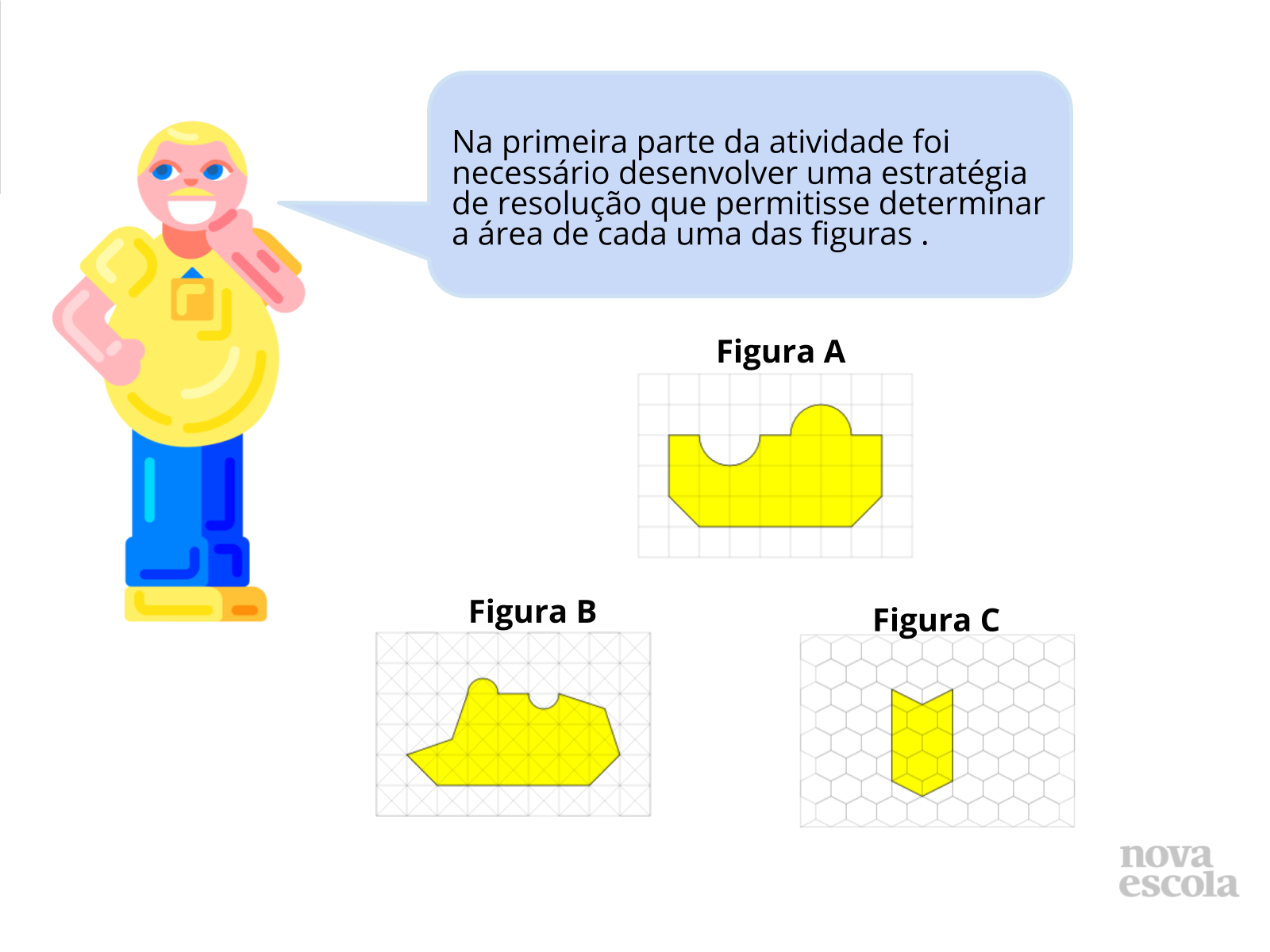
Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Discussão das soluções (parte I)

Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Discussão das soluções (parte I)
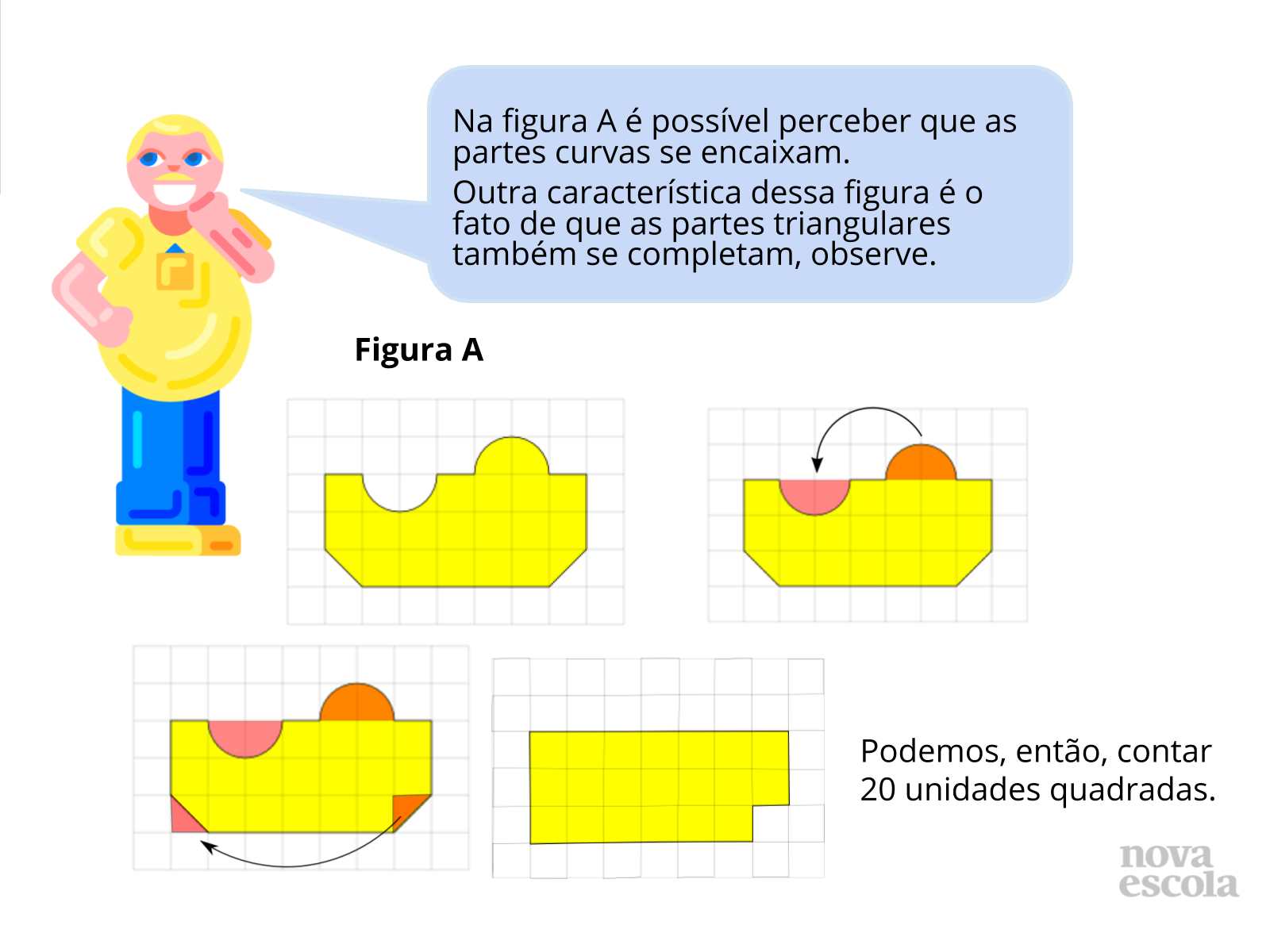
Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Discussão das soluções (parte I)
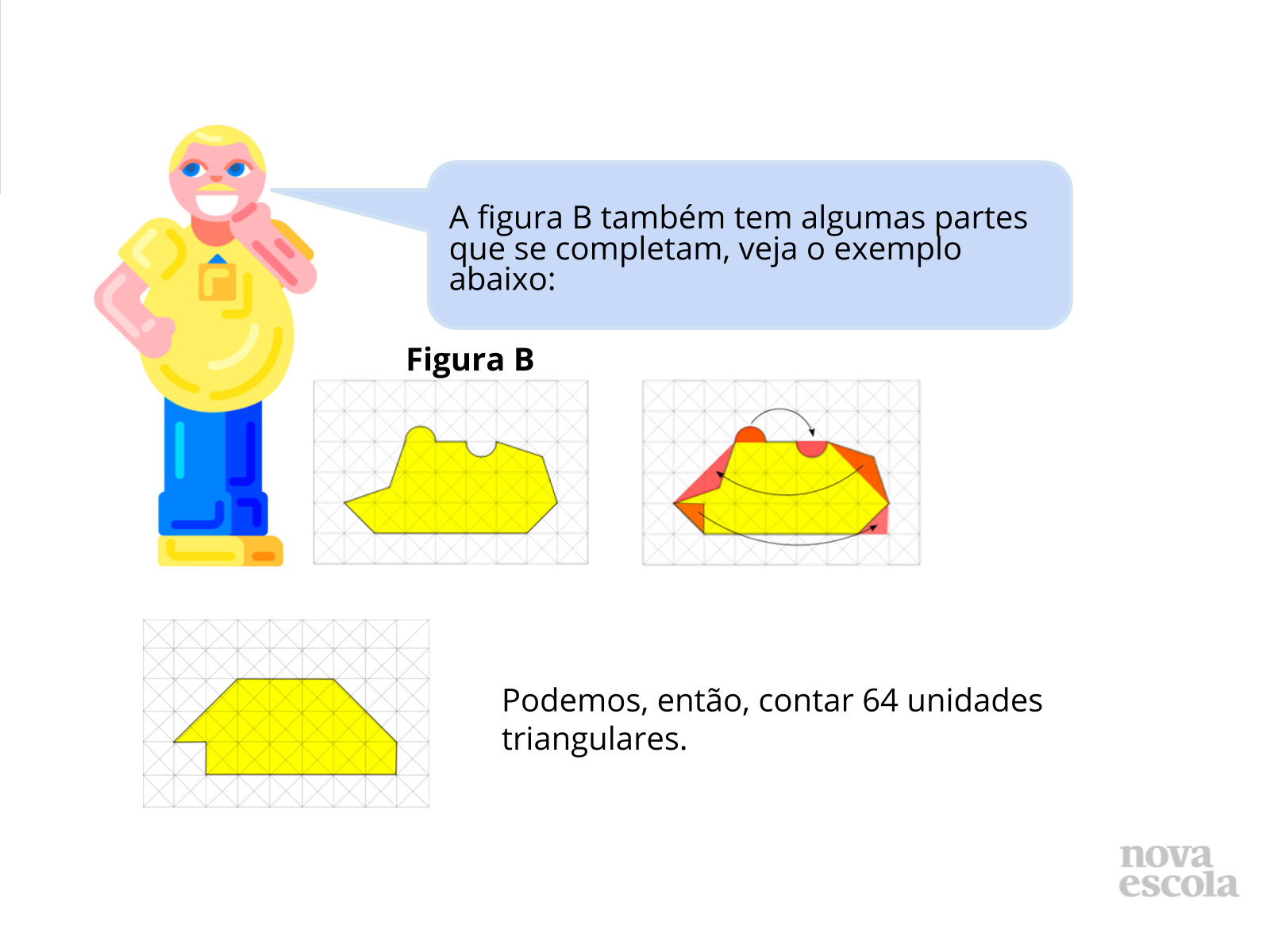
Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Discussão das soluções (parte I)
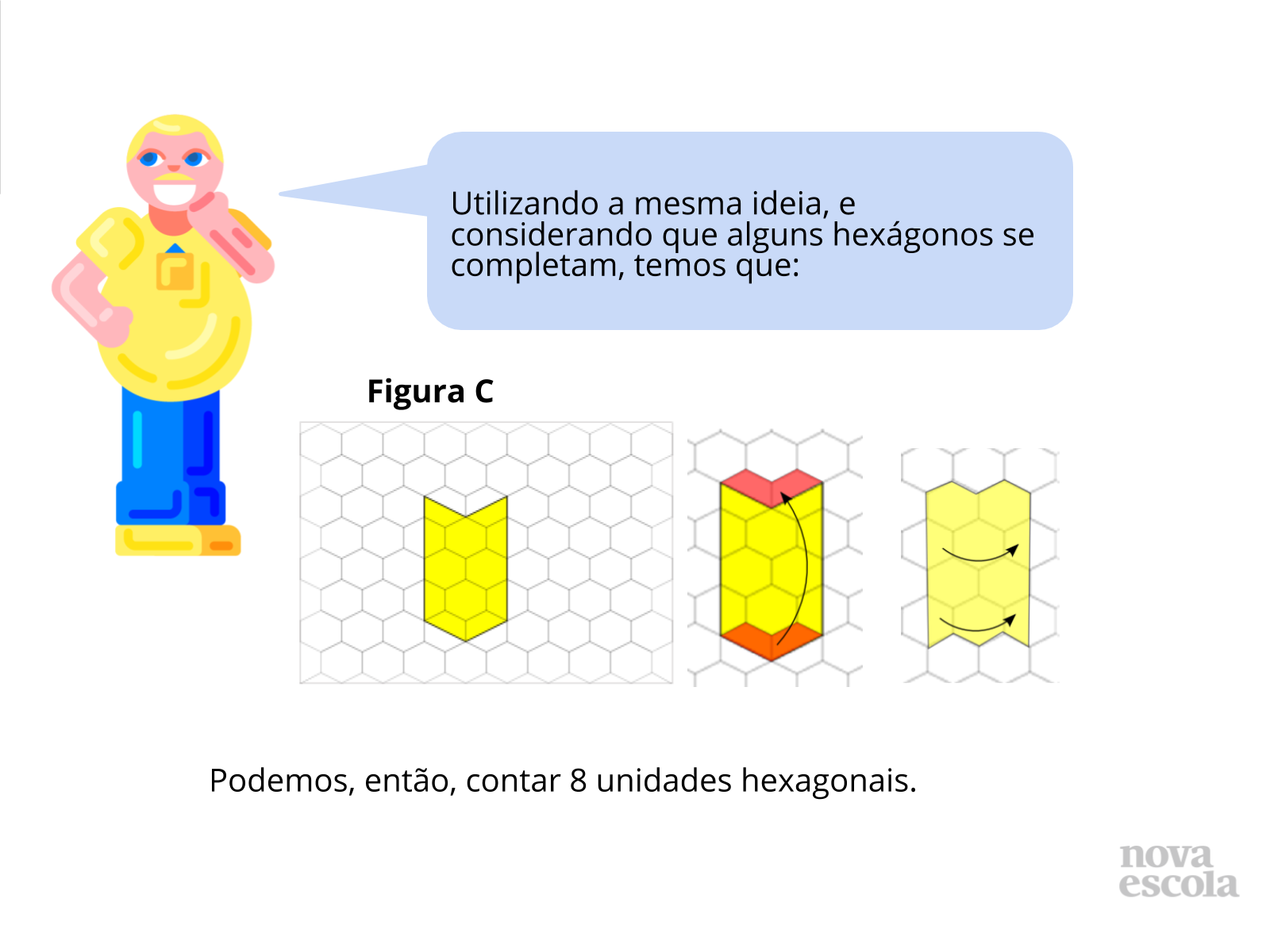
Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Discussão das soluções (parte I)

Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Discussão das soluções (parte II)

Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Discussão das soluções (parte II)
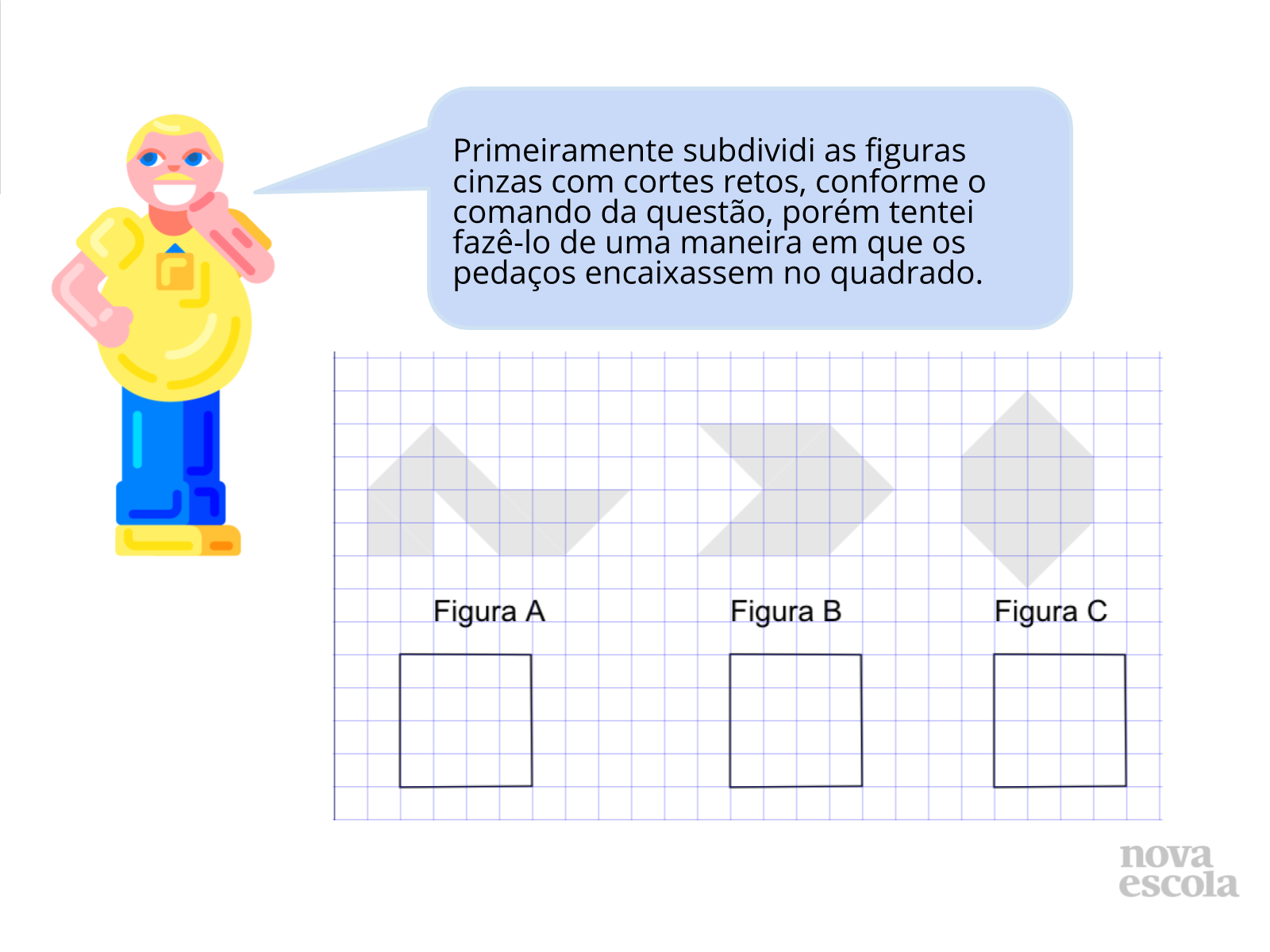
Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Discussão das soluções (parte II)
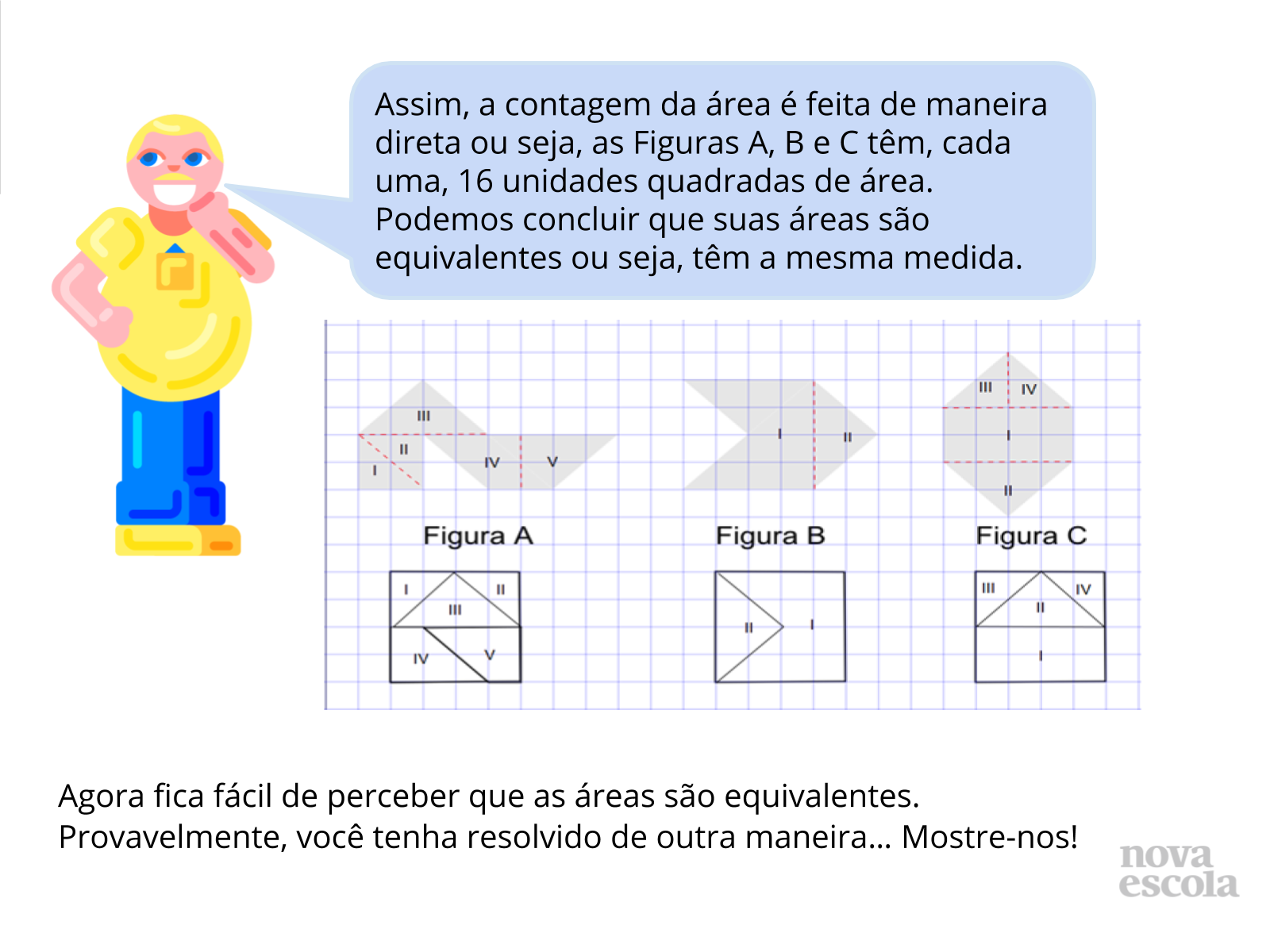
Tempo previsto: 10 minutos (slide 15 ao slide 23).
Orientações: Aqui concluímos nossa discussão d resolução mas, é importante que o professor apresente a solução como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a solução nenhuma.
Possíveis situações e dúvidas podem ser vistas no guia de intervenções.
Propósito: Provocar a discussão de soluções.
Sistematização do conceito

Tempo previsto: 3 minutos.
Orientações: Leia esta sistematização com os alunos. Se necessário, retome os slides anteriores, argumentando sobre a técnica adquirida na Atividade Principal e na importância dela na resolução de problemas de área.
Propósito: Fazer o fechamento da atividade e organizar o que foi aprendido na atividade principal.
Encerramento

Tempo previsto: 2 minutos.
Orientações: Neste momento é importante destacar o aprendizado da aula, de acordo com seu objetivo, e consolidar os conceitos utilizados.
Propósito: Reforçar o cumprimento do objetivo da aula.
Discuta com a turma:
- Em quais outras situações podem ser utilizados os conceitos e métodos, para o cálculo da área de figuras geométricas planas, desenvolvidos nesta aula?
Raio X

Tempo previsto: 10 minutos.
Orientações: Esta atividade visa avaliar a consolidação do que foi aprendido durante o desenvolvimento dessa aula, a atividade deve ser realizada individualmente.Observe como os alunos resolvem o problema, isso pode indicar se o aluno compreendeu ou não a técnica de composição e decomposição de figuras geométricas planas.
Propósito: Possibilitar um momento de reflexão e avaliação para o aluno.
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_22GRM01
Recursos
- Necessários:
- caderno
- lápis
- régua
- tesoura
- cola
- grupo de alunos no Whatsapp
- Opcionais:
- Google Sala de Aula
- Meet
- Vídeo : “Decomposição de formas para calcular a área: malhas quadriculadas” - Khan Academy, disponível em: https://www.youtube.com/watch?v=CfOS5RQE0FI acesso em 04 de jul 2020.
Para este plano, foque na etapa: Atividade Principal
Aquecimento
Sugira a visualização do vídeo “Decomposição de formas para calcular a área: malhas quadriculadas” disponível no Khan Academy.
Atividade principal
A atividade tem o intuito de promover uma retomada de conceitos relacionados ao uso de malhas para a determinação de áreas. Para isso os alunos precisam utilizar malhas quadriculadas, caso o aluno não tenha em mãos, disponibilize na Unidade Escolar o material para a retirada pelos alunos.
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Os alunos devem postar seus vídeos ou fotografias para compartilhar suas respostas em um ambiente de interação como WhatsApp ou Google Sala de Aula, por exemplo. A intenção é formar um painel de soluções e promover uma discussão rica e estimuladora entre os alunos e professor.
Raio X
A atividade do Raio X pode ser usada como tarefa de casa ou como avaliação da aula. Envie e faça a discussão da mesma forma que fez com a atividade principal. Lembre-se também que há atividades complementares que podem ser enviadas para os alunos como atividades de fixação ou sistematização.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alex de Cassio Macedo
Mentora: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF07MA26) Resolver e elaborar problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas.
Objetivos específicos
Analisar a importância das decomposições de figuras planas no cálculo de medidas de superfície (área).
Conceito-chave
Composição e decomposição de figuras planas.
Recursos necessários
- Atividades impressas em folhas.
- Régua, lápis, borracha, caderno.
- Tesoura, cola (opcional).