Resumo da aula
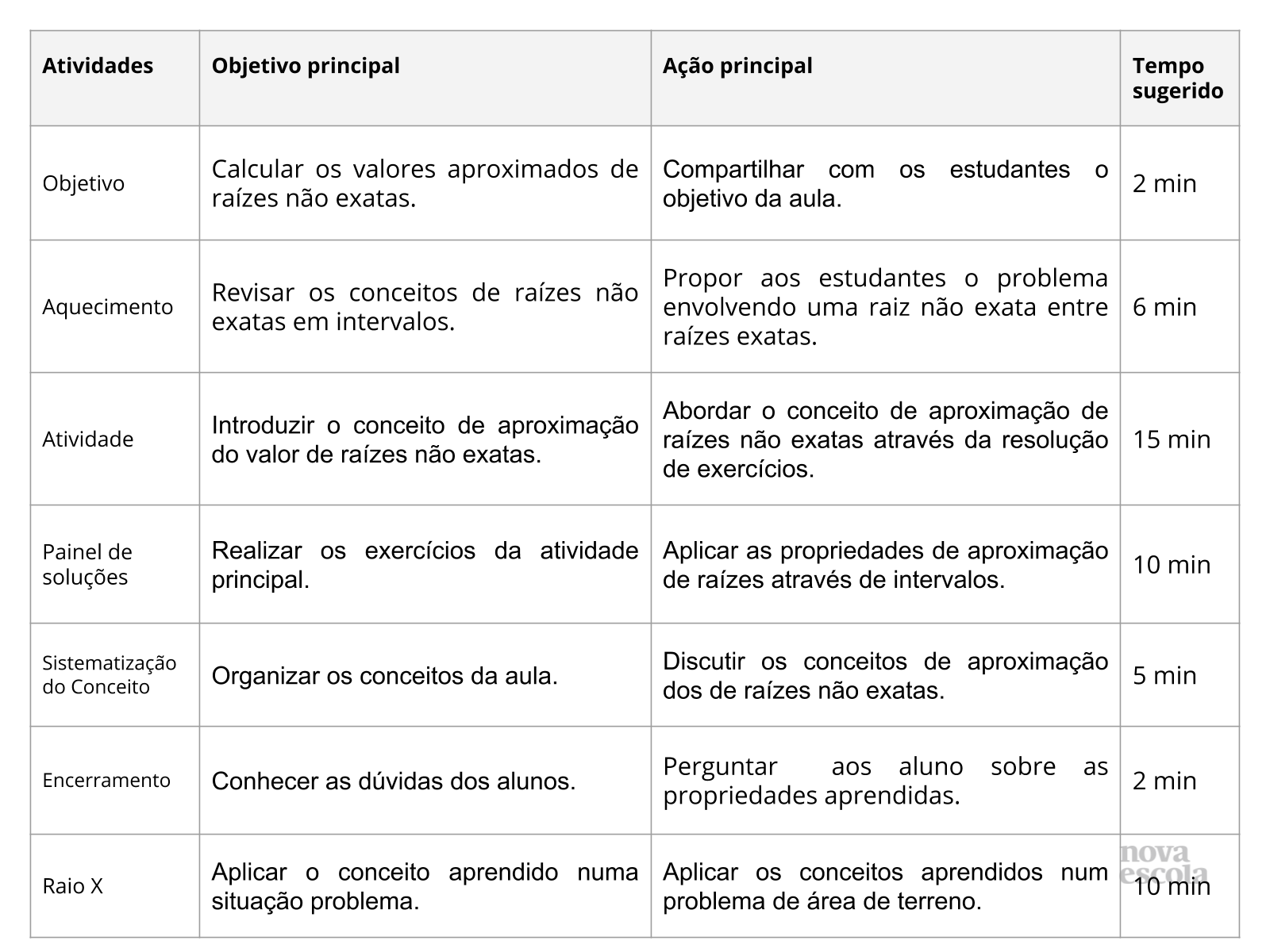
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo do plano

Tempo sugerido: 2 minutos.
Orientação: Apresente o objetivo aos alunos.
Propósito: Esclarecer os objetivos aos estudantes.
Discuta com a turma:
Aquecendo a fatoração

Tempo sugerido: 6 minutos.
Propósito: Analisar o intervalo que contém raízes não exatas.
Orientação: tratando-se de uma revisão, mostre aos alunos a ideia de se resolver através de intervalos de valores.
Discuta com a turma:
- Como encontrar os intervalos usando raízes exatas.
- Quais são as raízes exatas com valor menor ou maior que a raiz desejada.
- Como isso poderia ser representado na reta numerada?
Aquecimento
Resolução do Aquecimento
Aprendendo valor aproximado
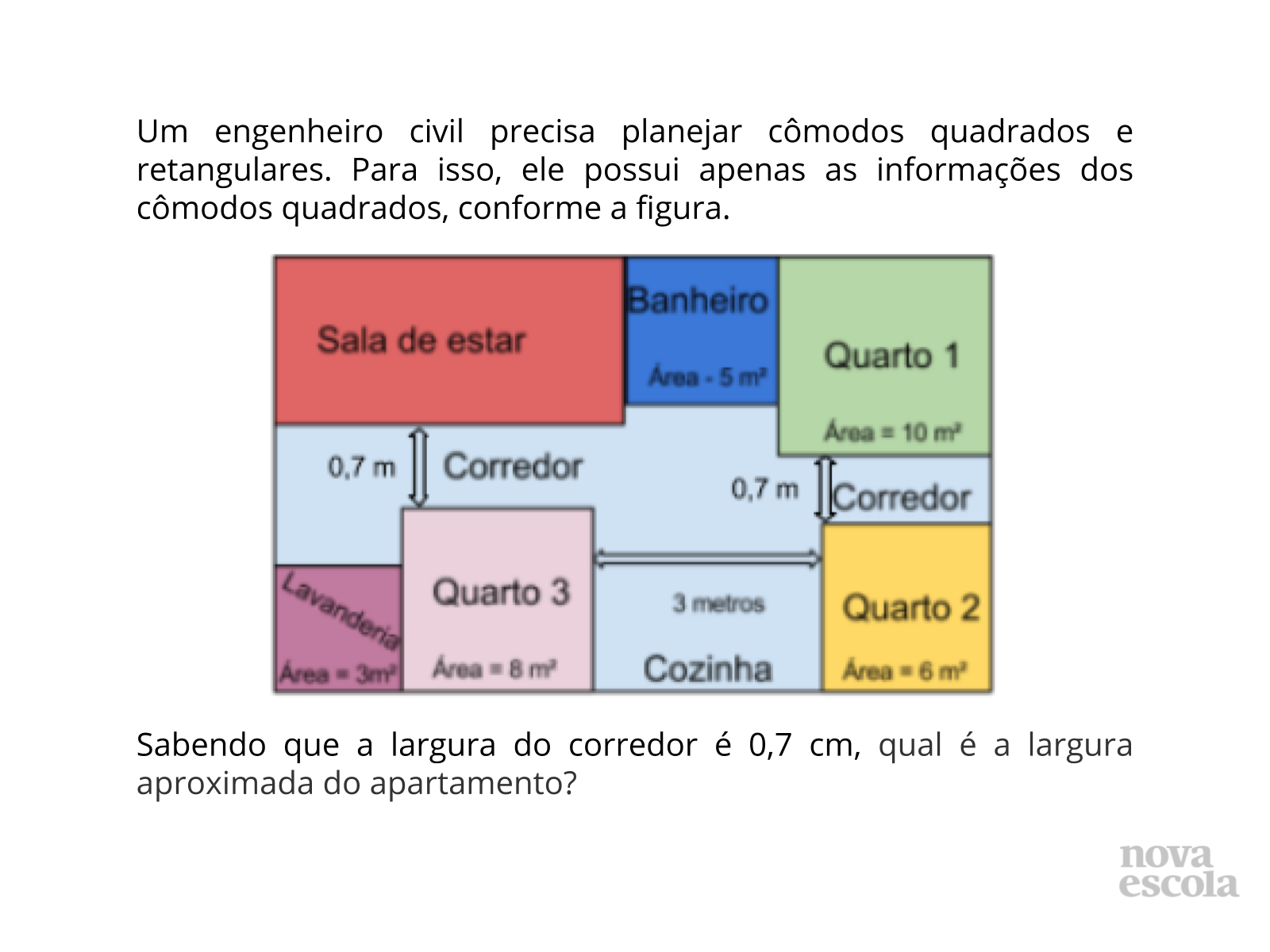
Tempo sugerido: 15 minutos.
Propósito: Problematizar a questão de valores aproximados de raízes não exatas.
Orientação: Investigar as diferentes situações que podem ocorrer, por exemplo, como os lados poderiam ser obtidos através das informações dadas. Isso será útil para perceber os padrões relacionados à atividade.
Discuta com a turma:
- Como os alunos podem descobrir a largura do apartamento?
- Há diferentes formas de medir o apartamento? Por exemplo, seria possível medir raízes não exatas com a régua?
- Termine enfatizando que alguns radicais não teriam medida exata com régua.
Percepção da aula

Tempo sugerido: 30 segundos.
Propósito: Sinalizar aos estudantes que o momento de discussão das soluções será iniciado.
Orientação: Leia para a turma com entusiasmo.
Discuta com a turma:
- Será que é possível termos várias soluções para esse problema?
1ª Parte da Resolução da atividade principal
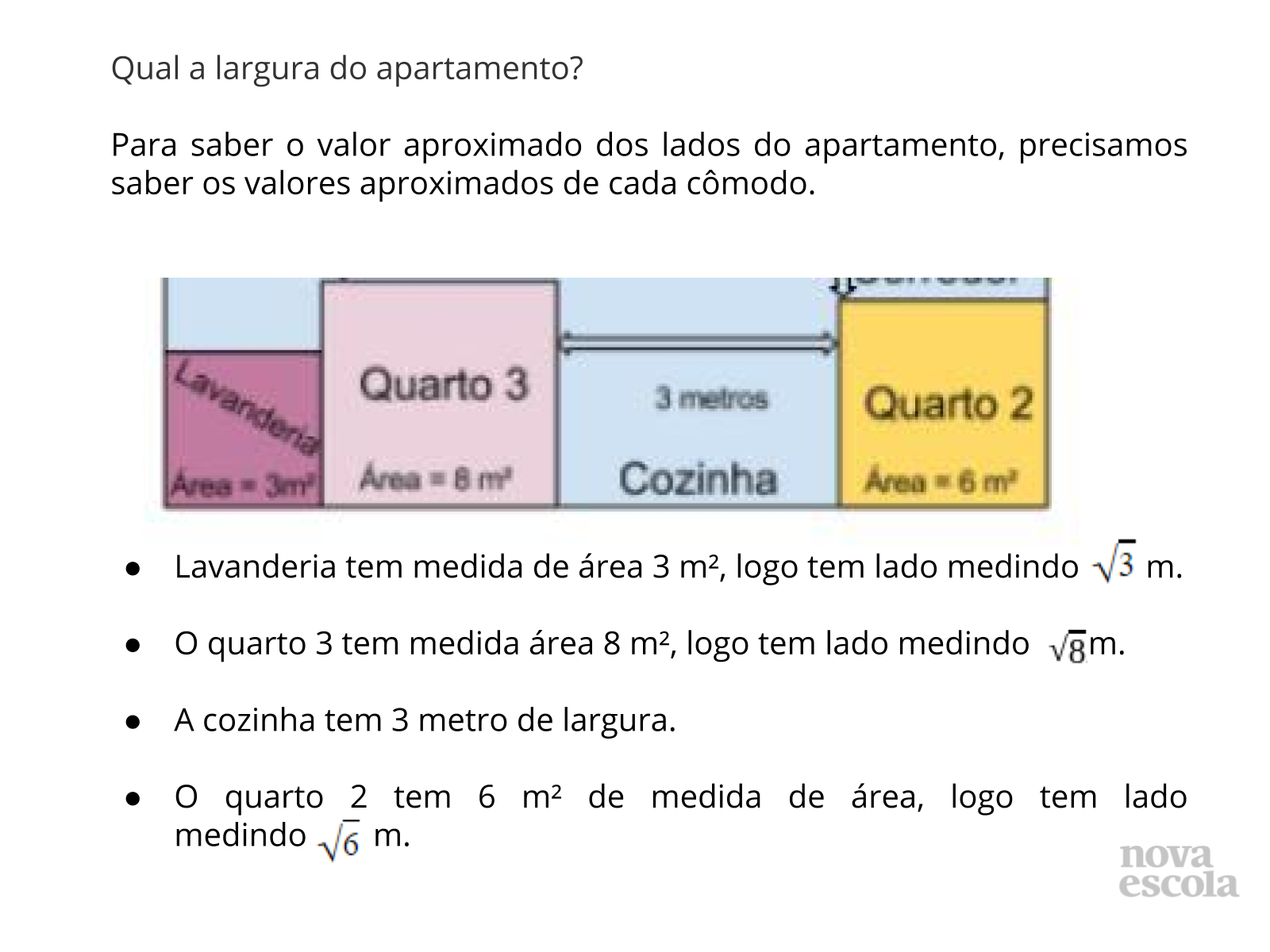
Tempo sugerido: 1 minuto e 30 segundos.
Propósito: Iniciar a solução da atividade principal.
Orientação: Mostre aos estudantes uma primeira forma de resolução. Discuta rapidamente que é interessante verificar primeiro as características de cada cômodo.
Discuta com a turma:
- Como podemos utilizar as informações obtidas?
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Explicação da localização das raízes não exatas na reta numerada
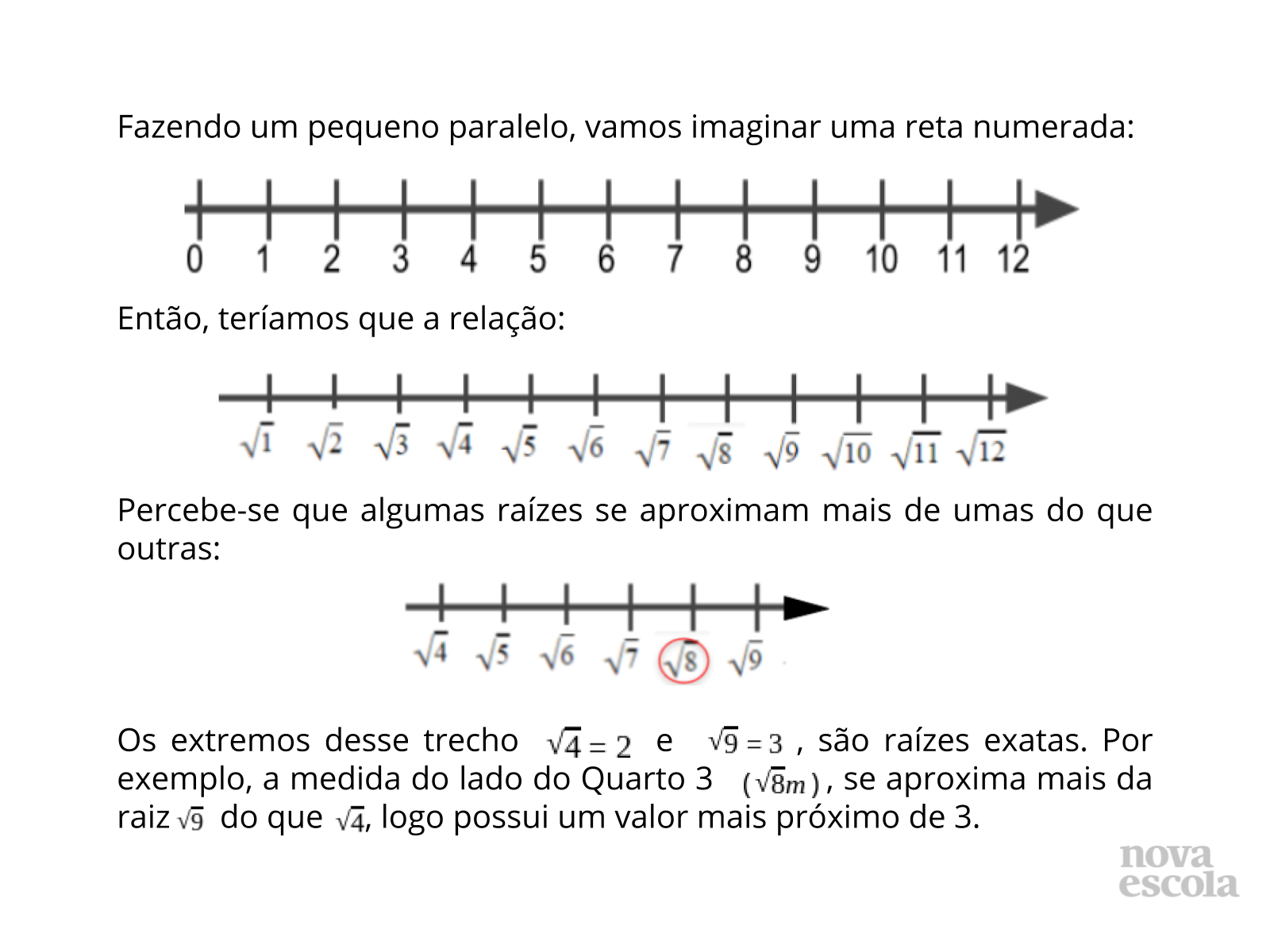
Tempo sugerido: 2 minutos.
Propósito: Rever o conceito de raízes não exatas na reta numerada.
Orientação: Mostre aos estudantes que o critério neste caso leva em consideração que se está falando da mesma reta com uma representação diferente.
Discuta com a turma:
- Como podemos comparar as duas retas?
2ª Parte da resolução da atividade principal
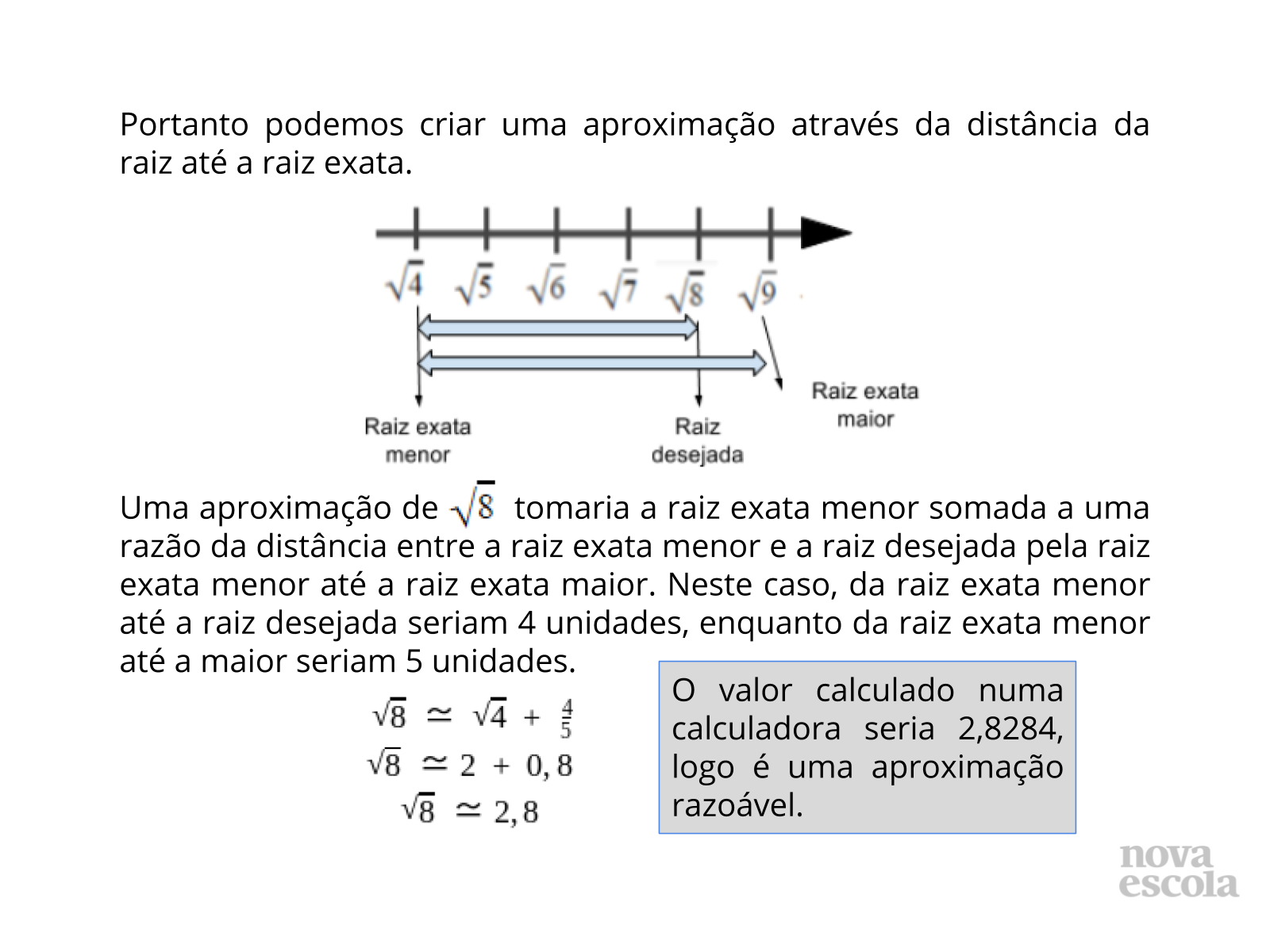
Tempo sugerido: 2 minutos.
Propósito: Fazer a correlação entre o problema proposta e a reta numerada.
Orientação: Mostre aos estudantes que a análise pode ser feita para cada radical.
Discuta com a turma:
- Como expressar o radical através de valores aproximados?
3ª Parte da resolução da atividade principal
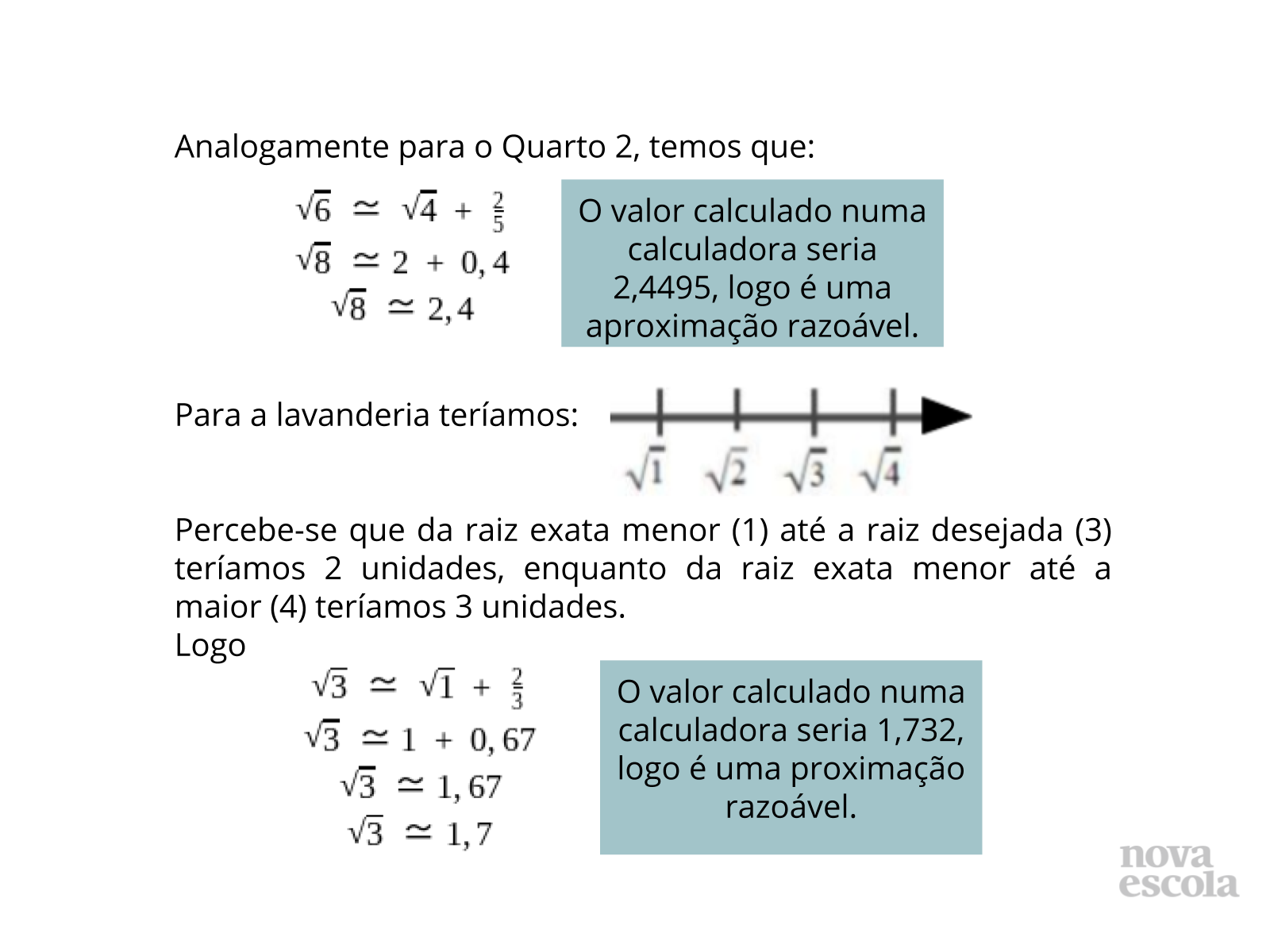
Tempo sugerido: 2 minutos.
Propósito: Continuar a resolução da atividade principal.
Orientação: Destaque aos alunos que é possível realizar a atividade sabendo as raízes exatas mentalmente. Ressalte que este processo torna-se facilitado conforme o estudante se familiarizar com as raízes.
Discuta com a turma:
- Como podemos calcular raízes não exatas?
- Explique que a diferença ficou maior pois o número de divisões feitas entre as medidas foi menor. Quanto mais divisões, como nos casos do Quarto 2 e Quarto 3, a aproximação foi melhor.
Encerramento da resolução da atividade principal

Tempo sugerido: 2 minutos.
Propósito: Concluir a resolução da atividade principal.
Orientação: Destaque aos alunos, no exercício (c), como os radicais são diferentes, pode mantê-los. No caso do (d), por serem radicais iguais, pode somá-los ou subtraí-los.
Discuta com a turma:
- Com o que podemos comparar a soma de radicais diferentes?
- Com o que podemos comparar subtração de radicais iguais?
Sistematizando os conhecimentos
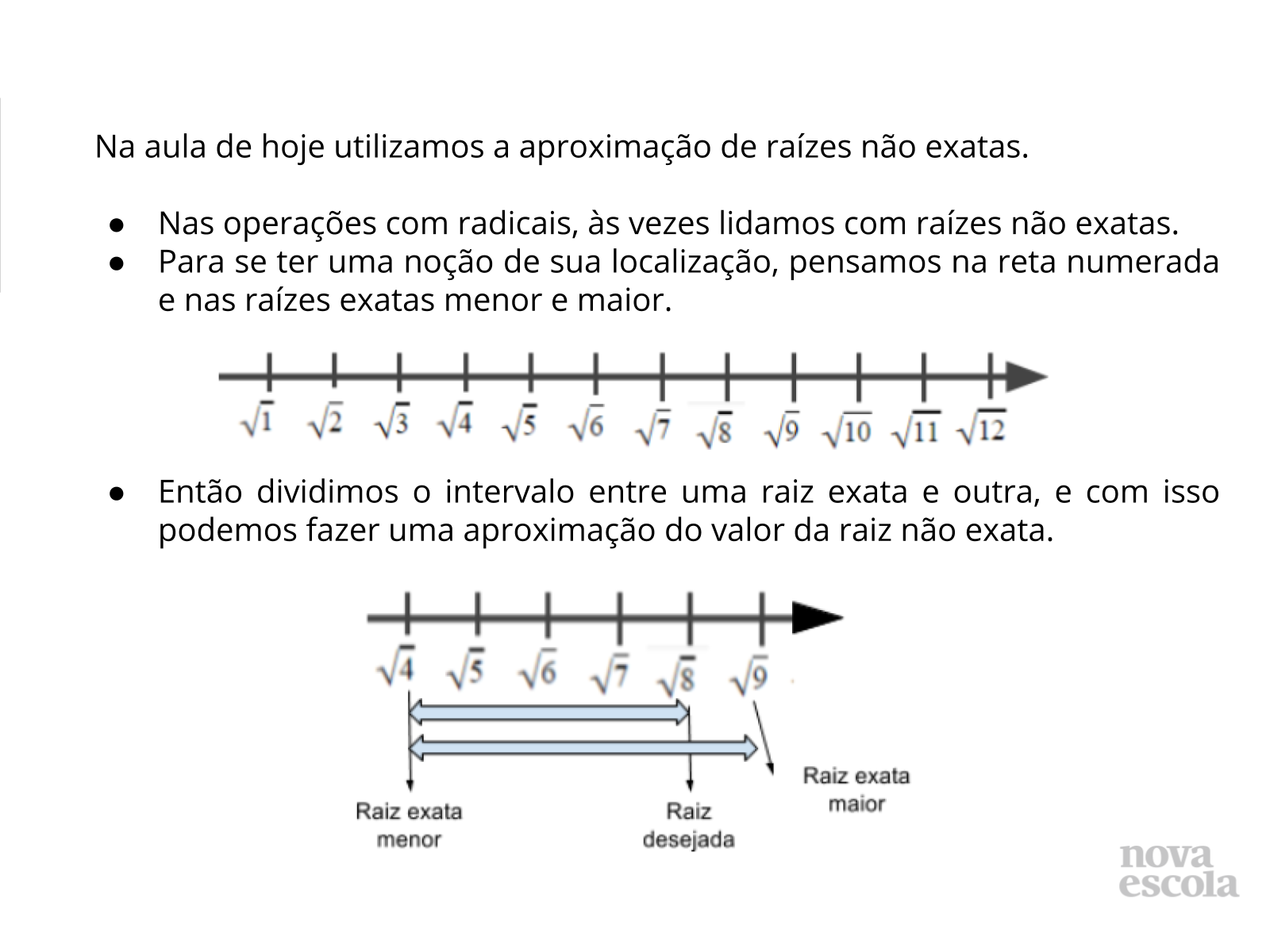
Tempo sugerido: 5 minutos.
Propósito: Sistematizar os conceitos aprendidos em aula.
Orientação: Discuta com a sala os principais tópicos, pedindo aos alunos citarem exemplos quando for possível.
Discuta com a turma:
- Poderia citar um exemplo de uma raiz não exata? Qual seu valor aproximado?
- Como realizamos a soma e subtração com raízes aproximadas?
- Para que serve a aproximação?
Encerramento da aula

Tempo sugerido: 2 minutos.
Orientação: Discuta com a sala os principais tópicos, pedindo aos alunos citarem exemplos quando for possível.
Propósito: Finalizar a aula retomando a importância do conceito estudado.
Discuta com a turma:
- Onde poderia ser aplicado a aproximação de raízes não exatas?
Raio-X do Plano de Aula
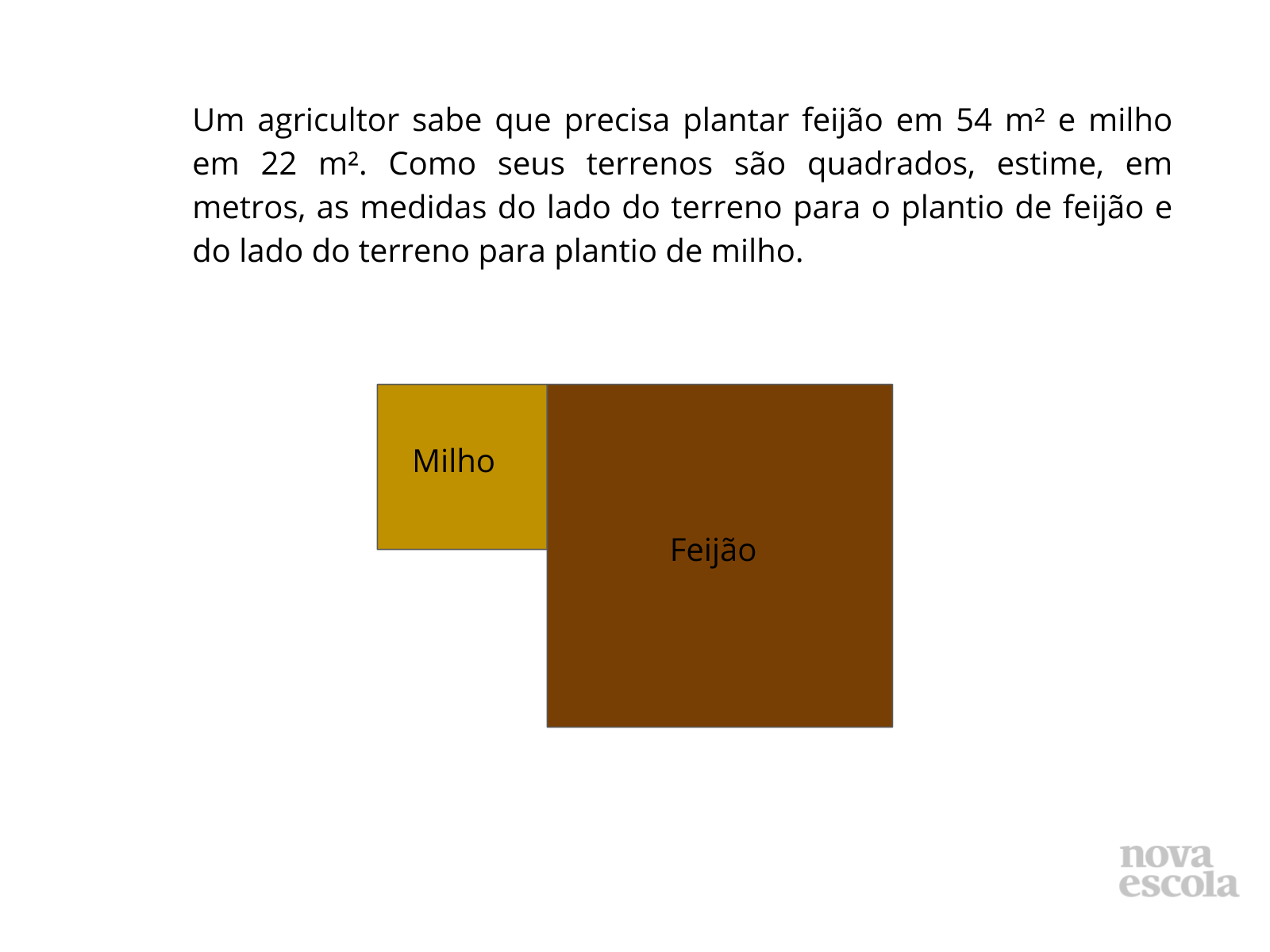
Tempo sugerido: 10 minutos.
Orientação:
Exponha aos alunos o problema. Eles terão de utilizar os conceitos aprendidos em sala. Diga que podem utilizar a ideia da reta numerada para resolver.
Discuta com a turma:
- Raízes exatas e intervalos.
- Valor aproximado de raízes não exatas.
- Adição e subtração de raízes não exatas.
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 




























