Aquecimento
Plano de Aula
Plano de aula: Divisão de racionais fracionários na prática
Plano 8 de uma sequência de 10 planos. Veja todos os planos sobre Operações com racionais
Tem interesse no tema "Neurociência, adolescências e engajamento nos Anos Finais"?
Inscreva-se neste tema para receber novidades pelo site e por email.
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Rosiane F. Prates
Mentora: Débora Vieira de Moraes
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA08 - Ampliar conceito e aplicação dos números racionais fracionários dentro do cálculo de divisão.
Conhecimentos que a turma deve dominar:
Domínio do conceito de fração, identificar a relação entre os conjuntos numéricos (racionais, inteiros e naturais); realizar adição e subtração com racionais.
(Unidade NOVA ESCOLA: MAT6_05NUM; MAT6_07NUM01; MAT7_07NUM02 e MAT7_07NUM03; Base Nacional: EF06MA06; EF06MA07; EF06MA08; EF06MA09)
Objetivos específicos
Calcular de racionais fracionários positivos e negativos
Conceito-chave
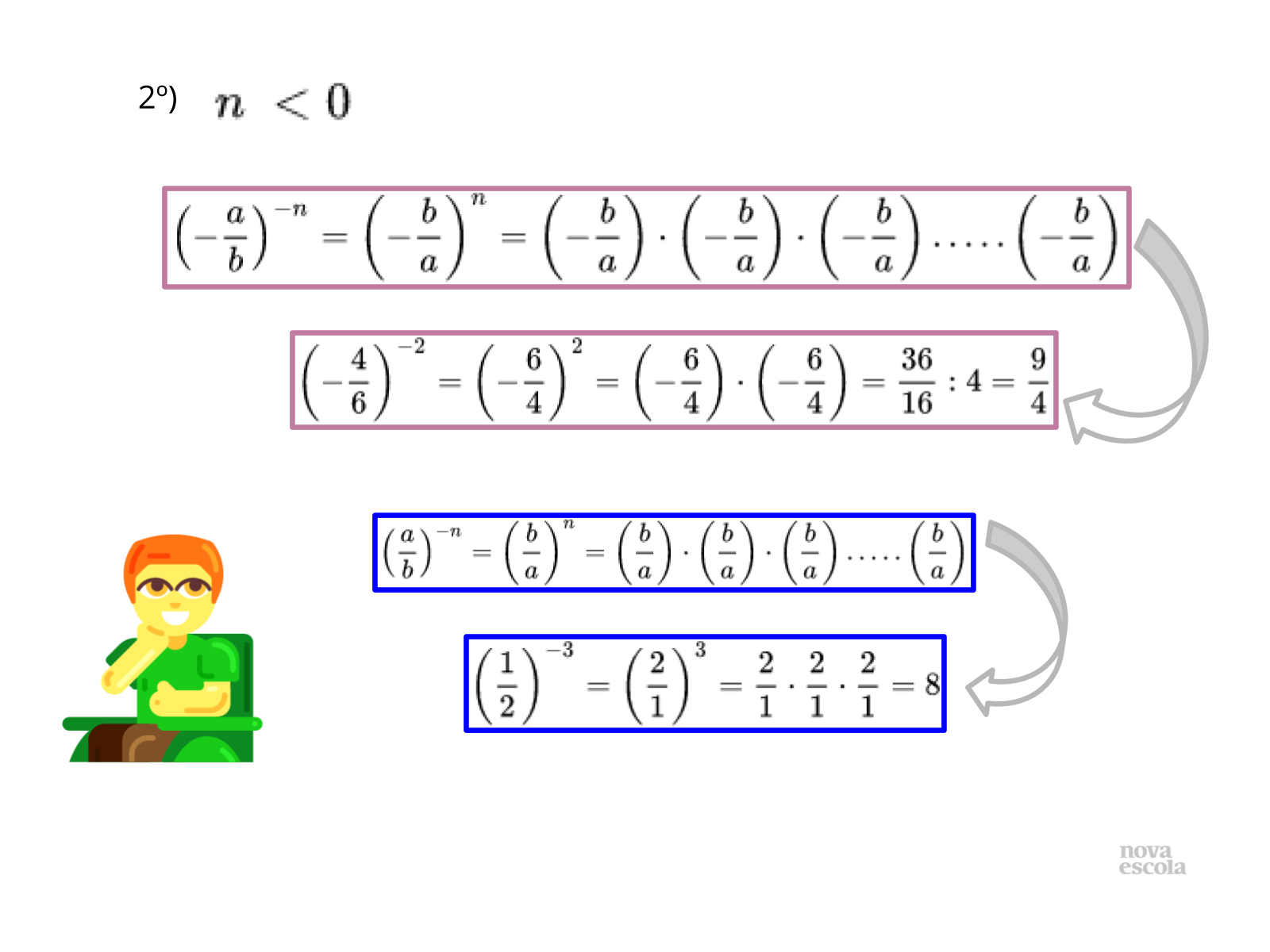
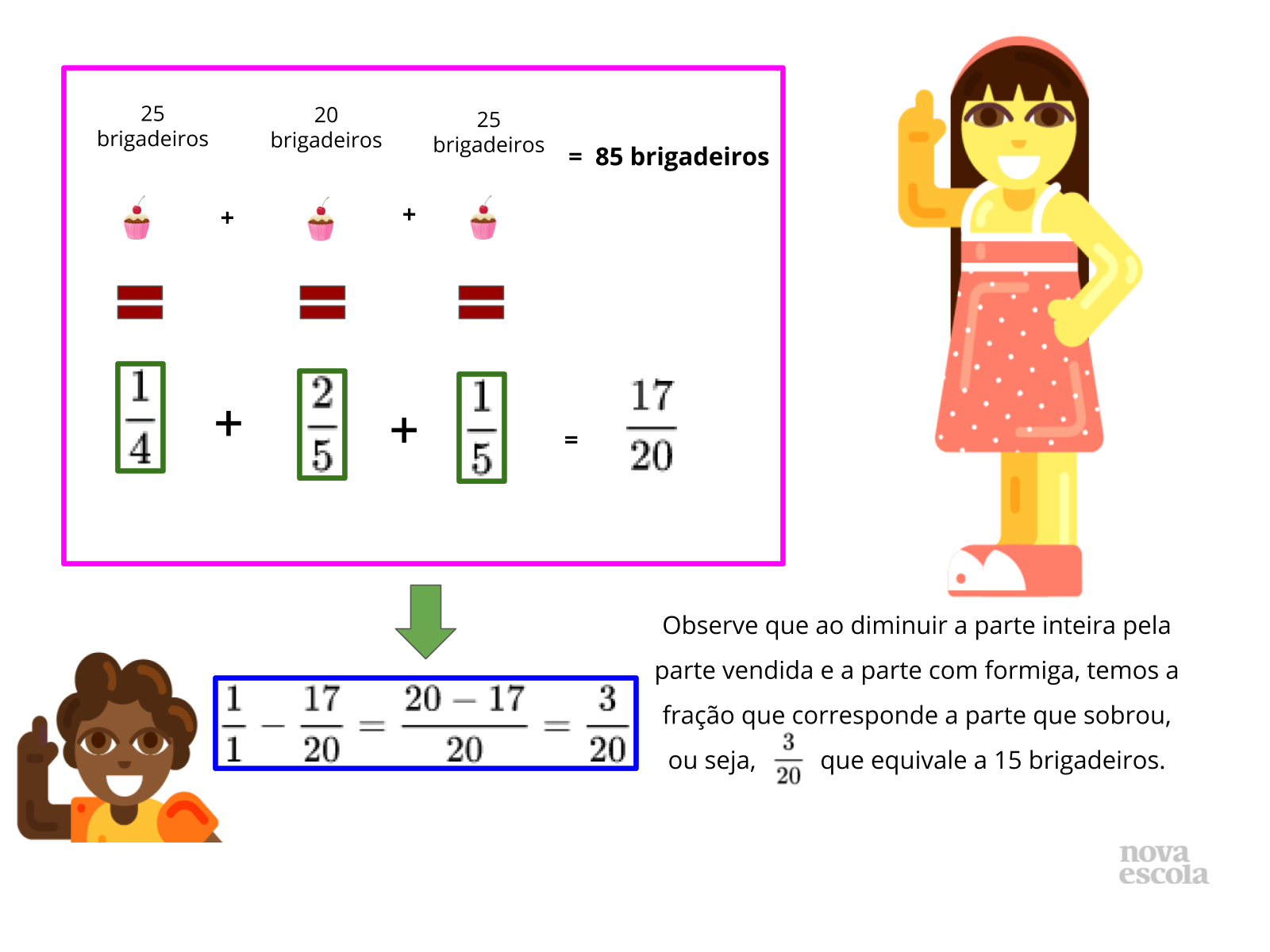
ampliar o conceito de divisão com racionais escritos na forma fracionária.
Recursos necessários
Atividades impressas em folhas, coladas no caderno ou não.
Projetor multimídia (caso não se utilize impressões).
Habilidades BNCC:
Planeje suas aulas pelo Whatsapp!
Qualidade com economia de tempo
Aula
Resumo da aula
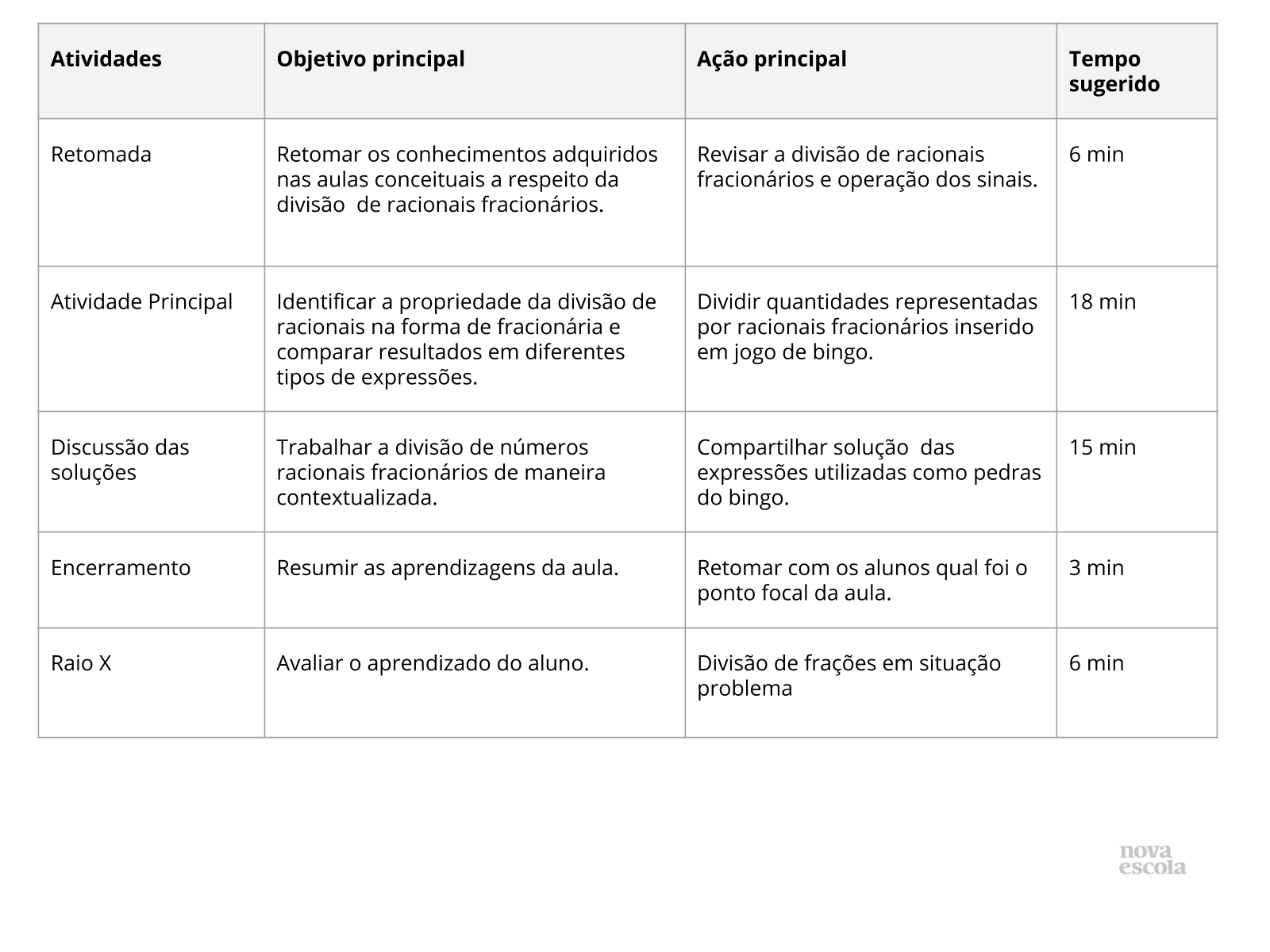
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
OBJETIVO

Tempo sugerido: 2 min
Orientações: Apresentar o objetivo da aula de maneira breve, projete ou leia o objetivo para a turma.
Propósito: compartilhar o objetivo da aula
Novo curso gratuito

Conheça nosso mais novo curso sobre adolescências, neurociência e engajamento nos anos finais
VER CURSO