Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 1 minuto.
Orientação: Projete ou escreva o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula, criando uma boa expectativa em relação ao que irão aprender durante a aula.
Aquecimento

Tempo previsto: 5 minutos.
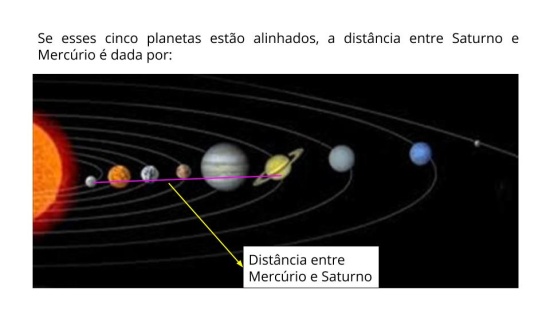
Orientações: Prepare as atividades (principal, raio X e complementares) antes da aula. Se possível, traga essas atividades impressas para os alunos, ou projete-as na lousa! Converse com seus alunos sobre comprimentos muito pequenos, como comprimento de células ou a espessura de uma folha de papel.
Propósito: Realizar, através de questões direcionadas, um levantamento dos conhecimentos prévios que os alunos possuem sobre o tema e, motivá-los a utilizar esse conhecimento para resolver a situação problema proposta.
Discuta com a turma:
- O que é um comprimento muito curto?
- A espessura da representação de uma reta feita com a caneta é muito pequeno?
- Um fio de cabelo tem uma espessura muito pequena?
- E as células que compõem o fio de cabelo, são muito pequenas?
- Qual a menor unidade de comprimento que conhecemos até o momento? (Relembre a sequência: km hm dam m dm cm mm …)
Atividade principal

Tempo sugerido: 15 minutos (Slides 4 a 7).
Orientações: Divida os alunos em duplas. Agrupe alunos com níveis de proficiências próximos (não iguais) para que um ajude o outro. Solicite que os alunos façam a leitura e análise do problema individualmente nas duplas. Nesse momento, as duplas já podem trocar informações/ideias de resolução e conhecimentos prévios que eles possuem. Solicite que eles grifem/destaquem no texto do problema, palavras-chaves que auxiliarão na resolução dos itens e, tentem resolver o problema em duplas. Permeie entre as carteiras e observe se algum aluno não está realizando a atividade. Aproveite esse momento para intervir e fazer registros das dificuldades que forem surgindo. No momento da socialização do problema, procure abordar (sem expor os alunos) essa(s) dificuldade(s). Após isso, peça que comparem suas soluções com as de outros colega. Escolha um aluno/dupla para socializar as respostas de cada item do problema.
Propósito: Fazer com que os alunos se apropriem do conhecimento de unidades de medidas de comprimento menores que o milímetro, como por exemplo o micrômetro e, utilize-a para calcular um comprimento muito pequeno. Posteriormente, o aluno deverá comparar essa medida com um comprimento do seu conhecimento.
Discussão de soluções

Tempo sugerido: 17 minutos (Slides 5 a 7).
Orientações: Depois que os alunos compartilharam suas estratégias, passe para esta série de slides (slides de 5 a 7) destacando algumas possíveis soluções dos itens a), b) e c) do problema.
No item a), os alunos deverão transformar 1 µm em metro. Para isso, ele deverá relacionar as informações do enunciado, onde é informado que 1 µm é a milésima parte de 1 mm. Assim como 1 mm é a milésima parte de 1m, o aluno precisa concluir que 1 µm é a milésima da milésima parte de 1 m, ou seja, 1 µm é igual a 1 milionésimo do metro. Professor, permeie pelas carteiras e observe se os alunos estão aplicando ou discutindo essas relações. Aproveite para fazer registros dos alunos que apresentam dificuldade quanto a essa interpretação do problema. Os alunos ainda poderão resolver esse item utilizando uma Regra de Três.
Propósito: Fazer com que os alunos se apropriem do conhecimento de unidades de medidas de comprimento muito curtas (o micrômetro), menores que o milímetro, é muito importante para o nosso cotidiano.
Discuta com a turma:
- Quanto é um milésimo?
- Quanto é um milésimo de um milésimo? (Professor, o aluno precisa compreender que existe a operação multiplicação envolvida nessa questão)
- Quanto vale mil milésimos? Quanto vale mil milímetros?
Discussão de soluções

Tempo sugerido: 17 minutos (Slides 5 a 7).
Orientações: Depois que os alunos compartilharam suas estratégias, passe para esta série de slides (slides de 5 a 7) destacando algumas possíveis soluções dos itens a), b) e c) do problema.
No item b), primeiramente o aluno precisa observar que se o comprimento dado está aumentado em 400 vezes, logo, para obter o comprimento real ele precisa dividir o valor dado (10 cm) por 400. Professor, permeando entre as carteiras, observe se algum aluno utilizou outra estratégia e se os alunos compreenderam essa primeira passagem. Observe ainda se os alunos estão atentos à unidade de medida, que nesse caso, o comprimento real estará (ainda) em centímetro. Finalmente, o aluno precisa converter a medida encontrada na divisão para micrômetro. O aluno poderá facilmente fazer isso utilizando um Regra de Três. Porém, nesse momento, o aluno precisa transformar 1 µm em centímetro. Professor, fique atento nesse momento. Observe se os alunos estão fazendo essa conversão corretamente e observe ainda se os alunos visualizaram que as grandezas envolvidas nessa Regra de Três são micrômetro e centímetro. Se algum aluno está utilizando uma estratégia diferente dessa, peça para ele socializá-la com a classe.
Aproveite para fazer registro das dificuldades encontradas nesse item e, sem expor o(s) aluno(s), levante todas essas dificuldades na socialização.
Propósito: Compreender que um comprimento aumentado 400 vezes (por exemplo), para se obter o comprimento real é necessário dividi-lo por 400. Realizar conversões entre medidas de comprimento envolvendo o micrômetro.
Discuta com a turma:
- Se uma medida foi aumentada duas vezes, o que devemos fazer para retornar à medida original?
- Qual é a operação inversa da multiplicação?
- 1 µm é mil vezes menor que 1 mm, e 1 cm é dez vezes menor que 1 mm, então, 1 µm é quantas vezes menor que 1 cm? Quanto isso equivale em cm?
Discussão de soluções

Tempo sugerido: 17 minutos (Slides 5 a 7).
Orientações: Depois que os alunos compartilharam suas estratégias, passe para esta série de slides (slides de 5 a 7) destacando algumas possíveis soluções dos itens a), b) e c) do problema.
No item c), primeiramente o aluno precisa determinar quantas células cabem enfileiradas dentro de um grão de arroz. Para isso, o aluno poderá utilizar uma Regra de Três, onde as grandezas envolvidas são Quantidade de Células e Milímetro. Professor, fique atento para ver se os alunos estão determinando os valores corretos para serem distribuídos na Regra de Três. Como os alunos já possuem o comprimento da célula em micrômetro, eles deverão converter esse valor para milímetros, já que o comprimento dado do grão de arroz está em milímetro. É claro que existem outras resoluções, outras conversões. Caso seus alunos realizem algum processo diferente, por favor, peça para ele socializar com a classe.
Propósito: Compreender que o micrômetro é uma unidade de comprimento muito importante e saber utilizá-la na comparação de comprimentos conhecidos, como um grão de arroz, por exemplo.
Discuta com a turma:
- Quantos micrômetros tem 1 milímetro?
- 250 micrômetros cabem quantas vezes em 1 milímetro?
- 1 micrômetro é quantas vezes menor que 1 milímetro? Qual a operação a ser feita para converter uma medida de micrômetro para milímetro?
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes que o micrômetro é uma unidade de medida de comprimento utilizada para distâncias muito curtas. Reforce (muito) com seus alunos que 1 µm é a milionésima parte do metro, ou seja, 1 µm = 10-6 m. Mobilize seus alunos a resolverem a Atividade Raio X e as Atividades Complementares. Ressalte a importância do estudo contínuo, em busca do aprofundamento dos conhecimentos, fora do ambiente escolar.
Propósito: Retomar a aprendizagem da aula.
Raio X

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. Professor, utilize esse momento para avaliar o aprendizado da turma referente a esse tema. Observe se eles estão aplicando a Regra de Três adequadamente, ou se estão utilizando outra estratégia. Faça registro das dificuldades observadas para, posteriormente, serem sanados através de outras atividades diferenciadas e com outras abordagens.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante, ou seja, se utilizam os conhecimentos prévios para resolver um problema onde está envolvida uma distância muito curta, e posteriormente comparar com uma distância do seu cotidiano.