Atividade principal
Plano de Aula
Plano de aula: Jogo Com Ábaco
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Princípios do sistema de numeração decimal
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Eliane Barreto Maia Santos
Mentor: Carina Espirito Santo
Especialista de área: Luciana Maria Tenuda de Freitas
Habilidade da BNCC
(EF02MA01) Comparar e ordenar números naturais (até a ordem de centenas) pela compreensão de características do sistema de numeração decimal (valor posicional e função do zero).
Objetivos específicos
Compreender os princípios do sistema de numeração decimal: formação da centena (10 dezenas) e o valor posicional dos algarismos no número, relação entre as ordens que compõem o número.
Conceito-chave
Sistema de numeração decimal - ordens e classes
Recursos necessários
- Lápis,
- borracha,
- folha com atividades,
- ábacos e dados.
Habilidades BNCC:
Objetivos de aprendizagem
Compreender os princípios do sistema de numeração decimal: formação da centena (10 dezenas) e o valor posicional dos algarismos no número, relação entre as ordens que compõem o número.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.
Aula
Tabela de Resumo
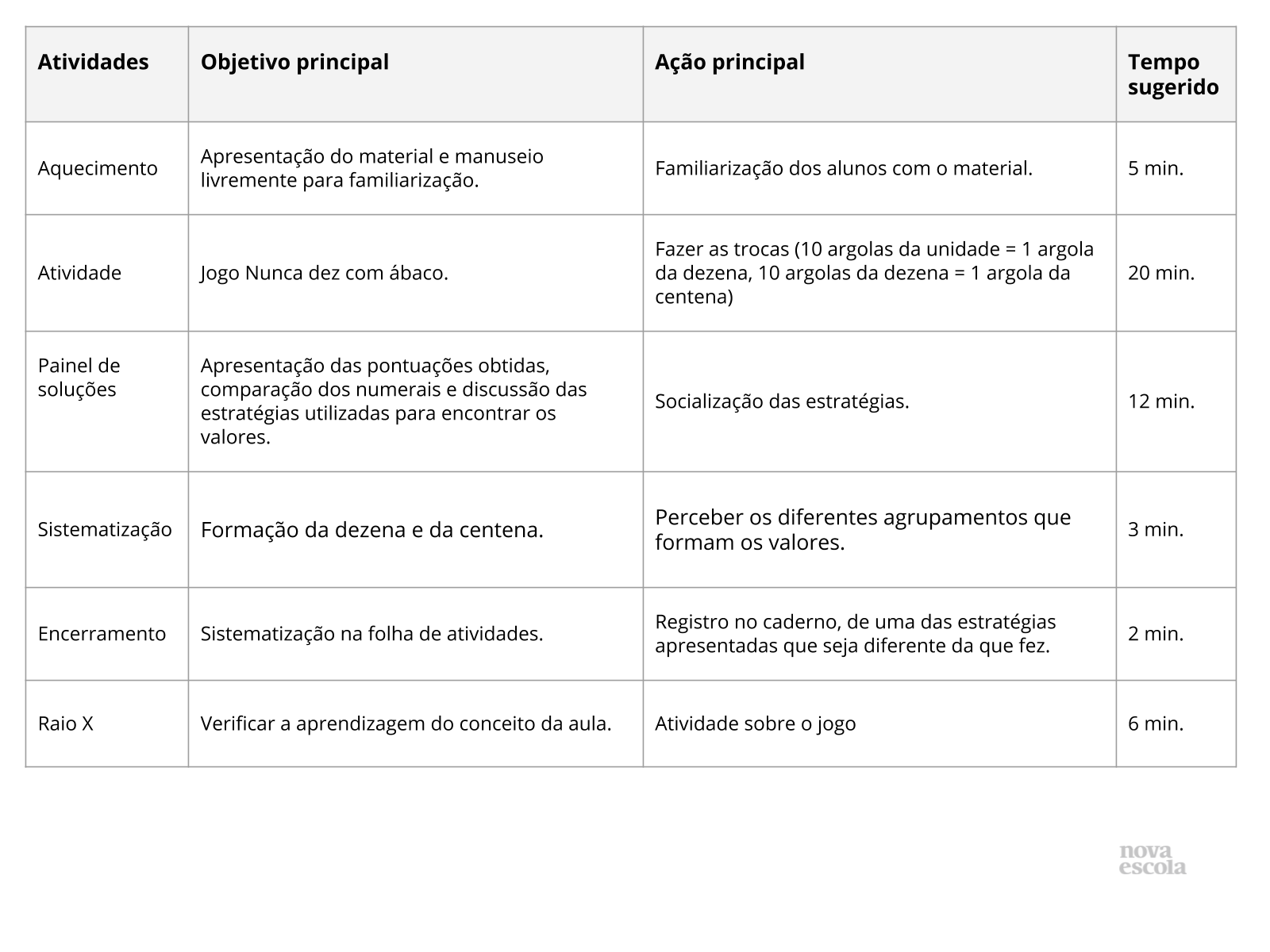 Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações: Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo estimado: 2 minutos
Orientações para o professor:
- Ler com a turma o objetivo da aula e refletir sobre o significado, perguntando “Quem entendeu o que o objetivo quer dizer?”
- Professor(a) deve explicar que:
- Assim como a linguagem escrita tem regras que precisamos seguir para formar uma palavra (organização das letras que formarão palavras, que formarão frases, que transmitirão uma informação), na matemática também temos regras que organizam os números; nos números temos os algarismos que o formam, cada um com um valor conforme a posição (a ordem) que ocupa, se o algarismo 4, por exemplo.
- Conversar com as crianças dizendo: “Se o algarismo estiver na ordem das unidades, seu valor será 4, por exemplo, mas se estiver na ordem das dezenas valerá ___ (deixar que os alunos completem a frase), porém se o algarismo estiver na ordem das centenas, valerá _____ (esperar que respondam, se não souberem, retomar o trabalho com material dourado)”.
- Assim, o(a) professor(a) já consegue coletar os conhecimentos prévios que os alunos têm acerca do tema.
Propósito: Apresentar o objetivo da aula aos alunos.
Um novo aliado para Professores Alfabetizadores

Acompanhe o progresso dos alunos durante o ano e otimize seu planejamento
ACESSAR AGORA















