Objetivo
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Joel Luiz Pereira
Mentor: Débora Vieira de Moraes
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
EF07MA07 - Comparar e ordenar números racionais em diferentes contextos e associá-los a pontos na reta numérica.
Conhecimentos que a turma deve dominar:
- Dominar o do conceito de fração e entender sua relação com números decimais; Dominar a comparação entre frações positivas (Unidade NOVA ESCOLA: MAT6_05NUM; Base Nacional: EF06MA06; EF06MA07; EF06MA08;EF06MA09).
- Dominar a comparação entre números racionais na forma decimal (Unidade NOVA ESCOLA: MAT6_01NUM; Base Nacional: EF06MA01; EF06MA02)
- Dominar a comparação entre números inteiros (Unidade NOVA ESCOLA: MAT7_03NUM; Base Nacional: EF07MA03)
Objetivos específicos
- Comparar números fracionários, inclusive com denominadores diferentes
- Comparar números decimais, inclusive com casas decimais diferentes
- Comparar números fracionários e decimais em sua forma negativa e positiva.
- Ordenar números racionais
Conceito-chave
Comparação de números racionais. Ordenação de números racionais.
Recursos necessários
- Atividades impressas em folhas, coladas no caderno ou não.
- Projetor multimídia (caso não se utilize impressões)
Tempo sugerido: 2 minutos.
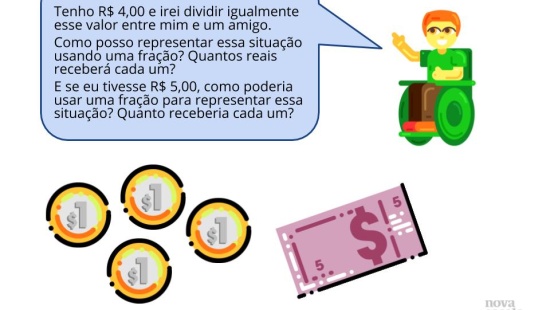
Orientação: Projete ou leia o objetivo para a turma, informando aos alunos que irão se deparar, durante a aula, com situações que possibilitarão saber se um número racional é maior ou menor do que outro.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
Tempo sugerido: 5 minutos.
Orientação: Leia o exercício ou permita que os alunos o leiam e, após um breve momento de tentativa de resolução, peça para que levantem as mãos aqueles que gostariam de responder. Oriente as discussões em sala utilizando o tópico “Discuta com a turma”. Tenha certeza de que os alunos relembrem que, para comparar frações, podem encontrar frações equivalentes ou transformá-las em números decimais. Por sua vez, para comparar números decimais, primeiramente comparamos a parte inteira e, após, a parte dos décimos, centésimos e milésimos, respectivamente. Por fim, para comparar números inteiros, os números negativos sempre serão menores do que os positivos e, ao comparar dois números negativos, o menor sempre será aquele que estiver mais distante do origem (zero).
Propósito: Relembrar comparações de números fracionários positivos e de números inteiros.
Discuta com a turma:
- O que posso fazer para comparar frações?
- Como posso comparar números decimais?
- Quando comparo um número negativo com um número positivo, qual deles será o menor? Por quê?
- Quando comparo dois números negativos, qual deles será o menor? Por quê?
Solução da atividade:
a) 5 < 10 b) 5/7 > 2/7 c) 3/6 > 5/12 d) -8 < 2 e) -4 > -7 f) 5,32 < 7,1
Atividade principal
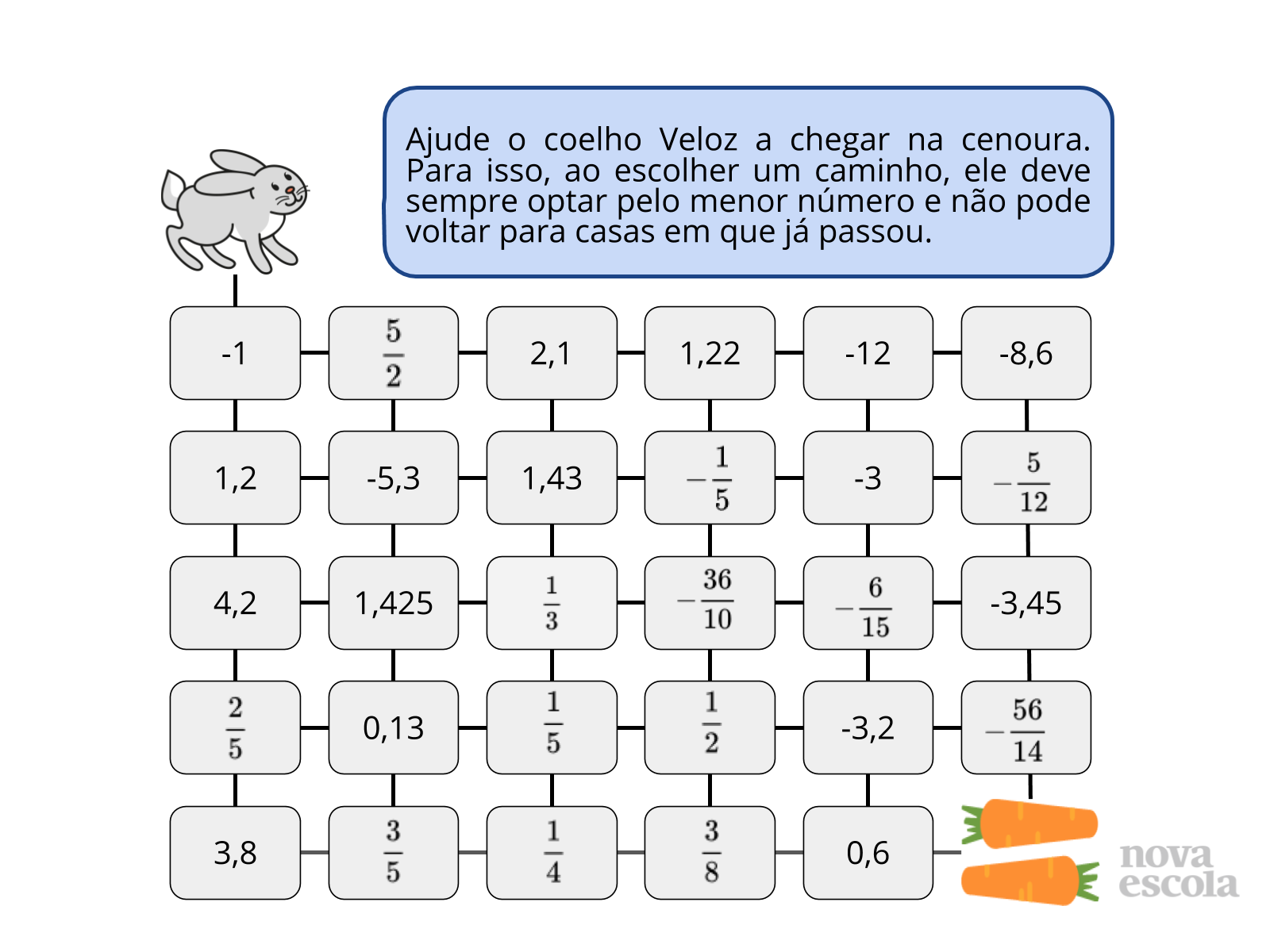
Tempo sugerido: 13 minutos.
Orientação: Entregue para cada aluno a atividade impressa, para que eles possam testar as alternativas. Após 5 minutos de primeira interação com a atividade, permita que os alunos, em duplas, discutam seus caminhos. Neste momento, circule pela sala, analisando quais são as estratégias utilizadas e fazendo intervenções.
Utilize o guia de intervenções para analisar as dificuldades e realizar intervenções.
Propósito: Possibilitar a comparação de números racionais, sendo eles fracionários (com denominadores iguais ou diferentes) ou decimais (com uma ou mais casas decimais).
Material complementar:
- Previamente, como sugestão, você pode pedir para que seus alunos com acesso à internet relembrem algumas comparações de números inteiros através do site Khan Academy.
Atividade principal parte II
Tempo sugerido: 5 minutos.
Orientação: Após os alunos terem chegado a uma solução do caminho, peça para que eles coloquem em ordem crescente os números selecionados pelo caminho do coelho. Neste momento, circule pela sala fazendo intervenções.
Você pode fazer o download desta atividade para imprimir para os seus alunos aqui.
Propósito: Possibilitar a ordenação de números racionais, inclusive em sua representação negativa.
Discussão das soluções parte I
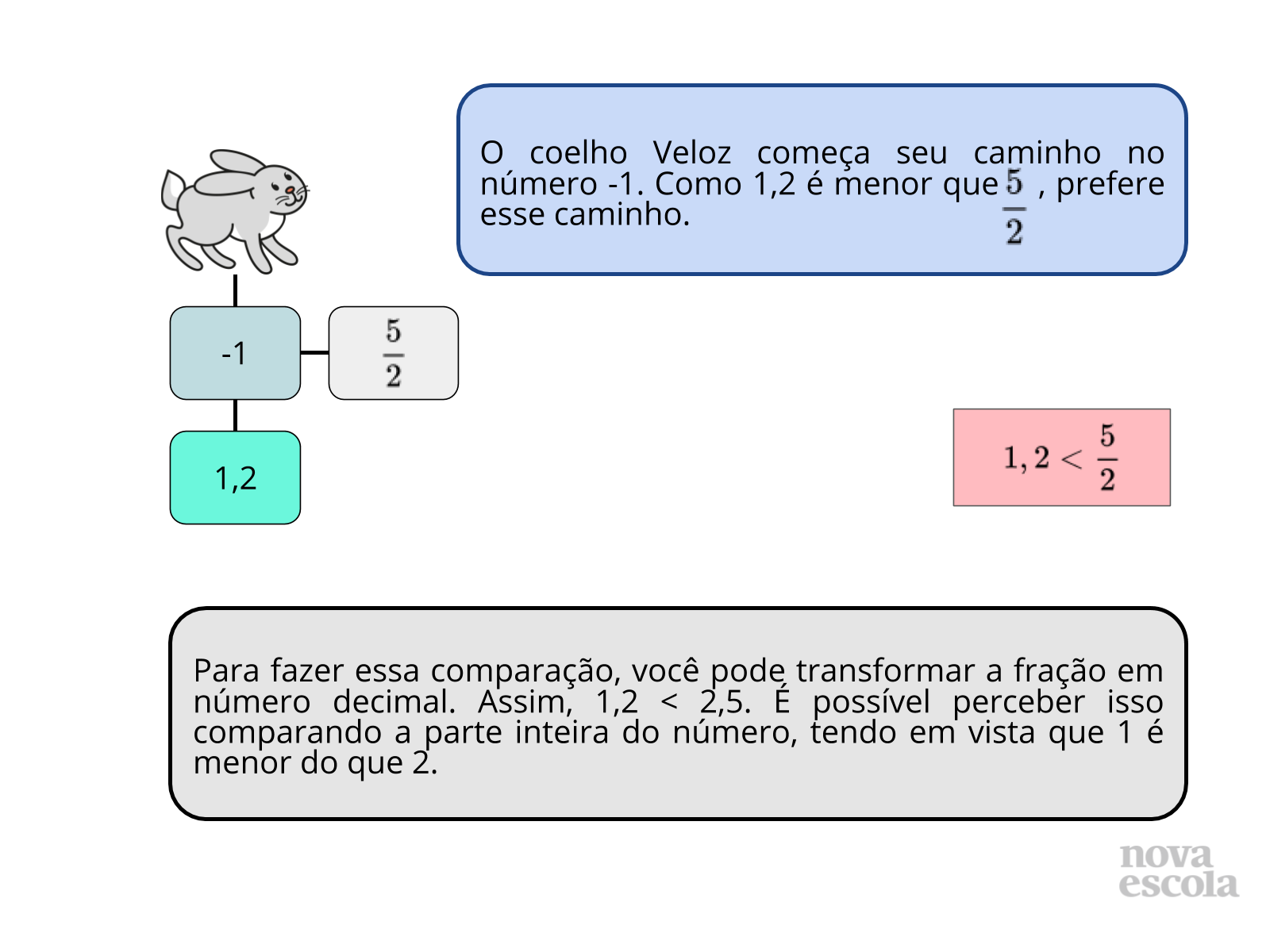
Tempo sugerido: 7 minutos (slides 6 a 14)
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
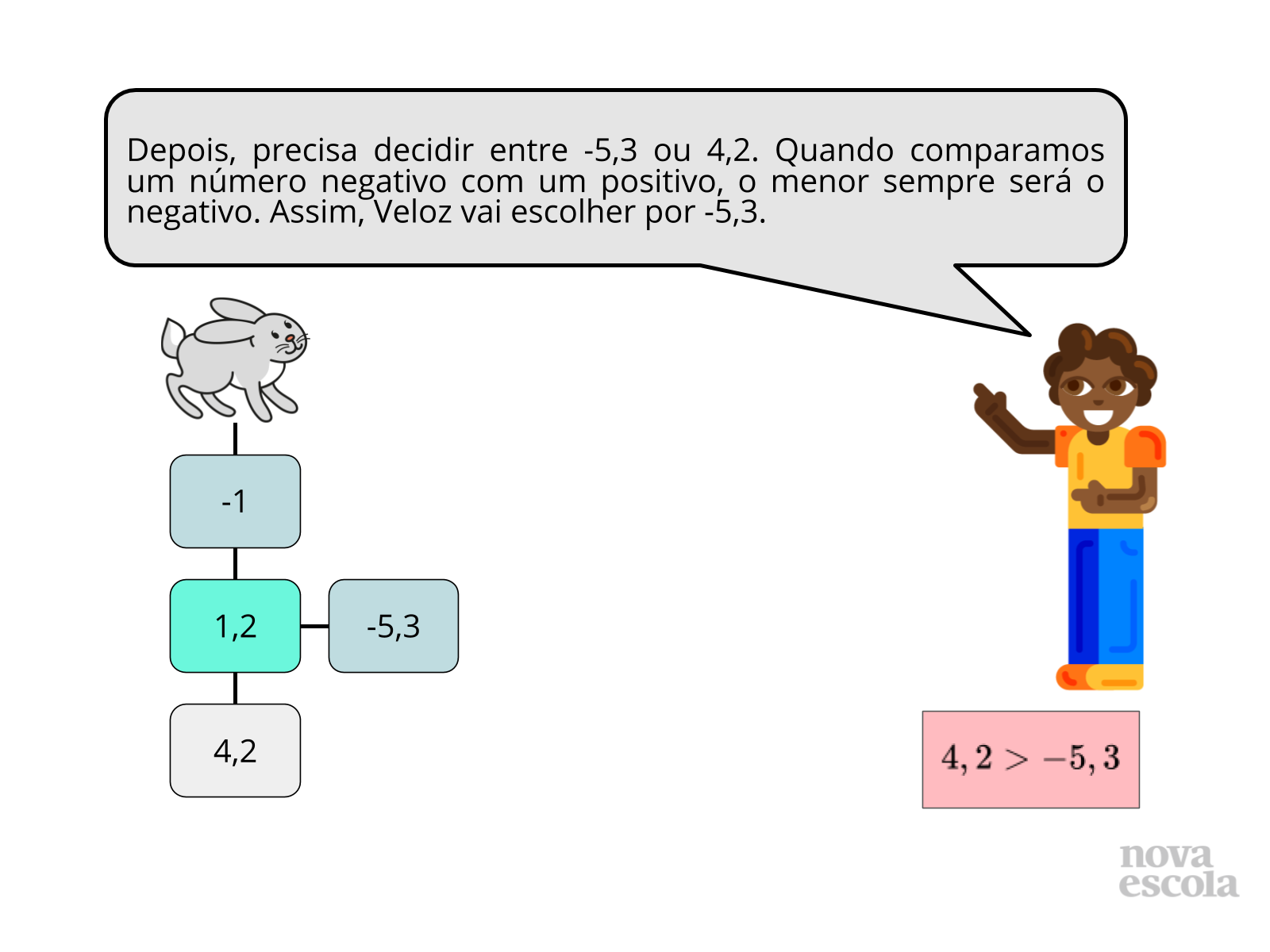
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte I
Tempo sugerido: 7 minutos (slides 6 a 14)
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
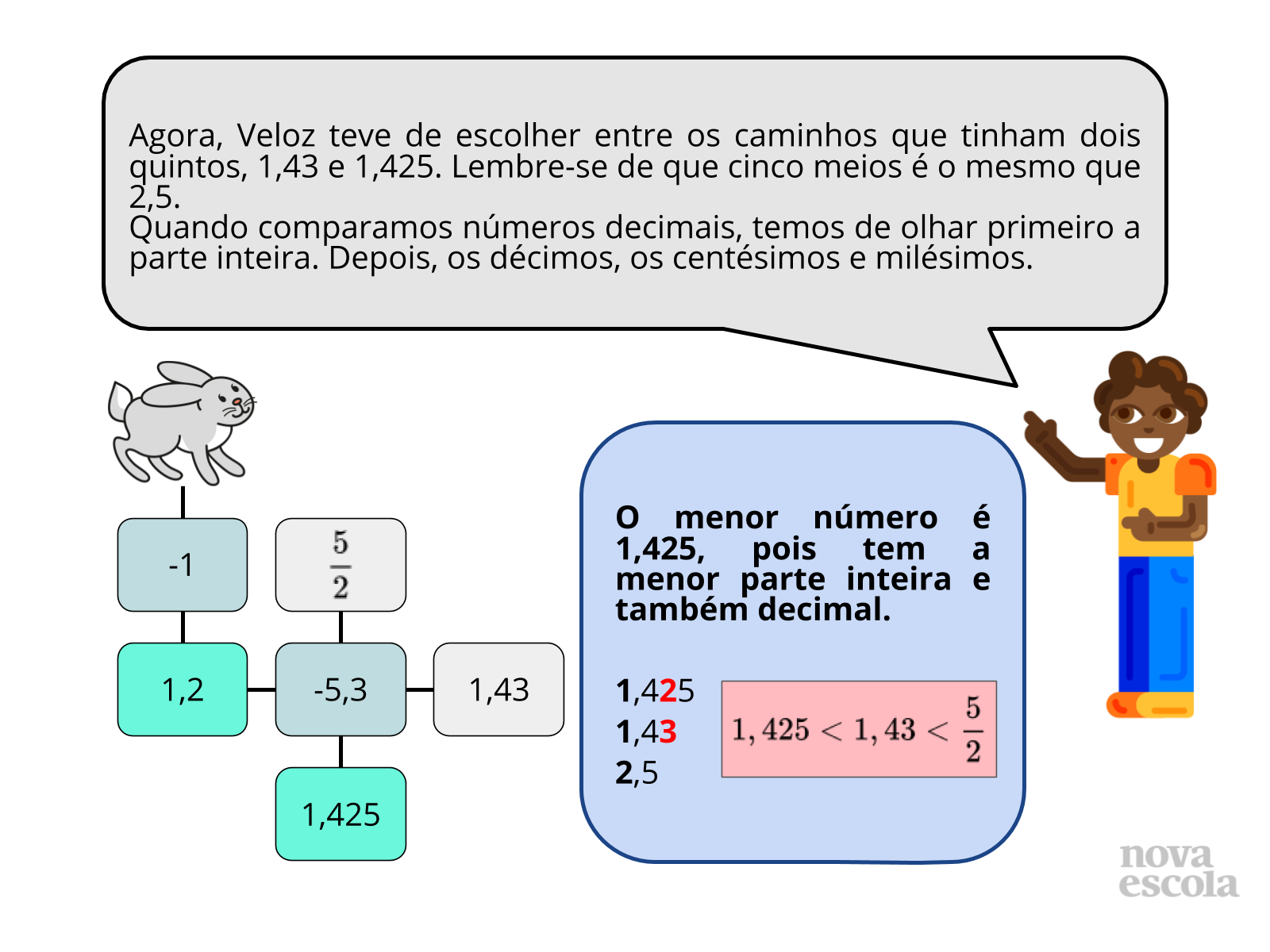
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte I
Tempo sugerido: 7 minutos (slides 6 a 14)
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
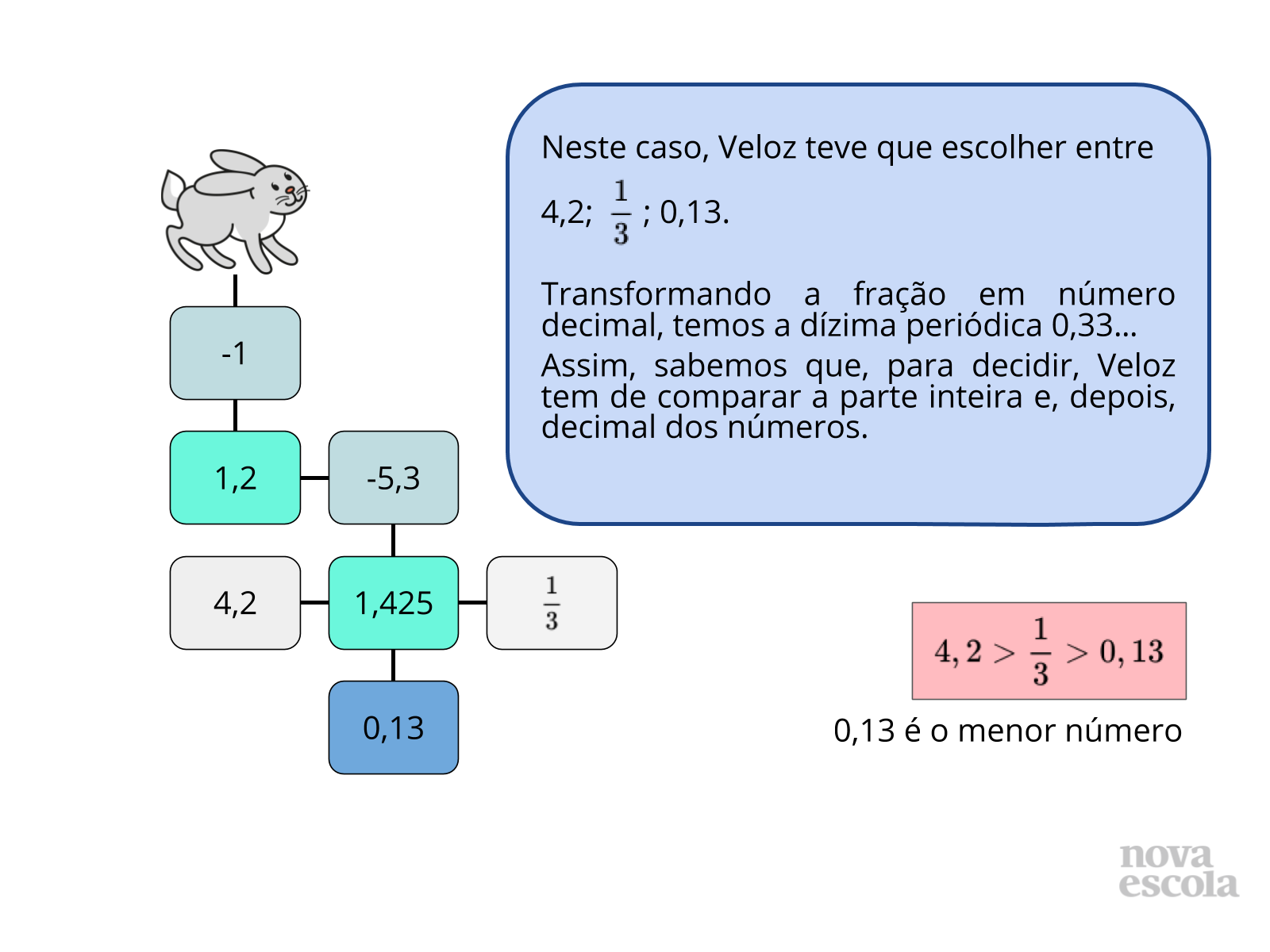
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte I
Tempo sugerido: 7 minutos (slides 6 a 14)
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
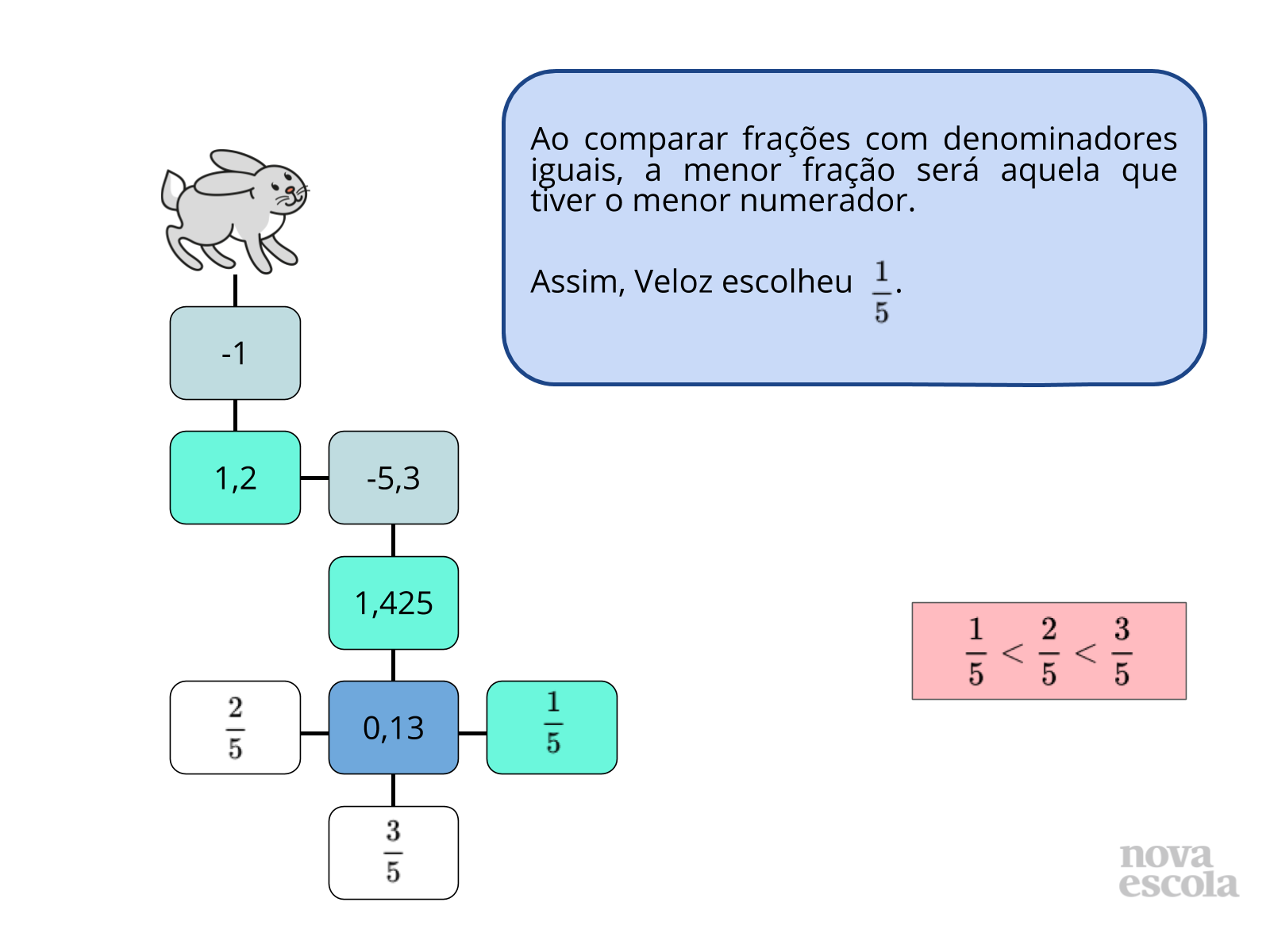
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte I
Tempo sugerido: 7 minutos (slides 6 a 14)
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte I
Tempo sugerido: 7 minutos (slides 6 a 14)
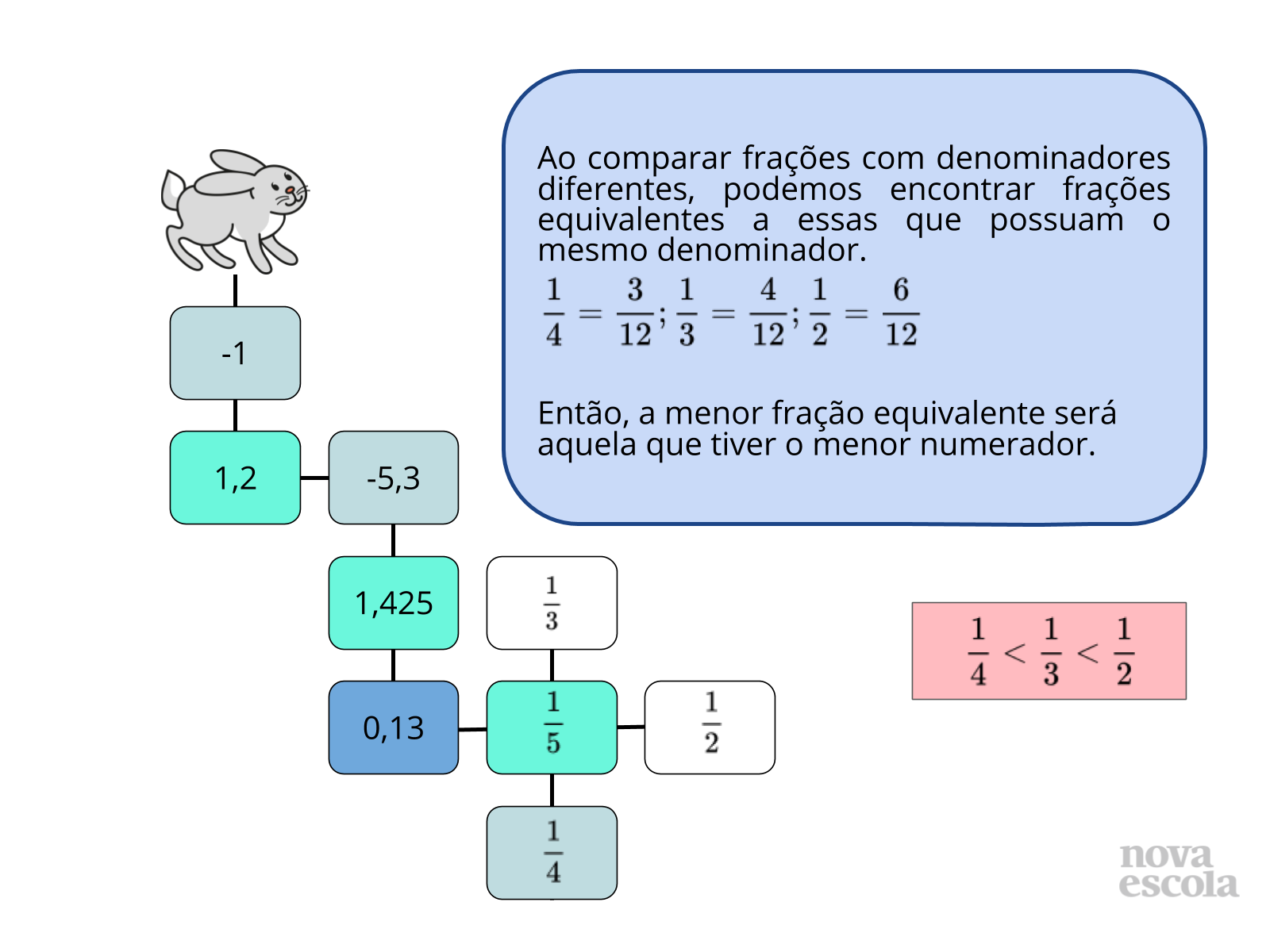
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte I
Tempo sugerido: 7 minutos (slides 6 a 14)
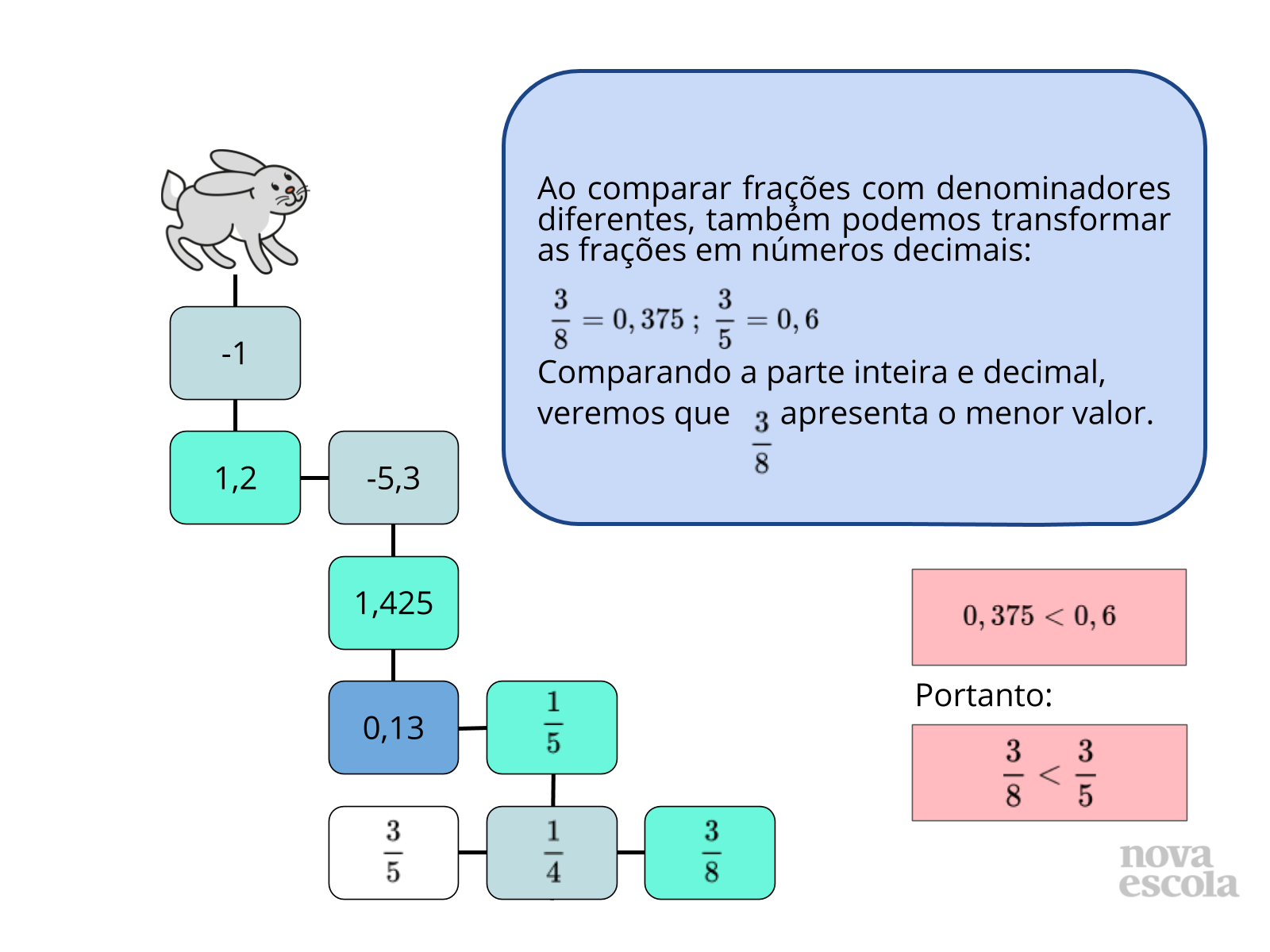
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte I
Tempo sugerido: 7 minutos (slides 6 a 14)
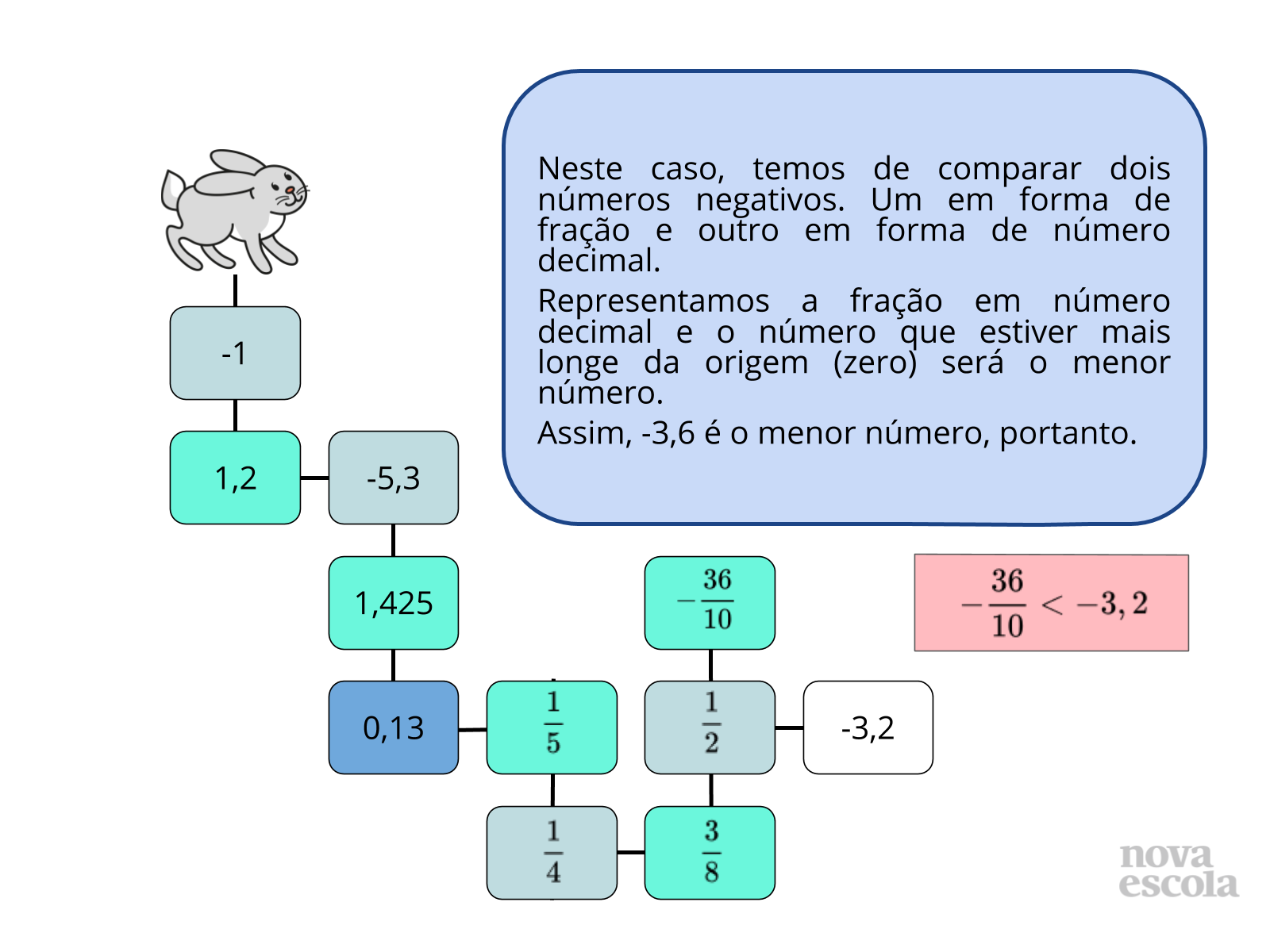
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte I
Tempo sugerido: 7 minutos (slides 6 a 14)
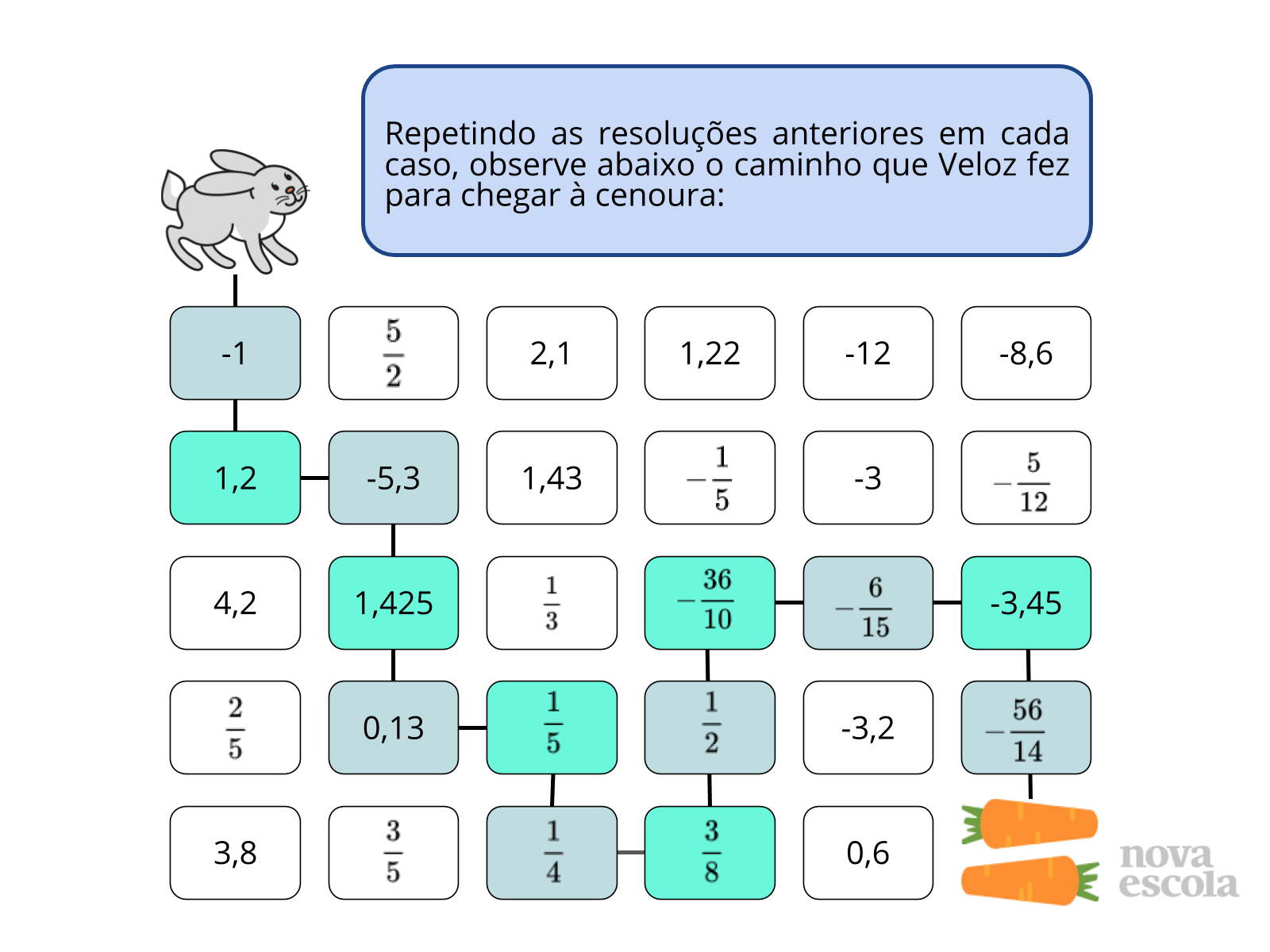
Orientação: Baseado nas observações que você fez durante a atividade, escolha alguns alunos para compartilharem os caminhos escolhidos em cada etapa da atividade. Sempre questione aos alunos o motivo pelo qual escolheram o caminho. Depois das primeiras interações da turma, passe para esta série de slides, como forma explicar cada um dos caminhos. Caso não haja projetor, você pode reproduzir o conteúdo no quadro ou apenas dialogar com os alunos.
Propósito: Fazer com que os alunos compartilhem as soluções de como comparar os números racionais envolvidos.
Discuta com a turma:
- Por que Veloz escolheu ir pelo caminho -5,3 ao invés de 4,2?
- Por que Veloz preferiu o número 1,425 ao invés de 1,43?
- Como podemos entender o porquê de ¼ ser menor do que ½ e ??
- Por qual razão -5/12 é maior -56/14?
Discussão das soluções parte II
Tempo sugerido: 5 minutos
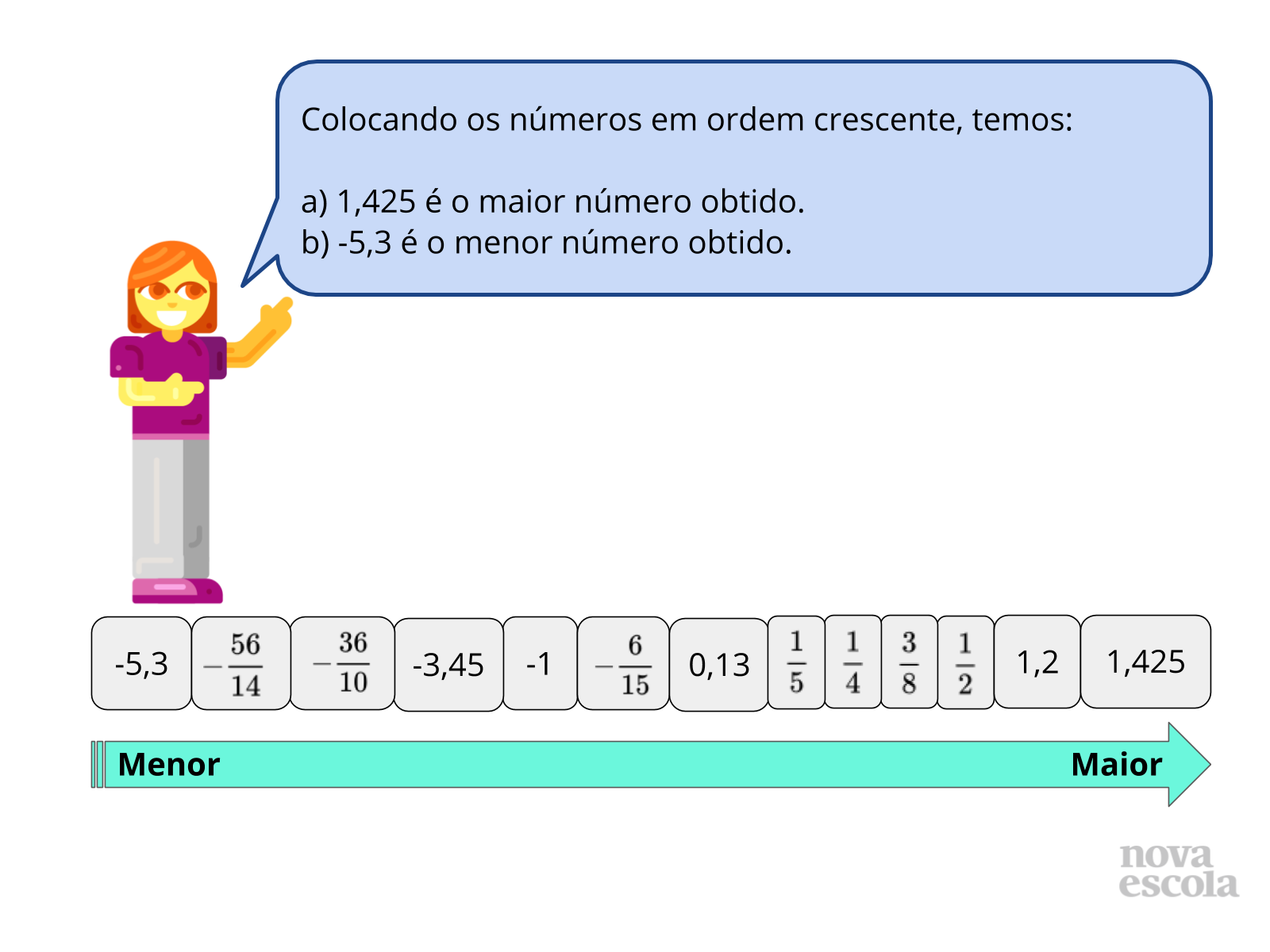
Orientação: Peça para que os alunos compartilhem a ordem crescente dos números. Sempre questione aos alunos o motivo pelo qual escolheram o número, comparando-o ao resto dos números que ainda podem ser escolhidos. Depois das primeiras interações da turma, passe para este slide, como forma de mostrar a resolução correta. Caso não haja projetor, você pode reproduzir o conteúdo.
Propósito: Fazer com que os alunos compartilhem as soluções que deram para a ordenação crescente dos números.
Discuta com a turma:
- Por que 1,425 é o maior número obtido?
- Por que -5,3 é o menor número obtido?
Sistematizando o conceito
Tempo sugerido: 5 minutos (slides 16 e 17).
Orientação: Discuta com a turma sobre como comparar e ordenar números racionais, tendo certeza de que eles consigam ampliar para a comparação de números negativos racionais. O aluno deve ter clareza de que pode transformar a fração em número decimal para realizar a comparação. Também deve ter conhecimento de que, assim como os números inteiros, os números racionais negativos são menores o quão mais distante estiverem da origem (zero).
Propósito: Sistematizar os conceitos da aula, apresentando a forma de comparar números racionais positivos e negativos, bem como ordená-los.
Discuta com a turma:
- Ao comparar números racionais em sua forma positiva, o processo é o mesmo que você já conhecia ou mudou alguma coisa? E na forma negativa?
- Durante a aula, quais erros cometemos ao comparar números racionais? O que esses erros nos ensinaram?
Sistematizando o conceito
Tempo sugerido: 5 minutos (slides 16 e 17).
Orientação: Discuta com a turma sobre como comparar e ordenar números racionais, tendo certeza de que eles consigam ampliar para a comparação de números negativos racionais. O aluno deve ter clareza de que pode transformar a fração em número decimal para realizar a comparação. Também deve ter conhecimento de que, assim como os números inteiros, os números racionais negativos são menores o quão mais distante estiverem da origem (zero).
Propósito: Sistematizar os conceitos da aula, apresentando a forma de comparar números racionais positivos e negativos, bem como ordená-los.
Discuta com a turma:
- Ao comparar números racionais em sua forma positiva, o processo é o mesmo que você já conhecia ou mudou alguma coisa? E na forma negativa?
- Durante a aula, quais erros cometemos ao comparar números racionais? O que esses erros nos ensinaram?
Encerramento
Tempo sugerido: 2 minutos.
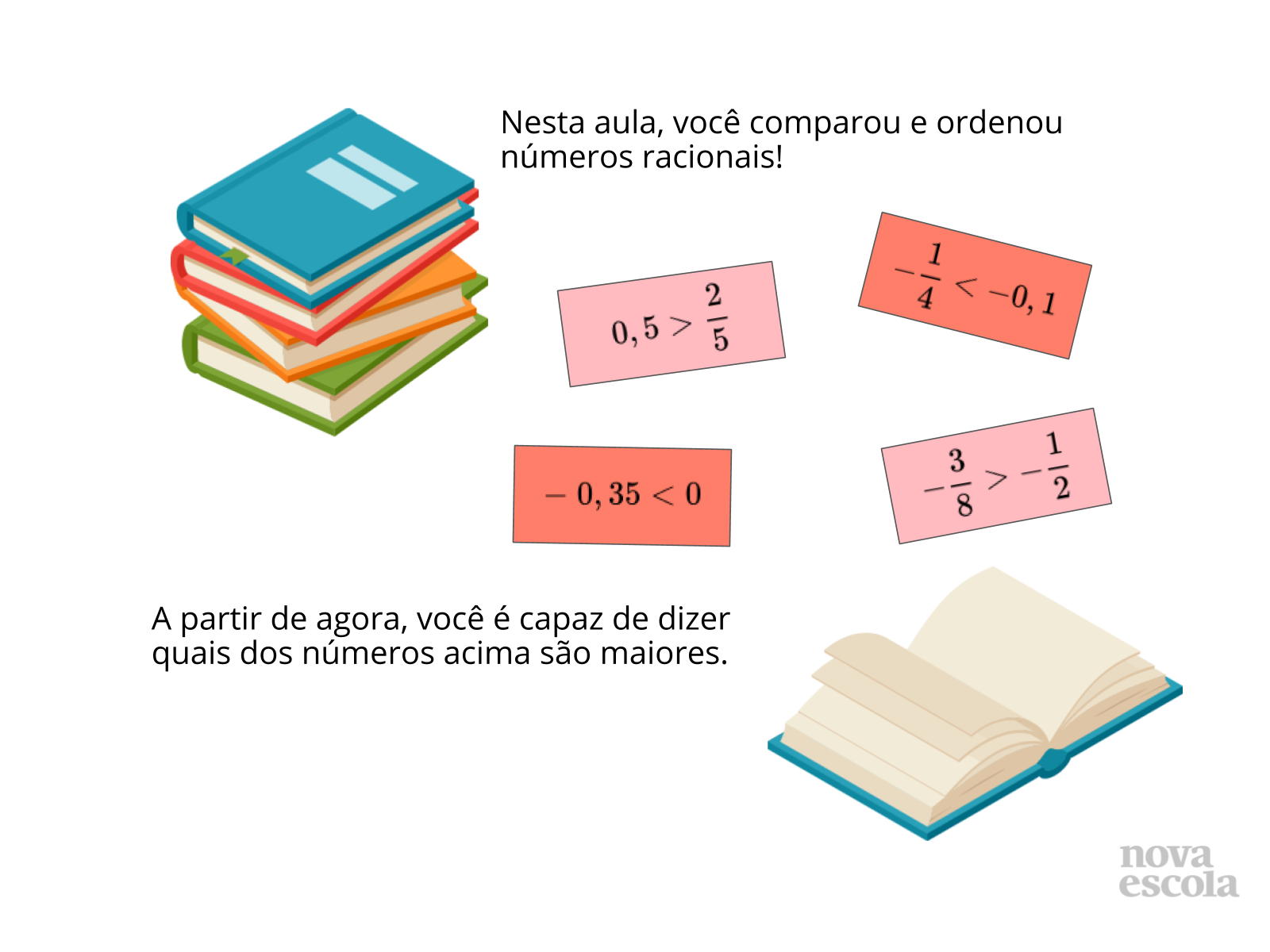
Orientação: Encerre a aula relembrando qual foi a aprendizagem adquirida pelos alunos e escolha 3 alunos que possam opinar sobre os seguintes tópicos:
- Qual parte da aula você mais teve facilidade?
- Qual parte da aula você teve dificuldade, mas vai se esforçar para aprender?
- Qual conteúdo envolvendo números racionais você está ansioso para começar a aprender?
Propósito: Resumir as aprendizagens do dia e refletir sobre a aula.
Raio x
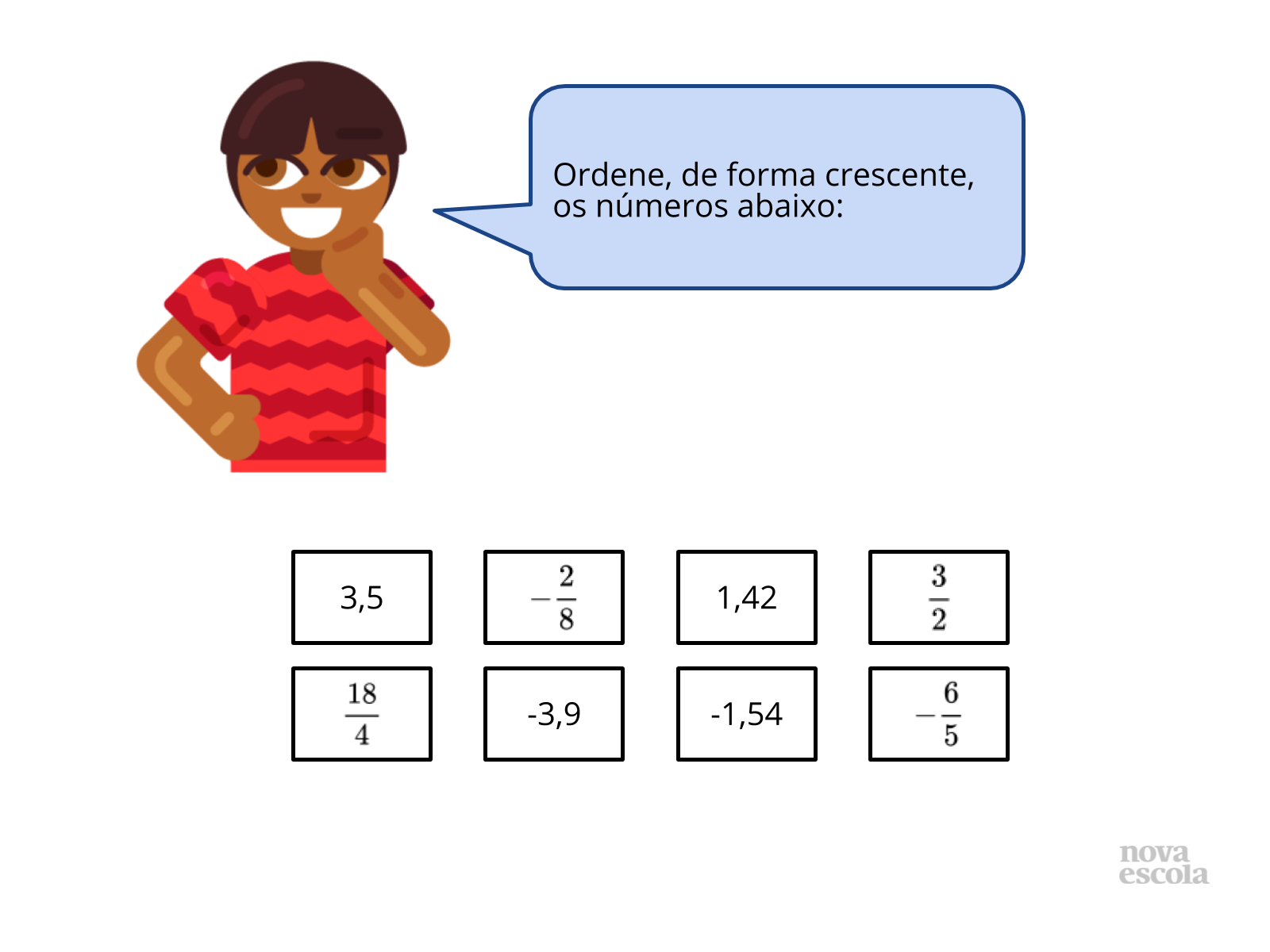
Tempo sugerido: 6 minutos.
Orientações: Separe, para cada aluno, uma folha de papel recortada, onde os alunos terão de colocar o nome e responder a atividade. Você pode projetar, passar no quadro ou fazer cópia da atividade para os alunos. Circule para verificar como os alunos estão ordenando os números. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então recolha as respostas de cada aluno e anote comentários sobre eles. No fim da aula você pode responder a atividade com os alunos e discutir com a turma sobre os conceitos envolvidos.
Você pode fazer o download desta atividade para imprimir para os seus alunos aqui.
Acesse aqui a resolução desta atividade.
Propósito: Avaliar se os alunos conseguem comparar e ordenar números racionais em suas formas diversas.
Discuta com a turma:
- Qual é o menor número apresentado? Qual é o maior?
