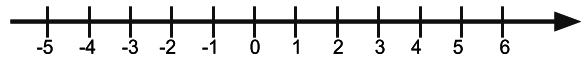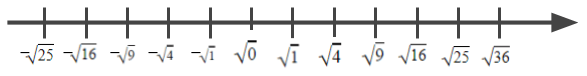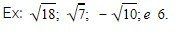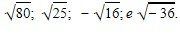Resumo da aula
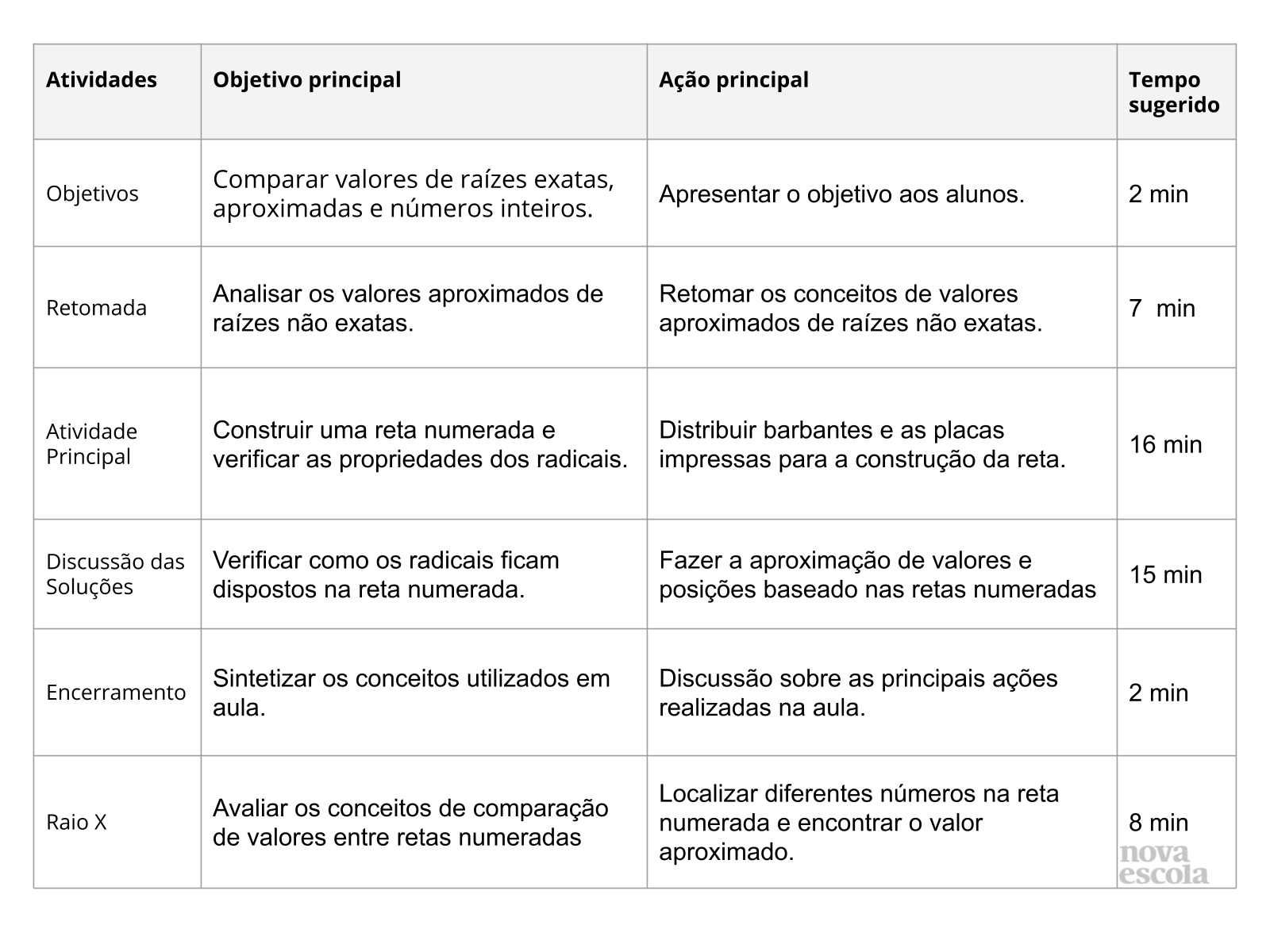
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Propósito: Esclarecer o objetivo aos estudantes.
Orientação: Apresente o objetivo aos alunos.
Discuta com a turma:
Aquecimento
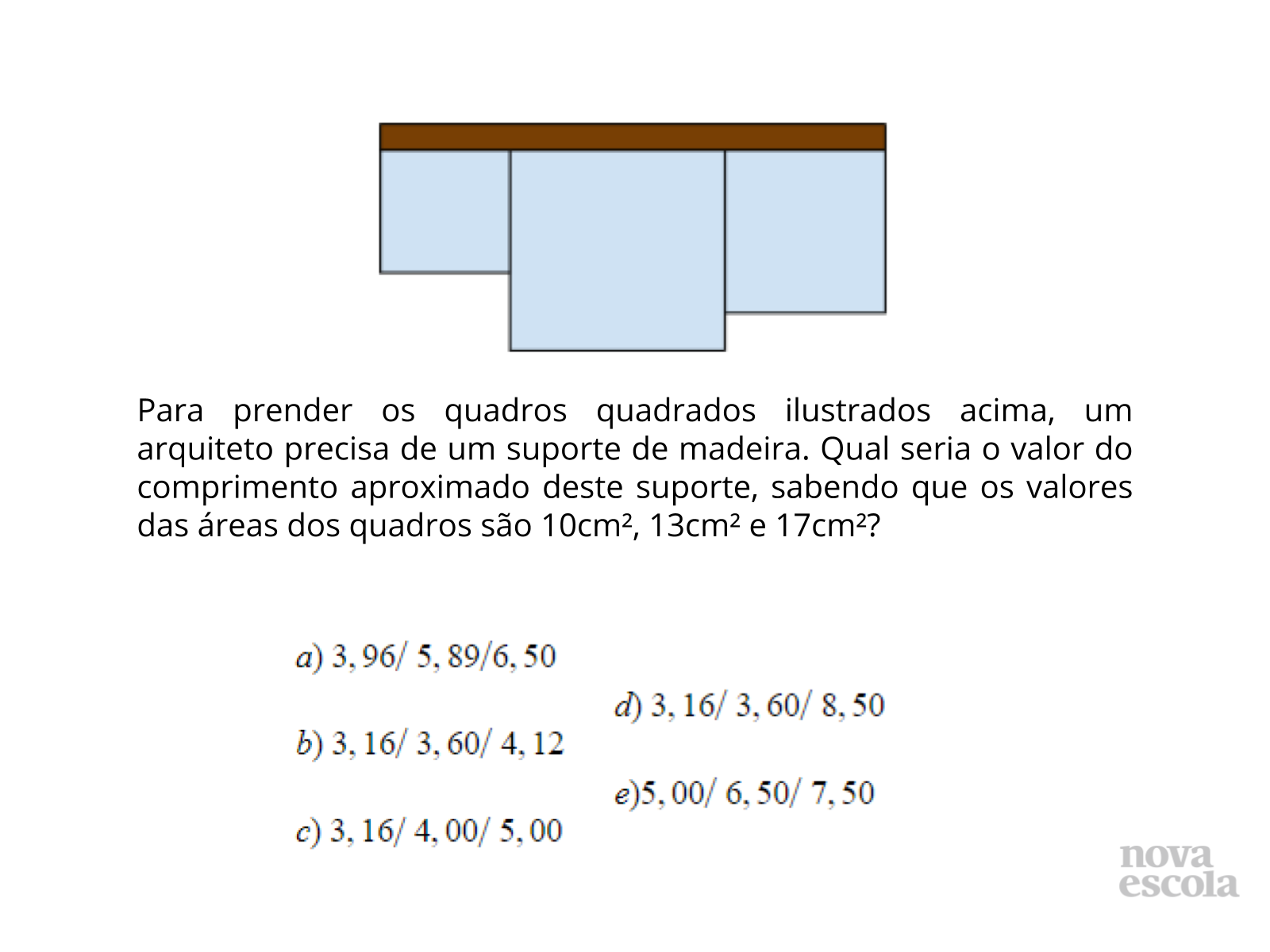
Tempo sugerido: 7 minutos.
Propósito: Analisar os valores aproximados de raízes não exatas.
Orientação: Se tratando de uma revisão, mostre aos alunos a ideia de se resolver através de intervalos de valores.
Discuta com a turma:
- Como encontrar os intervalos usando raízes exatas.
- Quais são as raízes exatas com valor menor ou maior que a raiz desejada.
- Como isso poderia auxiliar para calcular o valor aproximado da raiz?
Materiais complementares para impressão:
Aquecimento
Resolução do aquecimento
Atividade principal

Orientação: Entregue aos alunos dois pedaços de barbante de 2,5 metros cada. Para esta atividade existem duas possibilidades, em grupo de até 4 pessoas ou com o professor comandando na frente da sala. Se decidir por grupos, organize a sala para que os alunos possam fixar os barbantes na parede. Caso decida realizar na frente, fixe os barbantes na lousa. A todo momento peça para os alunos fazerem medições, marcações e estimativas anotando em seus cadernos.
Propósito: Criar um esqueleto da reta numerada.
Discuta com a turma:
- Como podemos associar este bartante a uma reta numerada?
- Existem diferentes formas de representar os números?
- Podemos fazer uma reta numerada com radicais?
Materiais complementares para impressão:
Atividade principal
Resolução da atividade principal
Guia de intervenção
Atividade principal
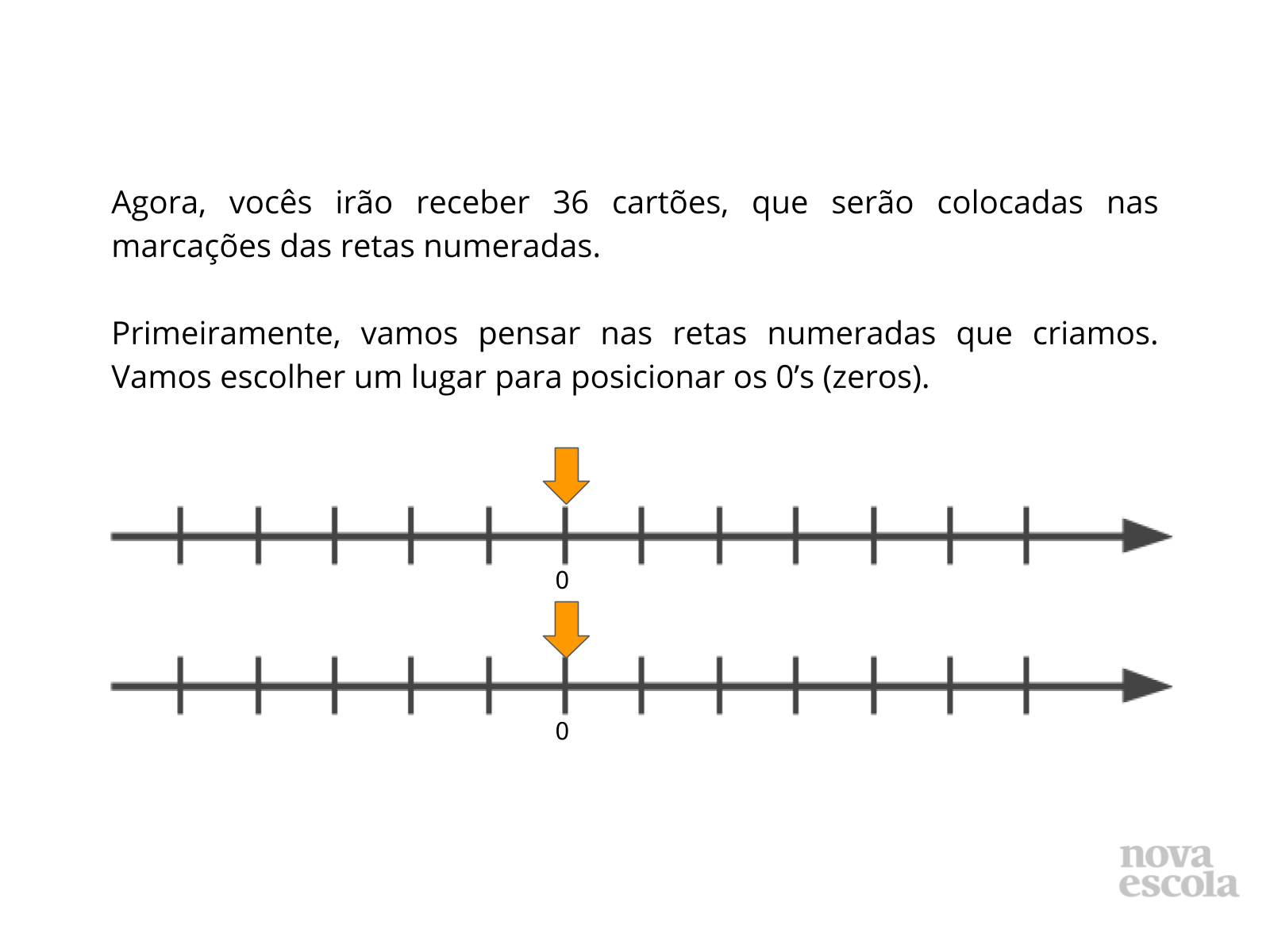
Tempo sugerido: 16 minutos (slides 4 a 8).
Orientação: Primeiro apresente a reta numerada em branco (animação). Espere os alunos pensarem um pouco, e discuta que podemos ter números positivos e negativos. Termine passando a animação. Diga que para esta atividade temos que colocar os zeros na mesma posição. As placas estão em formato de impressão junto à atividade da aula.
Propósito: Iniciar a construção da reta numerada.
Discuta com a turma:
- Como poderão ser organizados os números?
Atividade principal
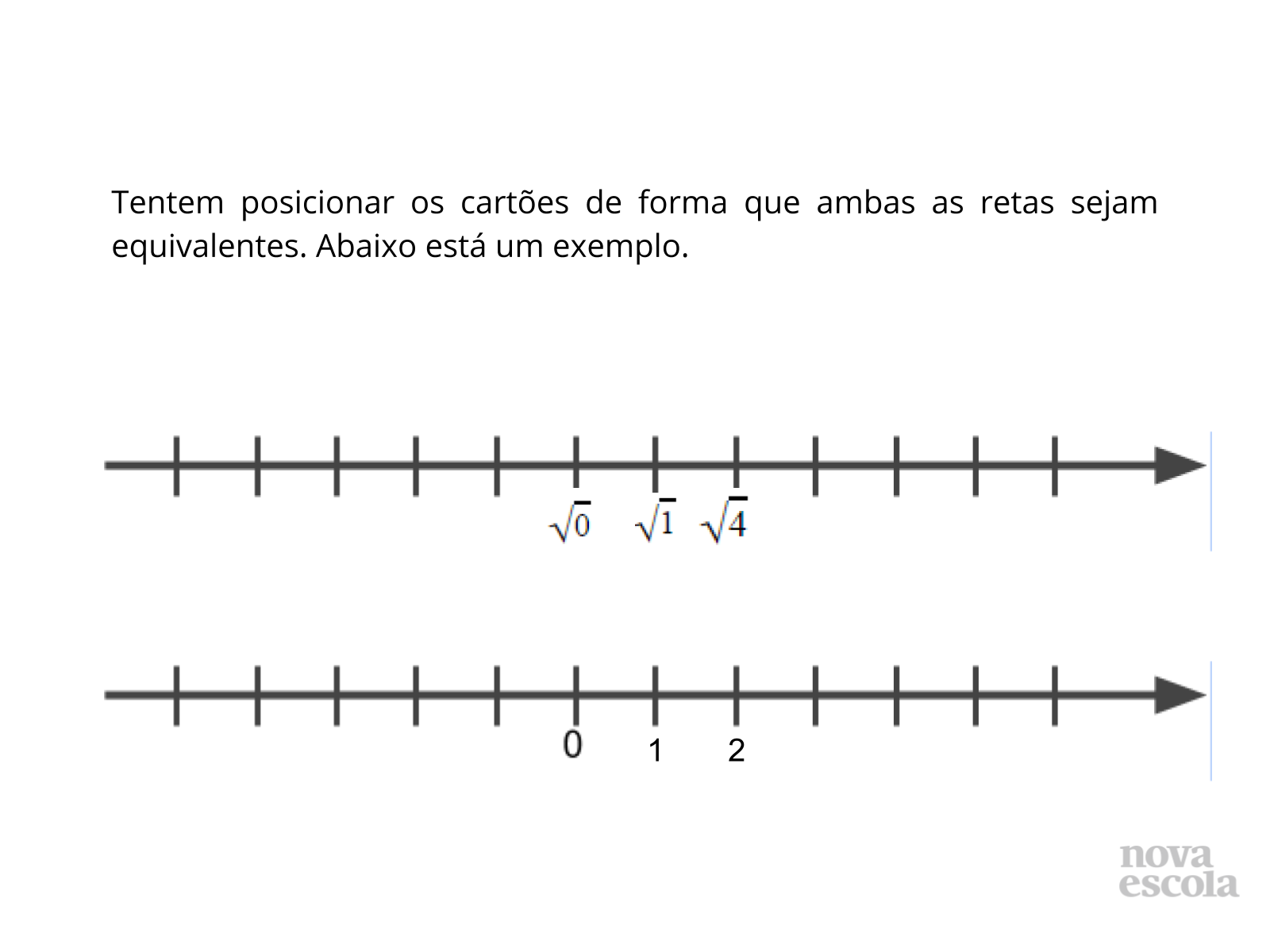
Tempo sugerido: 16 minutos (slides 4 a 8).
Orientação: Peça aos estudantes posicionarem os números dados no exemplo. Em seguida, diga para analisarem as cartões e posicioná-los de forma a completar as retas.
Propósito: Continuar a construção da reta numerada.
Discuta com a turma:
- Qual a relação que pode ser feita com os números e os números na forma de raiz?
- E quando são números negativos?
- Existem números negativos dentro da raíz?
Atividade principal

Tempo sugerido: 16 minutos (slides 4 a 8).
Orientação: Peça anotarem os números do slide em plaquinhas em branco e então diga aos estudantes posicionarem os números dados. Em seguida, diga para analisarem as placas e com base nisso calcular o que se pede.
Propósito: Propor uma atividade baseada na construção da reta numerada.
Discuta com a turma:
- Qual a relação que pode ser feita com os números e os números na forma de raiz?
- E quando são números negativos?
- Existem números negativos dentro da raiz?
- Podemos fazer aproximações utilizando a reta numerada?
Atividade principal

Tempo sugerido: 16 minutos (slides 4 a 8).
Propósito: Perceber as dificuldades dos alunos.
Orientação: Perceba a expressão dos alunos após a atividade.
Discuta com a turma:
- Qual foi o valor mais difícil de encontrar?
Discussão da solução

Tempo sugerido: 15 minutos (slides 9 a 15).
Orientação: A parte mais importante desta análise é o aluno saber localizar a raiz nas retas numeradas, por isso, espere os alunos mostrarem a localização. Para os cálculos utilize a construção no barbante como analogia.
Propósito: Localizar e calcular o valor aproximado do radical indicado no cartão.
Discuta com a turma:
- Qual a relação entre as duas retas numeradas?
Discussão da solução

Tempo sugerido: 15 minutos (slides 9 a 15).
Propósito: Localizar e calcular o valor aproximado de uma raiz negativa.
Orientação: Peça aos alunos se atentarem ao sinal negativo fora da raiz. Questione sobre as possibilidades, e formas que podem ser resolvidas a raiz, sendo a fatoração uma delas.
Discuta com a turma:
- Qual a diferença entre raiz negativa e a raiz de um número negativo?
Discussão da solução

Tempo sugerido: 15 minutos (slides 9 a 15).
Orientação: A parte mais importante desta análise é o aluno saber localizar a raiz nas retas numeradas, por isso, espere os alunos mostrarem a localização. Para os cálculos utilize a construção no barbante como analogia.
Propósito: Localizar e calcular o valor aproximado do radical indicado no cartão.
Discuta com a turma:
- Qual a relação entre as duas retas numeradas?
Discussão da solução

Tempo sugerido: 15 minutos (slides 9 a 15).
Propósito: Verificar um radical aproximado para dado valor numérico.
Orientação: Proceda de maneira parecida aos casos anteriores. Questione aos estudantes qual a relação entre o resultado e o número dentro da raiz (elevado ao quadrado).
Discuta com a turma:
- Qual a relação da potência de 2 (elevar ao quadrado) com a radiciação?
- Como fazer o processo inverso?
Discussão da solução

Tempo sugerido: 15 minutos (slides 9 a 15).
Propósito: Verificar um radical aproximado para dado valor numérico.
Orientação: Proceda de maneira parecida aos casos anteriores. Questione aos estudantes qual a relação entre o resultado e o número dentro da raiz (elevado ao quadrado). Atentar-se que o valor é negativo.
Discuta com a turma:
- Qual a relação da potência de 2 (elevar ao quadrado) com a radiciação?
- Como fazer o processo inverso?
Discussão da solução

Tempo sugerido: 15 minutos (slides 9 a 15).
Propósito: Localizar e calcular o valor aproximado de uma raiz negativa.
Orientação: Peça aos alunos se atentarem ao sinal negativo fora da raiz. Questione sobre as possibilidades, e formas que podem ser resolvidas a raiz, sendo a fatoração uma delas.
Discuta com a turma:
- Qual a diferença entre raiz negativa e a raiz de um número negativo?
Discussão da solução
Tempo sugerido: 15 minutos (slides 9 a 15).
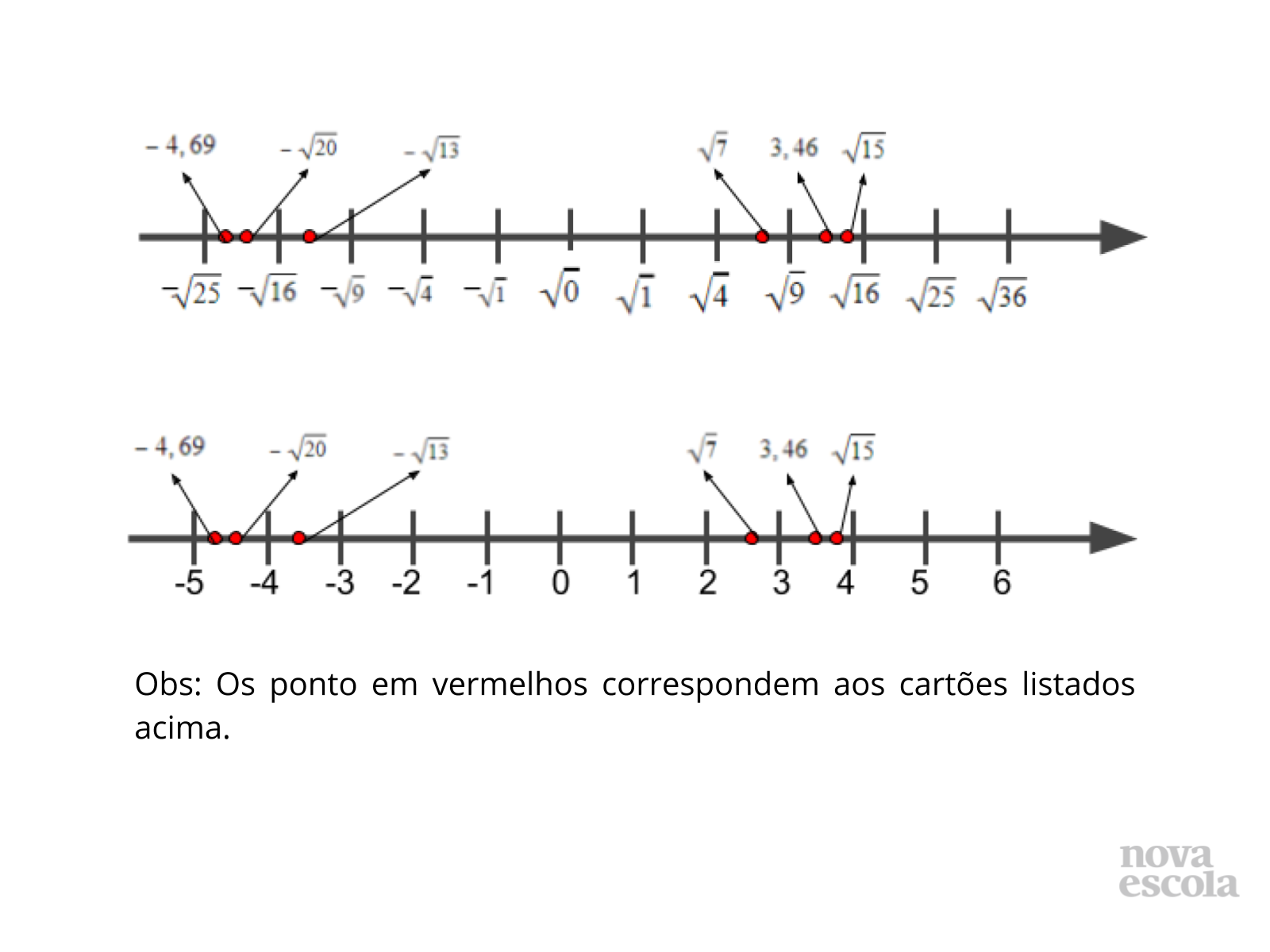
Propósito: Mostrar como estimar valores de soma de radicais através das retas numeradas.
Orientação: Pergunte se os alunos conseguiram estimar alguns valores. Explique as partes e indique na figura onde se localiza o valor dos radicais.
Discuta com a turma:
- Como podemos descobrir o valor de cada raiz?
- Como podemos utilizar os intervalos para nos ajudar?
- Como supomos qual melhor aproximação?
Encerramento
Tempo sugerido: 2 minutos.
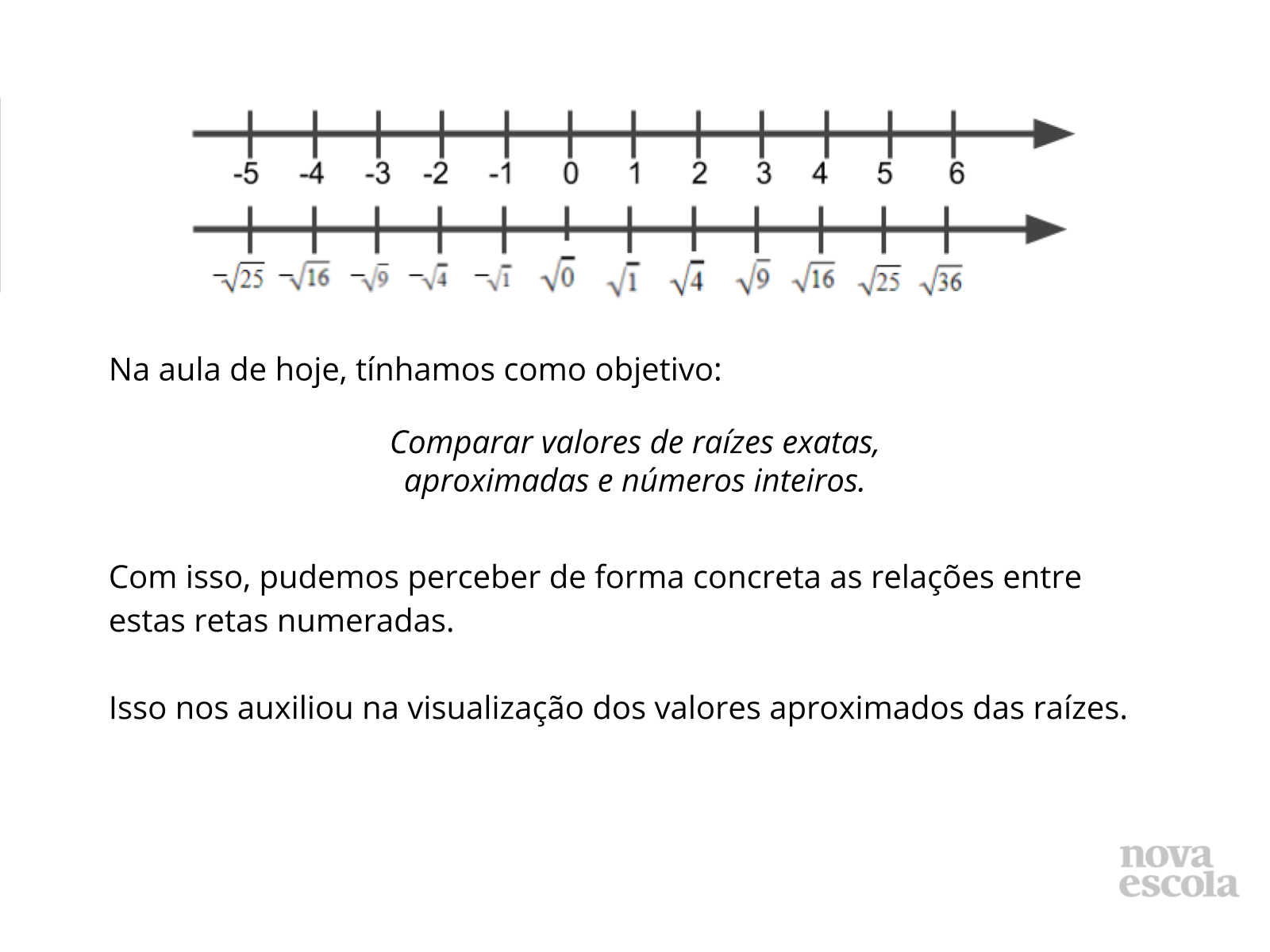
Orientação: Discuta com a sala os principais tópicos, pedindo aos alunos citarem exemplos quando for possível.
Propósito: Finalizar a aula retomando a importância do conceito estudado.
Discuta com a turma:
- Onde poderia ser aplicado a aproximação de raízes não exatas?
Raio X
Tempo sugerido: 5 minutos.
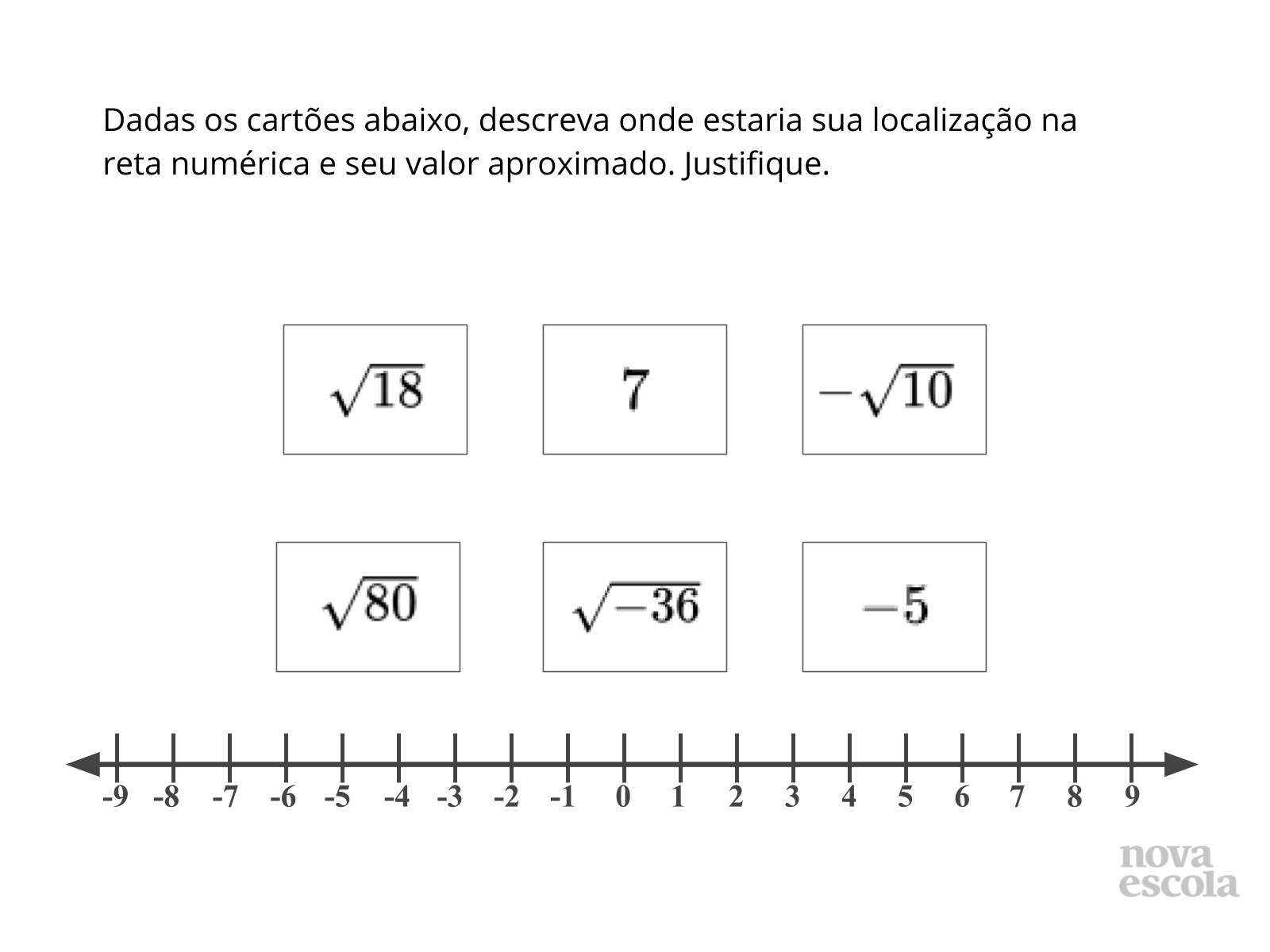
Propósito: Avaliar os conceitos aprendidos em aula.
Orientação: Peça aos alunos criarem uma linha em seus cadernos, marcando um ponto como zero. Em seguida, peça para numerarem. E então, dispor os números acima nesta linha. Repare que a raiz de número negativo não existe nos reais. Peça então para estimarem os valores de cada cartão.
Discuta com a turma:
- Valores aproximados de raízes
- Valores negativos de raízes
- Raízes de valores negativos
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.