Atividade principal
Plano de Aula
Plano de aula: Investigando Propriedades de Quadriláteros: Trapézio e Paralelogramo
Plano 2 de uma sequência de 10 planos. Veja todos os planos sobre Propriedades de quadriláteros
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Geisa Zilli Shinkawa da Silva
Mentor: Fabrício Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
Investigar as propriedades dos paralelogramos, dos trapézios e trapézios isósceles, utilizando congruência de triângulos. Identificar as principais características dos quadriláteros e suas propriedades, além de reconhecer quadrados, retângulos e losangos como paralelogramos.
Conceito-chave
Propriedades de quadriláteros.
Recursos necessários
- Lápis de escrever, lápis de cor, borracha e tesoura;
- Esquadros e régua;
- Folha de papel A4 (para desenho e recorte);
- Atividades impressas (preferencialmente) ou projetadas.
Habilidades BNCC:
Objetivos de aprendizagem
Investigar as propriedades dos paralelogramos, dos trapézios e trapézios isósceles, utilizando congruência de triângulos. Identificar as principais características dos quadriláteros e suas propriedades, além de reconhecer quadrados, retângulos e losangos como paralelogramos.
Resumo da aula
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Leia individualmente, ou com toda a turma, o objetivo da aula.
Propósito: Compartilhar o objetivo da aula com os alunos
Aquecimento

Tempo sugerido: 5 minutos.
Orientações: Inicialmente, por meio de roda de conversa, deixando os estudantes o mais à vontade possível, pergunte aos alunos se eles lembram o que são quadriláteros e peça também para que mencionem algumas de suas características. Caso algum aluno apresente características equivocadas, espere que seus colegas terminem de apresentar suas ideias e ao final pergunte se aquela característica equivocada está correta ou não e como poderia ser corrigida.
Em seguida, peça aos alunos que esbocem em seus cadernos um paralelogramo e um trapézio, e pergunte-os: quais as principais características do paralelogramo? Quais as principais características do trapézio? Após responderem, pergunte: E se o trapézio for isósceles, quais as suas características? O que o diferencia dos outros trapézios?
Após responderem, anote no quadro algumas das respostas dadas por eles, de modo que você retomá-las ao final da aula, para refutá-las ou validá-las.
Propósito: Fazer com que os alunos relembrem algumas características dos paralelogramos, trapézios e trapézios isósceles.
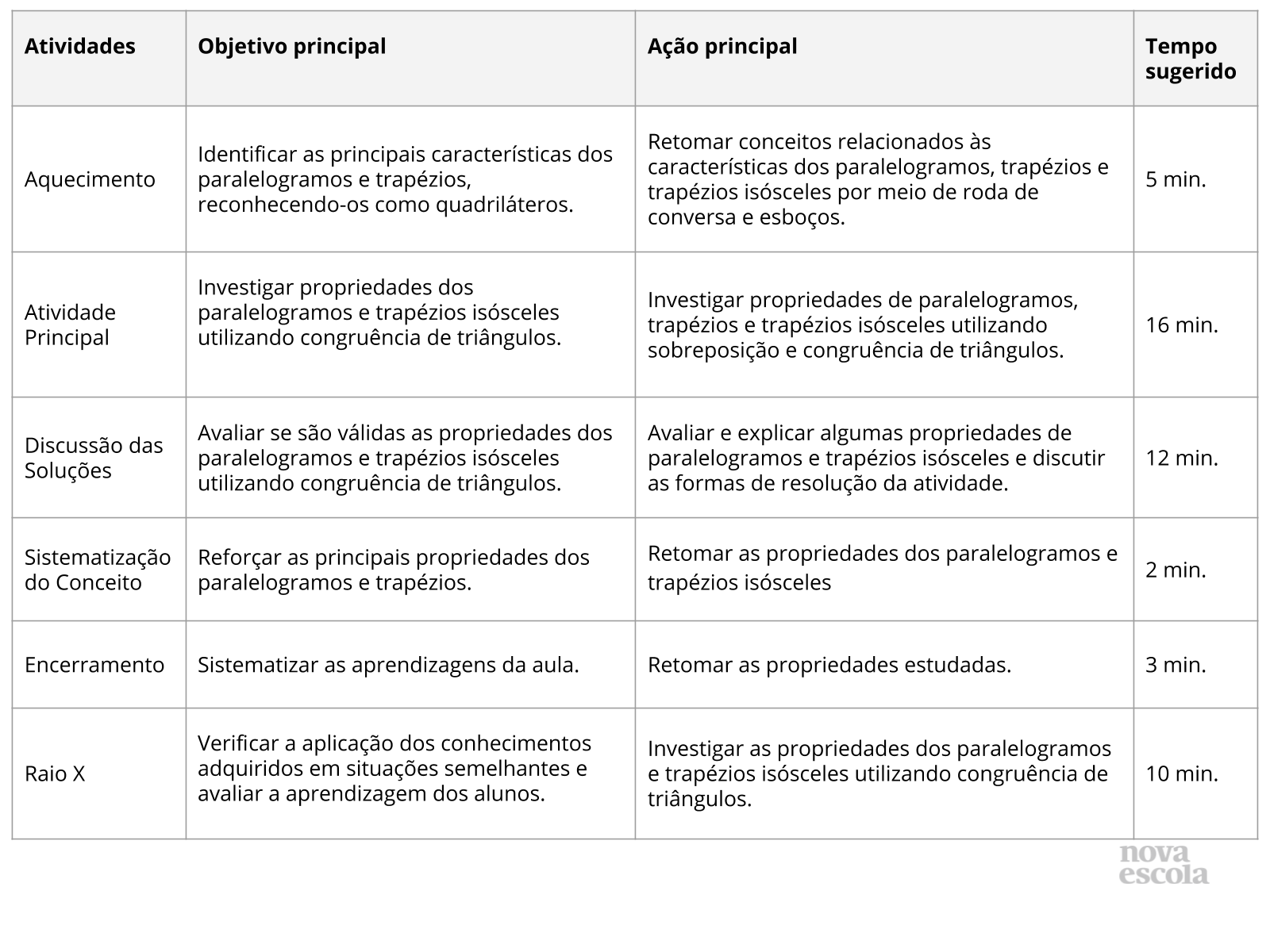
Atividade Principal

Tempo sugerido: 16 minutos. (Slide 4 a 7).
Orientações: Para os slides 4 e 5 projete ou imprima a atividade. Faça uma leitura compartilhada ou individual do enunciado. Peça em seguida que os alunos realizem a atividade individualmente e, logo depois, discutam entre si as soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las.
Se necessário, relembre junto aos alunos o que são quadriláteros, quais são eles e as principais características de cada um. Aos alunos que apresentarem dificuldades, oriente para que eles confeccionem quadriláteros e realizem medições ou dobraduras verificando as propriedades.
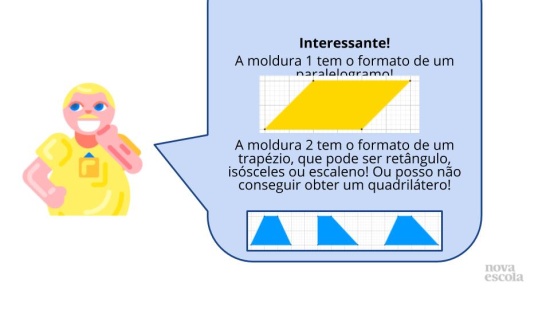
Para os slides 6 e 7, imprima os trapézios disponíveis (duas unidades idênticas) nos materiais complementares, para que o estudante possa manipulá-los, dobrá-los ou recortá-los. Continue a atividade fazendo com os alunos uma leitura compartilhada ou individual do enunciado. Peça aos alunos que realizem a atividade individualmente e, em seguida, discutam com um colega suas soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las.
Se necessário, relembre os casos de congruência de triângulos. Sugira que os estudantes utilizem as imagens dos triângulos e lápis de cor para indicar lados e ângulos com mesma medida, isto é, lados e ângulos congruentes. Peça também que analisem as afirmações de posse dos triângulos, comparando as medidas.
Propósito: Investigar, utilizando a congruência de triângulos, as propriedades dos paralelogramos e trapézios e também aproximar os estudantes das demonstrações formais das propriedades.
Discuta com a turma:
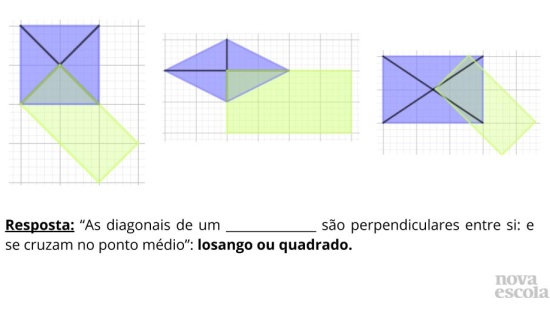
- As diagonais do quadrado se cruzam no ponto médio?
- Existe mais algum quadrilátero em que as diagonais se cruzam no ponto médio? Qual (is)?
- O quadrado é um paralelogramo? O retângulo é um paralelogramo? O losango é um paralelogramo?
- Quais afirmações estão corretas? Como chegou a esta conclusão?
- Quais os casos de congruência de triângulos? E qual o utilizado nesta atividade?
- Qual a propriedade verificada para o trapézio isósceles?
Materiais complementares para impressão:
Atividade Principal

Tempo sugerido: 16 minutos. (Slide 4 a 7).
Orientações: Para os slides 4 e 5, projete ou imprima a atividade. Faça uma leitura compartilhada ou individual do enunciado. Peça em seguida que os alunos realizem a atividade individualmente e, logo depois, discutam entre si as soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las.
Se necessário, relembre junto aos alunos o que são quadriláteros, quais são eles e as principais características de cada um. Aos alunos que apresentarem dificuldades, oriente para que eles confeccionem quadriláteros e realizem medições ou dobraduras verificando as propriedades.
Para os slides 6 e 7, imprima os trapézios disponíveis (duas unidades idênticas) nos materiais complementares, para que o estudante possa manipulá-los, dobrá-los ou recortá-los. Continue a atividade fazendo com os alunos uma leitura compartilhada ou individual do enunciado. Peça aos alunos que realizem a atividade individualmente e, em seguida, discutam com um colega suas soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las.
Se necessário, relembre os casos de congruência de triângulos. Sugira que os estudantes utilizem as imagens dos triângulos e lápis de cor para indicar lados e ângulos com mesma medida, isto é, lados e ângulos congruentes. Peça também que analisem as afirmações de posse dos triângulos, comparando as medidas.
Propósito: Investigar, utilizando a congruência de triângulos, as propriedades dos paralelogramos e trapézios e também aproximar os estudantes das demonstrações formais das propriedades.
Discuta com a Turma:
- As diagonais do quadrado se cruzam no ponto médio?
- Existe mais algum quadrilátero em que as diagonais se cruzam no ponto médio? Qual (is)?
- O quadrado é um paralelogramo? O retângulo é um paralelogramo? O losango é um paralelogramo?
- Quais afirmações estão corretas? Como chegou a esta conclusão?
- Quais os casos de congruência de triângulos? E qual o utilizado nesta atividade?
- Qual a propriedade verificada para o trapézio isósceles?
Atividade Principal
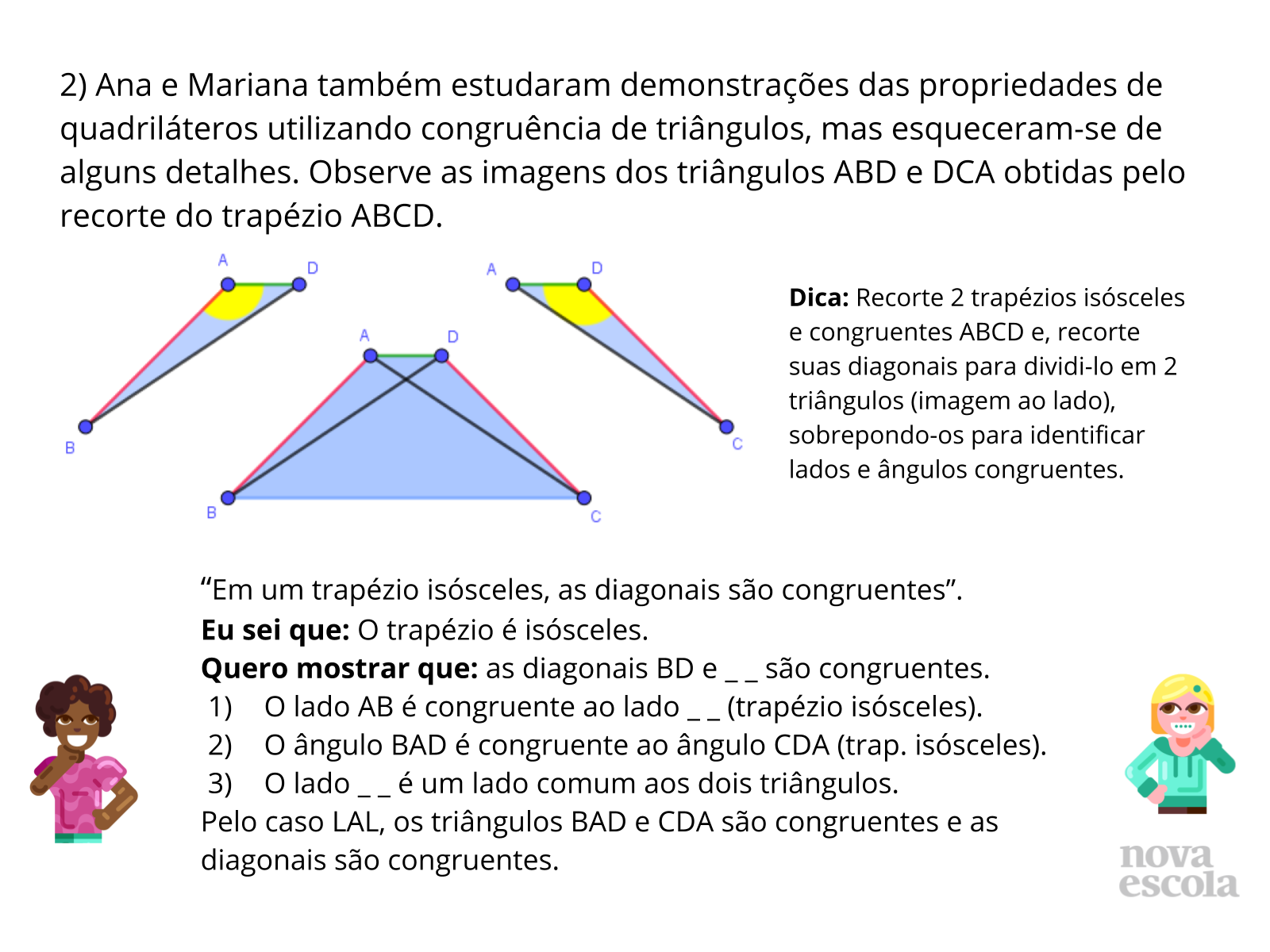
Tempo sugerido: 18 minutos. (Slide 4 a 7).
Orientações: Para os slides 4 e 5 projete ou imprima a atividade. Faça uma leitura compartilhada ou individual do enunciado. Peça em seguida que os alunos realizem a atividade individualmente e, logo depois, discutam entre si as soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las.
Se necessário, relembre junto aos alunos o que são quadriláteros, quais são eles e as principais características de cada um. Aos alunos que apresentarem dificuldades, oriente para que eles confeccionem quadriláteros e realizem medições ou dobraduras verificando as propriedades.
Para os slides 6 e 7, imprima os trapézios disponíveis (duas unidades idênticas) nos materiais complementares, para que o estudante possa manipulá-los, dobrá-los ou recortá-los. Continue a atividade fazendo com os alunos uma leitura compartilhada ou individual do enunciado. Peça aos alunos que realizem a atividade individualmente e, em seguida, discutam com um colega suas soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las.
Se necessário, relembre os casos de congruência de triângulos. Sugira que os estudantes utilizem as imagens dos triângulos e lápis de cor para indicar lados e ângulos com mesma medida, isto é, lados e ângulos congruentes. Peça também que analisem as afirmações de posse dos triângulos, comparando as medidas.
Propósito: Investigar, utilizando a congruência de triângulos, as propriedades dos paralelogramos e trapézios e também aproximar os estudantes das demonstrações formais das propriedades.
Discuta com a Turma:
- As diagonais do quadrado se cruzam no ponto médio?
- Existe mais algum quadrilátero em que as diagonais se cruzam no ponto médio? Qual (is)?
- O quadrado é um paralelogramo? O retângulo é um paralelogramo? O losango é um paralelogramo?
- Quais afirmações estão corretas? Como chegou a esta conclusão?
- Quais os casos de congruência de triângulos? E qual o utilizado nesta atividade?
- Qual a propriedade verificada para o trapézio isósceles?
Atividade Principal

Tempo sugerido: 16 minutos. (Slide 4 a 7).
Orientações: Para os slides 4 e 5 projete ou imprima a atividade. Faça uma leitura compartilhada ou individual do enunciado. Peça em seguida que os alunos realizem a atividade individualmente e, logo depois, discutam entre si as soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las.
Se necessário, relembre junto aos alunos o que são quadriláteros, quais são eles e as principais características de cada um. Aos alunos que apresentarem dificuldades, oriente para que eles confeccionem quadriláteros e realizem medições ou dobraduras verificando as propriedades.
Para os slides 6 e 7, imprima os trapézios disponíveis (duas unidades idênticas) nos materiais complementares, para que o estudante possa manipulá-los, dobrá-los ou recortá-los. Continue a atividade fazendo com os alunos uma leitura compartilhada ou individual do enunciado. Peça aos alunos que realizem a atividade individualmente e, em seguida, discutam com um colega suas soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las.
Se necessário, relembre os casos de congruência de triângulos. Sugira que os estudantes utilizem as imagens dos triângulos e lápis de cor para indicar lados e ângulos com mesma medida, isto é, lados e ângulos congruentes. Peça também que analisem as afirmações de posse dos triângulos, comparando as medidas.
Propósito: Investigar, utilizando a congruência de triângulos, as propriedades dos paralelogramos e trapézios e também aproximar os estudantes das demonstrações formais das propriedades.
Discuta com a turma:
- As diagonais do quadrado se cruzam no ponto médio?
- Existe mais algum quadrilátero em que as diagonais se cruzam no ponto médio? Qual (is)?
- O quadrado é um paralelogramo? O retângulo é um paralelogramo? O losango é um paralelogramo?
- Quais afirmações estão corretas? Como chegou a esta conclusão?
- Quais os casos de congruência de triângulos? E qual o utilizado nesta atividade?
- Qual a propriedade verificada para o trapézio isósceles?
Discussão das Soluções

Tempo sugerido: 12 minutos. (Slides 8 a 13)
Orientações: No slides 8, apresente aos alunos as resoluções da atividade 1, questionando quem respondeu da mesma maneira apresentada. Caso algum aluno tenha respondido de maneira diferente ou traga diferentes argumentos, peça para que compartilhe em voz alta com seus colegas, para que todos possam juntos verificar a validade dos argumentos.
No slide 9, há a continuação das respostas, pergunte também se alguém respondeu de maneira semelhante ou diferentes ao que está nos slides e discuta com eles se es estratégias foram válidas ou não. No final do slide 9, ressalte o item “Relembrando”, e assegure-se que todos os alunos compreenderam a ideia.
Nos slides 9 a 12, apresente cada resposta aos alunos, perguntando sempre se eles responderam de maneira semelhante e pedindo também que alguns deles compartilhem suas resoluções. Aproveite que eles estarão com os triângulos em mãos para solicitar que eles mostrem neles as diagonais, lados congruentes e lados comuns.
Não esqueça de chamar a atenção dos estudantes para as nomenclaturas e definições formais.
Propósito: Compartilhar as resoluções da atividade e também avaliar e explicar algumas propriedades de paralelogramos e trapézios isósceles.
Discuta com a Turma:
- Alguém pensou de forma diferente e chegou à mesma solução? Quais?
- Alguém pensou em outras possibilidades de solução? Quais? Por quê?
Discussão das Soluções

Tempo sugerido: 12 minutos. (Slides 8 a 13)
Orientações: No slides 8, apresente aos alunos as resoluções da atividade 1, questionando quem respondeu da mesma maneira apresentada. Caso algum aluno tenha respondido de maneira diferente ou traga diferentes argumentos, peça para que compartilhe em voz alta com seus colegas, para que todos possam juntos verificar a validade dos argumentos.
No slide 9, há a continuação das respostas, pergunte também se alguém respondeu de maneira semelhante ou diferentes ao que está nos slides e discuta com eles se es estratégias foram válidas ou não. No final do slide 9, ressalte o item “Relembrando”, e assegure-se que todos os alunos compreenderam a ideia.
Nos slides 9 a 12, apresente cada resposta aos alunos, perguntando sempre se eles responderam de maneira semelhante e pedindo também que alguns deles compartilhem suas resoluções. Aproveite que eles estarão com os triângulos em mãos para solicitar que eles mostrem neles as diagonais, lados congruentes e lados comuns.
Não esqueça de chamar a atenção dos estudantes para as nomenclaturas e definições formais.
Propósito: Compartilhar as resoluções da atividade e também avaliar e explicar algumas propriedades de paralelogramos e trapézios isósceles.
Discuta com a turma:
- Alguém pensou de forma diferente e chegou à mesma solução? Quais?
- Alguém pensou em outras possibilidades de solução? Quais? Por quê?
Discussão das Soluções
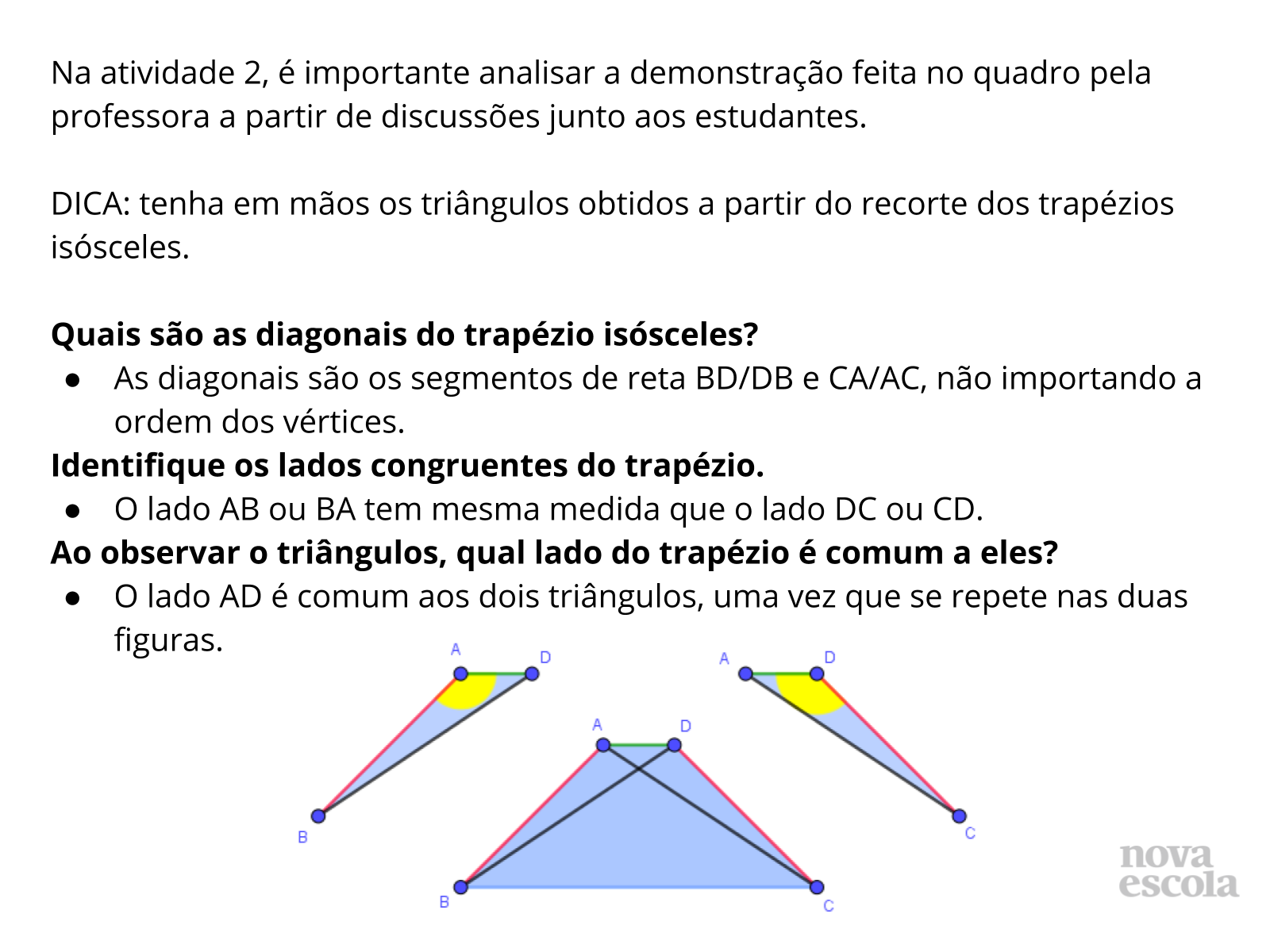
Tempo sugerido: 12 minutos. (Slides 8 a 13)
Orientações: No slides 8, apresente aos alunos as resoluções da atividade 1, questionando quem respondeu da mesma maneira apresentada. Caso algum aluno tenha respondido de maneira diferente ou traga diferentes argumentos, peça para que compartilhe em voz alta com seus colegas, para que todos possam juntos verificar a validade dos argumentos.
No slide 9, há a continuação das respostas, pergunte também se alguém respondeu de maneira semelhante ou diferentes ao que está nos slides e discuta com eles se es estratégias foram válidas ou não. No final do slide 9, ressalte o item “Relembrando”, e assegure-se que todos os alunos compreenderam a ideia.
Nos slides 9 a 12, apresente cada resposta aos alunos, perguntando sempre se eles responderam de maneira semelhante e pedindo também que alguns deles compartilhem suas resoluções. Aproveite que eles estarão com os triângulos em mãos para solicitar que eles mostrem neles as diagonais, lados congruentes e lados comuns.
Não esqueça de chamar a atenção dos estudantes para as nomenclaturas e definições formais.
Propósito: Compartilhar as resoluções da atividade e também avaliar e explicar algumas propriedades de paralelogramos e trapézios isósceles.
Discuta com a turma:
- Alguém pensou de forma diferente e chegou à mesma solução? Quais?
- Alguém pensou em outras possibilidades de solução? Quais? Por quê?
Discussão das Soluções

Tempo sugerido: 12 minutos. (Slides 8 a 13)
Orientações: No slides 8, apresente aos alunos as resoluções da atividade 1, questionando quem respondeu da mesma maneira apresentada. Caso algum aluno tenha respondido de maneira diferente ou traga diferentes argumentos, peça para que compartilhe em voz alta com seus colegas, para que todos possam juntos verificar a validade dos argumentos.
No slide 9, há a continuação das respostas, pergunte também se alguém respondeu de maneira semelhante ou diferentes ao que está nos slides e discuta com eles se es estratégias foram válidas ou não. No final do slide 9, ressalte o item “Relembrando”, e assegure-se que todos os alunos compreenderam a ideia.
Nos slides 9 a 12, apresente cada resposta aos alunos, perguntando sempre se eles responderam de maneira semelhante e pedindo também que alguns deles compartilhem suas resoluções. Aproveite que eles estarão com os triângulos em mãos para solicitar que eles mostrem neles as diagonais, lados congruentes e lados comuns.
Não esqueça de chamar a atenção dos estudantes para as nomenclaturas e definições formais.
Propósito: Compartilhar as resoluções da atividade e também avaliar e explicar algumas propriedades de paralelogramos e trapézios isósceles.
Discuta com a turma:
- Alguém pensou de forma diferente e chegou à mesma solução? Quais?
- Alguém pensou em outras possibilidades de solução? Quais? Por quê?
Discussão das Soluções

Tempo sugerido: 12 minutos. (Slides 8 a 13)
Orientações: No slides 8, apresente aos alunos as resoluções da atividade 1, questionando quem respondeu da mesma maneira apresentada. Caso algum aluno tenha respondido de maneira diferente ou traga diferentes argumentos, peça para que compartilhe em voz alta com seus colegas, para que todos possam juntos verificar a validade dos argumentos.
No slide 9, há a continuação das respostas, pergunte também se alguém respondeu de maneira semelhante ou diferentes ao que está nos slides e discuta com eles se es estratégias foram válidas ou não. No final do slide 9, ressalte o item “Relembrando”, e assegure-se que todos os alunos compreenderam a ideia.
Nos slides 9 a 12, apresente cada resposta aos alunos, perguntando sempre se eles responderam de maneira semelhante e pedindo também que alguns deles compartilhem suas resoluções. Aproveite que eles estarão com os triângulos em mãos para solicitar que eles mostrem neles as diagonais, lados congruentes e lados comuns.
Não esqueça de chamar a atenção dos estudantes para as nomenclaturas e definições formais.
Propósito: Compartilhar as resoluções da atividade e também avaliar e explicar algumas propriedades de paralelogramos e trapézios isósceles.
Discuta com a turma:
- Alguém pensou de forma diferente e chegou à mesma solução? Quais?
- Alguém pensou em outras possibilidades de solução? Quais? Por quê?
Discussão das Soluções

Tempo sugerido: 12 minutos. (Slides 8 a 13)
Orientações: No slides 8, apresente aos alunos as resoluções da atividade 1, questionando quem respondeu da mesma maneira apresentada. Caso algum aluno tenha respondido de maneira diferente ou traga diferentes argumentos, peça para que compartilhe em voz alta com seus colegas, para que todos possam juntos verificar a validade dos argumentos.
No slide 9, há a continuação das respostas, pergunte também se alguém respondeu de maneira semelhante ou diferentes ao que está nos slides e discuta com eles se es estratégias foram válidas ou não. No final do slide 9, ressalte o item “Relembrando”, e assegure-se que todos os alunos compreenderam a ideia.
Nos slides 9 a 12, apresente cada resposta aos alunos, perguntando sempre se eles responderam de maneira semelhante e pedindo também que alguns deles compartilhem suas resoluções. Aproveite que eles estarão com os triângulos em mãos para solicitar que eles mostrem neles as diagonais, lados congruentes e lados comuns.
Não esqueça de chamar a atenção dos estudantes para as nomenclaturas e definições formais.
Propósito: Compartilhar as resoluções da atividade e também avaliar e explicar algumas propriedades de paralelogramos e trapézios isósceles.
Discuta com a turma:
- Alguém pensou de forma diferente e chegou à mesma solução? Quais?
- Alguém pensou em outras possibilidades de solução? Quais? Por quê?
Sistematização do Conceito

Tempo sugerido: 2 minutos.
Orientações: Sistematize os principais conceitos aprendidos durante a aula, interpretando-os junto com os alunos de modo que eles possam retomá-los sempre que necessário.
Propósito: Sistematizar o conceito central estudado no decorrer da aula.
Encerramento
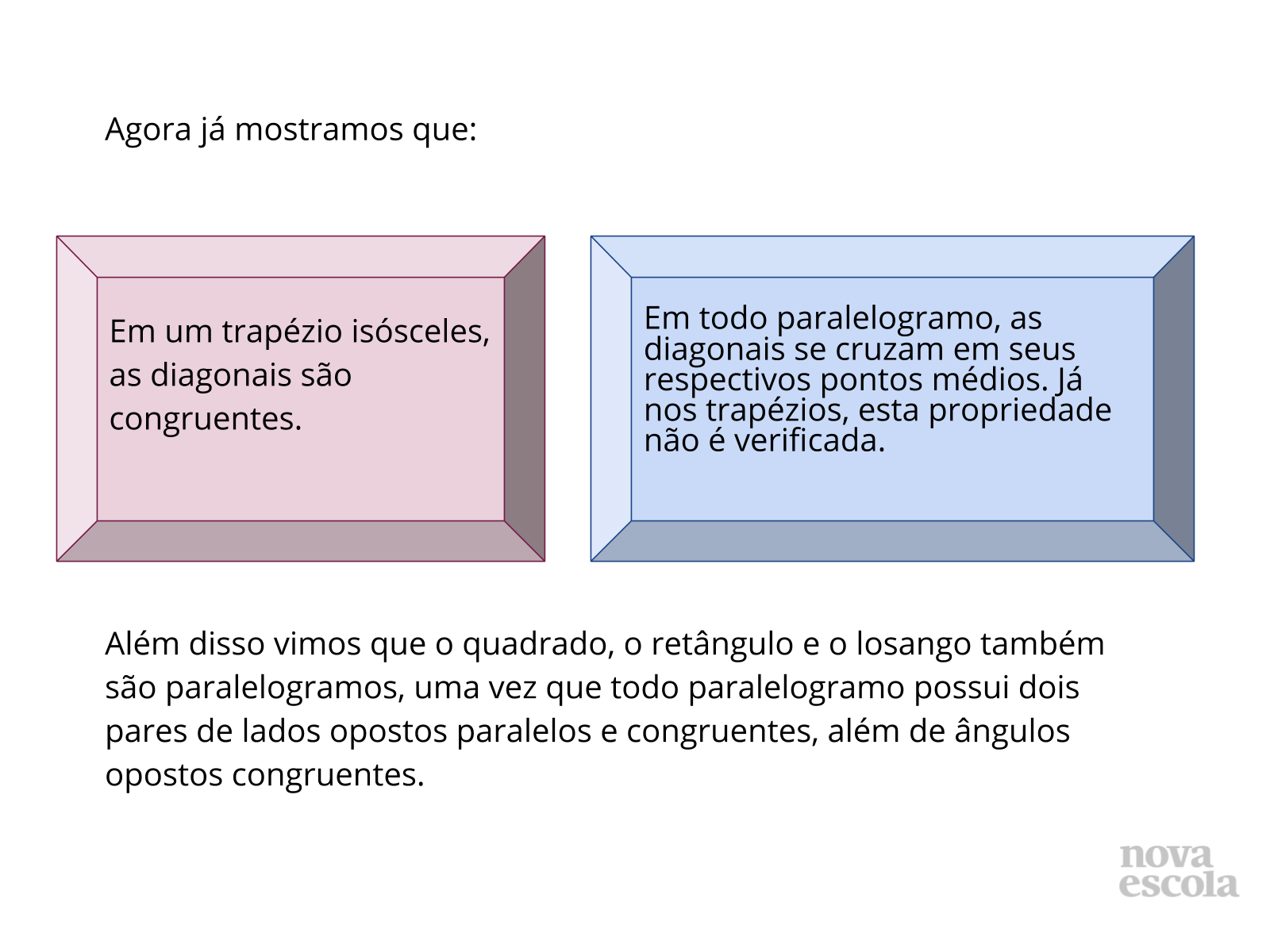
Tempo sugerido: 3 minutos.
Orientações: Encerre a atividade retomando com os estudantes as deduções realizadas por eles, as quais devem descrever as principais características dos paralelogramos e trapézios isósceles. Além disso, retome os questionamentos iniciais do Aquecimento para validar as hipóteses levantadas e sugira que eles escrevam em seu caderno uma espécie de glossário, no qual as aprendizagens possam ser anotadas.
Propósito: Sintetizar os resultados desenvolvidos ao longo da aula em relação às principais características dos trapézios e paralelogramos
Materiais Complementares:
Caso queira se aprofundar nas definições e demonstrações, acesse https://docs.ufpr.br/~roman/files/GA2.pdf
Raio x
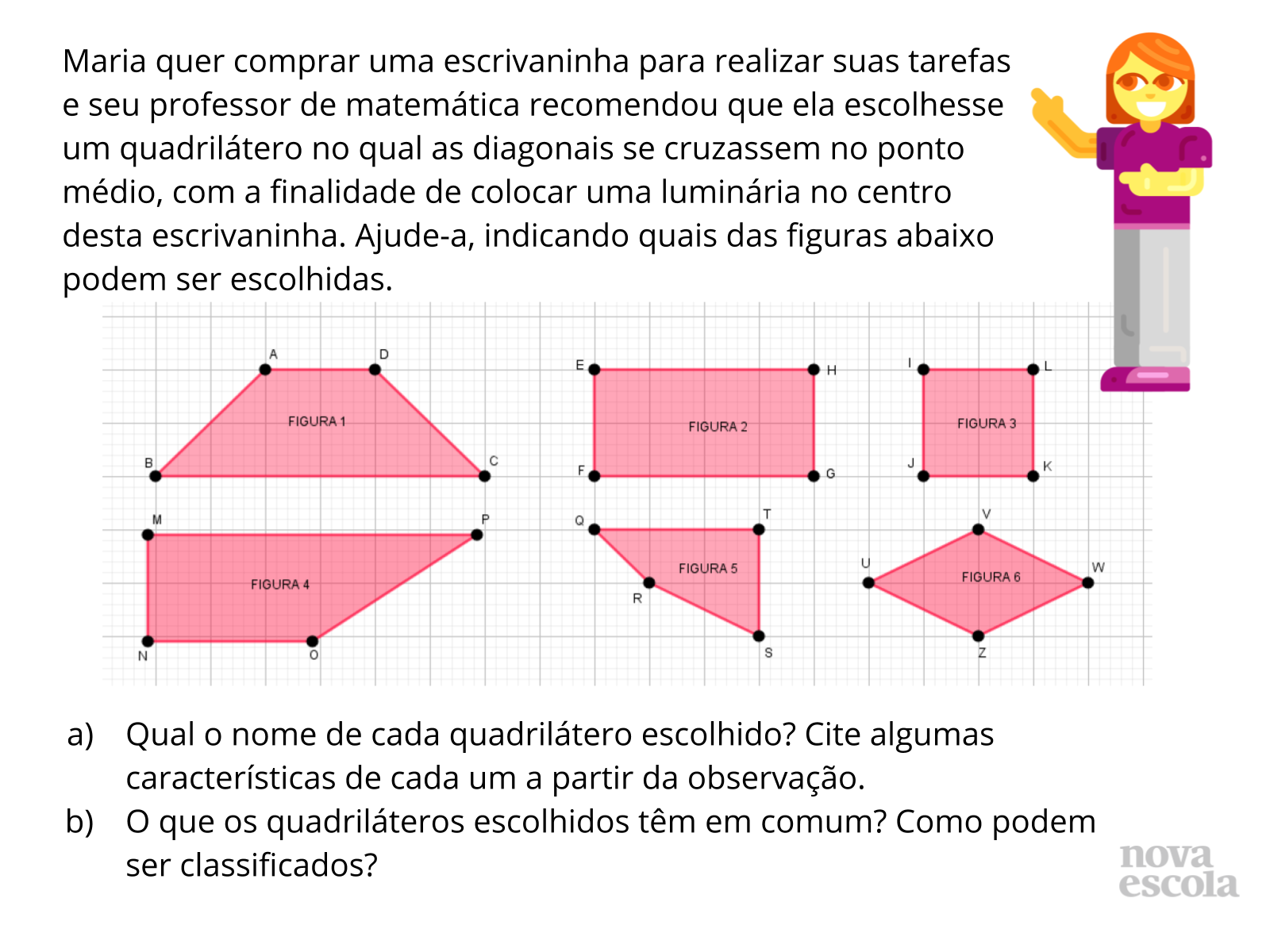
Tempo sugerido: 10 minutos.
Orientações: Peça que os alunos leiam e resolvam a atividade individualmente. Em seguida, peça que discutam com um colega suas soluções, com o objetivo de confrontar suas hipóteses, de modo a validá-las ou refutá-las. Se necessário, sugira que os estudantes utilizem as imagens dos quadriláteros e tracem suas diagonais, a fim de testar e validar suas hipóteses. Também pode ser sugerido que recortem os quadriláteros e sobreponham as partes, a fim de verificar, por congruência de triângulos, a solução da atividade. Ao final da atividade, realize uma roda conversa para fechamento da aula análise do que foi aprendido.
Propósito: Verificar se o objetivo de investigar as propriedades dos paralelogramos e trapézios isósceles utilizando a congruência de triângulos foi alcançado pelo aluno.
Discuta com a turma:
- Quais são os quadriláteros representados em cada figura?
- Qual o nome de cada quadrilátero escolhido? E quais as suas principais características?
- O que os quadriláteros escolhidos têm em comum? Como podem ser classificados?
- Por que o trapézio isósceles não foi escolhido?
Materiais complementares para impressão:
Para o aluno
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano
MAT8_16GEO02
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: Papel, lápis, WhatsApp
- Opcionais: Messenger Sala de aluno ( https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/), Meet, Hangout, Zoom, plataforma da Khan Academy ( https://pt.khanacademy.org/)
Portal OBMEP ( https://portaldaobmep.impa.br/index.php/modulo/lista?serie=3)
Geogebra https://play.google.com/store/apps/details?id=org.geogebra&hl=pt_BR
Para este plano, foque na etapa ATIVIDADE PRINCIPAL
Aquecimento
Sugerimos foco na Atividade principal.
Atividade principal
A atividade principal trata de muitos conceitos que necessitam conhecimentos prévios específicos. Sugerimos usar inicialmente apenas a questão 1, propondo uma ‘aula invertida’. Assim, você deve disponibilizar aos alunos a questão 1 e os slides das soluções (1 e 2). Grave um vídeo ou áudio orientando a proposta e solicitando que os alunos analisem a situação e as respectivas discussões das soluções, procurando explicar através de um vídeo curto o entendimento da situação. Você pode acrescentar mais informações que julgar pertinente para auxiliar os alunos em suas produções (ver Encerramento e Sistematização do conceito). A turma deve encaminhar (via WhatsApp) o vídeo para sua apreciação. Mantenha um canal de comunicação permanente para dúvidas e sugestões. Posteriormente, você pode solicitar a realização da 2ª questão da Atividade principal e também o Raio X e atividades complementares.
Na plataforma da Khan Academy há vários vídeos e demais recursos que tratam de quadriláteros. Você pode selecionar os materiais pertinentes e indicar aos alunos que possuem acesso à internet.
https://pt.khanacademy.org/math/geometry-home/quadrilaterals-and-polygons
No Portal da OBMEP há exploração dos elementos básicos da geometria plana (partes 1, 2 e 3) que pode servir de apoio aos alunos que possuem internet.
https://portaldaobmep.impa.br/index.php/modulo/lista?serie
Discussão das soluções
Essa proposta de atividade exige idas e vindas nas discussões. Retome os vídeos dos alunos para dar um feedback (áudio ou vídeo) considerando os equívocos, acertos e dúvidas. Use informações do Encerramento e da Sistematização do conceito. Se sua turma dispuser de ferramentas e internet, dê preferência por realizar as discussões em tempo real, por meio de uma das plataformas sugeridas abaixo. Se não tiver, use o WhatsApp que tem um alcance maior. Mas, não esqueça de manter um canal de comunicação para discussão e também de sugerir a realização das demais atividades desse plano (atividades complementares e Raio X).
Se for possível discutir em tempo real com sua turma, use o Meet, Hangout ou Zoom e considere apenas os itens e os conceitos de maior relevância.
Você pode usar também o Messenger Sala de aluno https://www.messenger.com/groupcall/LINK:4svjhs7dyZw8zoxm/.
Sistematização
Use nas orientações e/ou discussões.
Encerramento
Use nas orientações e/ou discussões.
Raio X
Use o Raio X como complemento à Atividade principal. Não esqueça também de propor a realização das atividades complementares.
Convite às famílias
Pode-se discutir sobre diagonais: elas serão maiores ou menores que os lados das figuras?
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Geisa Zilli Shinkawa da Silva
Mentor: Fabrício Eduardo Ferreira
Especialista de área: Pricilla Cerqueira
Habilidade da BNCC
EF08MA12 - Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.
Objetivos específicos
Investigar as propriedades dos paralelogramos, dos trapézios e trapézios isósceles, utilizando congruência de triângulos. Identificar as principais características dos quadriláteros e suas propriedades, além de reconhecer quadrados, retângulos e losangos como paralelogramos.
Conceito-chave
Propriedades de quadriláteros.
Recursos necessários
- Lápis de escrever, lápis de cor, borracha e tesoura;
- Esquadros e régua;
- Folha de papel A4 (para desenho e recorte);
- Atividades impressas (preferencialmente) ou projetadas.