Sugestão de adaptaçãopara ensino remoto
Código do plano
MAT6_18GEO05
Recursos
- Necessários: Folha sulfite, lápis, caderno, régua
- Opcionais: Meet, Zoom, WhatsApp, padlet, malha quadriculada
Tipos de isometrias: http://blogmatematic.blogspot.com/2012/01/isometrias-reflexao-rotacao-e.html
Introdução a simetria de reflexão: https://pt.khanacademy.org/math/basic-geo/basic-geo-transformations-congruence/line-of-symmetry/v/axis-of-symmetry
Para este plano, foque na etapa: Atividade Principal
Aquecimento
Aproveite a imagem do espelho e solicite que os alunos ou peguem um espelho que tenham em casa ou fiquem diante de um espelho. Converse com eles sobre como é nosso reflexo no espelho. Quando levantamos o braço direito, nosso reflexo levanta o esquerdo. Introduzir o conceito de simetria. Nosso reflexo é exatamente igual a nós, são imagens simétricas. Convide o aluno a fazer esse experimento em casa e anotar no caderno as suas conclusões.
Atividade Principal (adaptada)
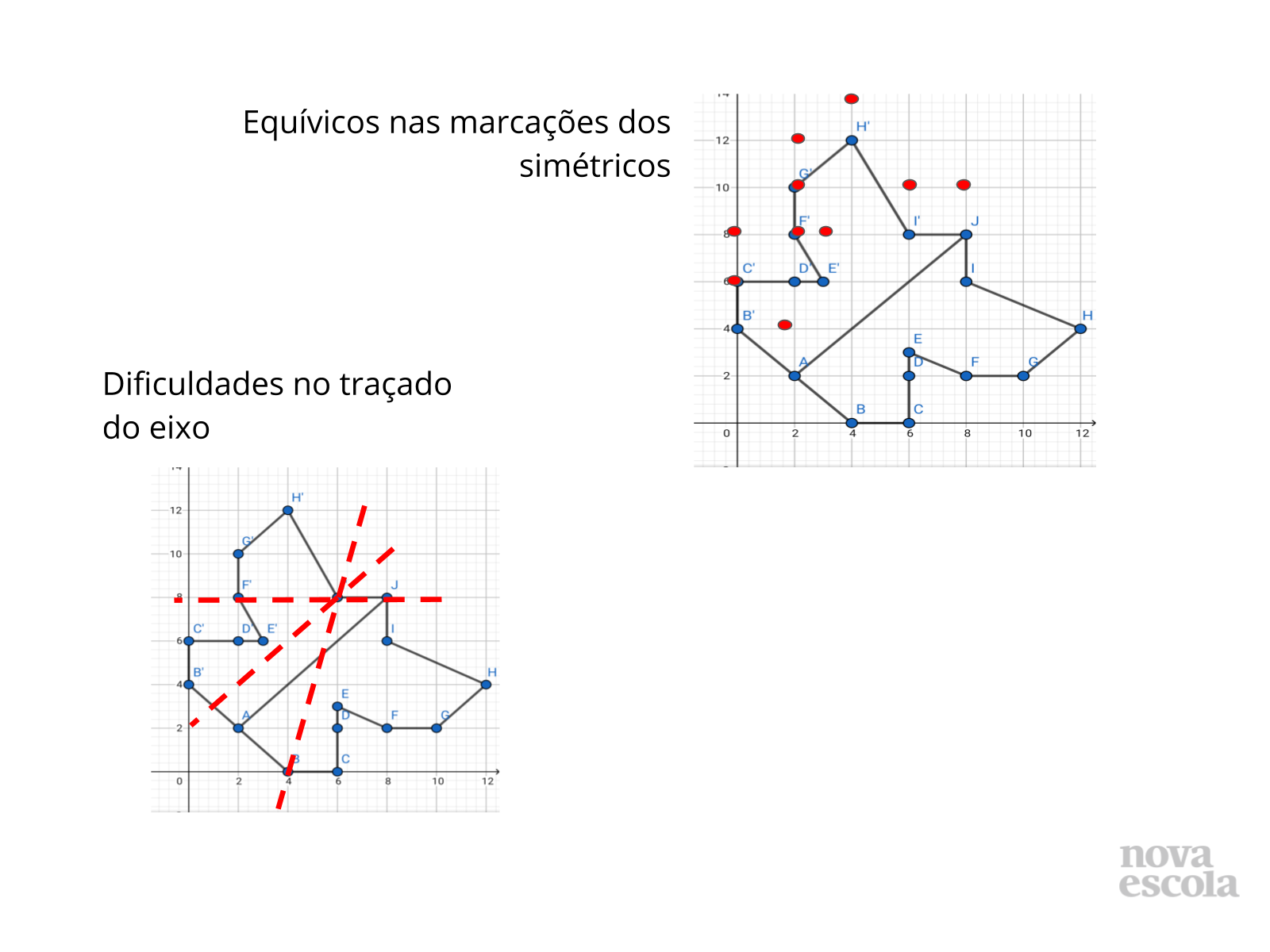
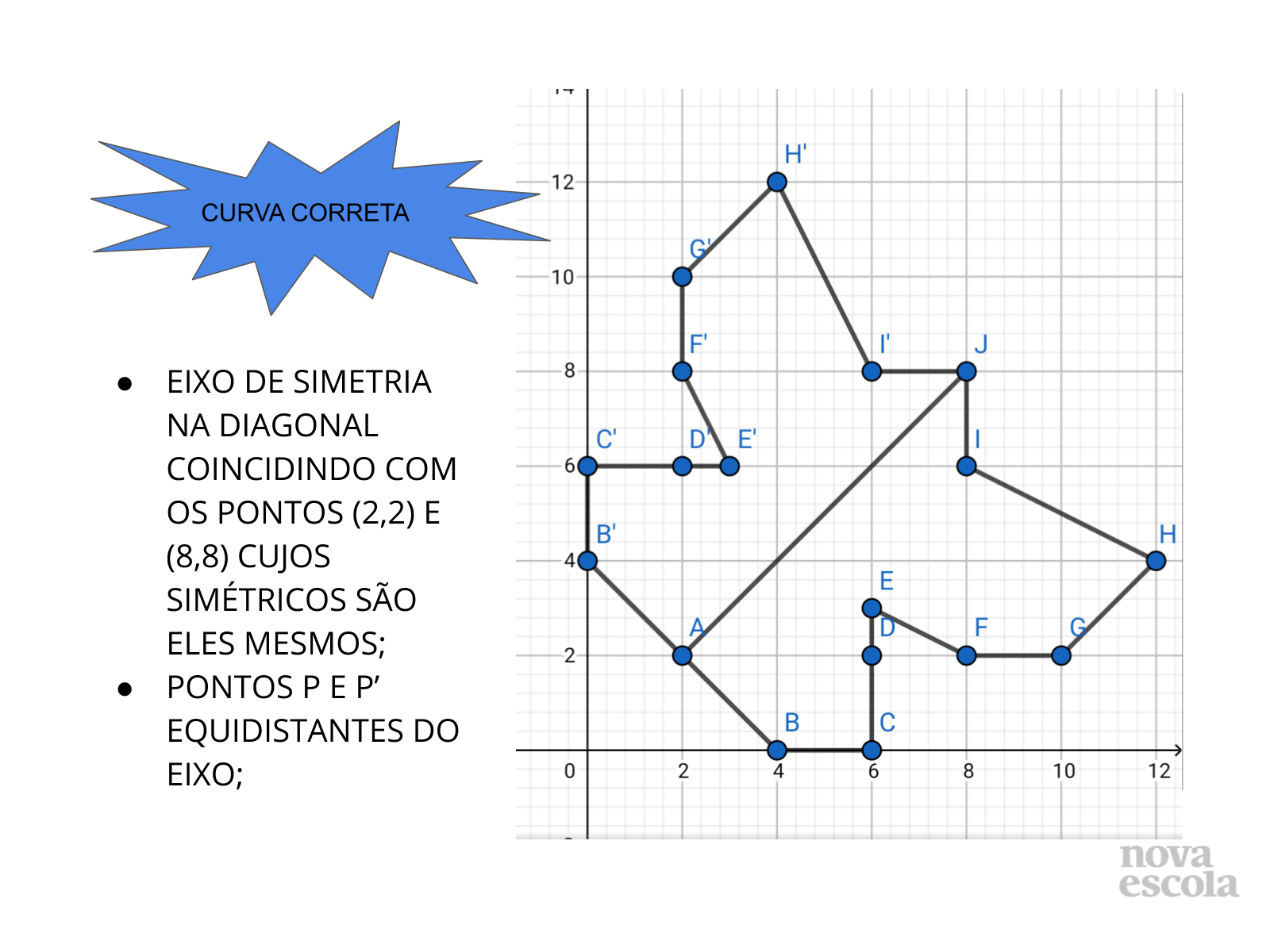
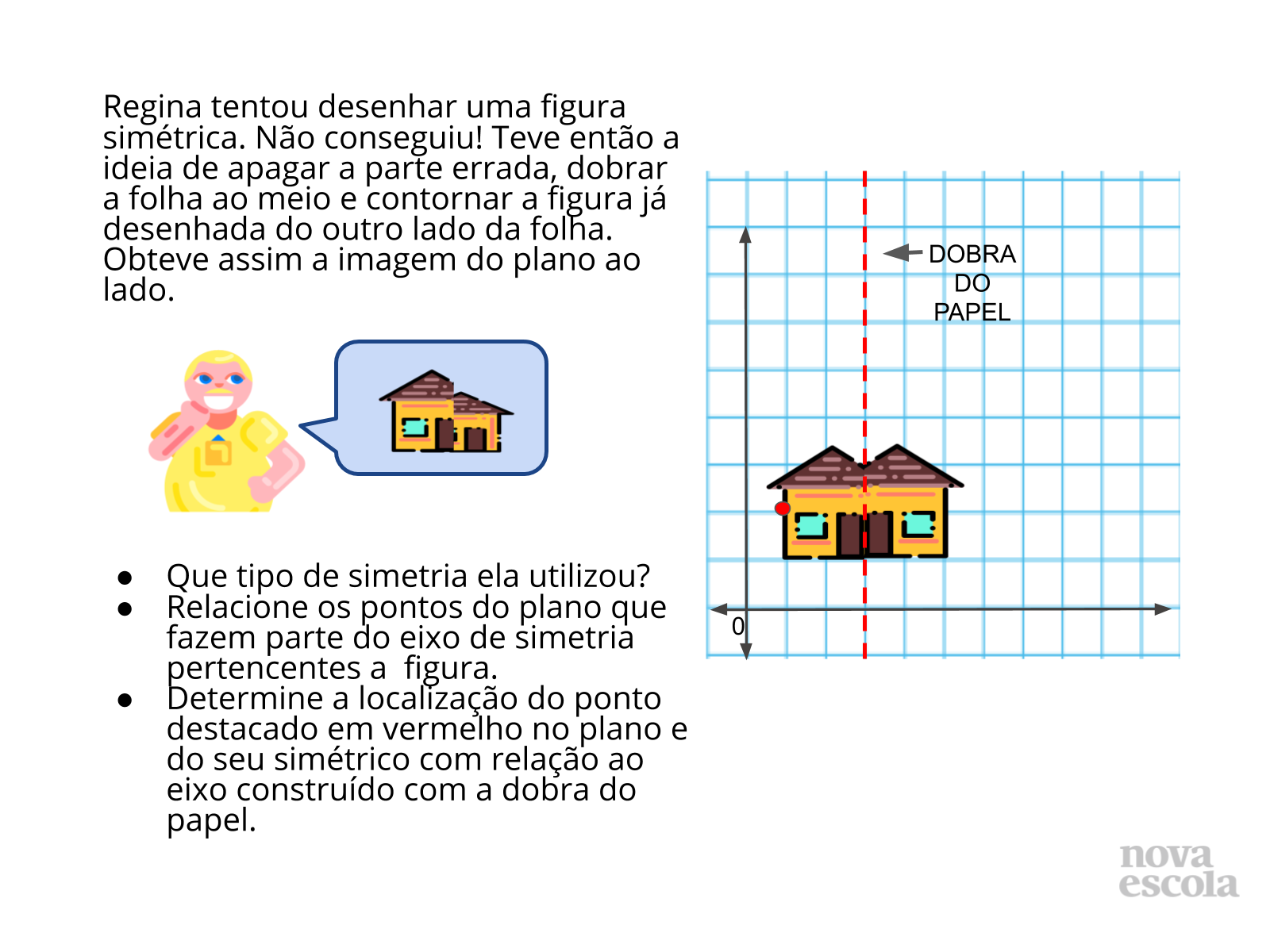
Você pode fazer uma sala de aula invertida. Compartilhe com os alunos o “Roteiro da Atividade Principal” pelo meio de comunicação combinado entre vocês (Meet, hangouts, Zoom, WhatasApp). Se eles não puderem imprimir o plano cartesiano, podem desenhar no caderno utilizando a régua. Oriente-os quanto ao roteiro. Se achar necessário, grave um áudio explicando e dando orientações de como realizá-lo. No dia marcado, abra o áudio e escute as possíveis dúvidas ou aprendizagens. O desafio para os alunos é perceber que a inversão dos elementos dos pontos determinados através do roteiro, além de corresponder a pontos totalmente diferentes no plano, formam uma curva simétrica a construída anteriormente. Logo existe uma relação entre os pontos equivalentes nas duas curvas. Eles são equidistantes de um eixo determinado pela própria construção. Questione: Por que é importante a construção de um eixo? O que significa os pontos serem equidistantes desse eixo? Esses pontos são simétricos? Também é possível que eles possam ter tido dúvidas quanto ao preenchimento da tabela. Por isso que a escuta e o compartilhamento de ideias nessa hora é de fundamental importância para que a aprendizagem se torne efetiva. Faça o “Discuta com a turma” que orienta os alunos a pensar sobre como fizeram e a analisar suas próprias hipóteses. Sugira que ao final, eles cortem a figura e dobrem ao meio para verificar o que acontece e tirar conclusões.
Encerramento
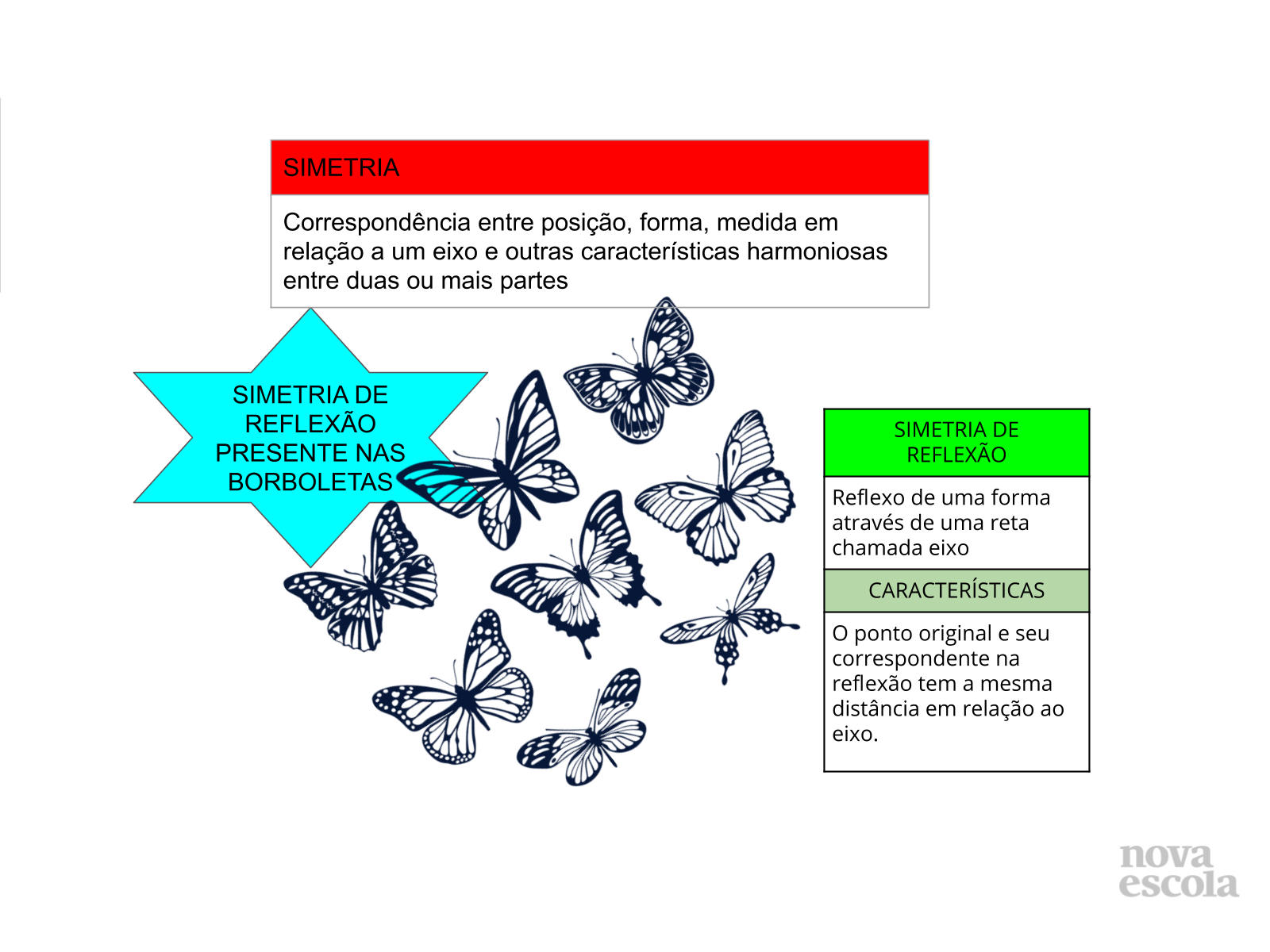
Compartilhe o slide de encerramento para fechar as ideias discutidas na aula.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
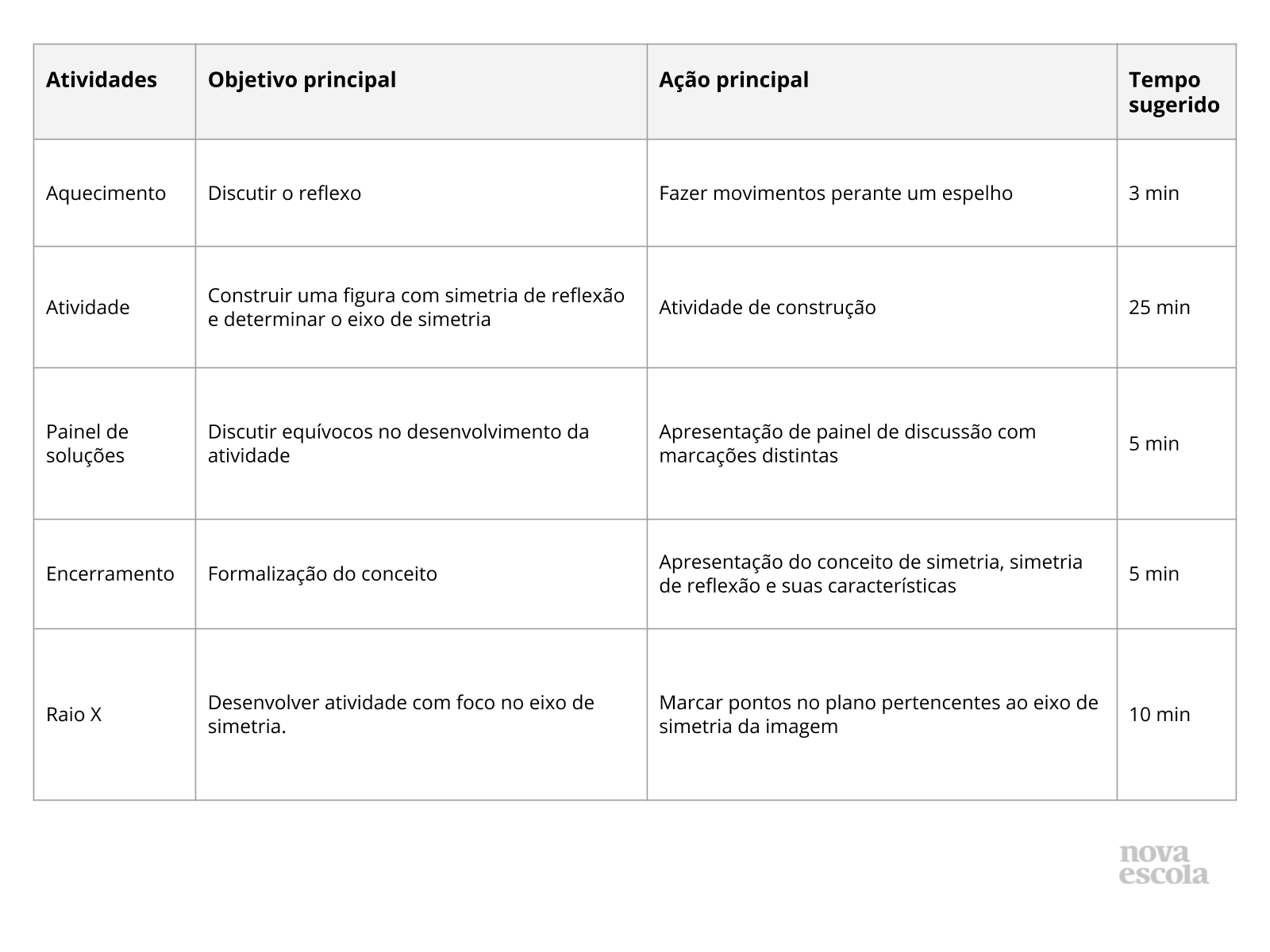 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.