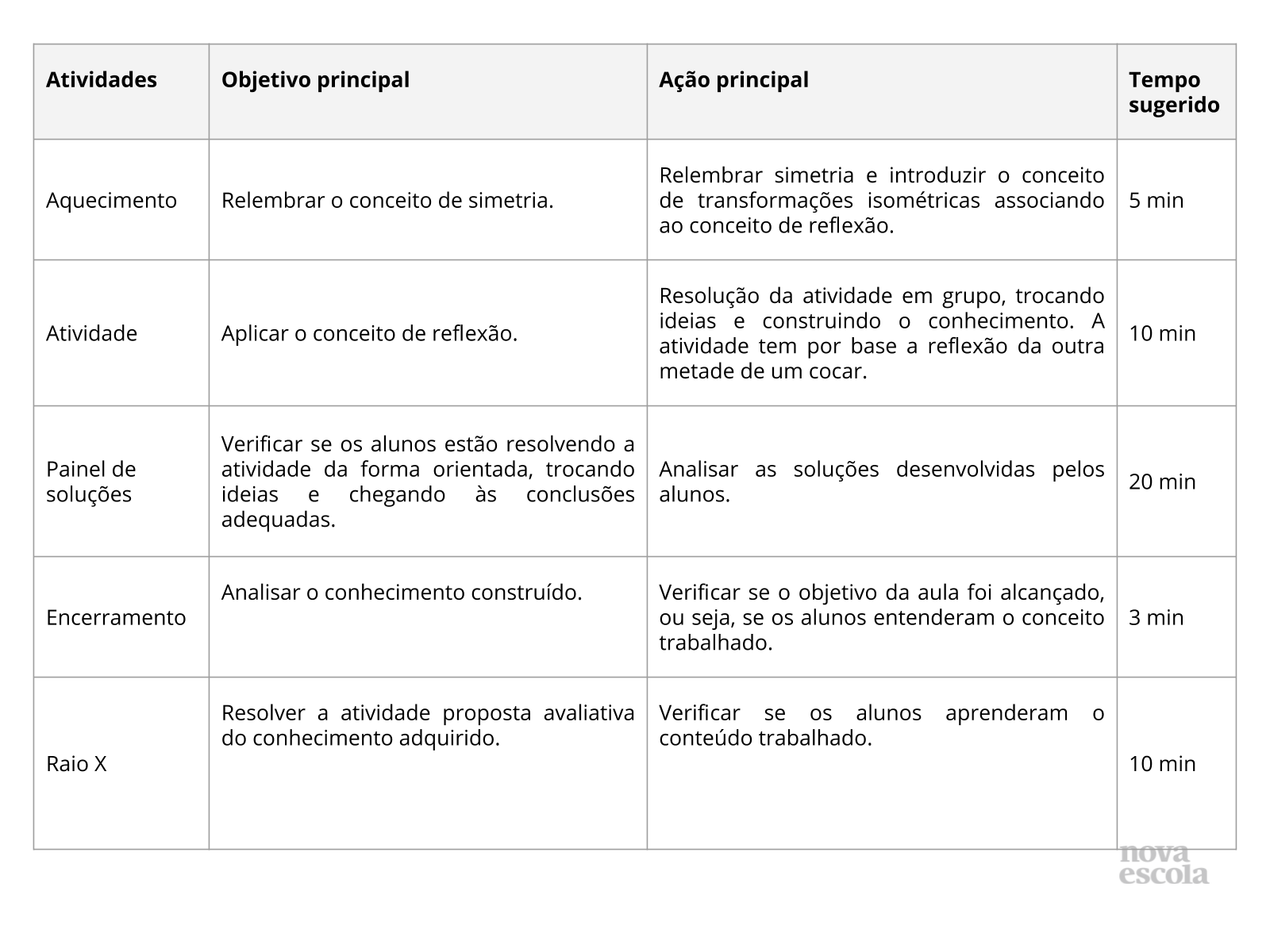
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
OBJETIVO

Tempo sugerido: 2 minutos
Orientação: Compartilhar com a turma o objetivo da aula.
Propósito: Apresentar o objetivo da aula para a turma.
Aquecimento
Tempo sugerido: 2 minutos.
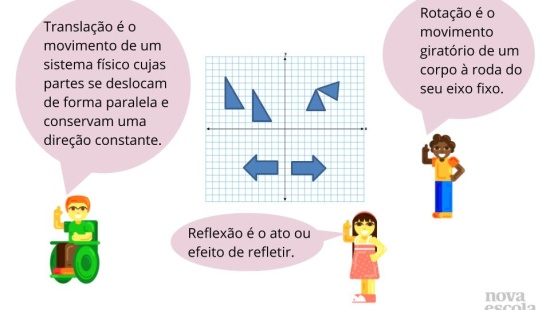
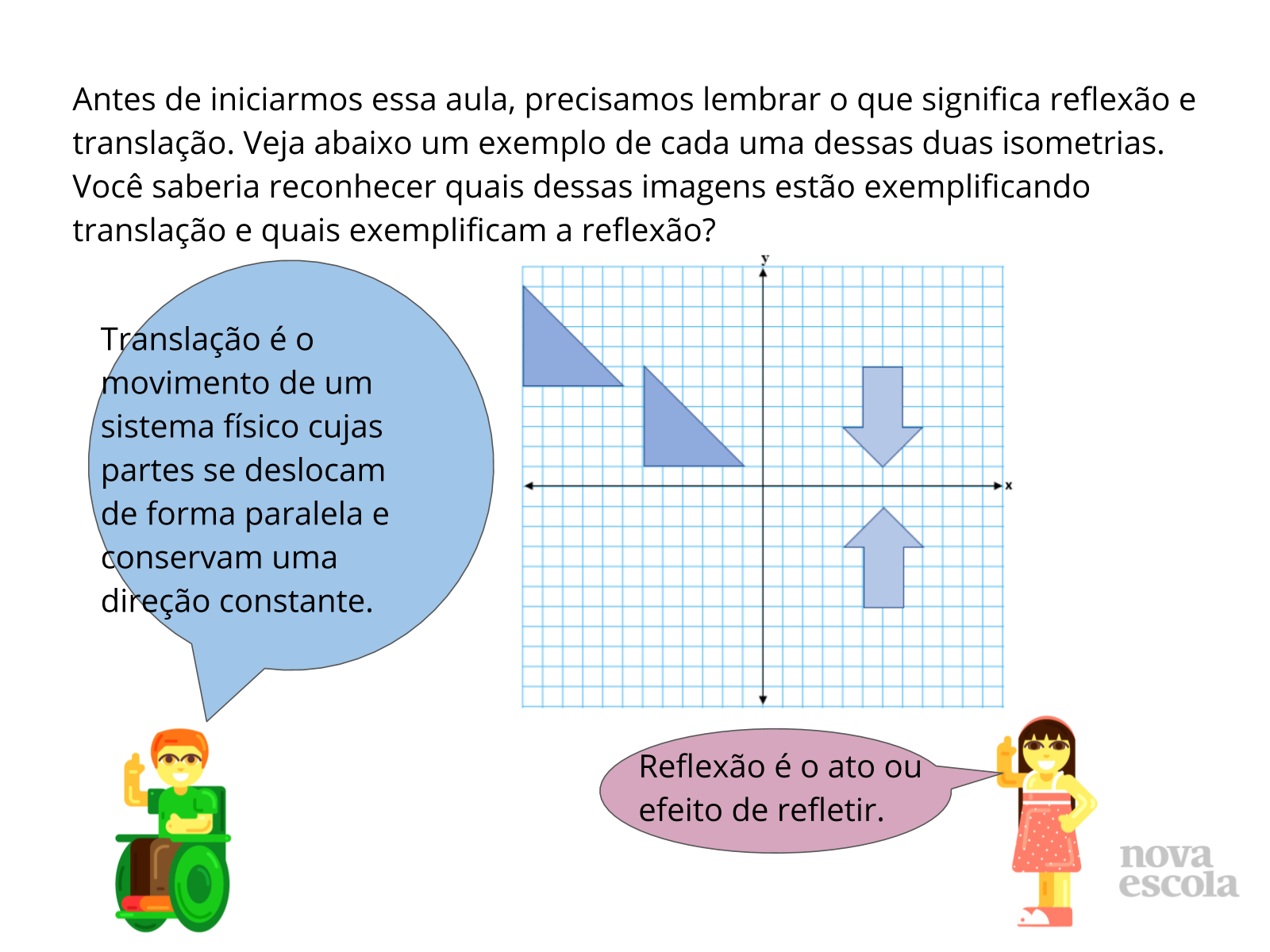
Orientação: Lembrar o que é reflexão e o que é translação, uma vez que a reflexão deslizante é conteúdo desta aula, é a junção dessas duas isometrias.
Propósito: Relembrar simetria de reflexão e simetria de translação.
Atividade principal
Tempo sugerido: 15 minutos (slides 4 e 5)
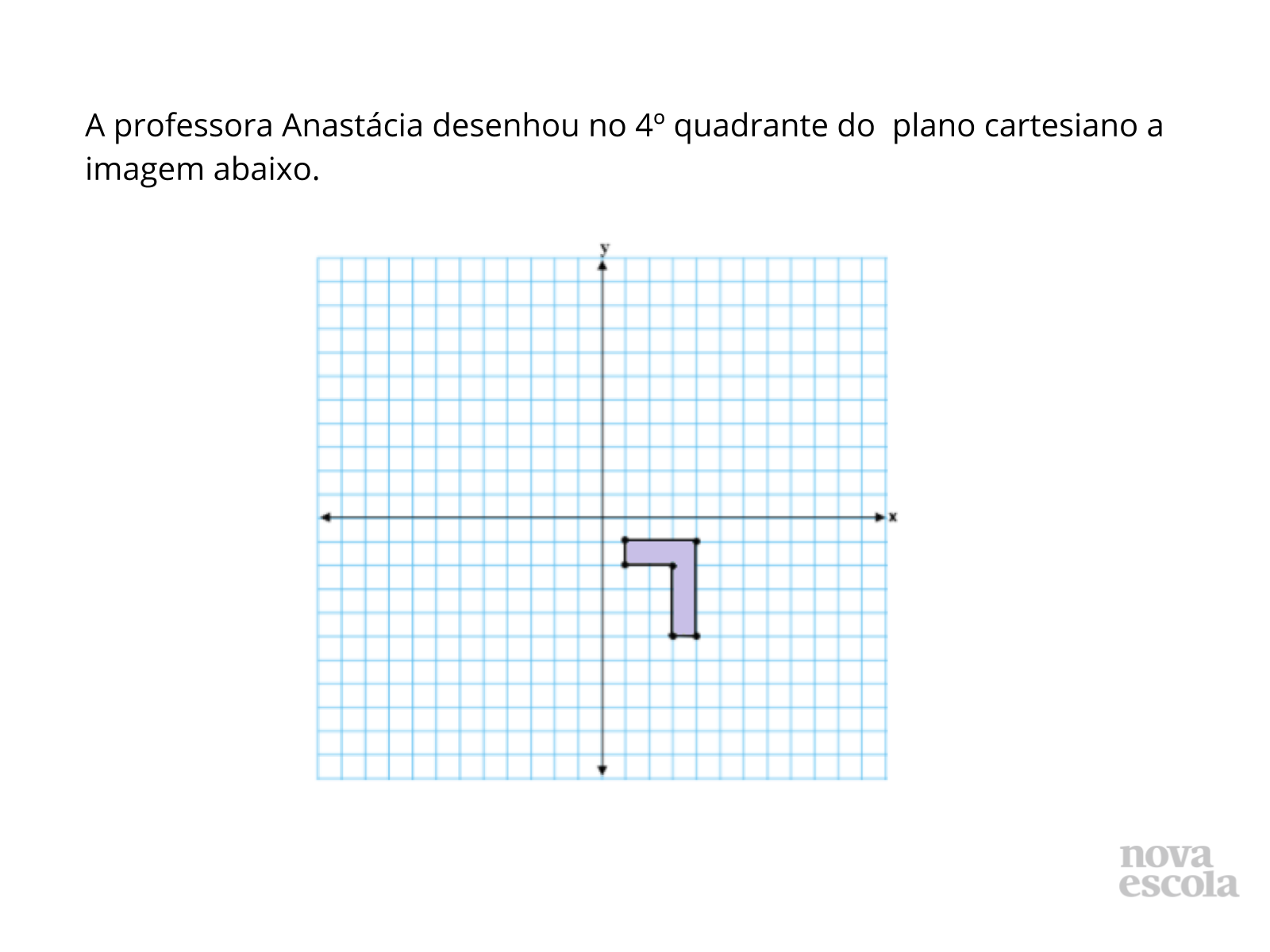
Orientação: Solicitar que em grupos a turma discuta a questão. Cada aluno do grupo pode marcar o simétrico de um dos 6 pontos para fazer a reflexão no terceiro quadrante. Em seguida, cada aluno poderá marcar um ponto para fazer a translação da imagem para o quarto quadrante.
Propósito: Ensinar aos alunos o que é isometria de reflexão deslizante, mostrar que é uma reflexão junto com uma translação.
Discuta com a turma:
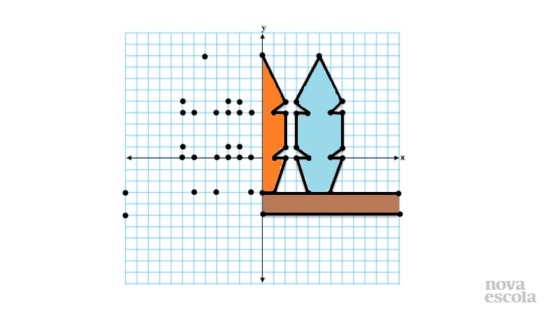
1) Quais as coordenadas dos vértices da imagem?
2) O que devemos fazer para refletir a imagem no terceiro quadrante? Quais serão as coordenadas dos novos pontos?
3) Como devemos proceder para transladar a imagem para o quarto quadrante? Quais serão as coordenadas dos novos pontos para que forme uma nova letra com a imagem desenhada pela professora no quarto quadrante?
4) Ao fazer esta translação, qual coordenada de cada ponto sofreu alteração? Aumentou ou diminuiu? Quantas unidades?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade principal

Tempo sugerido: 15 minutos (slides 4 e 5)
Orientação: Solicitar que em grupos a turma discuta a questão. Cada aluno do grupo pode marcar o simétrico de um dos 6 pontos para fazer a reflexão no terceiro quadrante. Em seguida, cada aluno poderá marcar um ponto para fazer a translação da imagem para o quarto quadrante.
Propósito: Ensinar aos alunos o que é isometria de reflexão deslizante, mostrar que é uma reflexão junto com uma translação.
Discuta com a turma:
1) Quais as coordenadas dos vértices da imagem?
2) O que devemos fazer para refletir a imagem no terceiro quadrante? Quais serão as coordenadas dos novos pontos?
3) Como devemos proceder para transladar a imagem para o quarto quadrante? Quais serão as coordenadas dos novos pontos para que forme uma nova letra com a imagem desenhada pela professora no quarto quadrante?
4) Ao fazer esta translação, qual coordenada de cada ponto sofreu alteração? Aumentou ou diminuiu? Quantas unidades?
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Discussão da solução
Tempo sugerido: 15 minutos (slides 6 a 10)
Orientação: Solicitar que em grupos de 6 alunos a turma discuta a questão. Cada aluno do grupo pode marcar um dos 6 pontos da reflexão a ser feita e, em seguida, um dos 6 pontos da translação.
Propósito: Levar o aluno a pensar como fazer a reflexão e a translação de uma imagem.
Discuta com a turma:
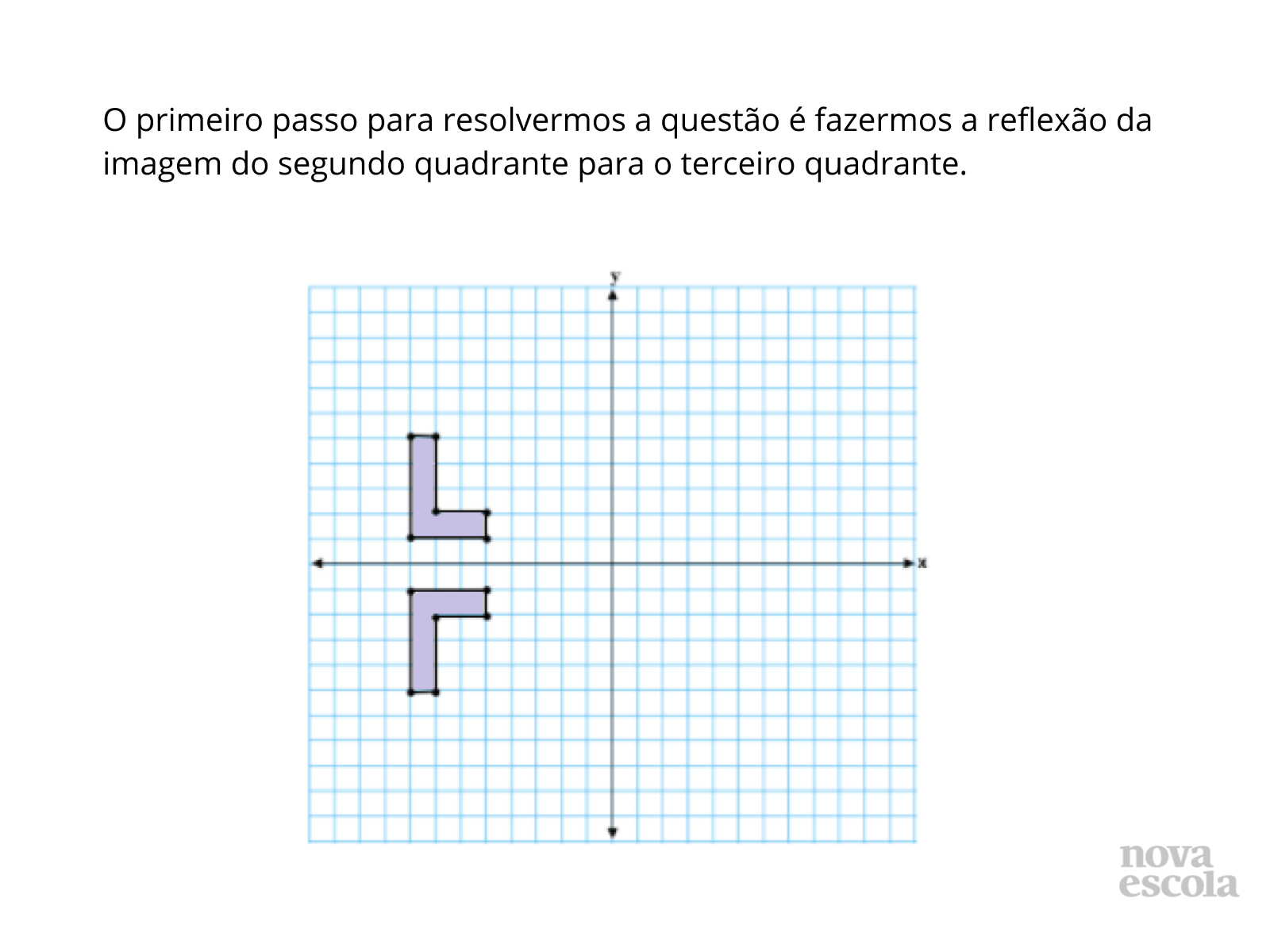
- Qual a letra desenhada no segundo quadrante do plano cartesiano?
- Como proceder para fazermos a reflexão da imagem no terceiro quadrante? A que distância cada ponto deverá estar do eixo x? E do eixo y?
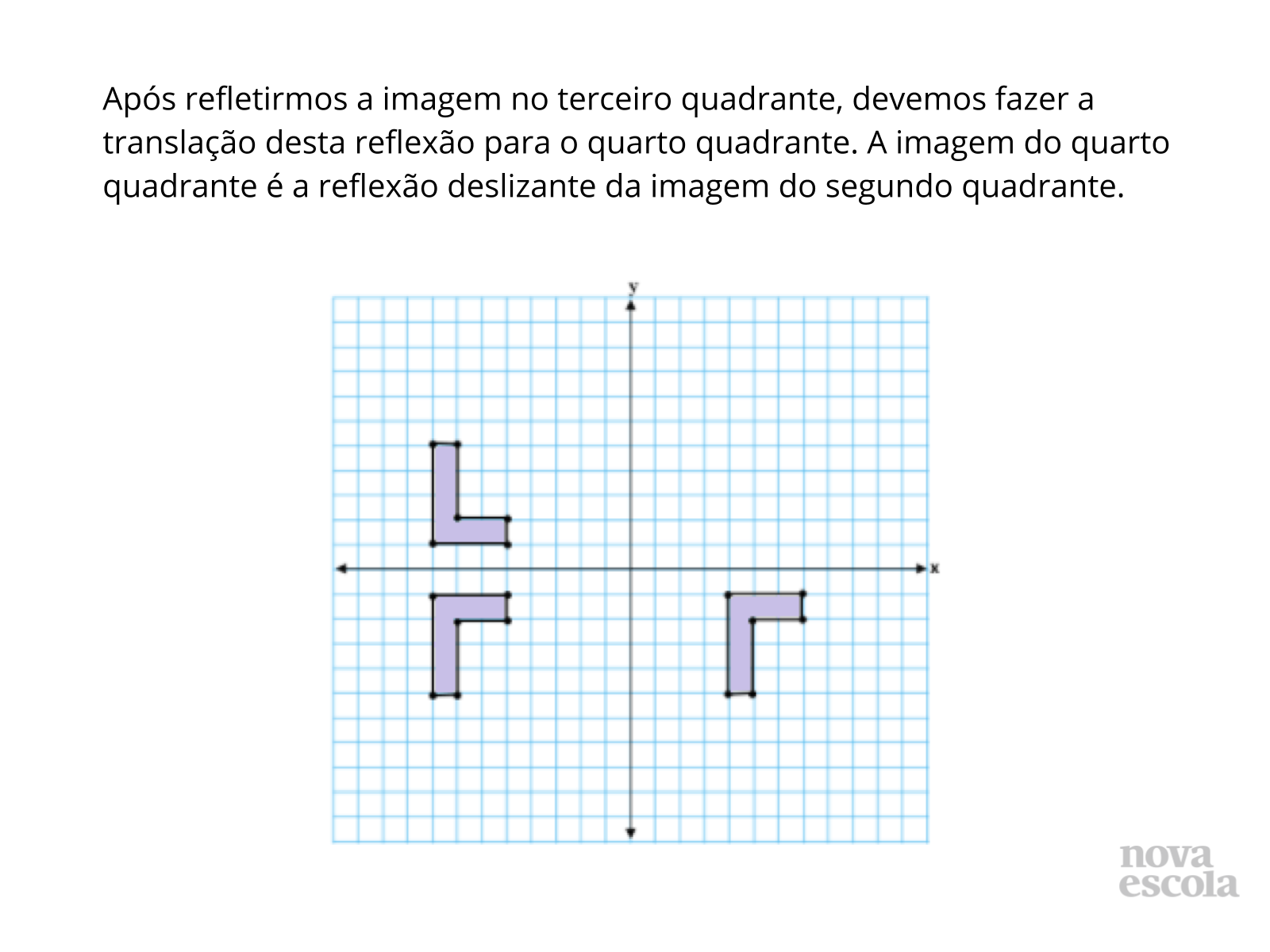
- Como proceder para fazer a translação da figura refletida para o quarto quadrante? Quantas unidades devemos aumentar no eixo x?
- Qual a diferença entre reflexão e translação?
Discussão da solução
Tempo sugerido: 15 minutos (slides 6 a 10)
Orientação: Solicitar que em grupos de 6 alunos a turma discuta a questão. Cada aluno do grupo pode marcar um dos 6 pontos da reflexão a ser feita e, em seguida, um dos 6 pontos da translação.
Propósito: Levar o aluno a pensar como fazer a reflexão e a translação de uma imagem.
Discuta com a turma:
- Qual a letra desenhada no segundo quadrante do plano cartesiano?
- Como proceder para fazermos a reflexão da imagem no terceiro quadrante? A que distância cada ponto deverá estar do eixo x? E do eixo y?
- Como proceder para fazer a translação da figura refletida para o quarto quadrante? Quantas unidades devemos aumentar no eixo x?
- Qual a diferença entre reflexão e translação?
Discussão da solução
Tempo sugerido: 15 minutos (slides 6 a 10)
Orientação: Solicitar que em grupos de 6 alunos a turma discuta a questão. Cada aluno do grupo pode marcar um dos 6 pontos da reflexão a ser feita e, em seguida, um dos 6 pontos da translação.
Propósito: Levar o aluno a pensar como fazer a reflexão e a translação de uma imagem.
Discuta com a turma:
- Qual a letra desenhada no segundo quadrante do plano cartesiano?
- Como proceder para fazermos a reflexão da imagem no terceiro quadrante? A que distância cada ponto deverá estar do eixo x? E do eixo y?
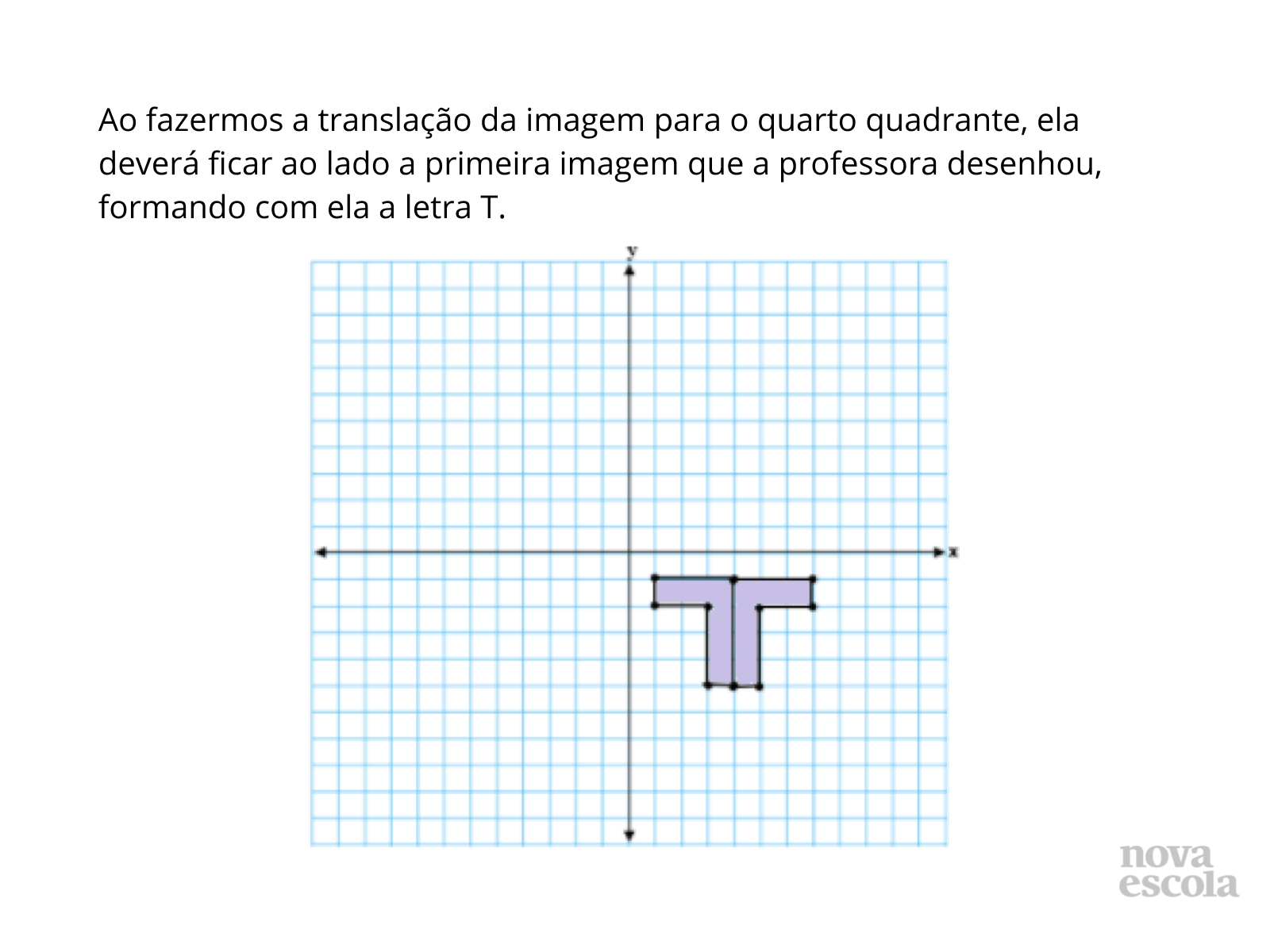
- Como proceder para fazer a translação da figura refletida para o quarto quadrante? Quantas unidades devemos aumentar no eixo x?
- Qual a diferença entre reflexão e translação?
Discussão da solução
Tempo sugerido: 15 minutos (slides 6 a 10)
Orientação: Solicitar que em grupos de 6 alunos a turma discuta a questão. Cada aluno do grupo pode marcar um dos 6 pontos da reflexão a ser feita e, em seguida, um dos 6 pontos da translação.
Propósito: Levar o aluno a pensar como fazer a reflexão e a translação de uma imagem.
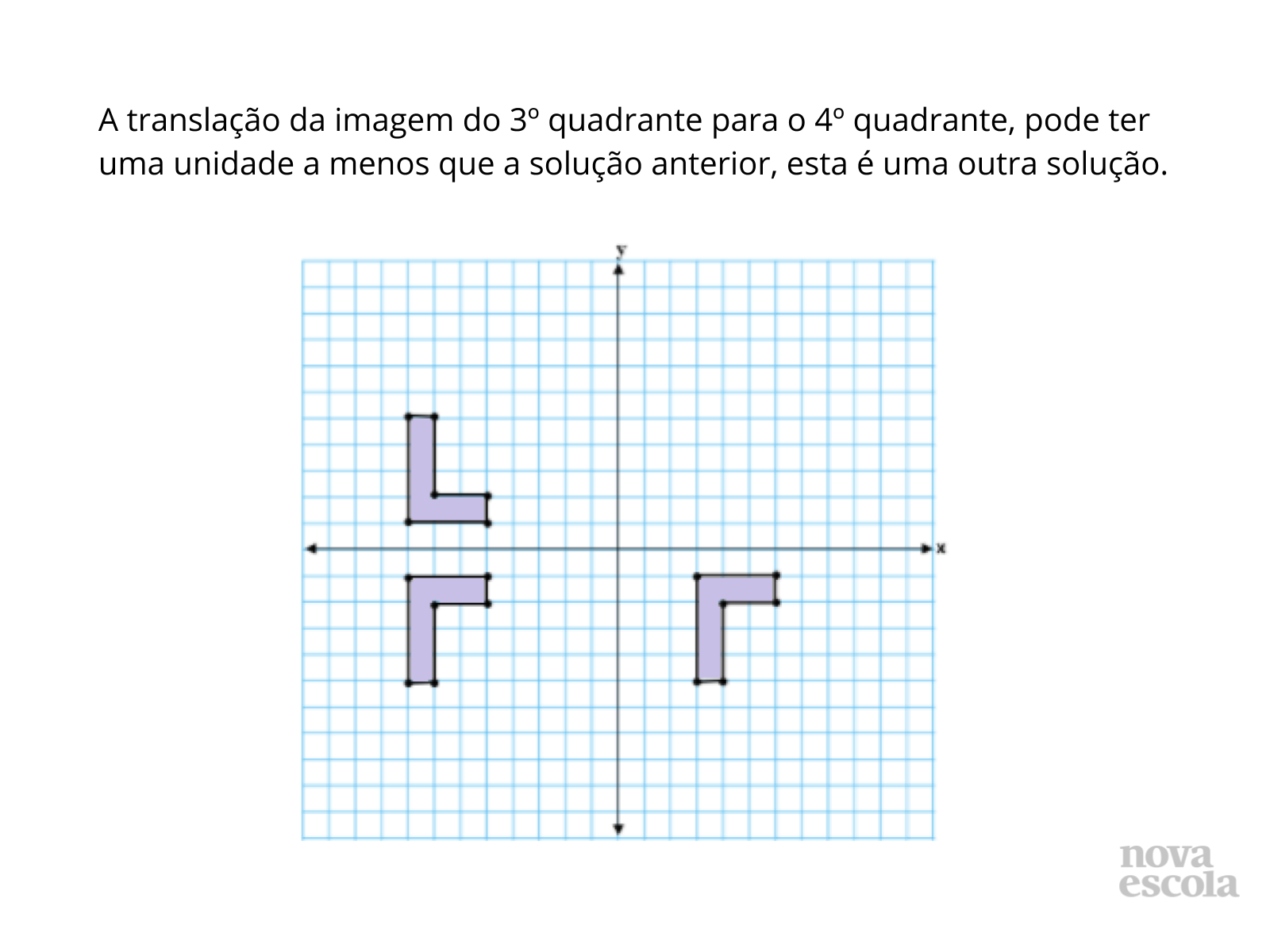
Discuta com a turma:
- Qual a letra desenhada no segundo quadrante do plano cartesiano?
- Como proceder para fazermos a reflexão da imagem no terceiro quadrante? A que distância cada ponto deverá estar do eixo x? E do eixo y?
- Como proceder para fazer a translação da figura refletida para o quarto quadrante? Quantas unidades devemos aumentar no eixo x?
- Qual a diferença entre reflexão e translação?
Discussão da solução

Tempo sugerido: 15 minutos (slides 6 a 10)
Orientação: Solicitar que em grupos de 6 alunos a turma discuta a questão. Cada aluno do grupo pode marcar um dos 6 pontos da reflexão a ser feita e, em seguida, um dos 6 pontos da translação.
Propósito: Levar o aluno a pensar como fazer a reflexão e a translação de uma imagem.
Discuta com a turma:
- Qual a letra desenhada no segundo quadrante do plano cartesiano?
- Como proceder para fazermos a reflexão da imagem no terceiro quadrante? A que distância cada ponto deverá estar do eixo x? E do eixo y?
- Como proceder para fazer a translação da figura refletida para o quarto quadrante? Quantas unidades devemos aumentar no eixo x?
- Qual a diferença entre reflexão e translação?
Encerramento
Tempo sugerido: 1 minuto
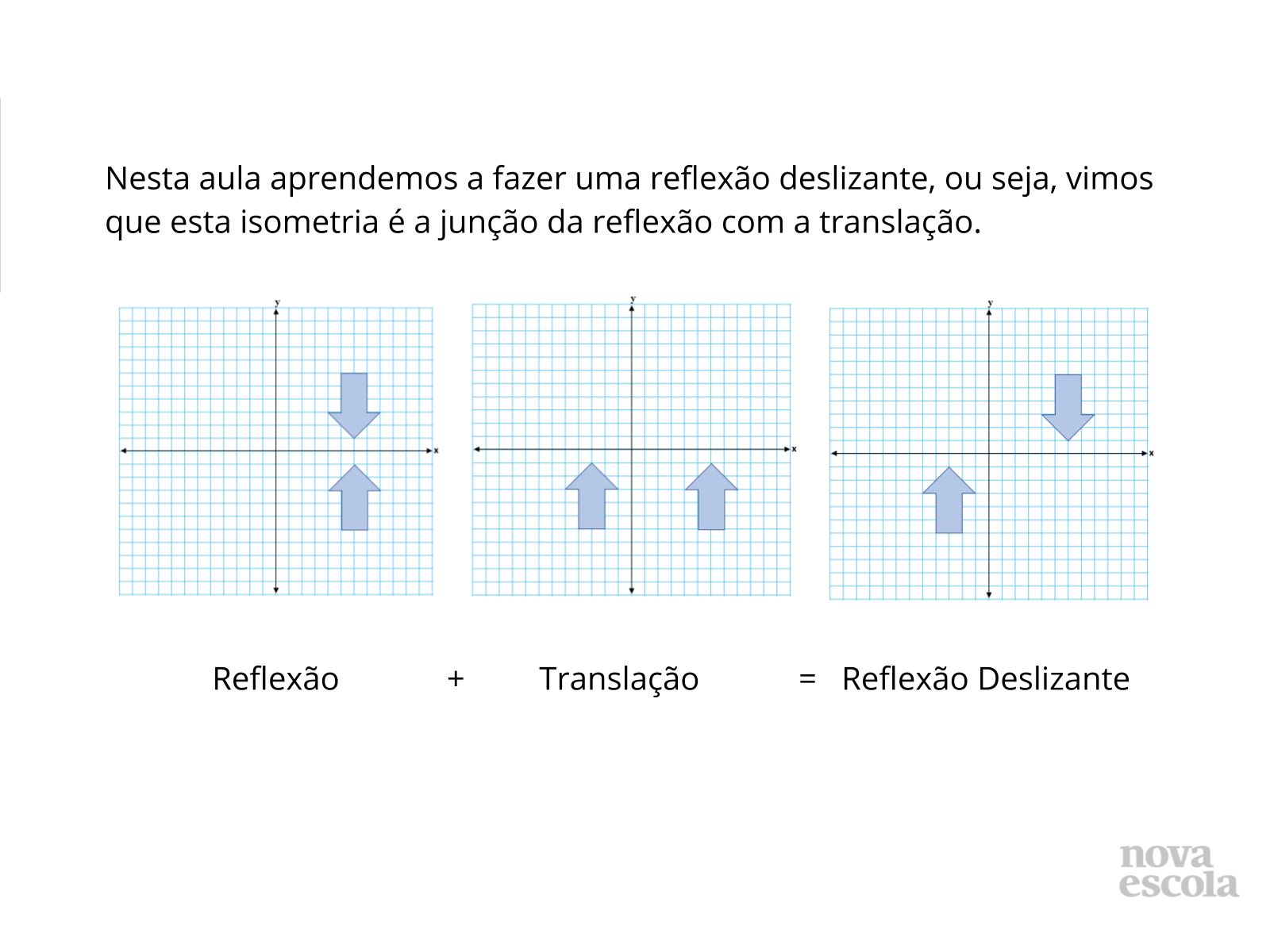
Orientação: Encerrar a aula frisando o conceito de reflexão deslizante.
Propósito: Realizar um fechamento das ideias discutidas.
Raio X
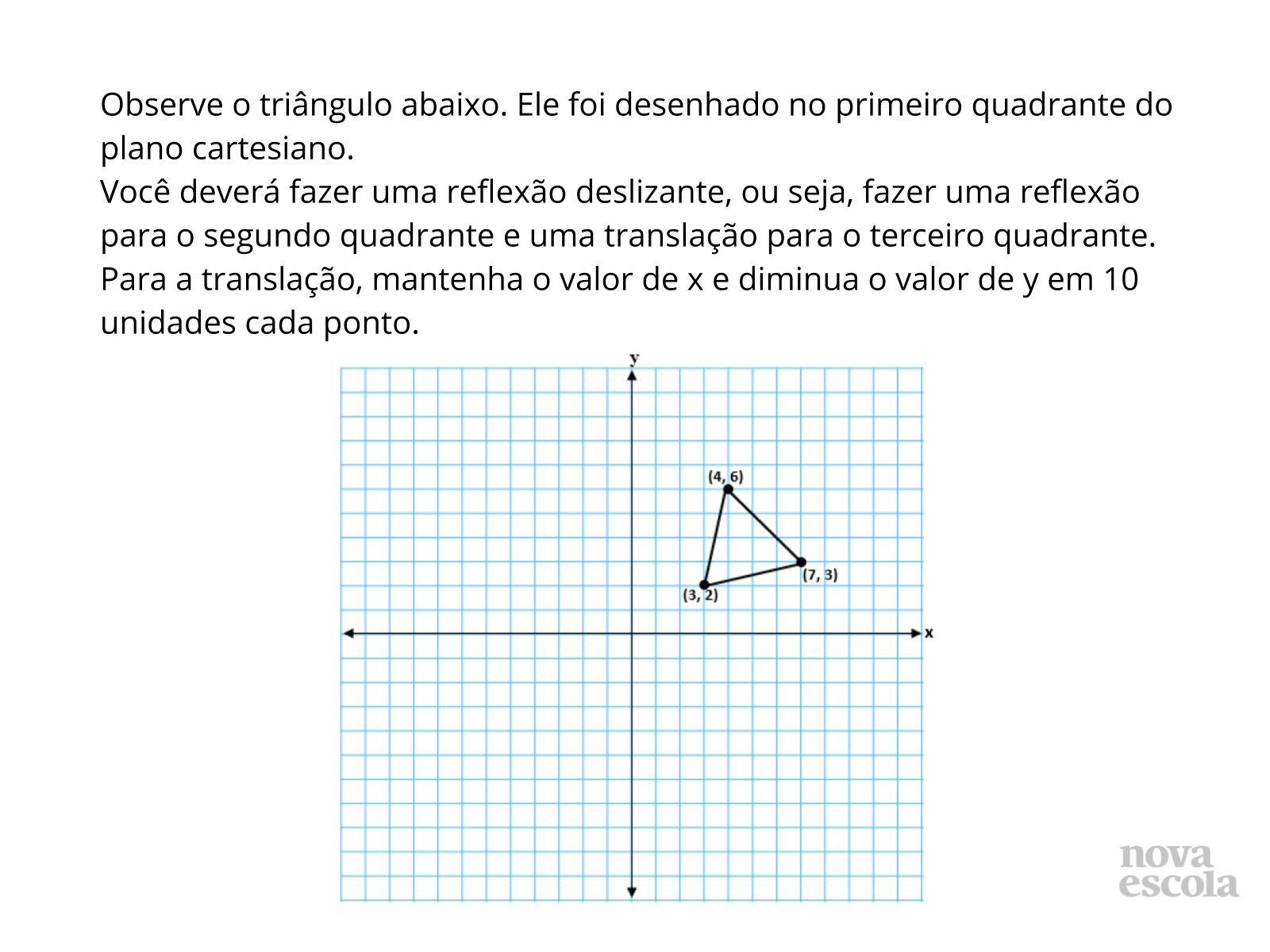
Tempo sugerido: 10 minutos.
Orientações: A atividade deverá ser realizada individualmente. Circule para verificar como os alunos estão realizando a marcação dos pontos. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando a solução na lousa.
Propósito: Verificar se os alunos aplicam corretamente a simetria de reflexão deslizante, ou seja, a junção da reflexão com a translação.
Materiais complementares para impressão:
Raio X
Resolução do raio x
Atividade complementar
Resolução da atividade complementar