Atividade Principal - Cartas
Plano de Aula
Plano de aula: Fatos fundamentais com o jogo “Truco da divisão”
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Jogos para fluência de fatos fundamentais da multiplicação e divisão
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Andresa Prata Cirino Cuginotti
Mentor: Elisa Greenhalgh Vilalta
Especialista de área: Luciana Tenuta
Habilidades da BNCC
(EF04MA03) Resolver e elaborar problemas com números naturais envolvendo adição e subtração, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
(EF04MA04) Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.
(EF04MA05) Utilizar as propriedades das operações para desenvolver estratégias de cálculo.
Objetivo específico
Adquirir fluência com os fatos fundamentais da divisão.
Conceito-chave
Fatos fundamentais da divisão, cálculo mental, propriedades da divisão, relação entre multiplicação e divisão.
Recursos necessários
Lápis, papel, cartolina ou papel cartão.
Vocabulário que será adquirido nesta aula
Divisão, relação, fluência, cálculo, estratégia.
Habilidades BNCC:
Objetivos de aprendizagem
Aula
Resumo da aula
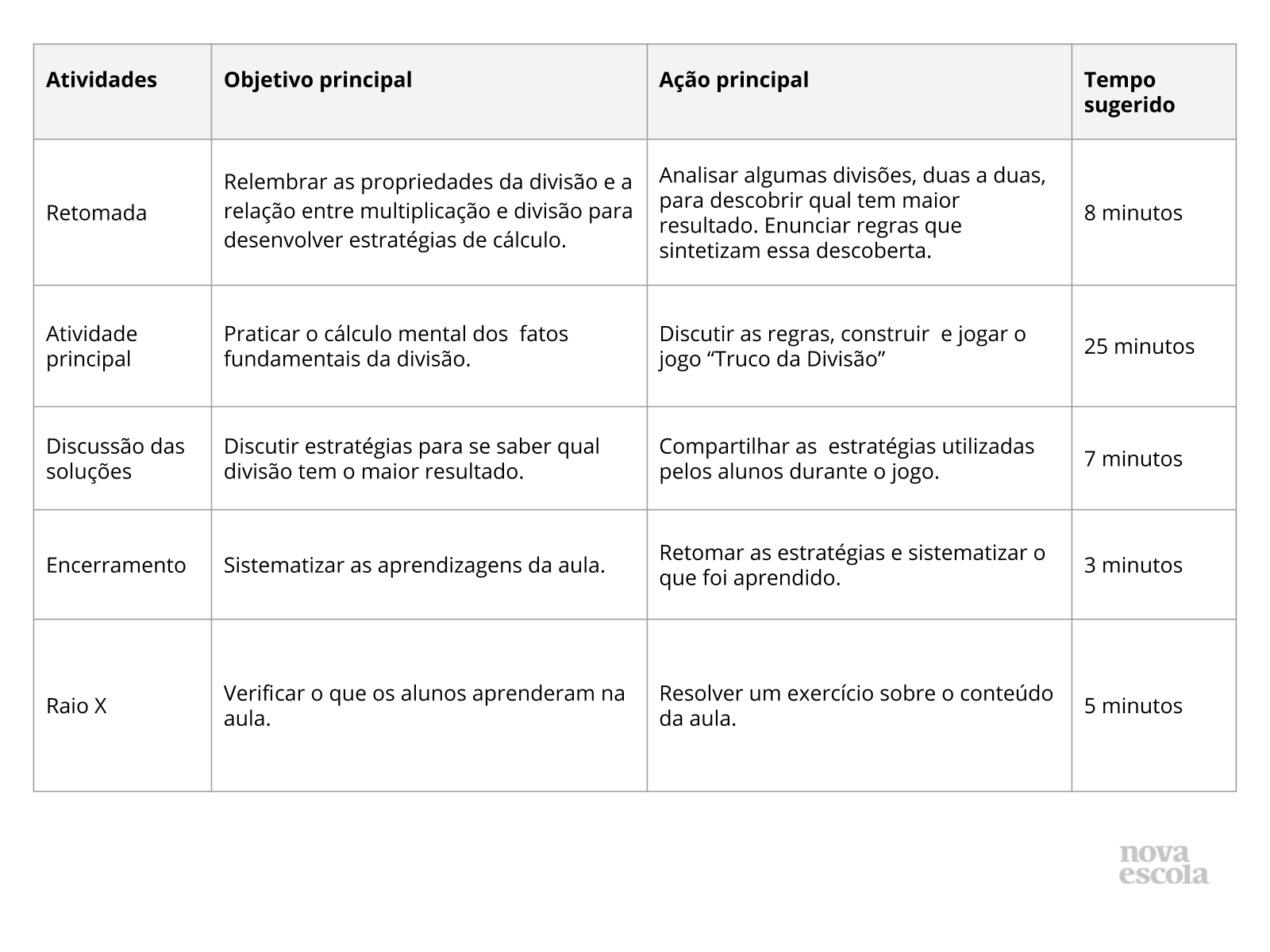Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
