Guia de intervenções
Plano de Aula
Plano de aula: Restos e múltiplos
Plano 5 de uma sequência de 5 planos. Veja todos os planos sobre Sequencia numérica recursiva formada por múltiplos
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Márcia Regina Kaminski
Mentora: Carla Simone de Albuquerque
Revisora Pedagógica: Eliane Zanin
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
(EF04MA12) Reconhecer, por meio de investigações, que há grupos de números naturais para os quais as divisões por um determinado número resultam em restos iguais, identificando regularidades.
Objetivos específicos
Identificar relações entre os múltiplos de um número natural e os restos das divisões por ele.
Conceito-chave
Sequência numérica recursiva formada por múltiplos de um número natural.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Datashow ( Opcional ).
Habilidades BNCC:
Objetivos de aprendizagem
Identificar relações entre os múltiplos de um número natural e os restos das divisões por ele.
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 5 minutos. (Slides 3, 4 e 5)
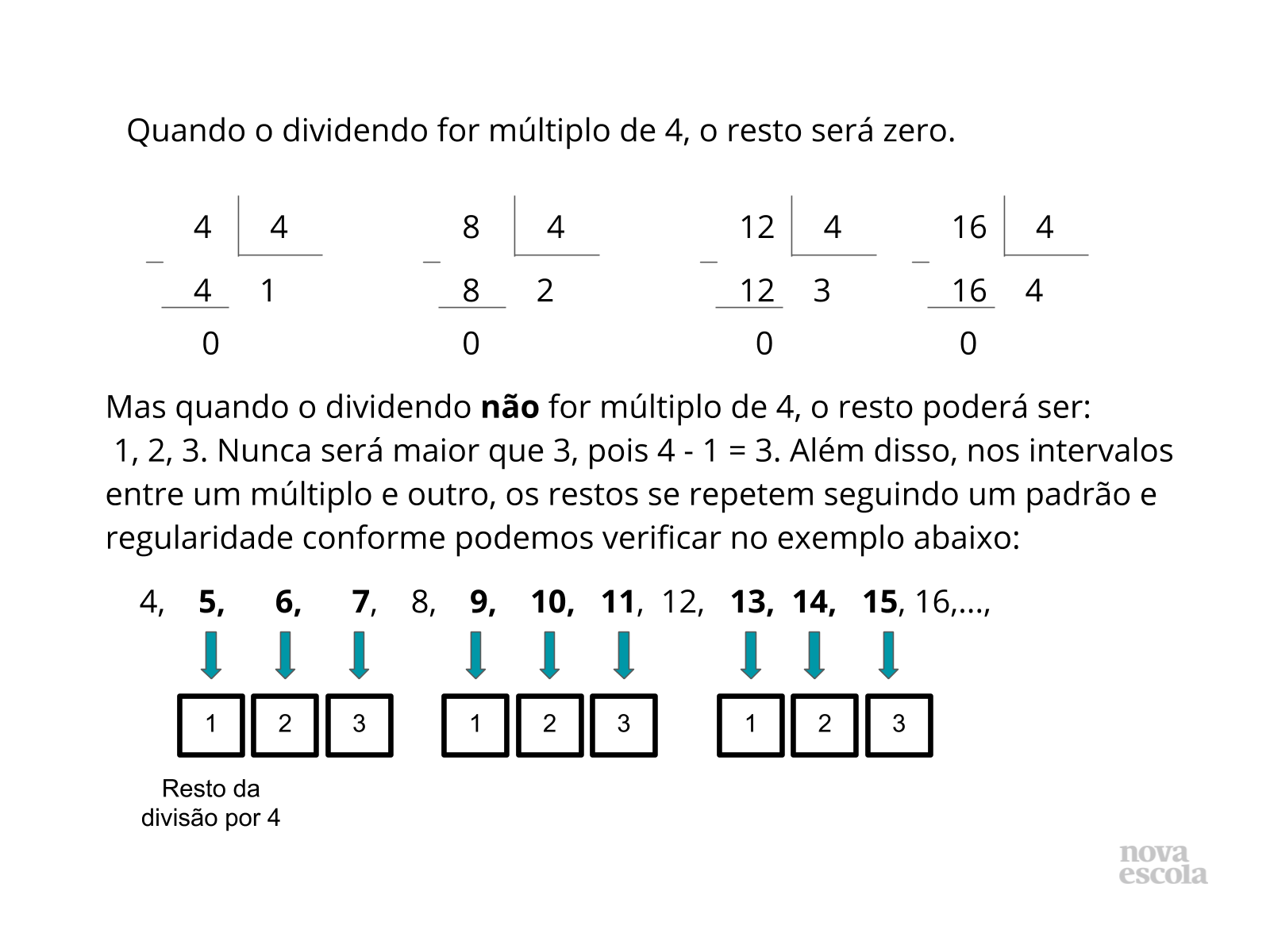
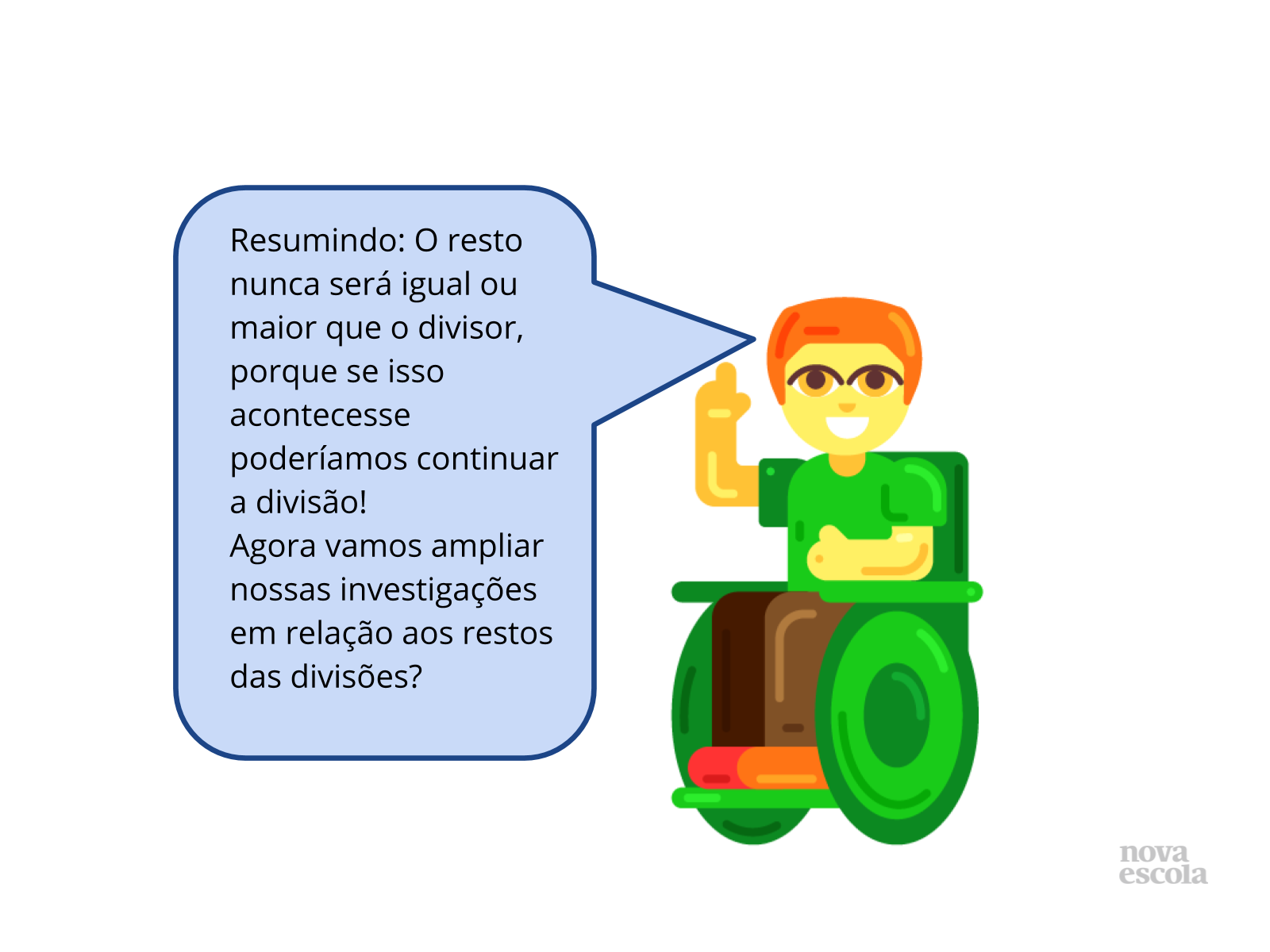
Orientação: Leia o conteúdo do balão junto com a turma, e através da discussão oral e coletiva lembre o padrão e a regularidade que podem ser encontrados nos restos das divisões de um número natural por outro. Recorde com os alunos utilizando os exemplos dos slides que o resto é zero quando o dividendo é múltiplo do divisor. Mas quando não for múltiplo, o resto será um número entre 1 e o valor do divisor menos uma unidade. Por fim, leia o conteúdo do balão do slide 5 com a turma, destacando que o resto nunca poderá ser igual ou maior que o divisor, pois se fosse, seria possível continuar a divisão. Por isso o resto sempre é menor que o divisor.
Propósito: Recordar os padrões e regularidades que existem nos restos das divisões de um número natural por outro.
Discuta com a turma:
- Vocês lembram o que aprendemos sobre os restos de uma divisão?
- Como podemos identificar os possíveis restos da divisão de um número natural por outro?
- Como essa informação pode ser útil?
- O que acontece com o resto da divisão quando o dividendo é múltiplo do divisor?
- Será que conseguimos pensar nos possíveis restos das divisões por outros números naturais?
- Que outros exemplos podemos pensar?
- Que outras relações interessantes podemos encontrar observando os restos das divisões?
Retomada
Tempo sugerido: 5 minutos. (Slides 3, 4 e 5)
Orientação: Leia o conteúdo do balão junto com a turma, e através da discussão oral e coletiva lembre o padrão e a regularidade que podem ser encontrados nos restos das divisões de um número natural por outro. Recorde com os alunos utilizando os exemplos dos slides que o resto é zero quando o dividendo é múltiplo do divisor. Mas quando não for múltiplo, o resto será um número entre 1 e o valor do divisor menos uma unidade. Por fim, leia o conteúdo do balão do slide 5 com a turma, destacando que o resto nunca poderá ser igual ou maior que o divisor, pois se fosse, seria possível continuar a divisão. Por isso o resto sempre é menor que o divisor.
Propósito: Recordar os padrões e regularidades que existem nos restos das divisões de um número natural por outro.
Discuta com a turma:
- Vocês lembram o que aprendemos sobre os restos de uma divisão?
- Como podemos identificar os possíveis restos da divisão de um número natural por outro?
- Como essa informação pode ser útil?
- O que acontece com o resto da divisão quando o dividendo é múltiplo do divisor?
- Será que conseguimos pensar nos possíveis restos das divisões por outros números naturais?
- Que outros exemplos podemos pensar?
Retomada
Tempo sugerido: 5 minutos. (Slides 3, 4 e 5)
Orientação: Leia o conteúdo do balão junto com a turma, e através da discussão oral e coletiva lembre o padrão e a regularidade que podem ser encontrados nos restos das divisões de um número natural por outro. Recorde com os alunos utilizando os exemplos dos slides que o resto é zero quando o dividendo é múltiplo do divisor. Mas quando não for múltiplo, o resto será um número entre 1 e o valor do divisor menos uma unidade. Por fim, leia o conteúdo do balão do slide 5 com a turma, destacando que o resto nunca poderá ser igual ou maior que o divisor, pois se fosse, seria possível continuar a divisão. Por isso o resto sempre é menor que o divisor.
Propósito: Recordar os padrões e regularidades que existem nos restos das divisões de um número natural por outro.
Discuta com a turma:
- Vocês lembram o que aprendemos sobre os restos de uma divisão?
- Como podemos identificar os possíveis restos da divisão de um número natural por outro?
- Como essa informação pode ser útil?
- O que acontece com o resto da divisão quando o dividendo é múltiplo do divisor?
- Será que conseguimos pensar nos possíveis restos das divisões por outros números naturais?
- Que outros exemplos podemos pensar?
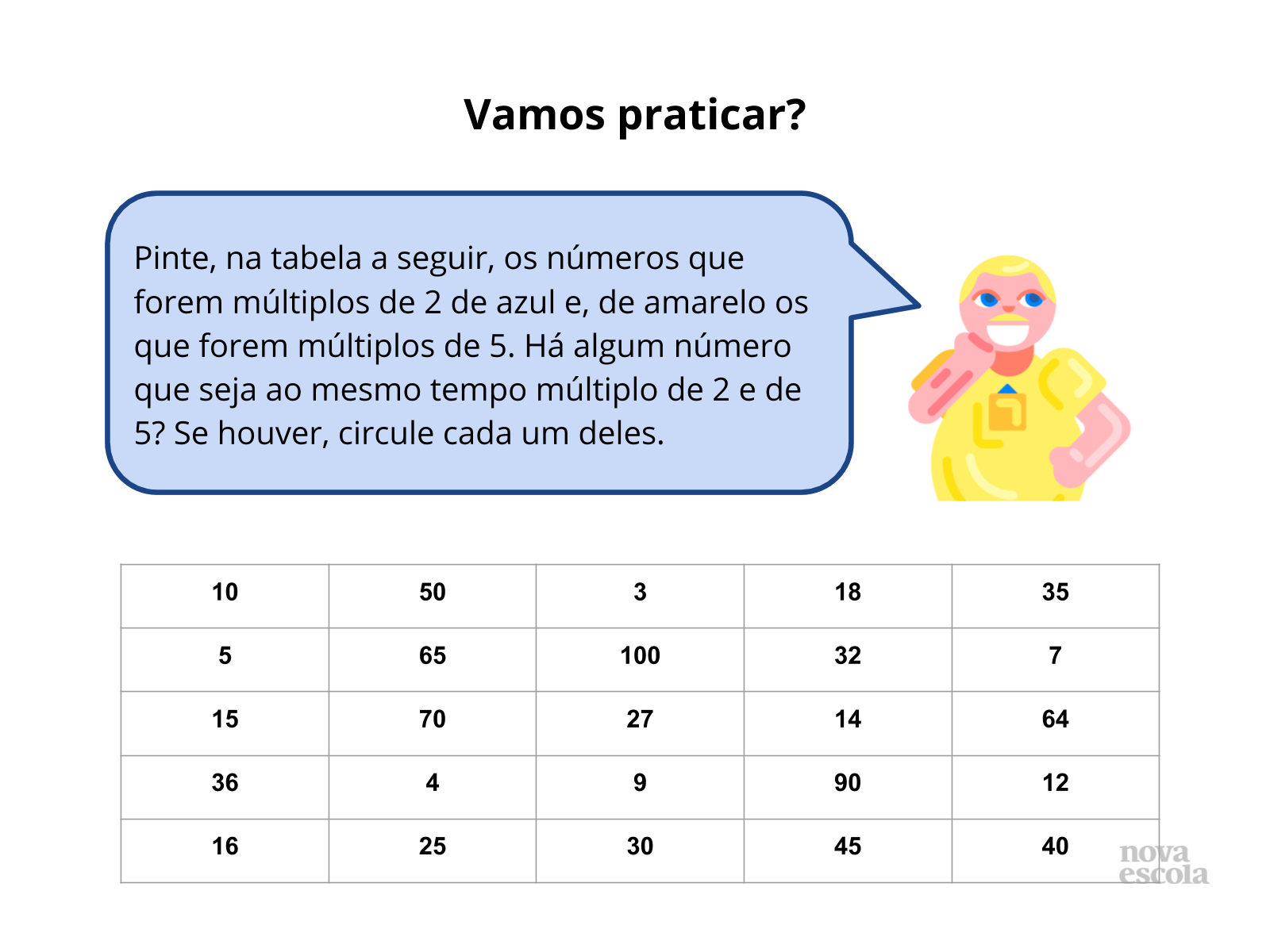
Atividade principal
Tempo sugerido: 15 minutos.
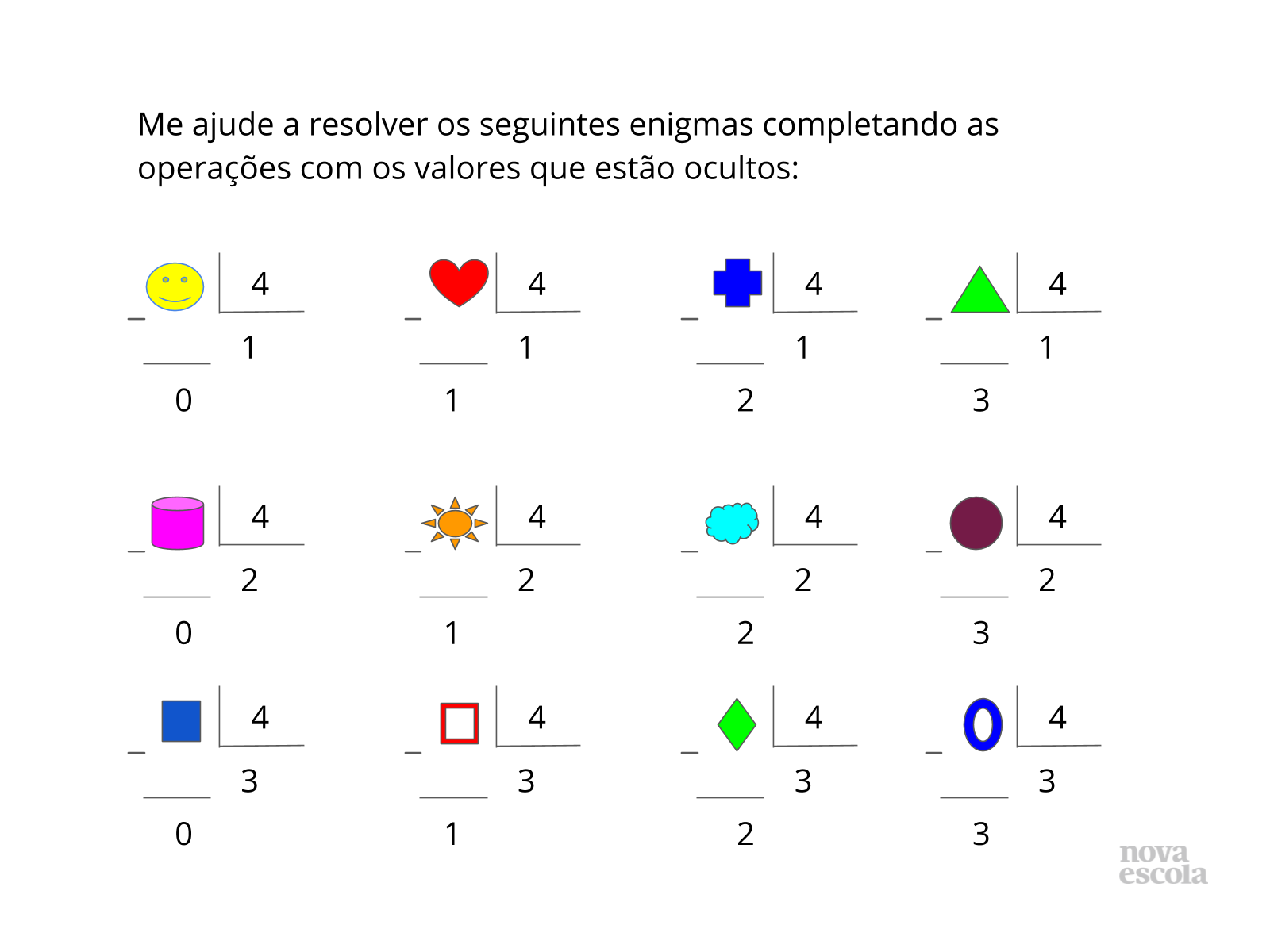
Orientação: Organize os alunos em duplas de trabalho e peça que tentem resolver os enigmas, identificando os números que estão ocultos.
Propósito: Identificar as relações presentes entre a sequência de múltiplos de um número natural e os restos das divisões dos números naturais por ele.
Discuta com a turma:
- Como podemos identificar os números ocultos?
- Como vocês estão pensando?
- Que estratégias podemos utilizar?
Materiais complementares para impressão:
Discussão das soluções

Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
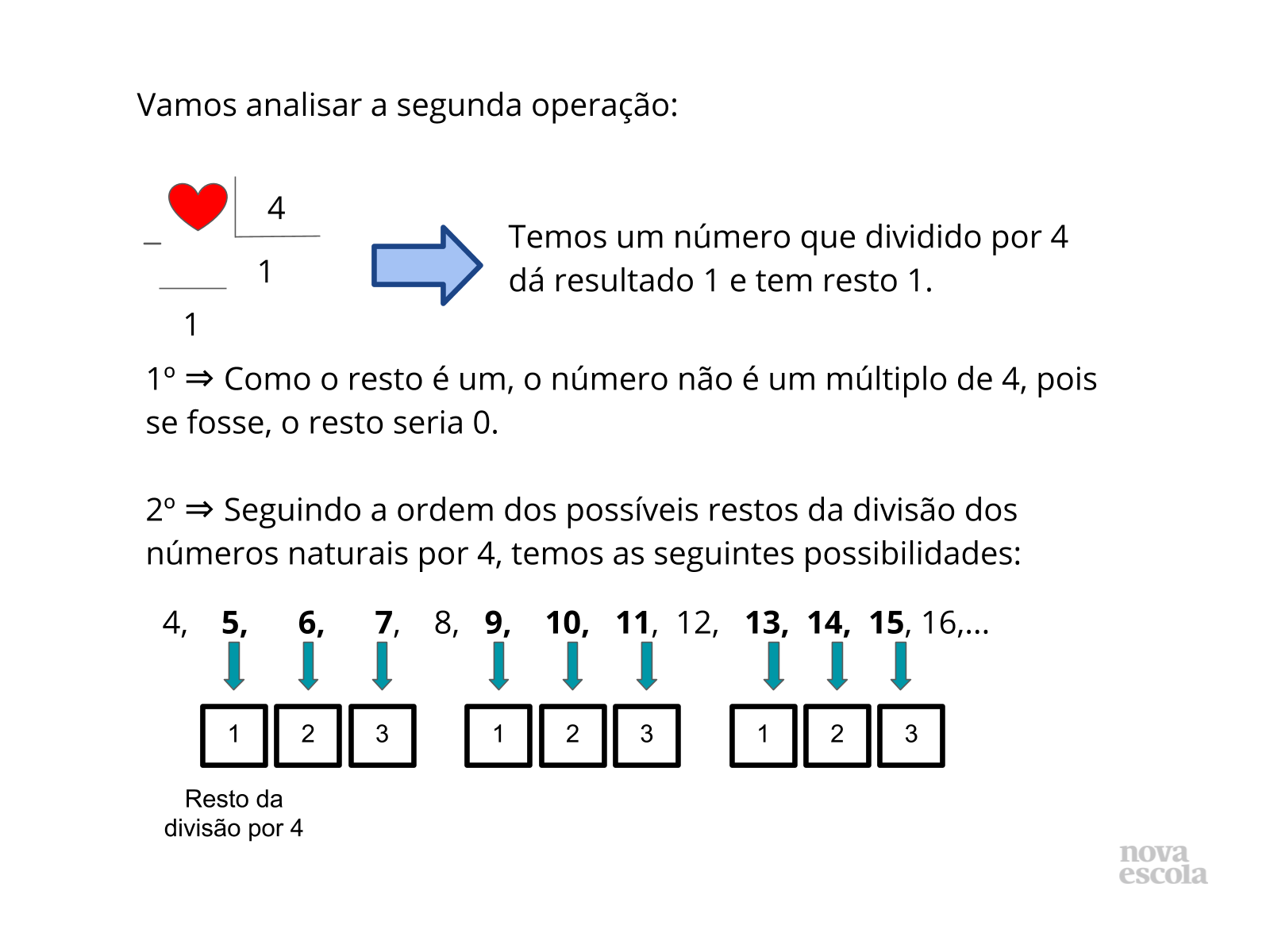
Orientação: Pergunte aos alunos como as duplas pensaram para resolver os enigmas. Que raciocínio utilizaram? Peça que as duplas comentem oral e coletivamente que estratégias empregaram para identificar os números ocultos. Caso haja algum raciocínio equivocado, discuta com a turma onde está o possível erro. Depois apresente as possibilidades de solução dos slides 7 a 10 e verifique se algumas duplas utilizaram esta mesma forma de solução.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- Como vocês pensaram para resolver os enigmas?
- Conhecer os restos das divisões em cada caso foi importante para chegar à solução? De que forma?
Material Complementar:
Discussão das soluções

Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
Orientação: Pergunte aos alunos como as duplas pensaram para resolver os enigmas. Que raciocínio utilizaram? Peça que as duplas comentem oral e coletivamente que estratégias empregaram para identificar os números ocultos. Caso haja algum raciocínio equivocado, discuta com a turma onde está o possível erro. Depois apresente as possibilidades de solução dos slides 7 a 10 e verifique se algumas duplas utilizaram esta mesma forma de solução.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- Como vocês pensaram para resolver os enigmas?
- Conhecer os restos das divisões em cada caso foi importante para chegar à solução? De que forma?
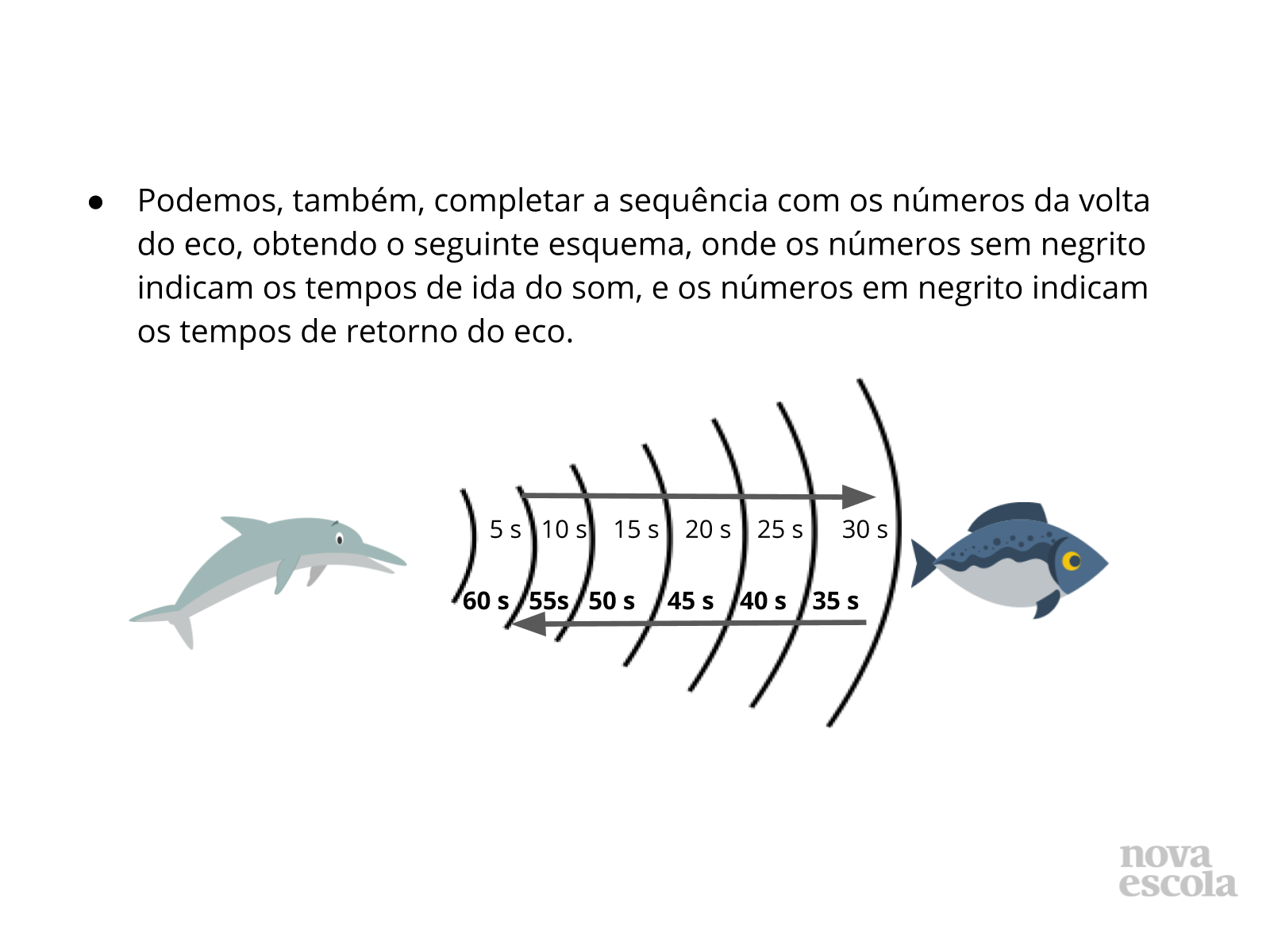
Discussão das soluções
Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
Orientação: Pergunte aos alunos como as duplas pensaram para resolver os enigmas. Que raciocínio utilizaram? Peça que as duplas comentem oral e coletivamente que estratégias empregaram para identificar os números ocultos. Caso haja algum raciocínio equivocado, discuta com a turma onde está o possível erro. Depois apresente as possibilidades de solução dos slides 7 a 10 e verifique se algumas duplas utilizaram esta mesma forma de solução.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- Como vocês pensaram para resolver os enigmas?
- Conhecer os restos das divisões em cada caso foi importante para chegar à solução? De que forma?
Discussão das soluções
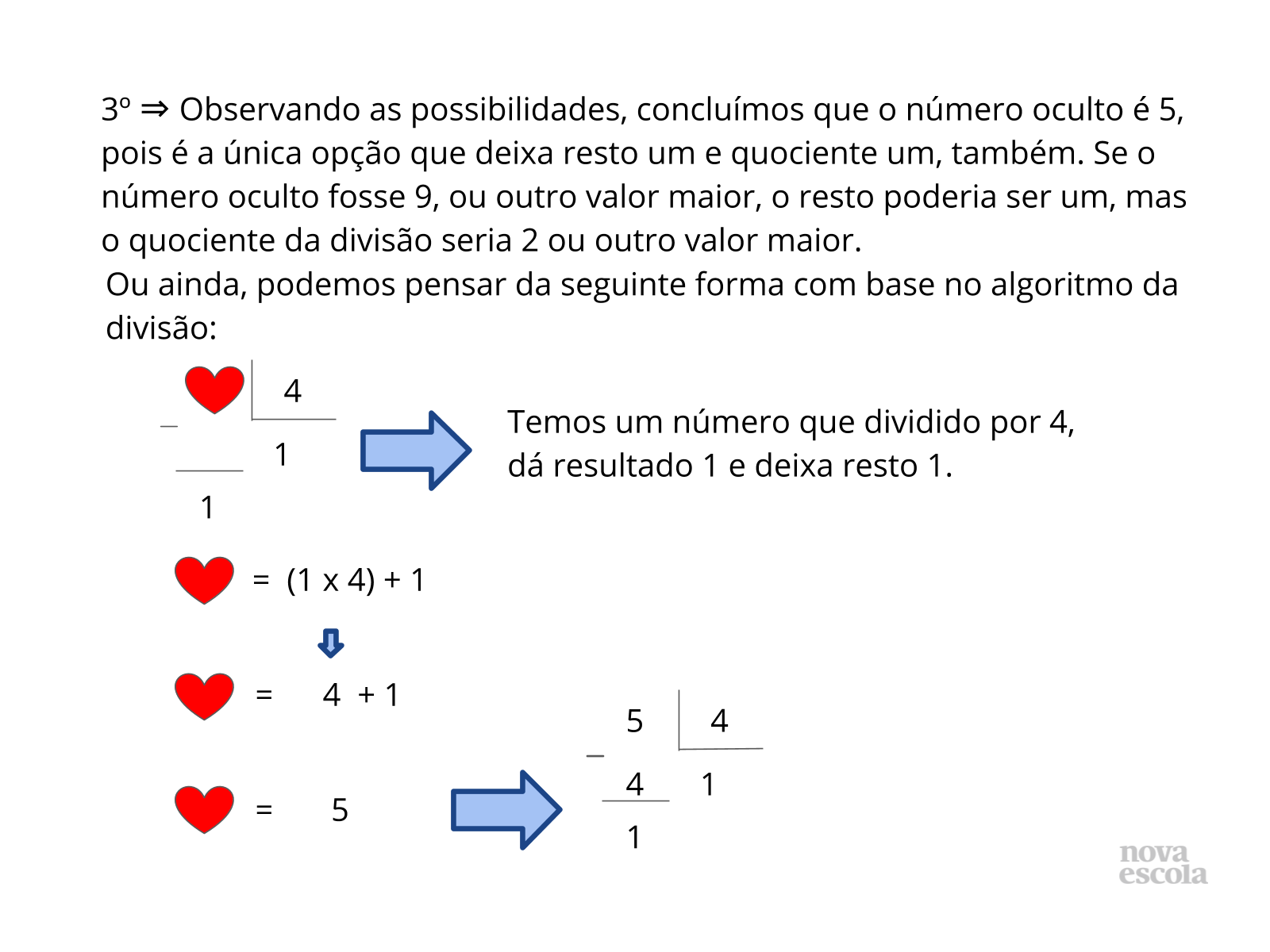
Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
Orientação: Pergunte aos alunos como as duplas pensaram para resolver os enigmas. Que raciocínio utilizaram? Peça que as duplas comentem oral e coletivamente que estratégias empregaram para identificar os números ocultos. Caso haja algum raciocínio equivocado, discuta com a turma onde está o possível erro. Depois apresente as possibilidades de solução dos slides 7 a 10 e verifique se algumas duplas utilizaram esta mesma forma de solução.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- Como vocês pensaram para resolver os enigmas?
- Conhecer os restos das divisões em cada caso foi importante para chegar à solução? De que forma?
Discussão das soluções

Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
Orientação: Leia o conteúdo do balão com os alunos e passe para a apresentação dos resultados de todos os enigmas conforme apresentados nos slides 12 a 14.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- Vamos verificar se todos encontramos os mesmos resultados?
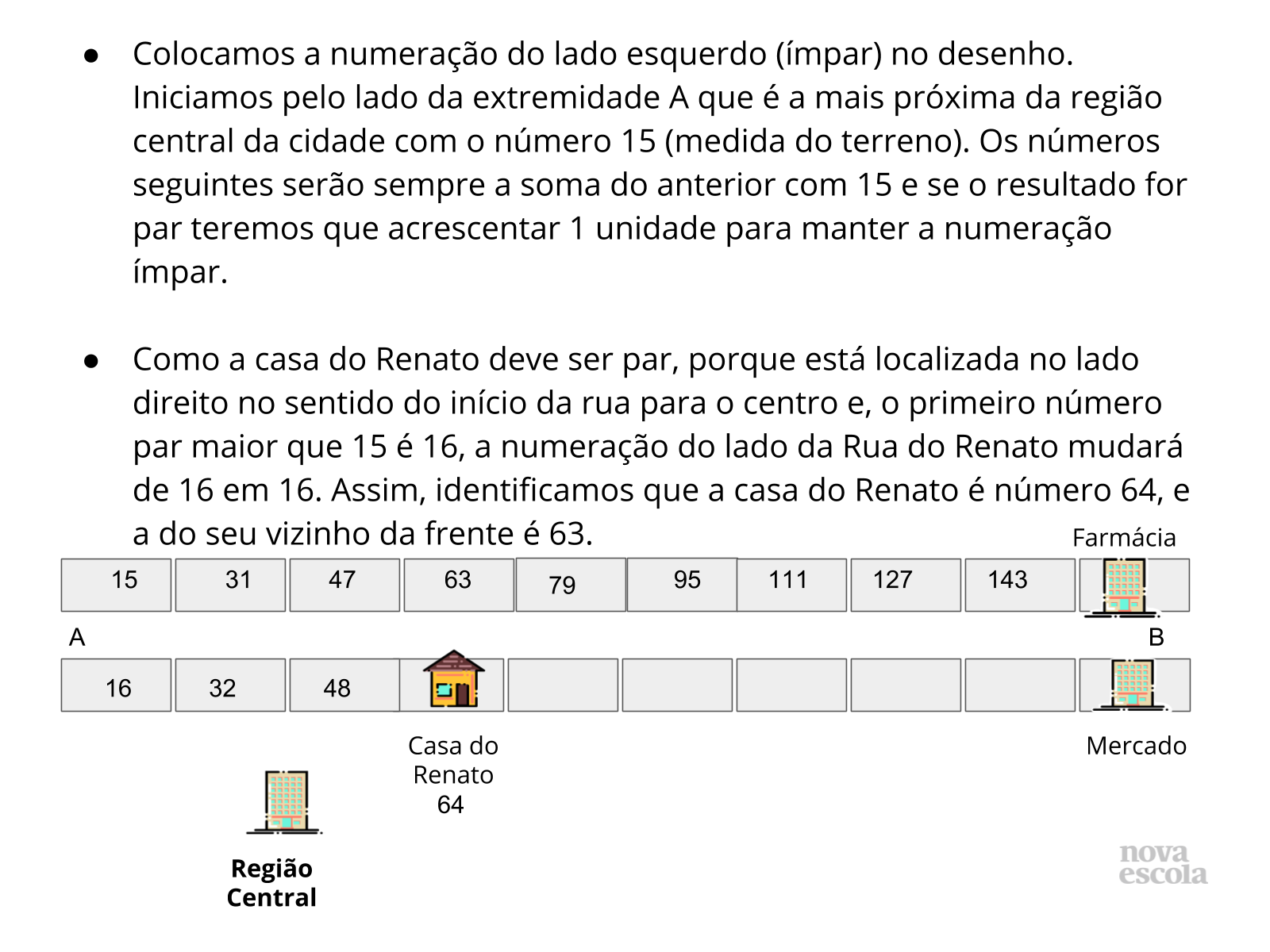
Discussão das soluções
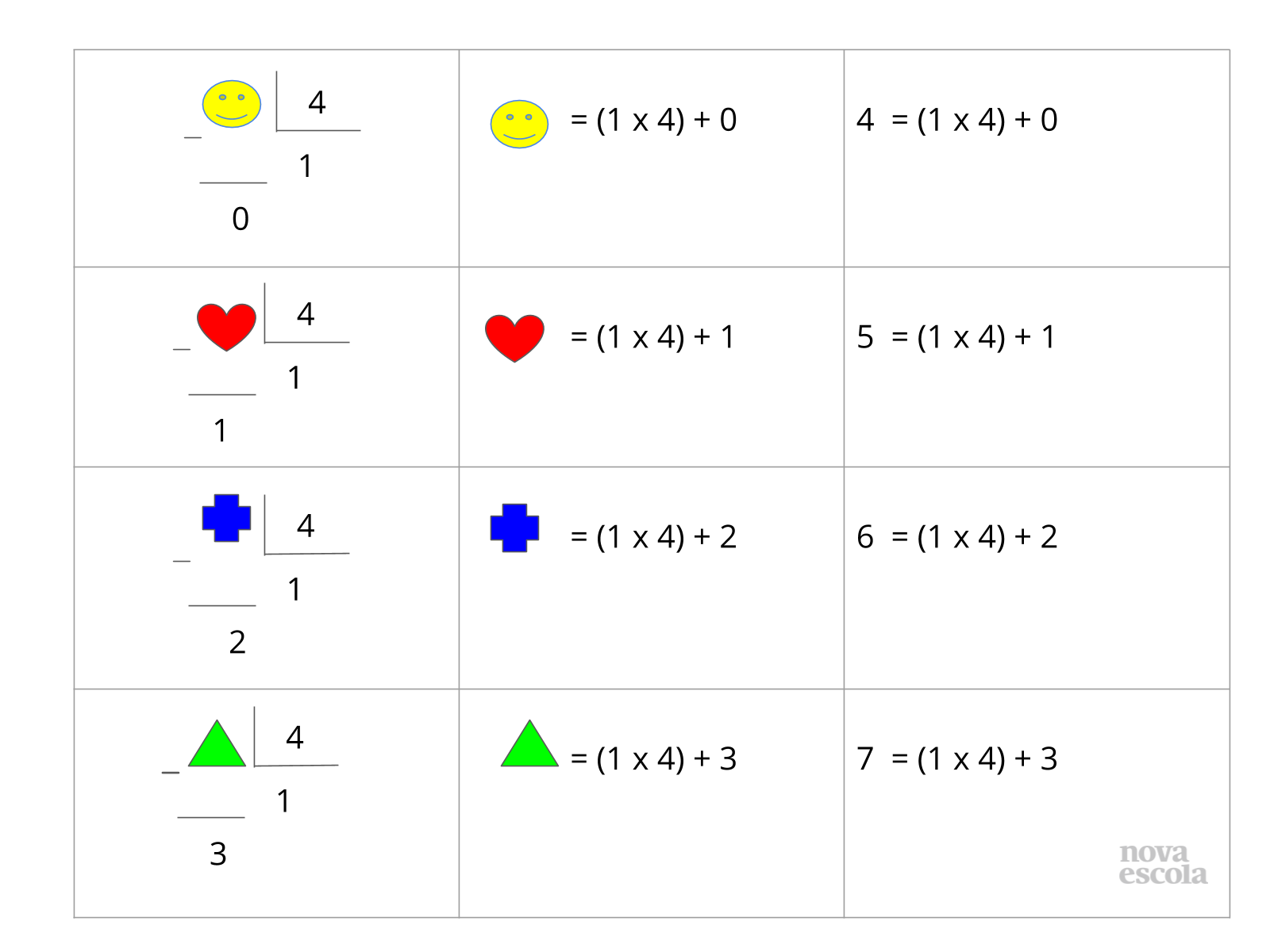
Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
Orientação: Apresente os quadros dos slides 12 a 14 para os alunos, destacando em cada caso o resultado obtido para o valor oculto. Chame a atenção para a última coluna, destacando a relação presente entre os múltiplos de 4, que são obtidos através da multiplicação dos números naturais por 4 e os possíveis restos das divisões por 4.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- O que podemos observar nos resultados obtidos?
- Há alguma relação com os possíveis restos das divisões por 4?
- Há alguma relação com os múltiplos de 4?
Discussão das soluções

Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
Orientação: Apresente os quadros dos slides 12 a 14 para os alunos, destacando em cada caso o resultado obtido para o valor oculto. Chame a atenção para a última coluna, destacando a relação presente entre os múltiplos de 4, que são obtidos através da multiplicação dos números naturais por 4 e os possíveis restos das divisões por 4.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- O que podemos observar nos resultados obtidos?
- Há alguma relação com os possíveis restos das divisões por 4?
- Há alguma relação com os múltiplos de 4?
Discussão das soluções

Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
Orientação: Apresente os quadros dos slides 12 a 14 para os alunos, destacando em cada caso o resultado obtido para o valor oculto. Chame a atenção para a última coluna, destacando a relação presente entre os múltiplos de 4, que são obtidos através da multiplicação dos números naturais por 4 e os possíveis restos das divisões por 4.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- O que podemos observar nos resultados obtidos?
- Há alguma relação com os possíveis restos das divisões por 4?
- Há alguma relação com os múltiplos de 4?
Discussão das soluções
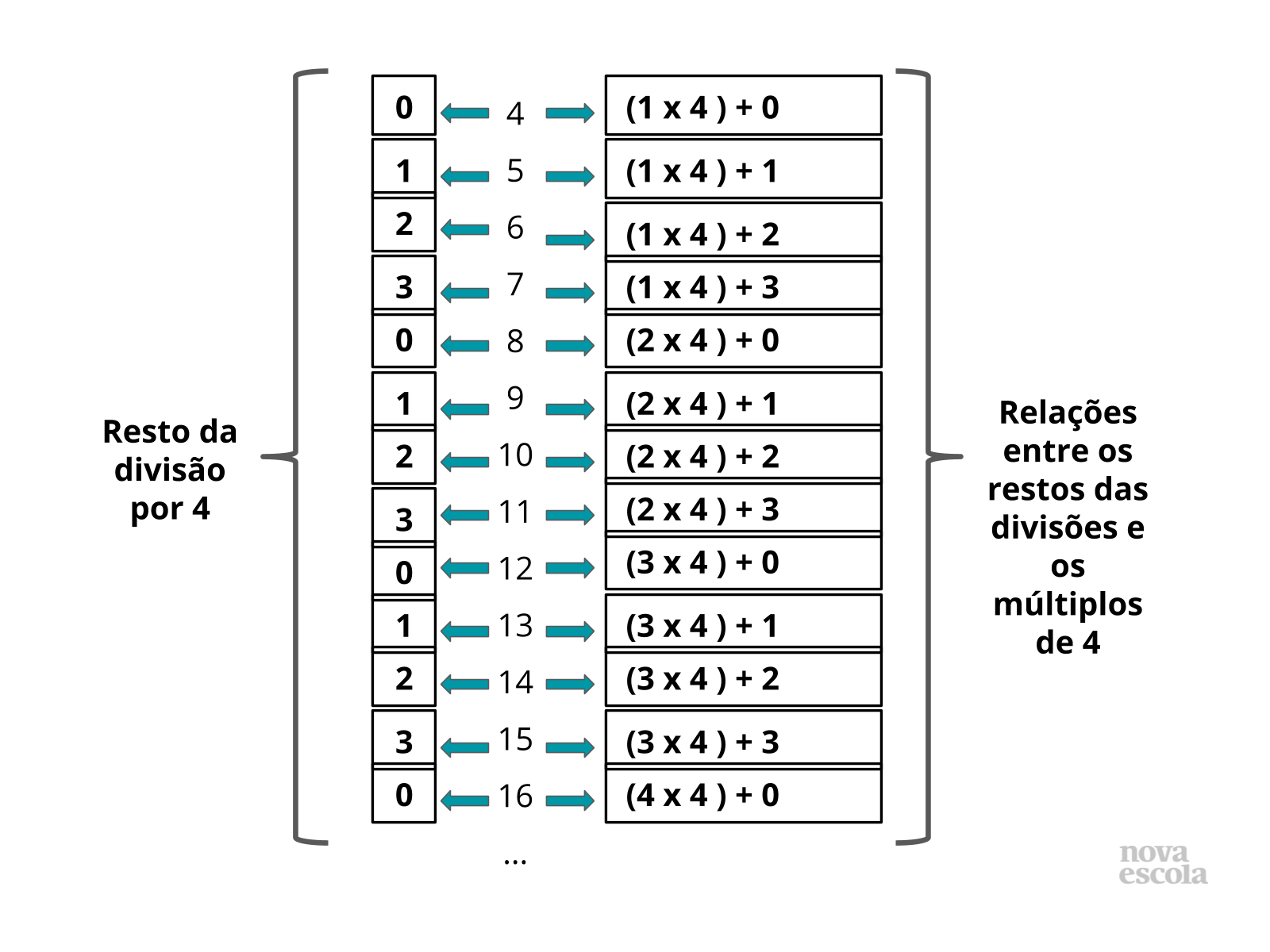
Tempo sugerido: 15 minutos. (Slides 7, 8, 9, 10, 11, 12, 13, 14 e 15)
Orientação: Apresente o esquema deste slide, destacando que podemos relacionar os números naturais com uma operação de adição dos múltiplos de 4 com os possíveis restos das divisões por 4. Saliente que isso acontece para outros divisores também.
Propósito: Destacar as relações presentes entre os múltiplos de um número natural e os restos possíveis das divisões por ele.
Discuta com a turma:
- Como ficaria este esquema para outros divisores?
- Que outros exemplos podemos apresentar? Deixe que a turma comente outros exemplos e anote alguns na lousa para que todos observem.
Encerramento

Orientações: Leia o conteúdo do balão com os alunos para enfatizar o que foi estudado durante a aula.
Propósito: Finalizar a aula resumindo o que foi estudado sobre as relações entre os múltiplos de um número e os possíveis restos das divisões por ele.
Discuta com a turma:
- Será que esta informação pode nos ajudar a resolver problemas? Como?
Raio x
Orientações: Peça que, individualmente, os alunos leiam a atividade e tentam resolver os enigmas com base no que foi estudado. Reserve 2 minutos para a correção coletiva e oral com a turma.
Propósito: Aplicar os conhecimentos aprendidos durante a aula para resolver problemas.
Discuta com a turma:
- Todos encontraram as mesmas respostas? Anote no quadro todas ou algumas das respostas obtidas em cada questão, inclusive algumas que apresentem erros, para que possam ser discutidos.
- Como vocês pensaram? Discuta com os alunos as diferentes formas utilizadas para a resolução.
Materiais complementares para impressão:
Sugestão de adaptação para ensino remoto
Código do plano
MAT4_14ALG_05
Recursos
USAR APENAS FERRAMENTAS EM PORTUGUÊS E GRATUITAS
- Necessários: (apenas se forem absolutamente indispensáveis; caso contrário, inserir todos como opcionais)
- Opcionais: Google Documentos, Google Apresentações.
Para este plano, foque na etapa Atividade Principal.
Retomada
Proponha aos alunos que criem uma sequência de números naturais a partir do número 5 e peça que registrem o resto da divisão de cada um desses números em uma nova sequência. Você pode indicar o uso de uma tabela inserida em arquivo do Google Documentos como o modelo a seguir, porém ofertada em branco, sem os valores aqui presentes para sua conferência:

Isso também pode ser feito em folha impressa, mas em ambas situações precisaremos pensar em propor questões que levem os alunos a refletirem sobre suas ações, visto que eles estão trabalhando remota e individualmente.
Atividade principal
Proponha a atividade em arquivo via Google Apresentações solicitando que cada aluno crie uma cópia do arquivo compartilhado para fazer sua resolução. Você pode inserir as questões presentes nas orientações ao professor em um dos slides do arquivo (e incluir quantas mais achar necessárias para que a turma possa trabalhar individualmente). É importante que isso seja feito a partir de questões problematizadoras, sem dar pistas e dizer o que fazer, mas levando a turma a refletir sobre as ações possíveis.
Caso os alunos não tenham acesso à internet você pode fazer o mesmo movimento em folhas impressas, desde que a devolutiva seja realizada com sucesso. No caso do arquivo digital essa devolutiva pode ser feita a partir de comentários nas resoluções.
Discussão das soluções
Usando o mesmo recurso do Google Apresentações como na etapa anterior (Atividade Principal), é possível criar uma sequência de slides com respostas diferentes, tanto corretas quanto incorretas, solicitando que a turma responda às questões sobre elas, fazendo comparações, etc. Essas questões podem ser respondidas via Google Documentos ou ainda usando o próprio Google Apresentações. Lembre-se de inserir as tabelas conforme os slides 11, 12 e 13, para servirem de exemplo para os alunos compreenderem o processo operatório.
Assim como na etapa anterior o aluno pode responder em folha impressa também.
Sistematização
Não há.
Encerramento
Proponha que os alunos criem uma lista dos itens mais importantes da aula no próprio caderno.
Raio X
Peça que a turma responda às questões propostas nesta etapa usando o Google Documentos, criando uma cópia do arquivo e disponibilizando para o professor o link da resolução, contendo também uma breve explicação.
Caso não tenham acesso à internet é possível fazer isso em folha impressa.
Convite às famílias
Convide a família a acompanhar a etapa de Discussão das soluções, para que os alunos tenham um suporte de diálogo sobre as resoluções, trocando ideias e perguntando sobre os processos de divisão utilizados.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Márcia Regina Kaminski
Mentora: Carla Simone de Albuquerque
Revisora Pedagógica: Eliane Zanin
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
(EF04MA12) Reconhecer, por meio de investigações, que há grupos de números naturais para os quais as divisões por um determinado número resultam em restos iguais, identificando regularidades.
Objetivos específicos
Identificar relações entre os múltiplos de um número natural e os restos das divisões por ele.
Conceito-chave
Sequência numérica recursiva formada por múltiplos de um número natural.
Recursos necessários
- Folha de papel A4 branca;
- Atividades impressas em folhas, coladas no caderno ou não;
- Datashow ( Opcional ).