Resumo da aula
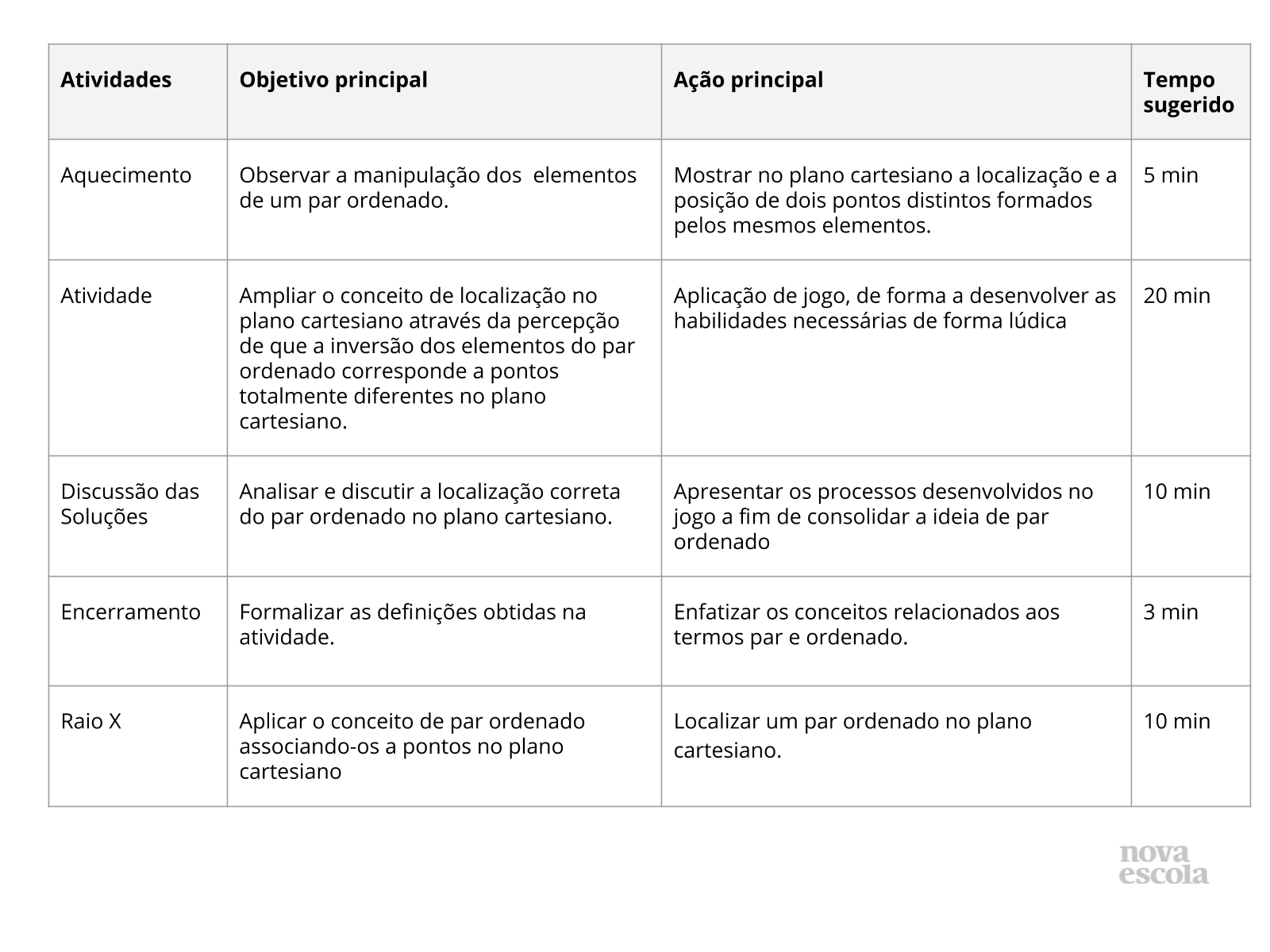
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo.

Tempo sugerido: 2 minutos.
Propósito: Apresentar os objetivos da aula.
Orientações: Apresente o objetivo da aula aos seus alunos.
Aquecimento.

Tempo sugerido: 5 minutos.
Propósito: Observar a manipulação dos elementos de um par ordenado.
Orientações: Peça aos alunos que observem os valores obtidos no dado da imagem. Incentive os alunos a responderem às perguntas do slide e utilize o plano cartesiano para debater as respostas dos alunos referentes a posição dos pontos citados. Espera-se que os alunos percebam a possibilidade de montar dois pares ordenados com os números 3 e 6: (6,3) e (3,6).
Discuta com a turma:
- Quantas informações são necessárias para determinar a localização desse par no plano cartesiano?
- Podemos nos referir a essa localização como um ponto, mesmo sendo necessário duas informações.
- Como representar esse ponto?
Materiais complementares:
Atividade aquecimento
Resolução da atividade aquecimento
Aquecimento.
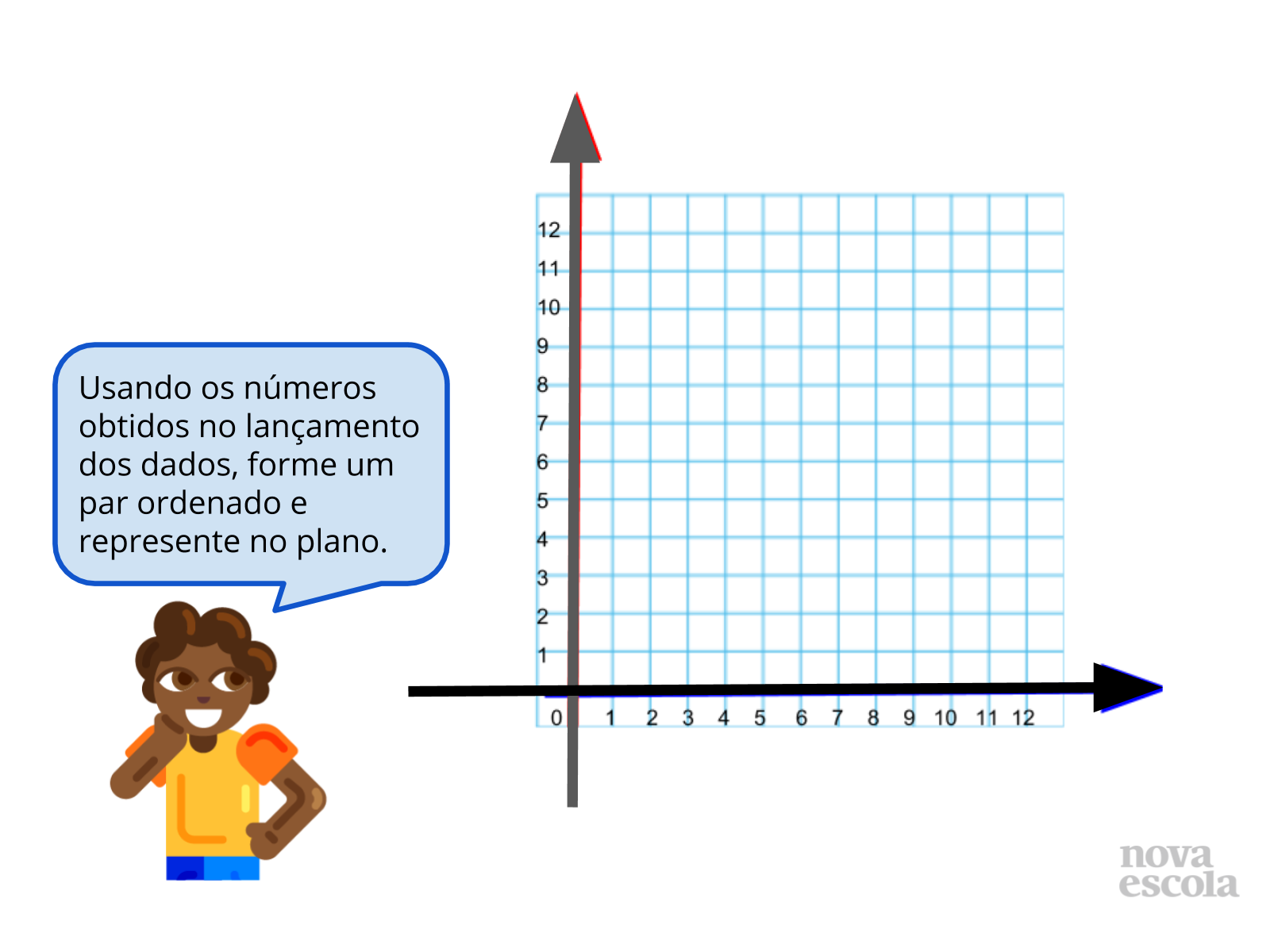
Tempo sugerido: 5 minutos.
Propósito: Observar a manipulação dos elementos de um par ordenado.
Orientações: Peça aos alunos que observem os valores obtidos no dado da imagem. Incentive os alunos a responderem às perguntas do slide e utilize o plano cartesiano para debater as respostas dos alunos referentes a posição dos pontos citados. Espera-se que os alunos percebam a possibilidade de montar dois pares ordenados com os números 3 e 6: (6,3) e (3,6).
Discuta com a turma:
- Quantas informações são necessárias para determinar a localização desse par no plano cartesiano?
- Podemos nos referir a essa localização como um ponto, mesmo sendo necessário duas informações.
- Como representar esse ponto?
Atividade Principal - Jogo de Tabuleiro
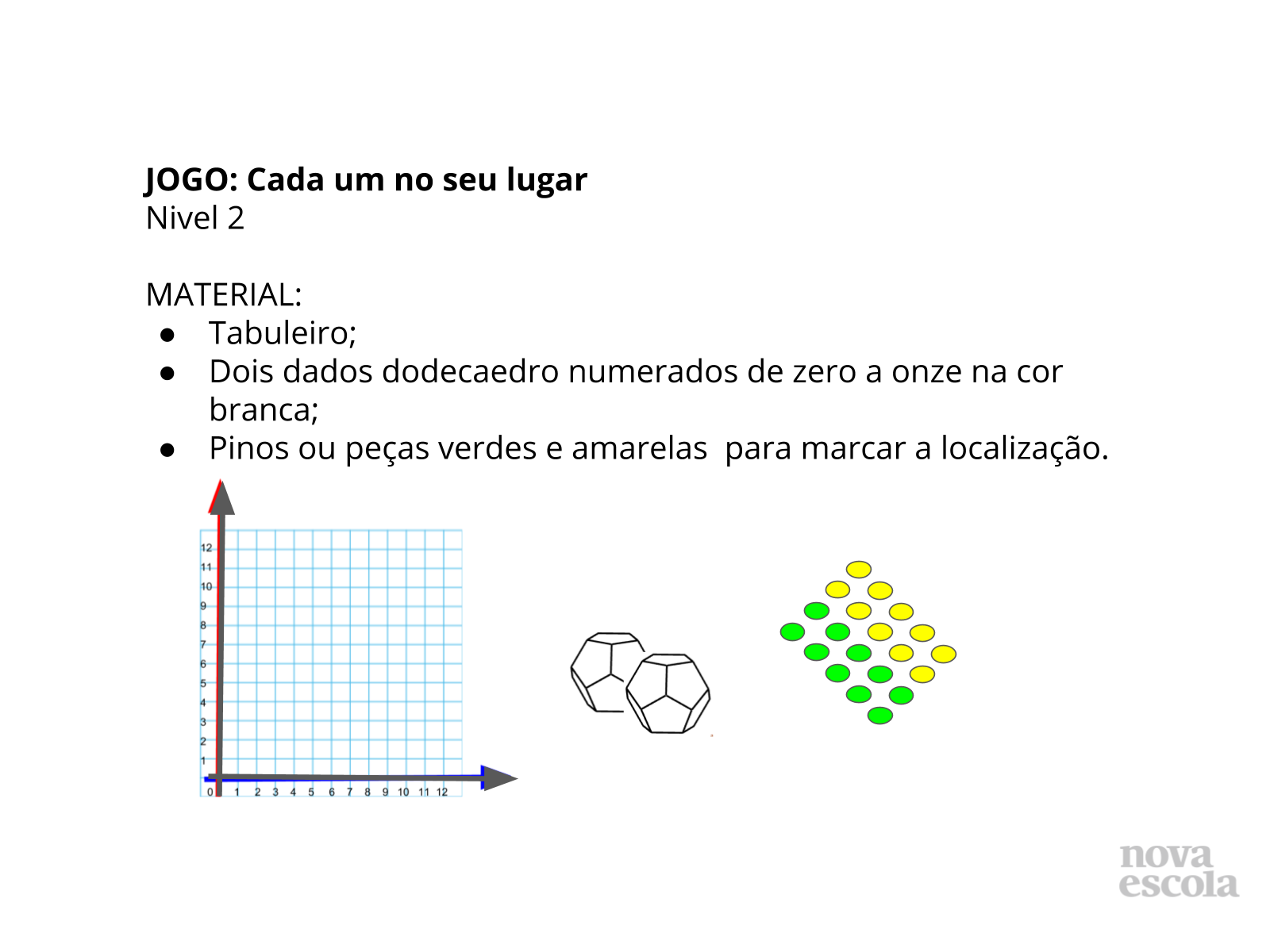
Tempo sugerido: 20 minutos.
Propósito: Ampliar o conceito de localização de pontos no plano cartesiano e observar que a ordem dos elementos (x, y) altera a posição ponto no plano e portanto o par ordenado obtido dessa troca representa um ponto diferente.
ORIENTAÇÕES: Este jogo é uma oportunidade dos alunos começarem a montar os pares ordenados e criar estratégias para eliminar os pinos do adversário. A ideia de deixar que os alunos escolham a ordem dos números no par ordenado fará com que utilizem com autonomia a convenção matemática e o conceito de par ordenado. Acompanhe com atenção essa atividade e verifique se o par ordenado escolhido marcado na tabela coincide com a anotação no tabuleiro. Verifique se os alunos compreenderam que o primeiro número se refere a um deslocamento no eixo das abscissas. Analogamente, veja se entenderam o deslocamento a ser feito com o segundo número do par. O professor poderá encontrar a atividade para impressão, juntamente com os objetivos, regras e materiais necessários. Nesta atividade os alunos também terão uma tabela para preencher com os pares obtidos por eles a cada jogada e um plano similar ao tabuleiro para que o professor possa acompanhar e associar valor obtido e marcação no plano a fim de garantir o andamento correto da atividade. Mantenha a turma dividida em grupos de 4 alunos onde haverá duas duplas adversárias, para que juntos desenvolvam boas estratégias.
Discuta com a turma:
- A mudança de ordem dos pares ordenados nesta atividade altera a localização no plano?
- Em que a autonomia de escolher a ordem do par ordenado influência em sua estratégia?
Materiais complementares:
Atividade principal
Resolução da atividade principal
Guia de intervenção
Discussão das Soluções.
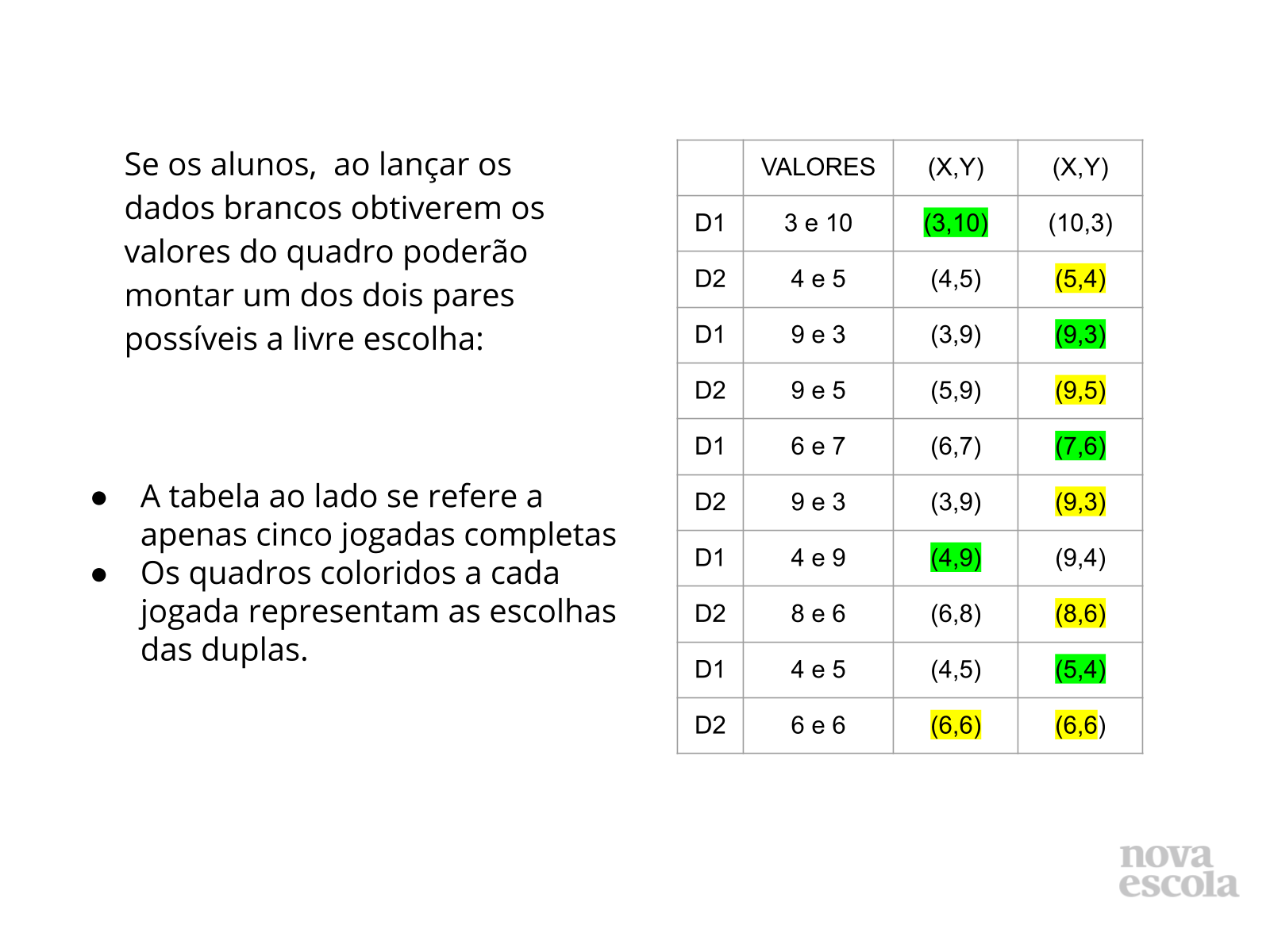
Tempo sugerido: 10 minutos (slides 5 e 6).
Propósito: Analisar e discutir a localização correta do par ordenado no plano cartesiano.
Orientação: Na rodada 2, os jogadores têm a chance de aprimorar sua estratégia, uma vez que poderão escolher o par ordenado mais conveniente para eliminar peças do adversário. No jogo acima, o alunos da dupla amarela acabaram de obter vantagem de um pino com relação à dupla vermelha.
Discuta com a turma:
- Esse formato de jogo permite ampliar as estratégias?
- Como?
Discussão das Soluções.
Tempo sugerido: 10 minutos (slides 5 e 6).
Propósito: Analisar e discutir a localização correta do par ordenado no plano cartesiano.
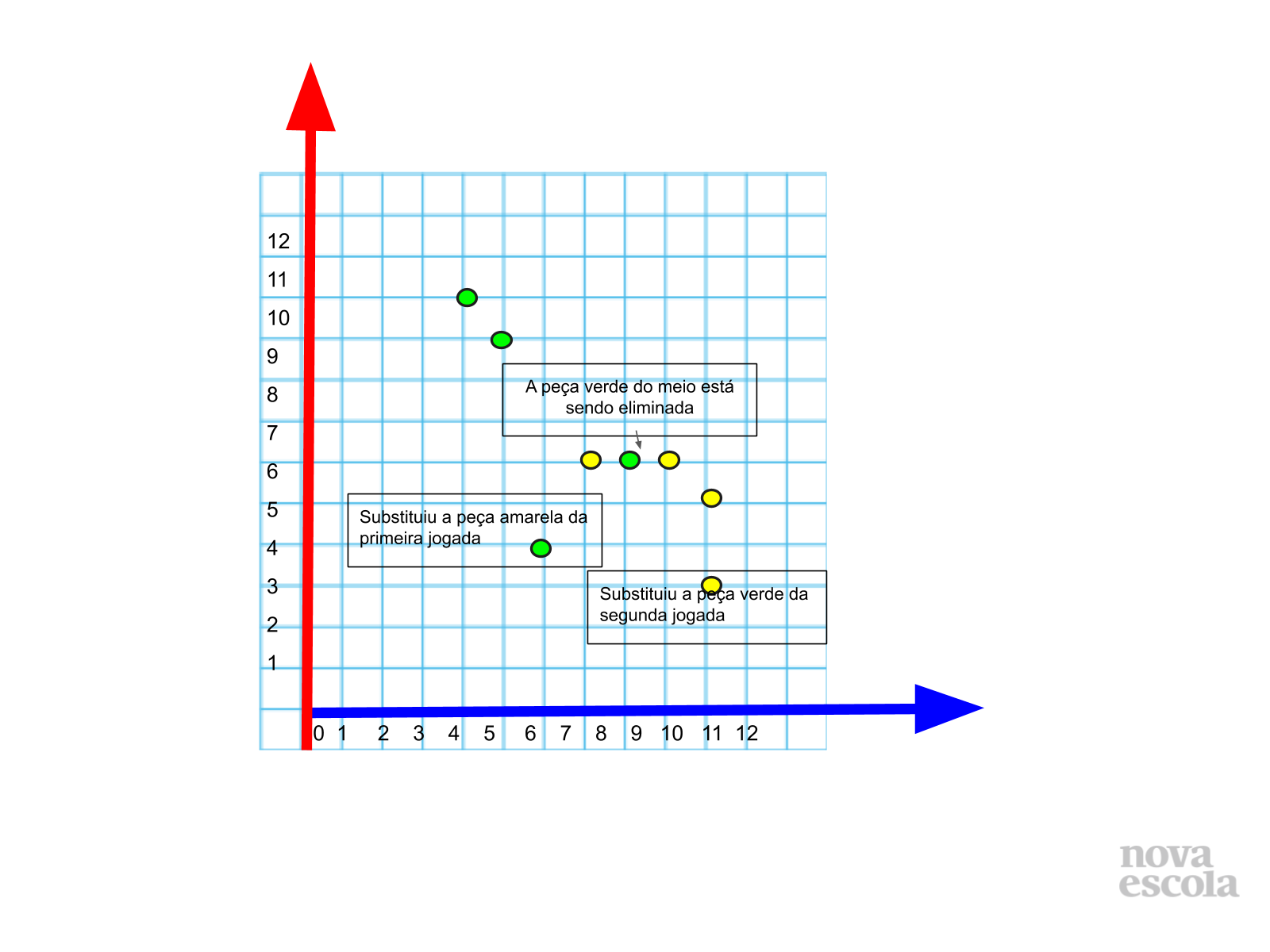
Orientação: Na rodada 2, os jogadores têm a chance de aprimorar sua estratégia, uma vez que poderão escolher o par ordenado mais conveniente para eliminar peças do adversário.
Discuta com a turma:
- A sequência dos números no par ordenado permite ampliar as estratégias para eliminar as peças do adversário? Como?
- No jogo acima, qual vantagem o alunos da dupla amarela tiveram em relação à dupla vermelha?
Encerramento
Tempo sugerido: 3 minutos.
Propósito: Formalizar as definições obtidas na atividade
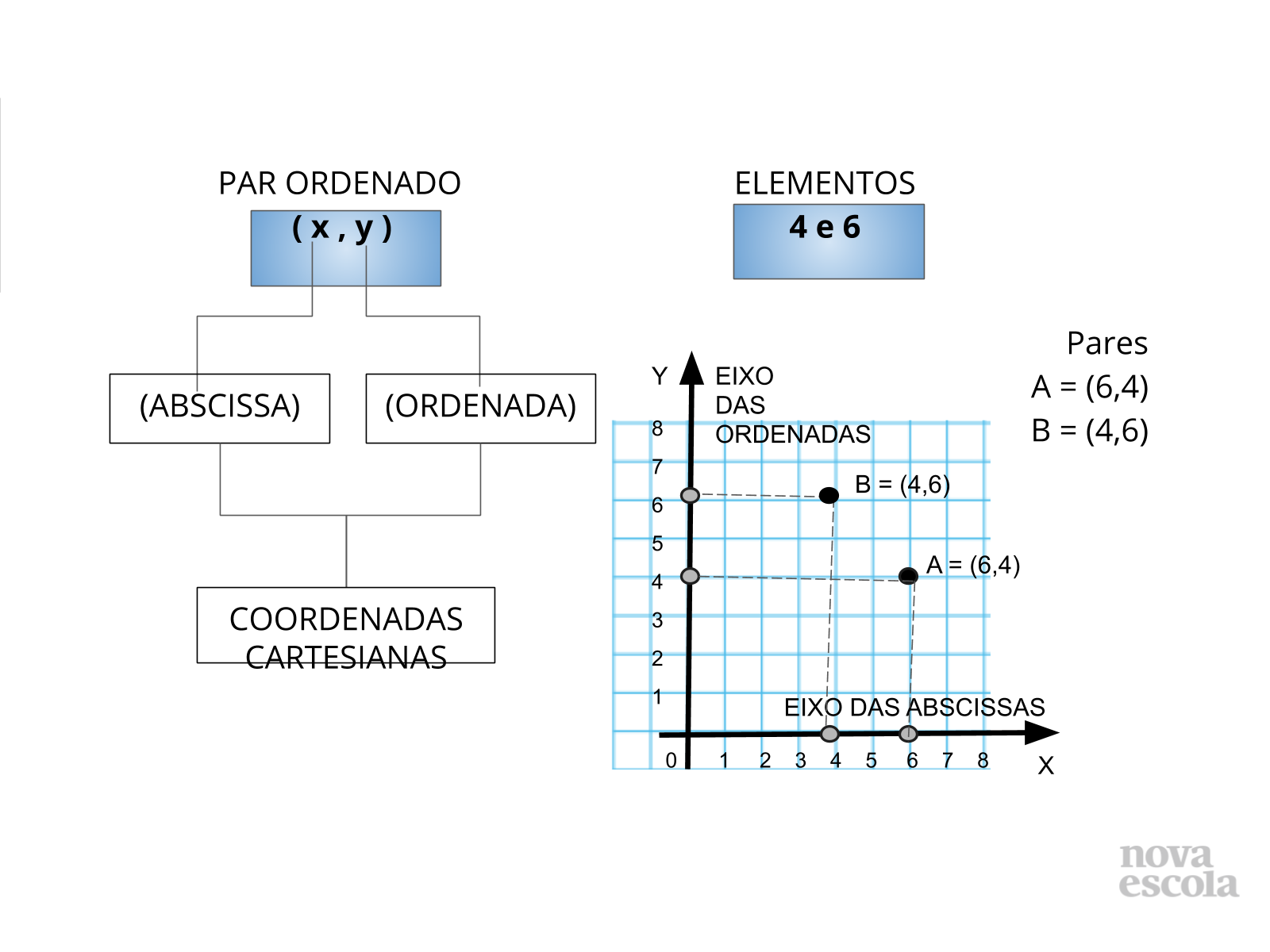
Orientação: Formaliza a definição de par ordenado e a localização de um ponto no plano através das coordenadas estabelecidas por ele. Aproveite para enfatizar o 1º elemento associando-o ao eixo das abscissas (eixo x) e o 2º elemento associando-o ao eixo das ordenadas (eixo y).
Discuta com a turma:
- Qual a posição do ponto A?
- Qual a posição do onto B?
- Pares com os mesmos elementos em posições diferentes (abscissa e ordenada) corresponde a: (espera-se que o aluno complete a frase enfatizando a divergência dos pontos).
Raio X
Tempo sugerido: 10 minutos (slides 8 e 9).
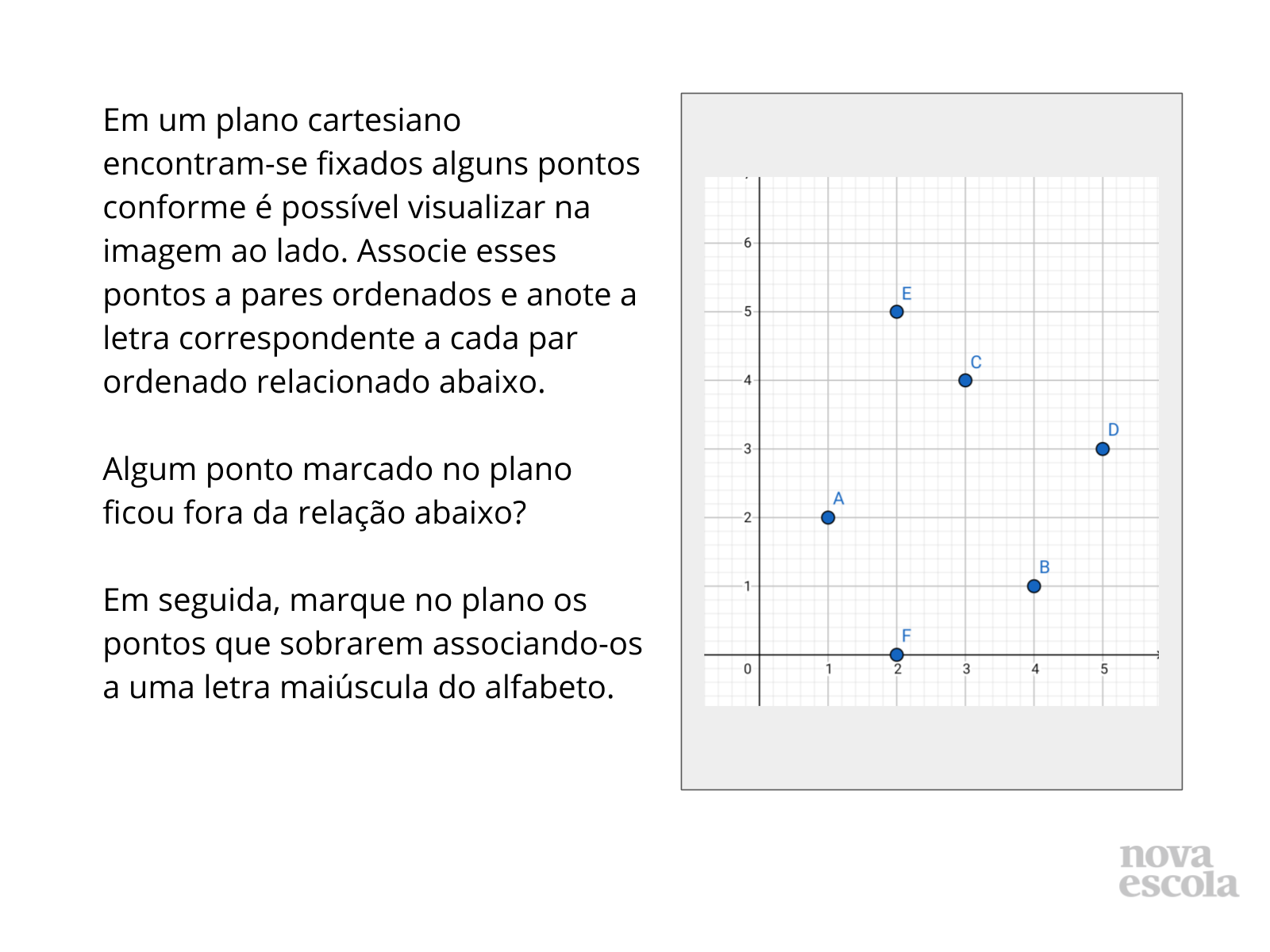
Propósito: Aplicar o conceito de par ordenado associando-os a pontos no plano cartesiano.
Orientação: Lembre o aluno a necessidade de atentar para a ordem dos pares. Espera-se que nesse momento o aluno já tenha percebido que o primeiro número do par corresponde ao eixo das abscissas e o segundo ao eixo das ordenadas. O professor pode ter acesso a atividade para impressão, assim como ao gabarito.
Discuta com a turma alguns exemplos onde os alunos possam perceber que uma inversão na ordem da escrita do par ordenado corresponde a pontos completamente diferentes no plano cartesiano.
Materiais complementares:
Atividade complementar
Atividade Raio X
Resolução da atividade complementar
Resolução do Raio X
Raio X.
Tempo sugerido: 10 minutos.
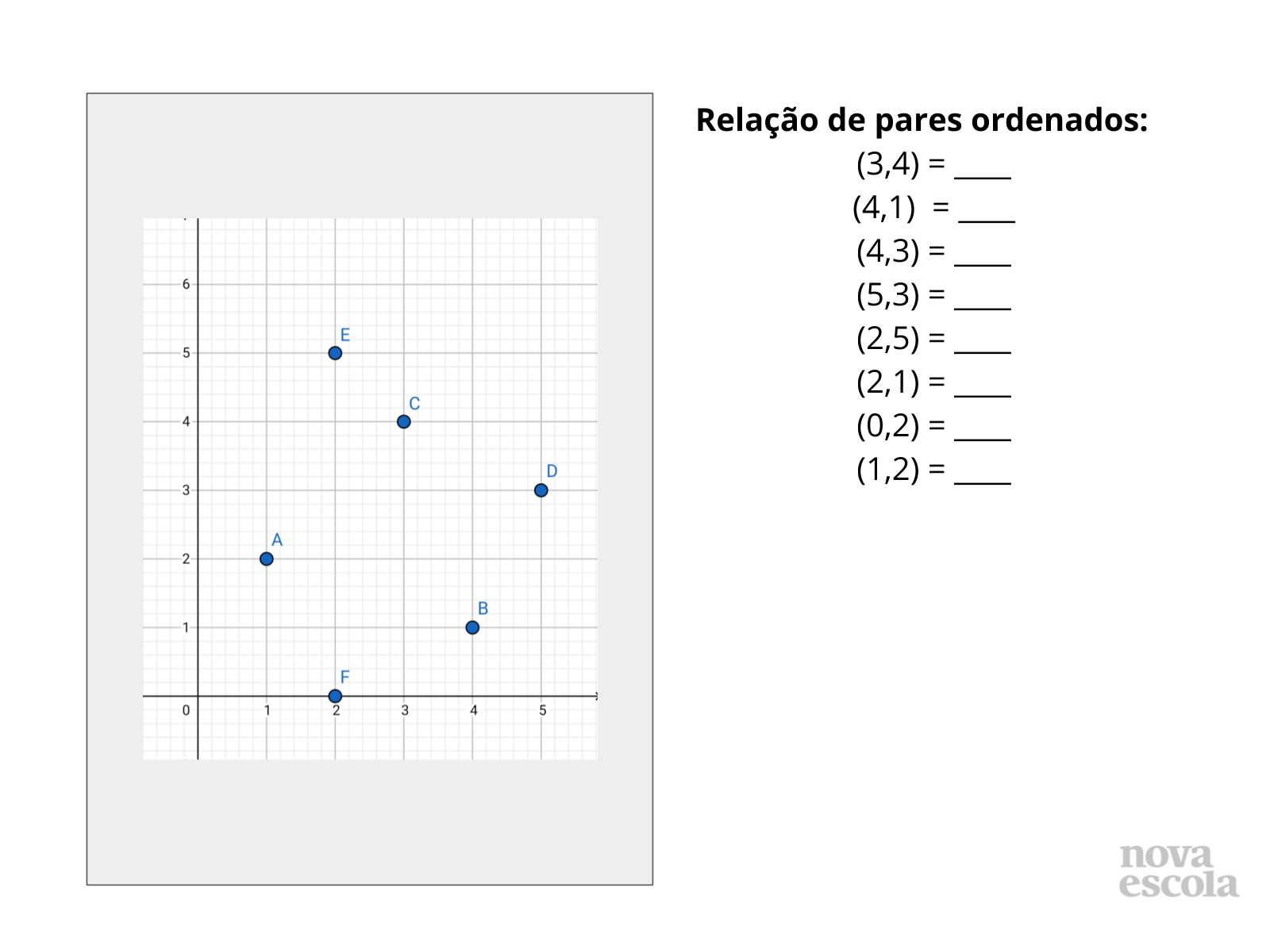
Propósito: Aplicar o conceito de par ordenado associando-os a pontos no plano cartesiano
Orientação: Lembre ao aluno a necessidade de atentar para a ordem dos pares. Espera-se que nesse momento o aluno já tenha percebido que o primeiro número do par corresponde ao eixo das abscissas e o segundo ao eixo das ordenadas. O professor pode ter acesso a atividade para impressão.
Discuta com a turma alguns exemplos onde os alunos possam perceber que uma inversão na ordem da escrita do par ordenado corresponde a pontos completamente diferentes no plano cartesiano.
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. 



















