Atividade Principal
Plano de Aula
Plano de aula: O que é espaço amostral?
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Estudos sobre probabilidade
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Graziela Ferreira de Souza
Mentora: Eunice Maria Figueira Cajango
Especialista de Área: Rita de Cássia Batista da Silva
Habilidade da BNCC
(EF05MA22) Apresentar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não.
Objetivos específicos
- Ampliar a ideia de espaço amostral por meio de experimento aleatório.
- Determinar o espaço amostral de um experimento.
Conceito-chave
Espaço amostral.
Recursos necessários
Dados, moedas e projetor de slides.
Habilidades BNCC:
Objetivos de aprendizagem
- Ampliar a ideia de espaço amostral por meio de experimento aleatório.
- Determinar o espaço amostral de um experimento.
Planeje suas aulas pelo Whatsapp!
Qualidade com economia de tempo
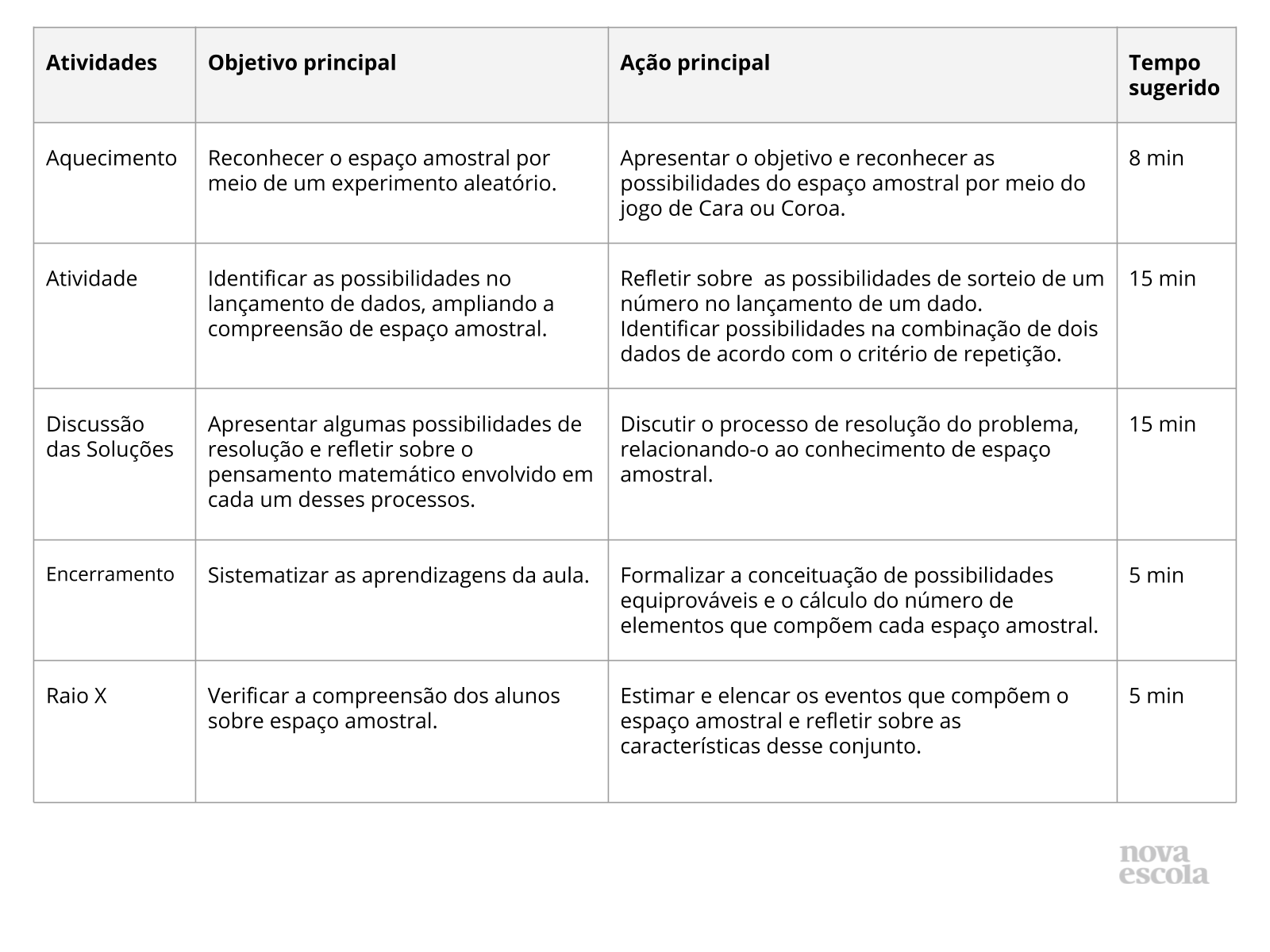
Aula
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.













