Sugestão de adaptação para ensino remoto
Ferramentas sugeridas
- Essenciais: alguma rede social (Whatsapp, Facebook etc.) e papel para anotações.
- Optativas: calculadora.
Aquecimento
Usando a rede social escolhida, lembre os alunos da diferença dos números racionais e irracionais pedindo para calcular algumas raízes quadradas e algumas equivalência entre frações e números decimais por meio de divisão. Faça suas escolhas com números racionais e irracionais.
Atividade principal
Pergunte:
- Quanto é 2 bananas + 3 bananas?
- Quanto é 5 laranjas + 3 laranjas?
- Quanto é 25 maçãs – 12 maçãs?
Aparentemente, essas são perguntas triviais e causará repostas até irônicas. Acrescente:
- Quanto é 2 bananas + 3 laranjas?
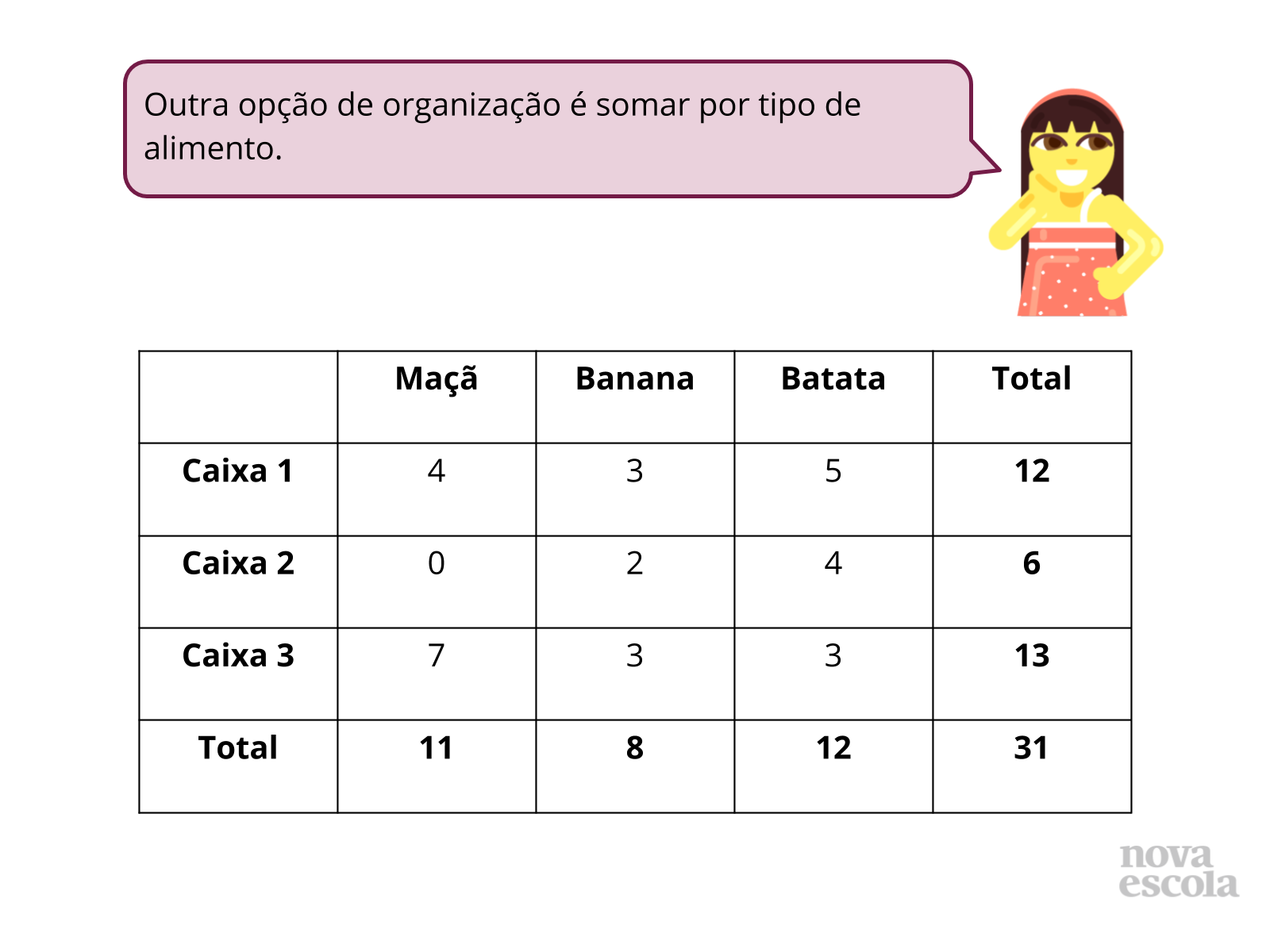
Nesse momento, as respostas tendem a ser “5 frutas”. Então chame a atenção explicando que não se pode somar ou subtrair coisas que não são semelhantes, por isso enquadraram a banana e a laranja em um outro conjunto: o das frutas.
Ofereça, agora, a opção com números:
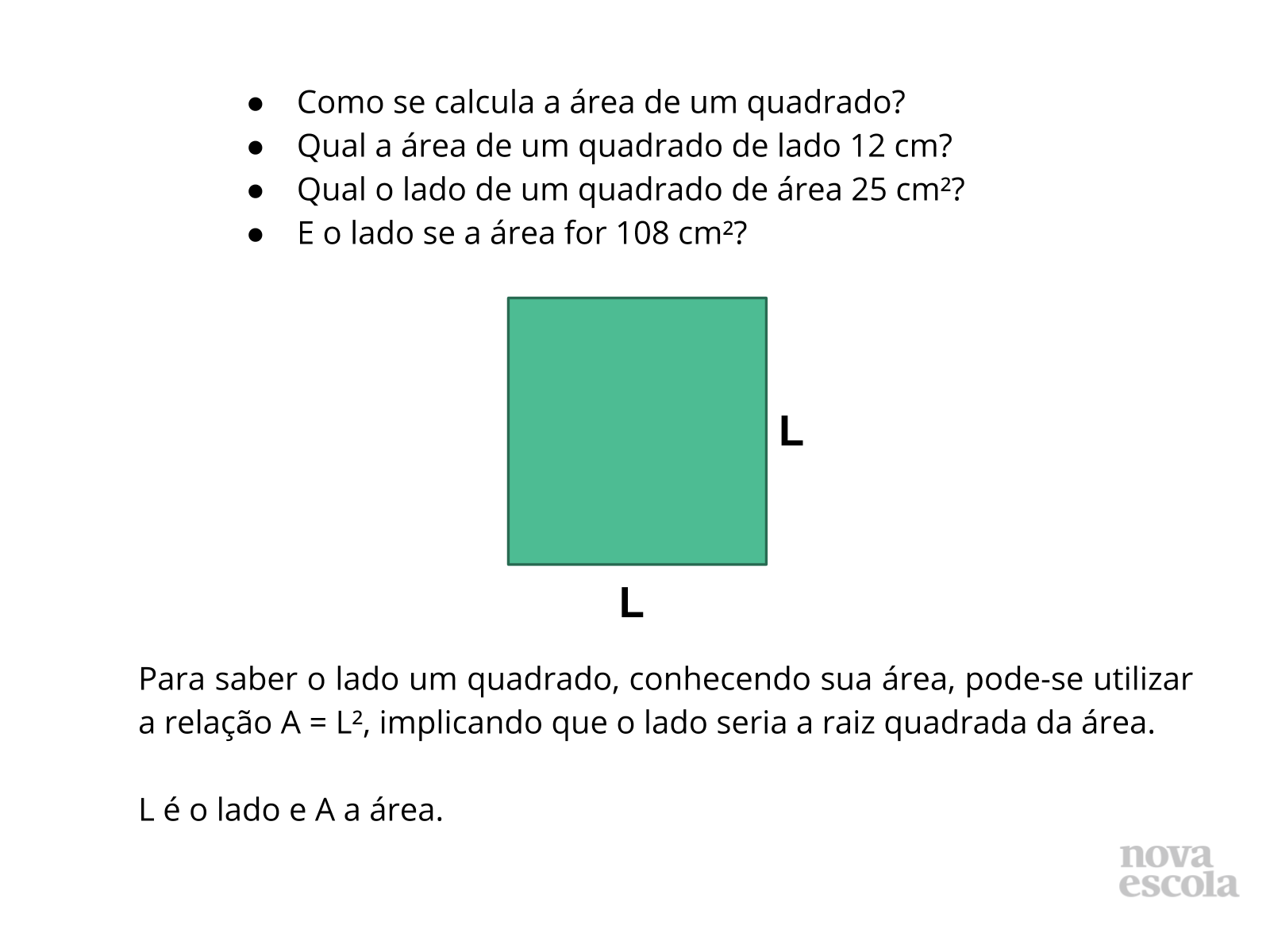
√25+√36=
√5+√3=
Pergunte a eles como responderiam e, se possível, anote as respostas para sua condução.
Agora, peça para fazerem com esses (aqui, já os incentive a fazer a fatoração e usar a notação de potência para ajudarem a verem regularidades):
√75-√27=
Espere as respostas.
Painel de soluções
Agora faça um retorno às frutas. Pergunte:
- Se não tivesse a possibilidade de chamar a banana e a laranja como (pertencente ao conjunto) frutas, qual seria então a resposta?
Aguarde um pouco e diga que a resposta seria: "2 bananas + 3 laranjas, pois não podemos somar coisas que não são semelhantes".
Assim, pensando nos números, mostre:
√25+√36=5+6=11 (pois, na verdade, são racionais).
√5+√3= 5+3 (pois, são irracionais e de radicais diferentes).
√75-√27= 5√3-3√3 (pois, 75=5².3 e 27=3³-aqui procuramos potências de 2, logo, podemos escrever 27=3².3).
Dessa forma, podemos fazer: √75-√27= 5√3-3√3=2√3.
Sistematização
Ressalte que assim também se pensa com os números:
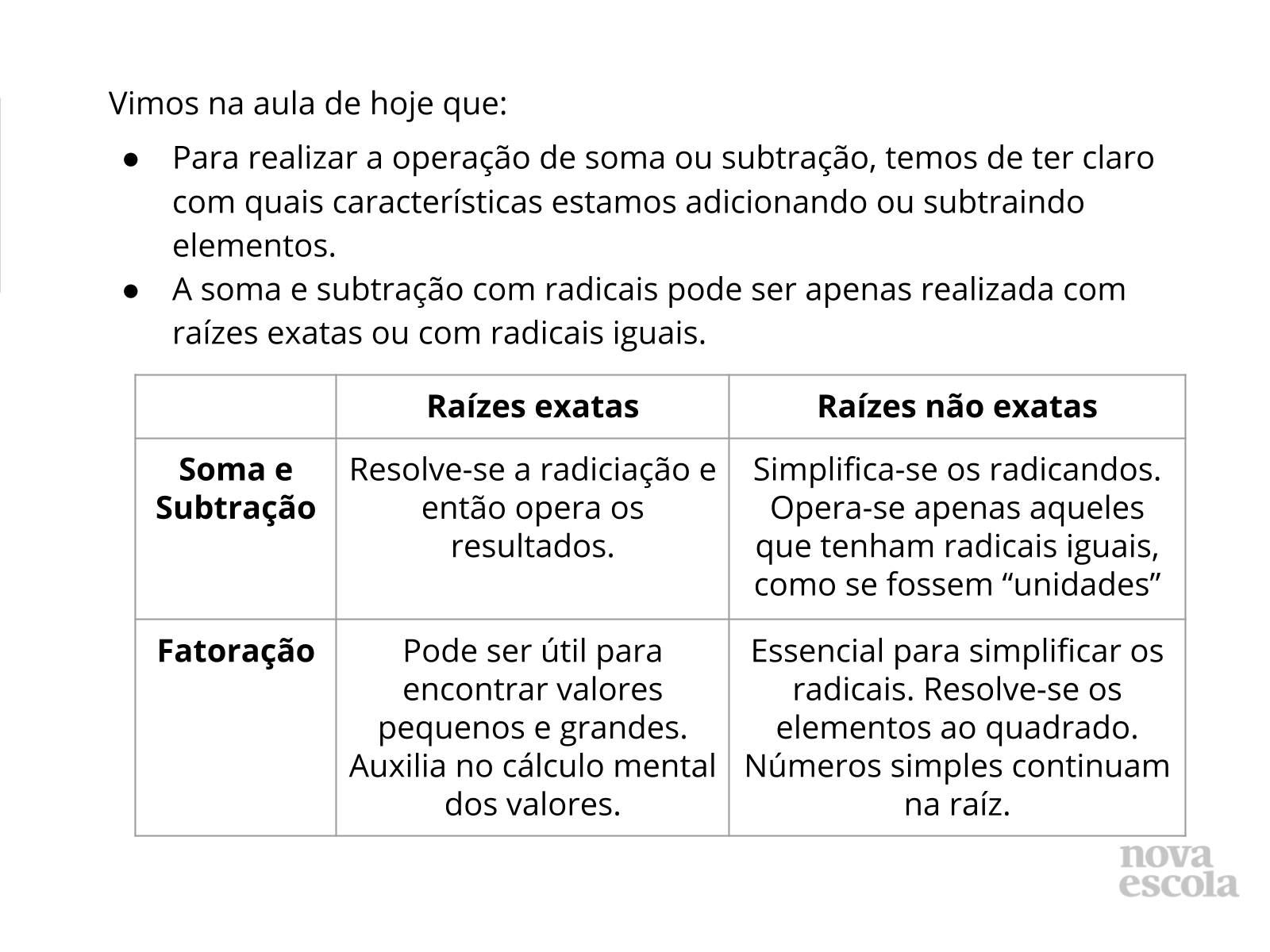
- Racionais só podem ser somados com racionais;
- No caso dos irracionais, que são raízes “não-exatas”, só podem ser somados (ou subtraídos) se tiverem o mesmo radical.
Encerramento
Ressalte a importância de se saber fatorar quando for preciso somar ou subtrair radicais.
Raio X
Peça para que seus alunos proponham algumas questões uns para os outros e dê suporte, quando necessário.
Convite às famílias
Peça para seus alunos verificarem com os familiares, próximos neste momento, a resposta para uma soma de objetos não semelhantes. Provavelmente, os chamarão apenas de “objetos” nas respostas.
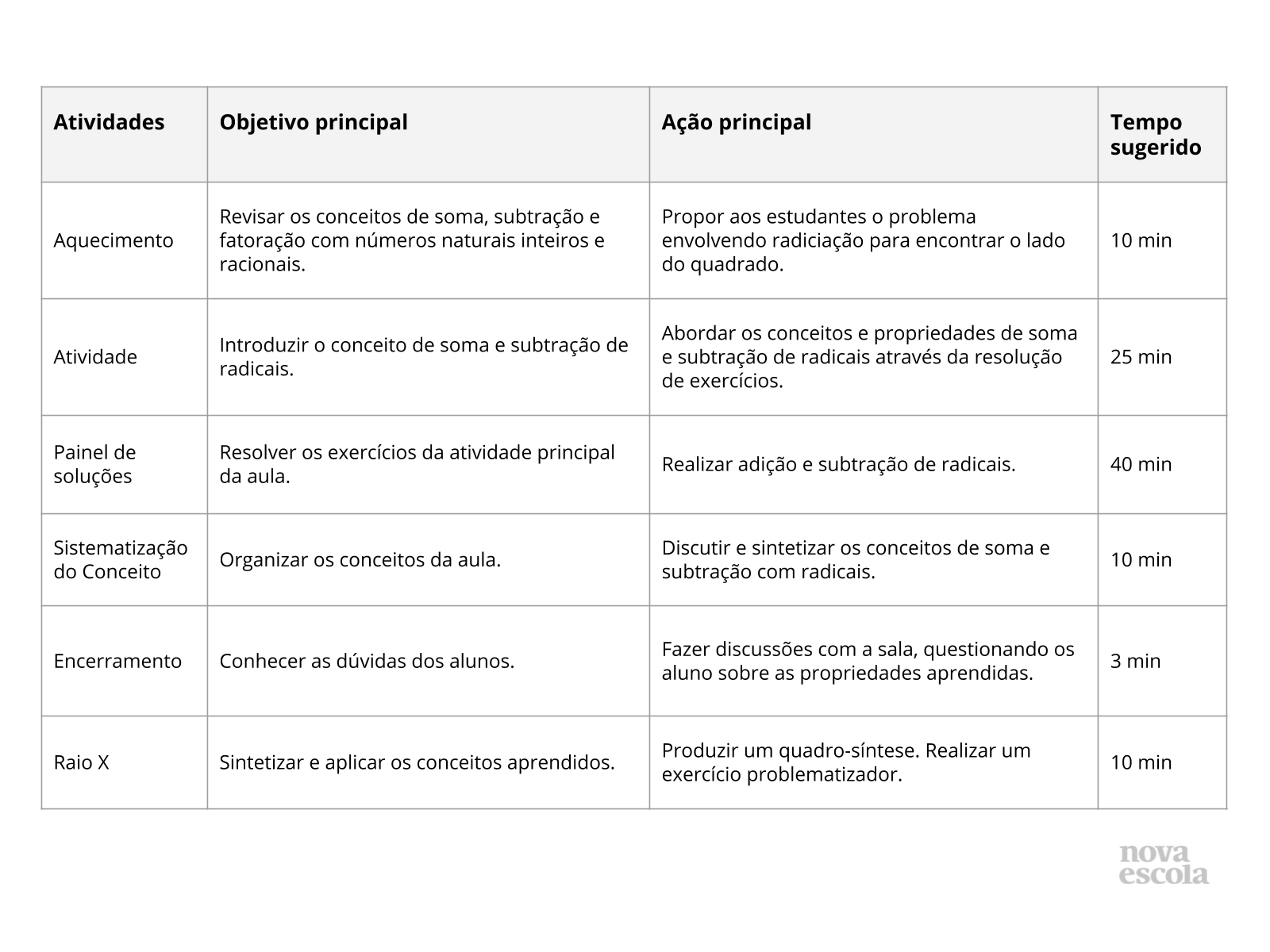 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.