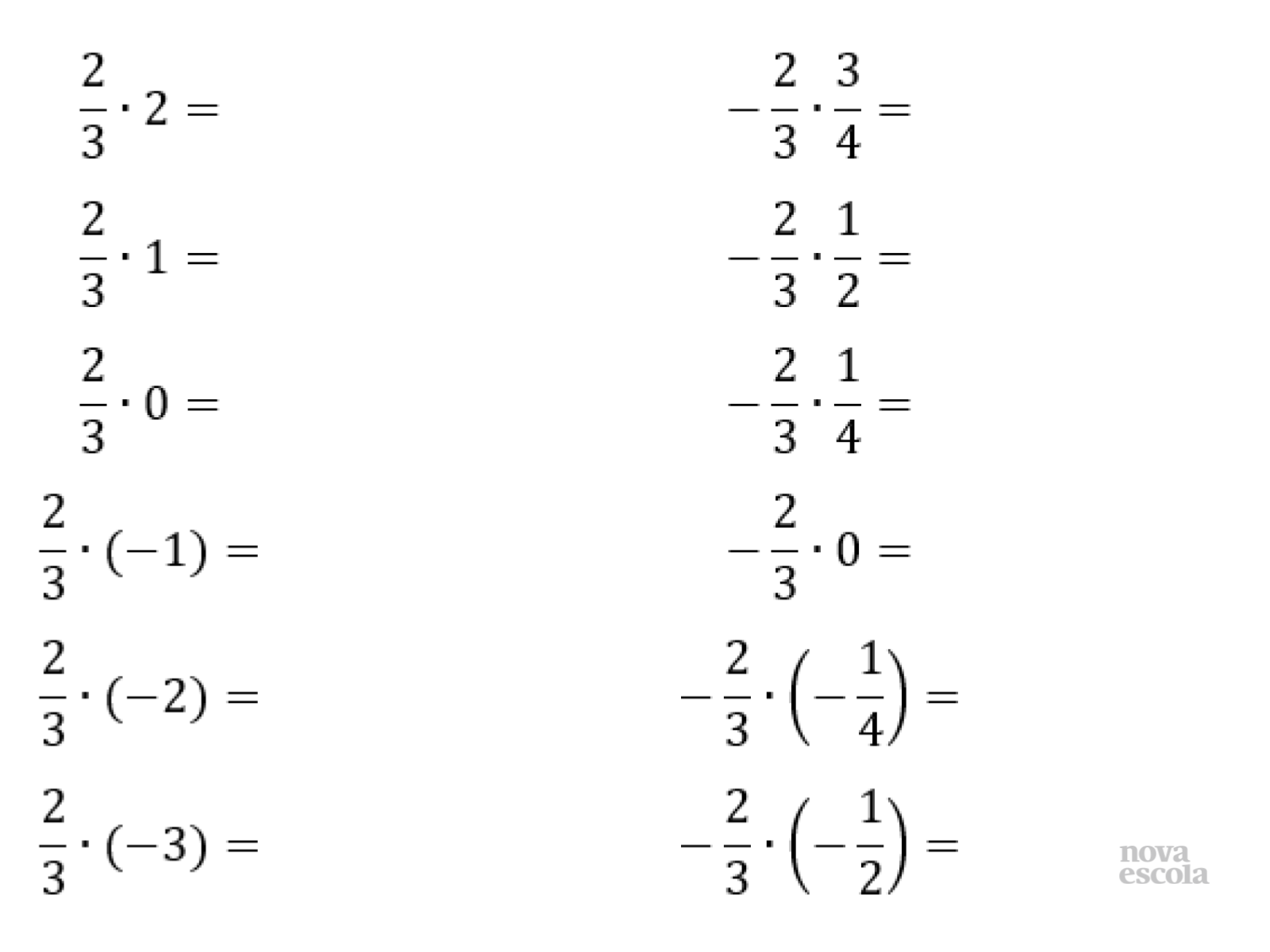Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Apresentar o objetivo da aula de maneira breve, mostrando ao aluno o foco da aula, sem desconsiderar que ele precisará dos conceitos adquiridos anteriormente referente aos números naturais, inteiros e racionais.
Propósito: compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 6 minutos.
Orientação: Apresente para os alunos as operações resolvidas e faça as perguntas que estão no slide. Você pode projetar esse slide ou escrever as operações na lousa e fazer as perguntas oralmente. O objetivo é trazer para a aula os conhecimentos prévios sobre a regra de sinais usada na multiplicação e sobre o algoritmo da multiplicação de frações.
Discuta com a turma:
- Todo número multiplicado por zero é sempre zero? Isso vale para negativos? E para frações?
- Todo número multiplicado por 1 é ele mesmo? Isso vale para negativos? E para frações?
- O que acontece quando multiplicamos um número por -1?
- Como podemos multiplicar uma fração por um número inteiro? É preciso transformar o inteiro em fração? Se sim, como fazemos isso?
Propósito: Relembrar operações que envolvam números inteiros (positivos e negativos) e números racionais positivos na forma fracionária.
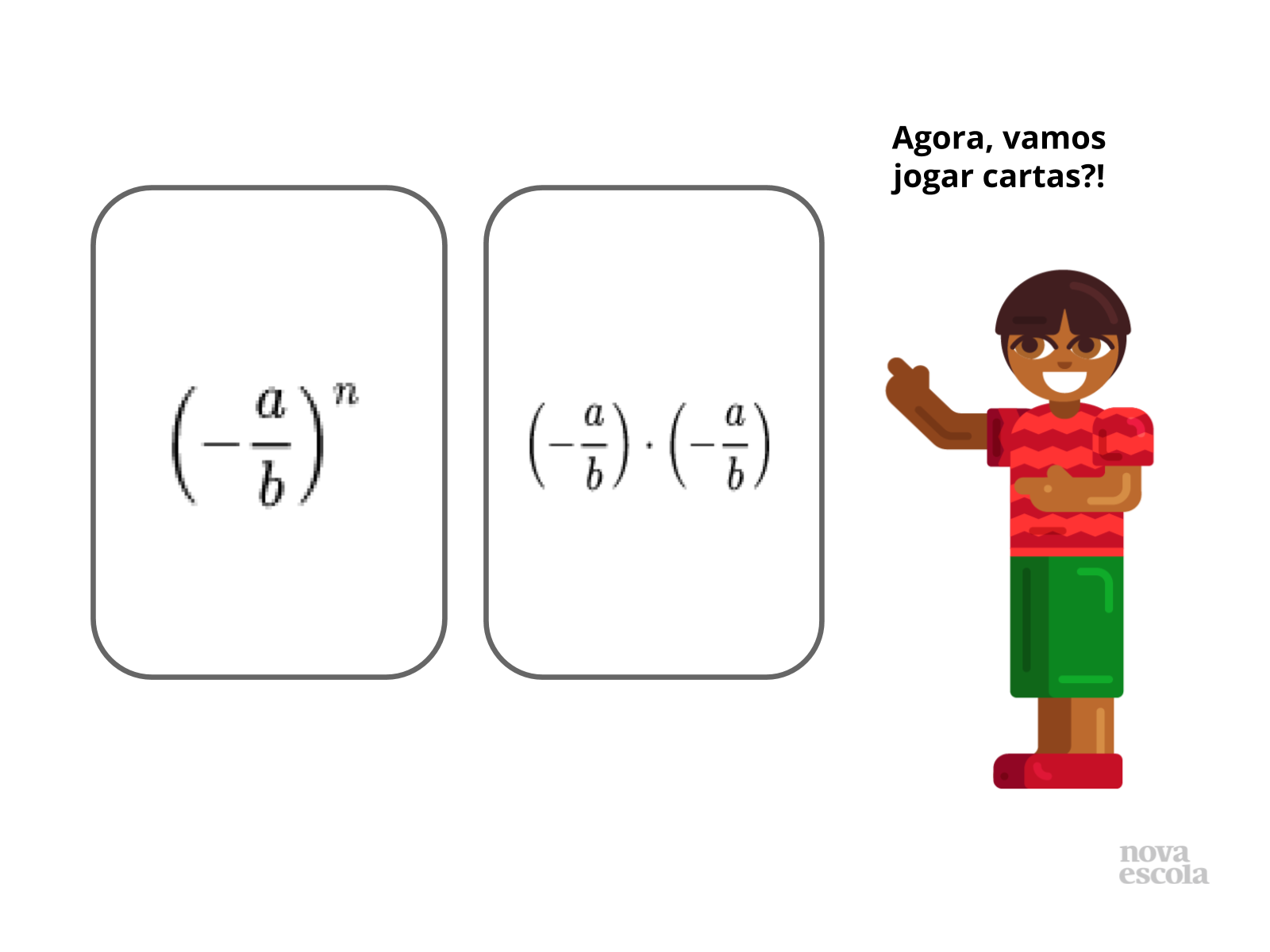
Atividade Principal (slides 4 e 5)

Tempo sugerido: 20 minutos.
Orientação: Organize a sala da maneira que preferir. A organização em duplas pode auxiliar na troca de informações, mas nesse caso é essencial que os alunos reflitam um pouco sozinhos sobre as operações, procedimentos e estratégias pessoais, antes de interagir com a dupla. Apresente os questionamentos presentes no slide 4, peça que reflitam sobre eles e em seguida peça que resolvam as questões do slide 5.
Você pode apresentar essas questões no slide, escrevê-las na lousa ou entregar a atividade impressa para os alunos. Reforce com eles que eles podem resolver as operações como preferirem: descobrindo estratégias aritméticas novas, utilizando recursos tecnológicos ou ainda utilizando representações visuais.
Discuta com a turma:
- A propriedade comutativa da multiplicação é válida nos racionais?
- Existem frações negativas?
- É possível multiplicar uma fração por um inteiro negativo?
Propósito: Oportunizar os alunos a aprender um novo conceito através do esforço produtivo.
Materiais complementares:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Atividade Principal (slides 4 e 5)
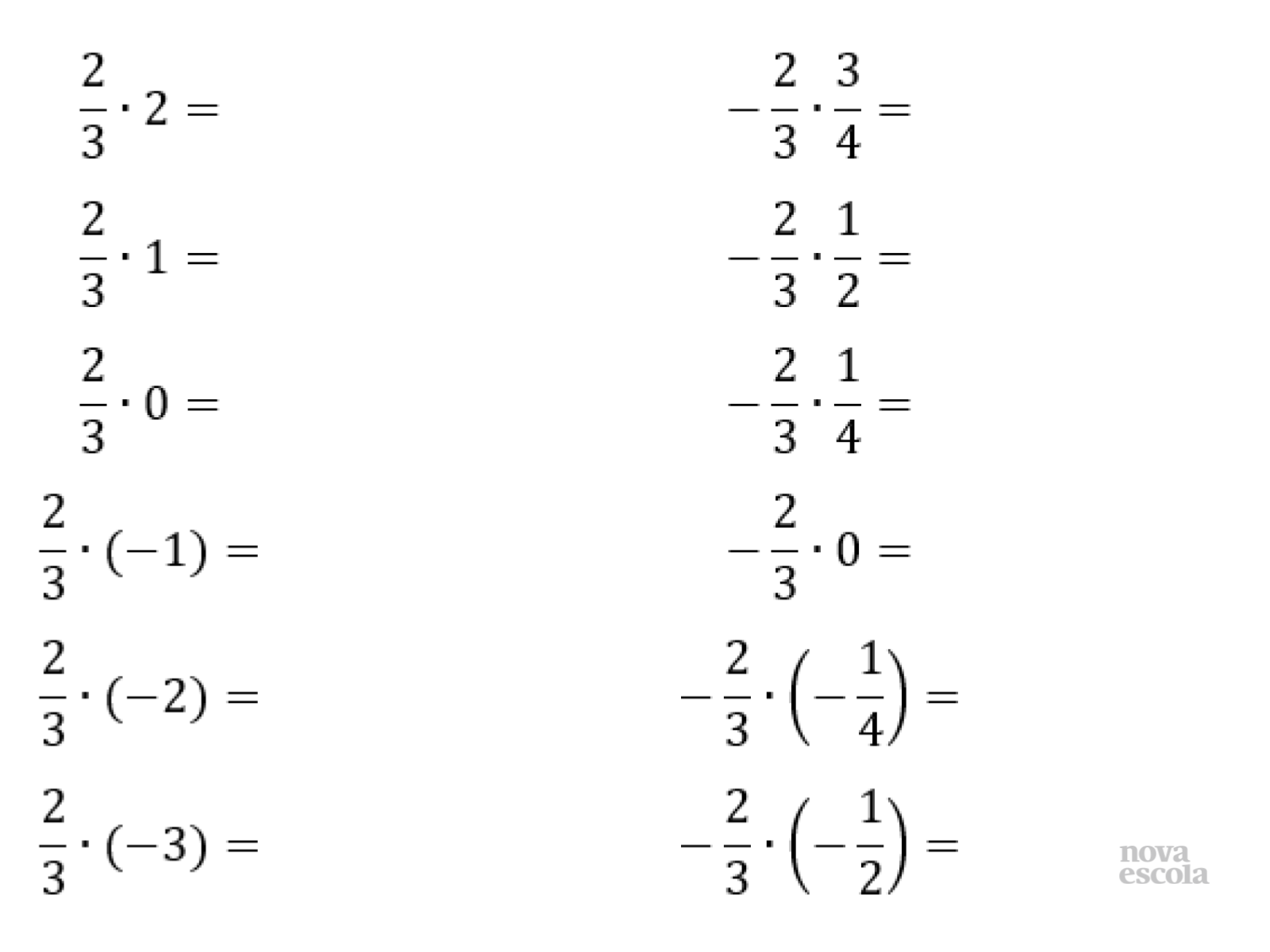
Tempo sugerido: 20 minutos.
Orientação: Organize a sala da maneira que preferir. A organização em duplas pode auxiliar na troca de informações, mas nesse caso é essencial que os alunos reflitam um pouco sozinhos sobre as operações, procedimentos e estratégias pessoais, antes de interagir com a dupla. Apresente os questionamentos presentes no slide 4, peça que reflitam sobre eles e em seguida peça que resolvam as questões do slide 5.
Você pode apresentar essas questões no slide, escrevê-las na lousa ou entregar a atividade impressa para os alunos. Reforce com eles que eles podem resolver as operações como preferirem: descobrindo estratégias aritméticas novas, utilizando recursos tecnológicos ou ainda utilizando representações visuais.
Discuta com a turma:
- A propriedade comutativa da multiplicação é válida nos racionais?
- Existem frações negativas?
- É possível multiplicar uma fração por um inteiro negativo?
Propósito: Oportunizar os alunos a aprender um novo conceito através do esforço produtivo.
Discussão da solução (slides 6 e 7)

Tempo sugerido: 10 minutos.
Orientação: Peça aos alunos para que apresentem suas respostas para as operações. Anote as respostas na lousa (mesmo as erradas) pedindo que cada aluno explique as diferentes respostas, mostrando as estratégias utilizadas. Peça aos alunos para que confrontem suas ideias até que cheguem a um consenso sobre as respostas das operações.
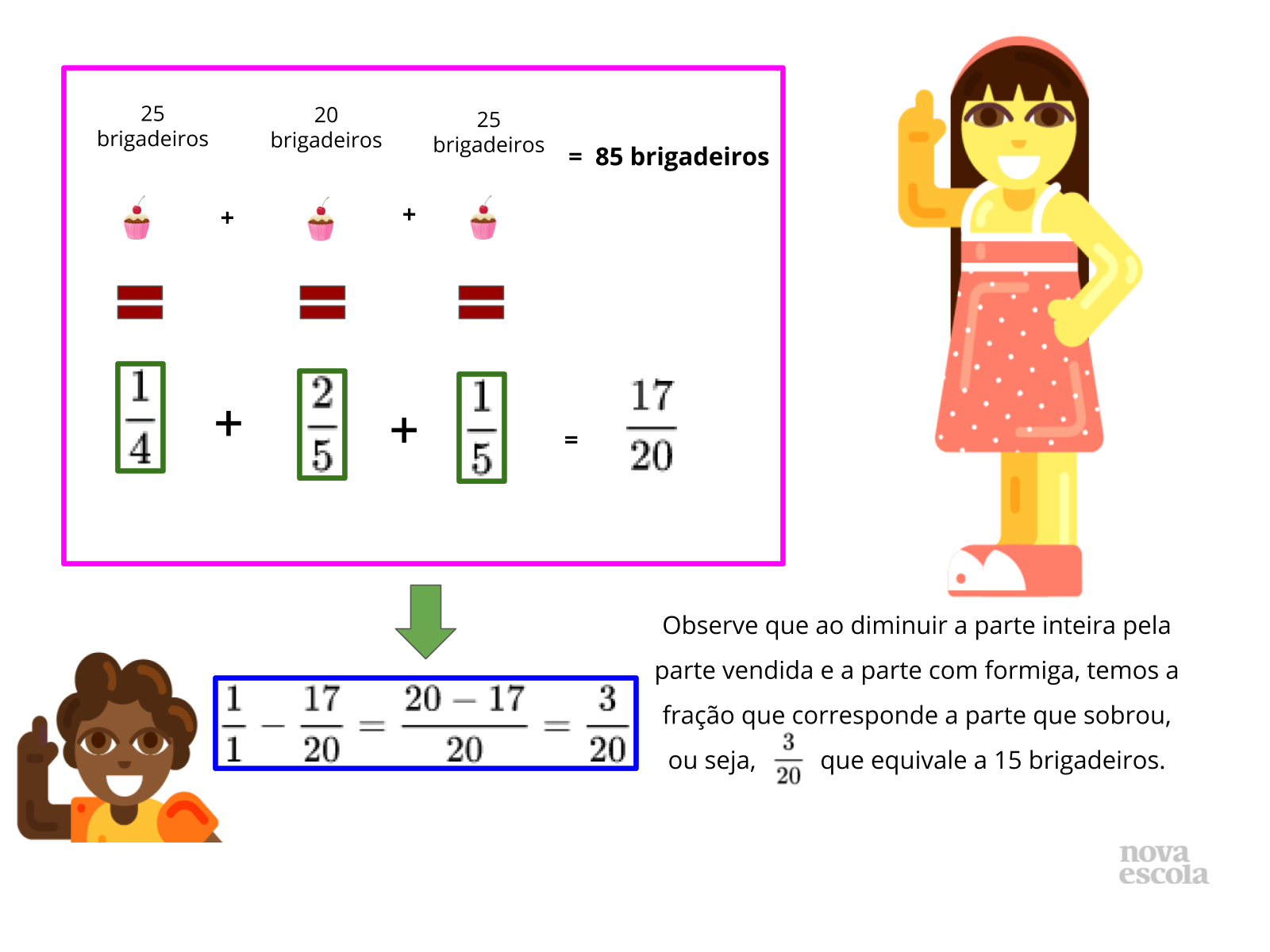
Com base nas respostas corretas das multiplicações e nas conclusões trazidas pelos alunos, leve-os a perceber que multiplicar um número (inteiro ou não) por uma fração é o mesmo que calcular parte desse número. Desse modo, nem sempre o resultado será maior que o próprio número.
Seguindo esse raciocínio, os alunos devem perceber, por exemplo, que multiplicar um número (inteiro ou não) por 3/2 é o mesmo que obter uma parte e meia desse número. Desse modo, a multiplicação não pode ser vista como soma de parcelas iguais, já que para interpretar a multiplicação como adição é preciso compreender tamanhos diferentes de parcelas, sendo ao menos uma menor que as outras.
Propósito: chegar à solução da questão a partir das propostas de resolução dadas pelos alunos
Discussão da solução (slides 6 e 7)

Tempo sugerido: 10 minutos.
Orientação: Peça aos alunos para que apresentem suas respostas para as operações. Anote as respostas na lousa (mesmo as erradas) pedindo que cada aluno explique as diferentes respostas, mostrando as estratégias utilizadas. Peça aos alunos para que confrontem suas ideias até que cheguem a um consenso sobre as respostas das operações.
Com base nas respostas corretas das multiplicações e nas conclusões trazidas pelos alunos, leve-os a perceber que multiplicar um número (inteiro ou não) por uma fração é o mesmo que calcular parte desse número. Desse modo, nem sempre o resultado será maior que o próprio número.
Seguindo esse raciocínio, os alunos devem perceber, por exemplo, que multiplicar um número (inteiro ou não) por 3/2 é o mesmo que obter uma parte e meia desse número. Desse modo, a multiplicação não pode ser vista como soma de parcelas iguais, já que para interpretar a multiplicação como adição é preciso compreender tamanhos diferentes de parcelas, sendo ao menos uma menor que as outras.
Propósito: chegar à solução da questão a partir das propostas de resolução dadas pelos alunos
Sistematização (slides 8 e 9)

Tempo sugerido: 3 minutos.
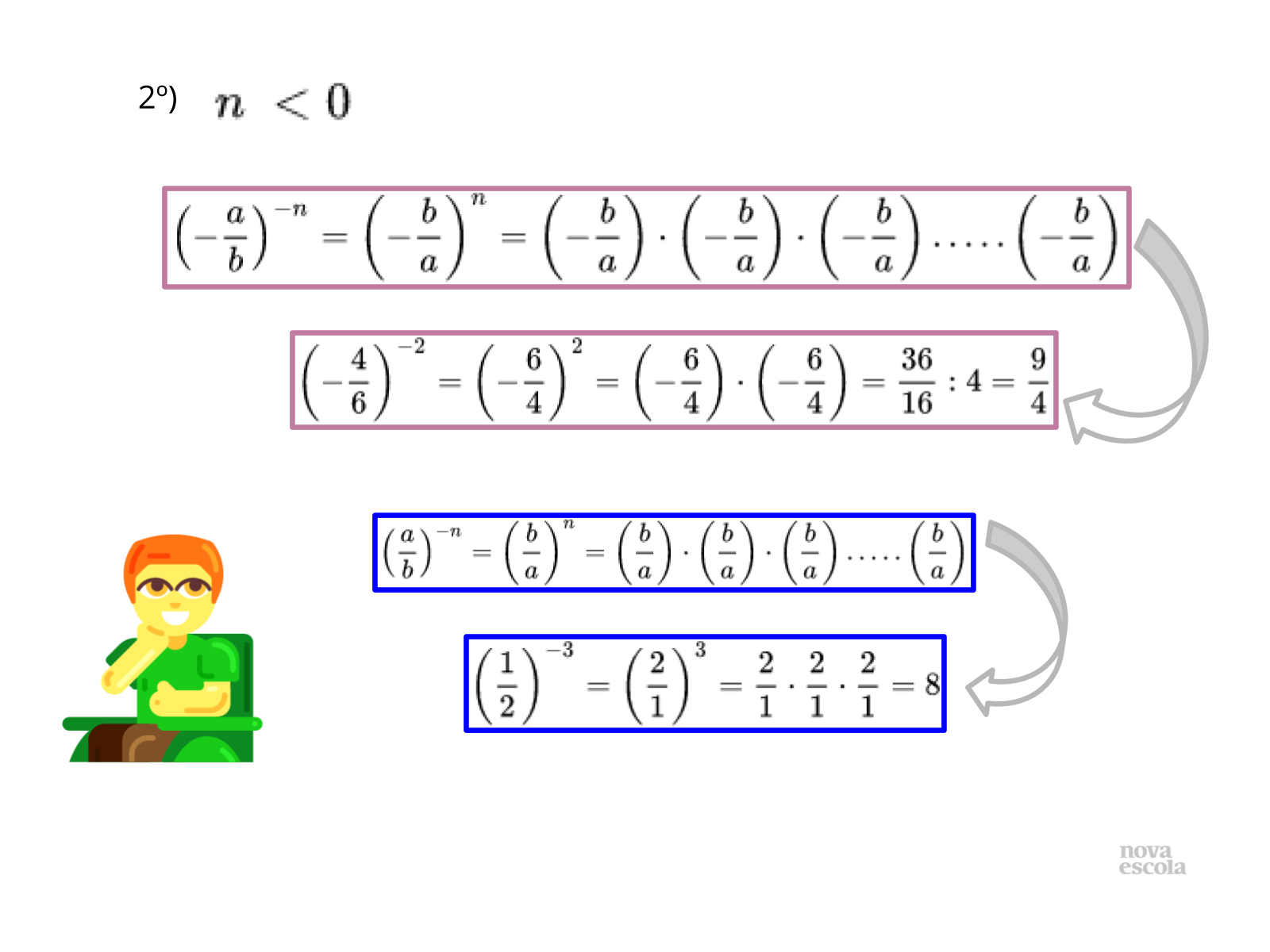
Orientação: Apresente esses slides ou escreva na lousa as regras formais da multiplicação de racionais. Relembre-os da regra de sinal e da multiplicação entre numeradores e denominadores separadamente. Mostre que algumas propriedades continuam válidas: elemento neutro, elemento oposto, comutativa e multiplicação por zero.
Utilize essas conclusões para justificar o fato de que a multiplicação não é uma operação que “aumenta” o número e nem sempre pode ser vista como uma soma de parcelas iguais.
Propósito: sistematizar o conhecimento da aula, formalizando os conceitos.
Sistematização (slides 8 e 9)

Tempo sugerido: 3 minutos.
Orientação: Apresente esses slides ou escreva na lousa as regras formais da multiplicação de racionais. Relembre-os da regra de sinal e da multiplicação entre numeradores e denominadores separadamente. Mostre que algumas propriedades continuam válidas: elemento neutro, elemento oposto, comutativa e multiplicação por zero.
Utilize essas conclusões para justificar o fato de que a multiplicação não é uma operação que “aumenta” o número e nem sempre pode ser vista como uma soma de parcelas iguais.
Propósito: sistematizar o conhecimento da aula, formalizando os conceitos.
Encerramento

Tempo sugerido: 2 minutos.
Orientação: Peça aos alunos para que verifiquem se as operações dadas aqui são o suficiente para exemplificar tudo o que foi sistematizado.
Propósito: Apresentar o que foi aprendido durante essa aula de maneira resumida.
Raio X
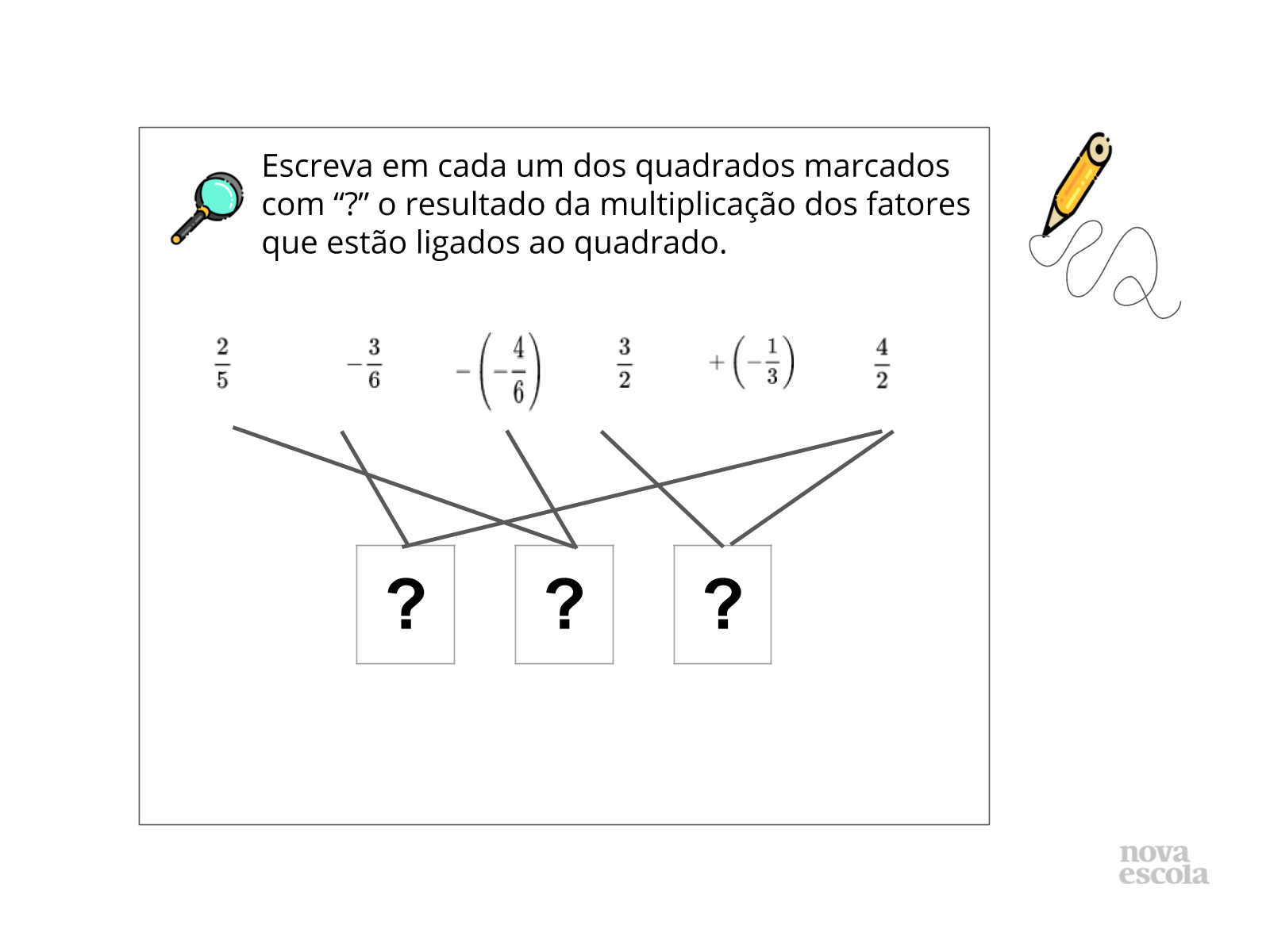
Tempo sugerido: 7 minutos.
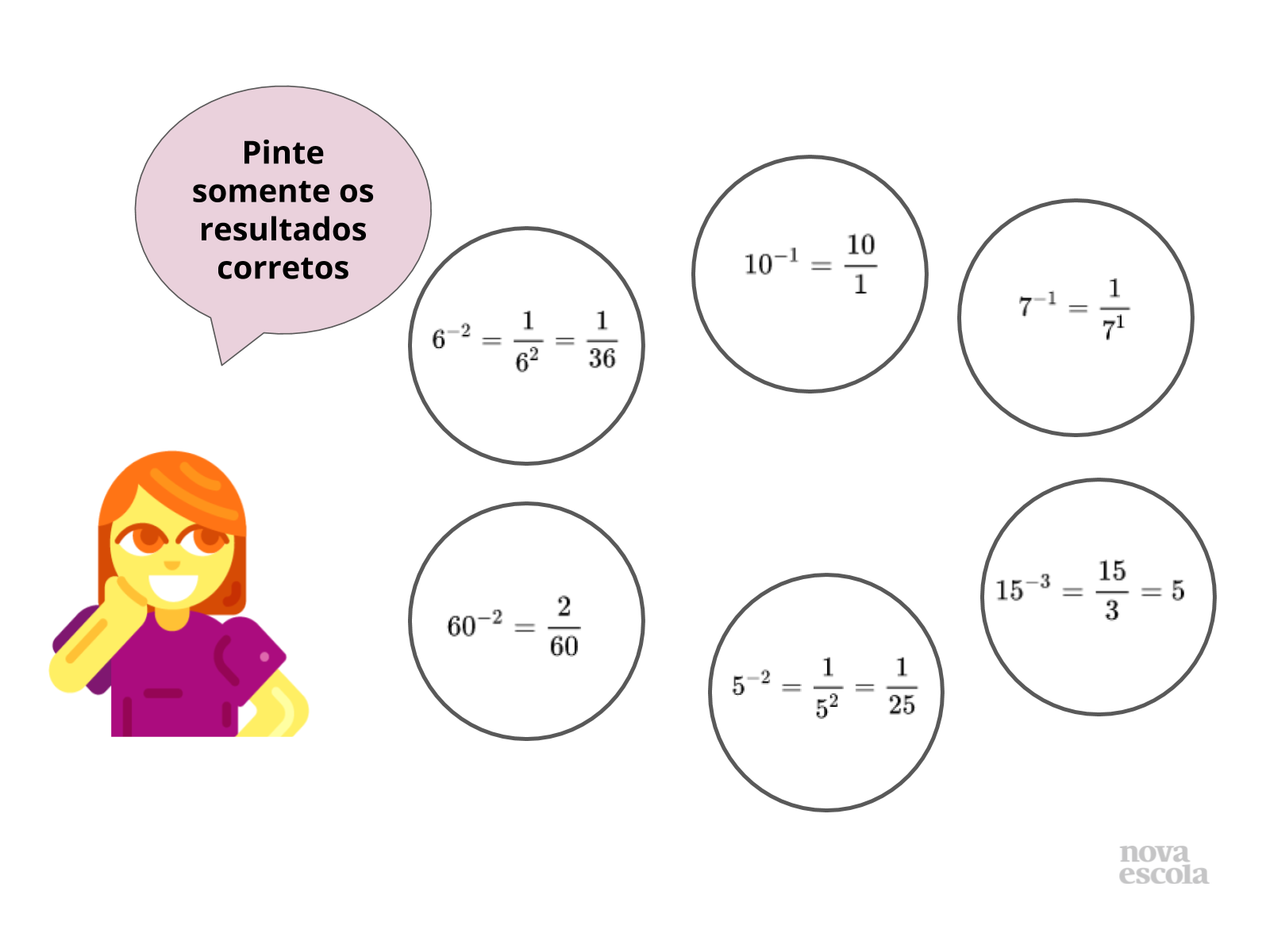
Orientação: nessa atividade, o objetivo é avaliar o progresso do aluno através de sugestões e possíveis erros que permitam finalizar a abordagem, identificando aspectos relevantes da aprendizagem do aluno ligada a identificação dos racionais fracionários positivos e negativos, aplicação das regras de sinais, utilização do princípio de multiplicação entre esses números.
Propósito: Avaliar o progresso do aluno.
Materiais complementares:
Raio X
Resolução do Raio X
Atividade complementar
Resolução da Atividade Complementar