Objetivo
O valor Numérico de uma Expressão Algébrica
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Geraldo Prado
Mentor: Rhômulo Oliveira Menezes
Especialista de área: Sandra Regina Correa Amorim
Habilidade da BNCC
(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.
Objetivos Específicos
Calcular o valor numérico de uma expressão algébrica, envolvendo conhecimentos algébricos e geométricos.
Conceito-chave
Valor numérico de uma expressão algébrica.
Recursos necessários
- Folha de papel A4 ou similar (caderno);
- Atividades impressas.
Tempo sugerido: 2 minutos.
Orientações: Projete o slide ou escreva no quadro o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento
Tempo sugerido: 5 minutos.
Orientações: Utilize o Aquecimento também como uma retomada do conceito de expressões, diferenciando expressões algébricas das numéricas.
Ao questionar sobre a opinião dos alunos a respeito das falas de João, Gustavo e Maria, deixe que eles se sintam livres para encontrar semelhanças e/ou diferenças entre os exemplos. É provável que algum aluno aponte o fato de que as expressões citadas por Gustavo e João, tenham letras, enquanto que a de Maria, não!
Este será, então, o momento propício para retomar e reforçar o que são as expressões algébricas, a saber:
- Expressões algébricas são expressões matemáticas que apresentam números, letras e operações.
- As expressões desse tipo são usadas com frequência em fórmulas e equações.
- As letras que aparecem em uma expressão algébrica são chamadas de variáveis e representam um valor desconhecido.
- Os números escritos com as letras são chamados de coeficientes e deverão ser multiplicados pelos valores atribuídos às letras.
Propósito: Apresentar o conceito de expressão algébrica, diferenciando-as das expressões numéricas.
Atividade Principal
Tempo sugerido: 15 minutos. (Slides 4, 5 e 6).
Orientações: Peça que, individualmente, os alunos leiam a atividade e desenvolvam estratégias para poder responder aos questionamentos. Em seguida, deixe que discutam com um colega suas soluções. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
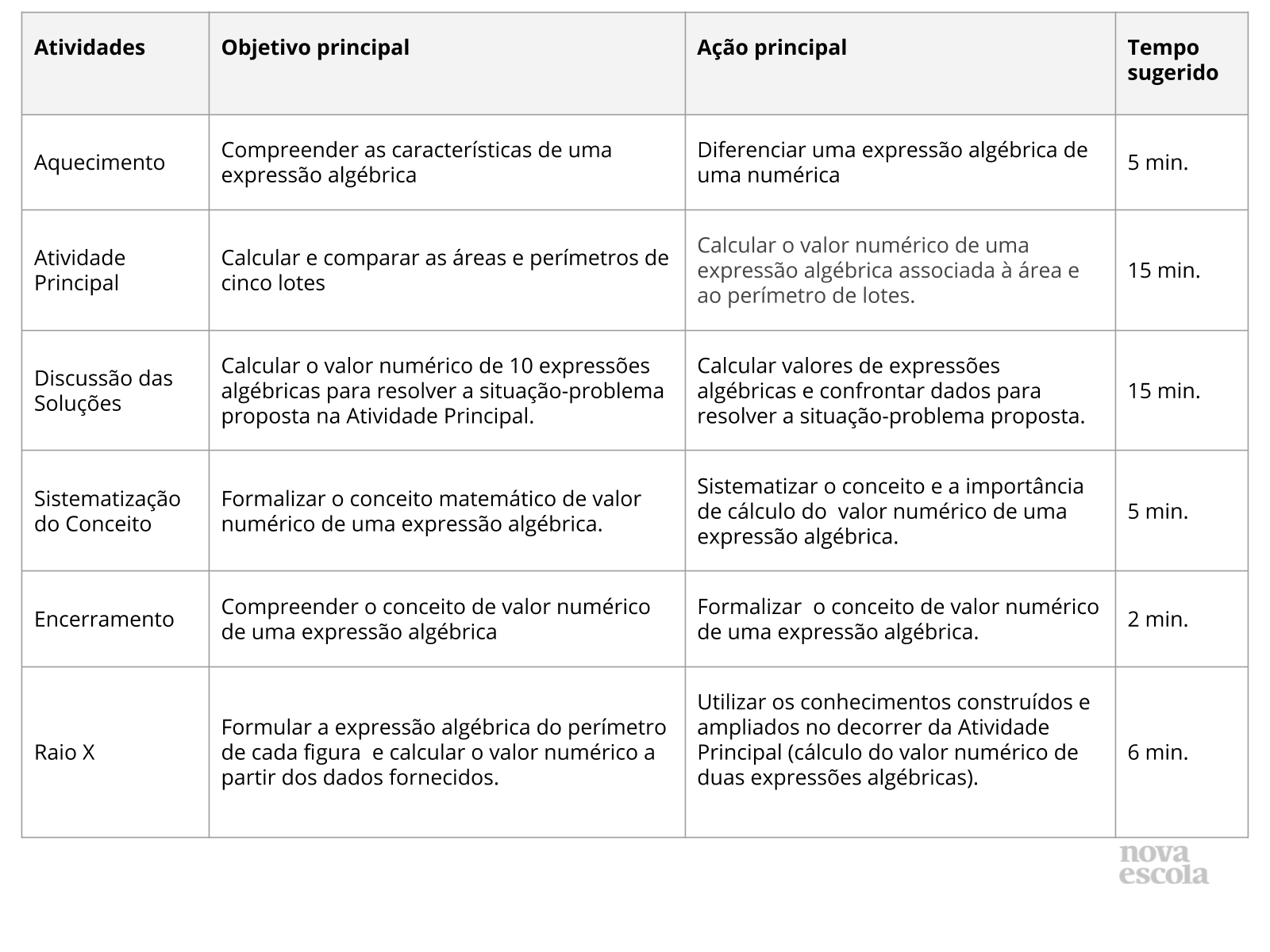
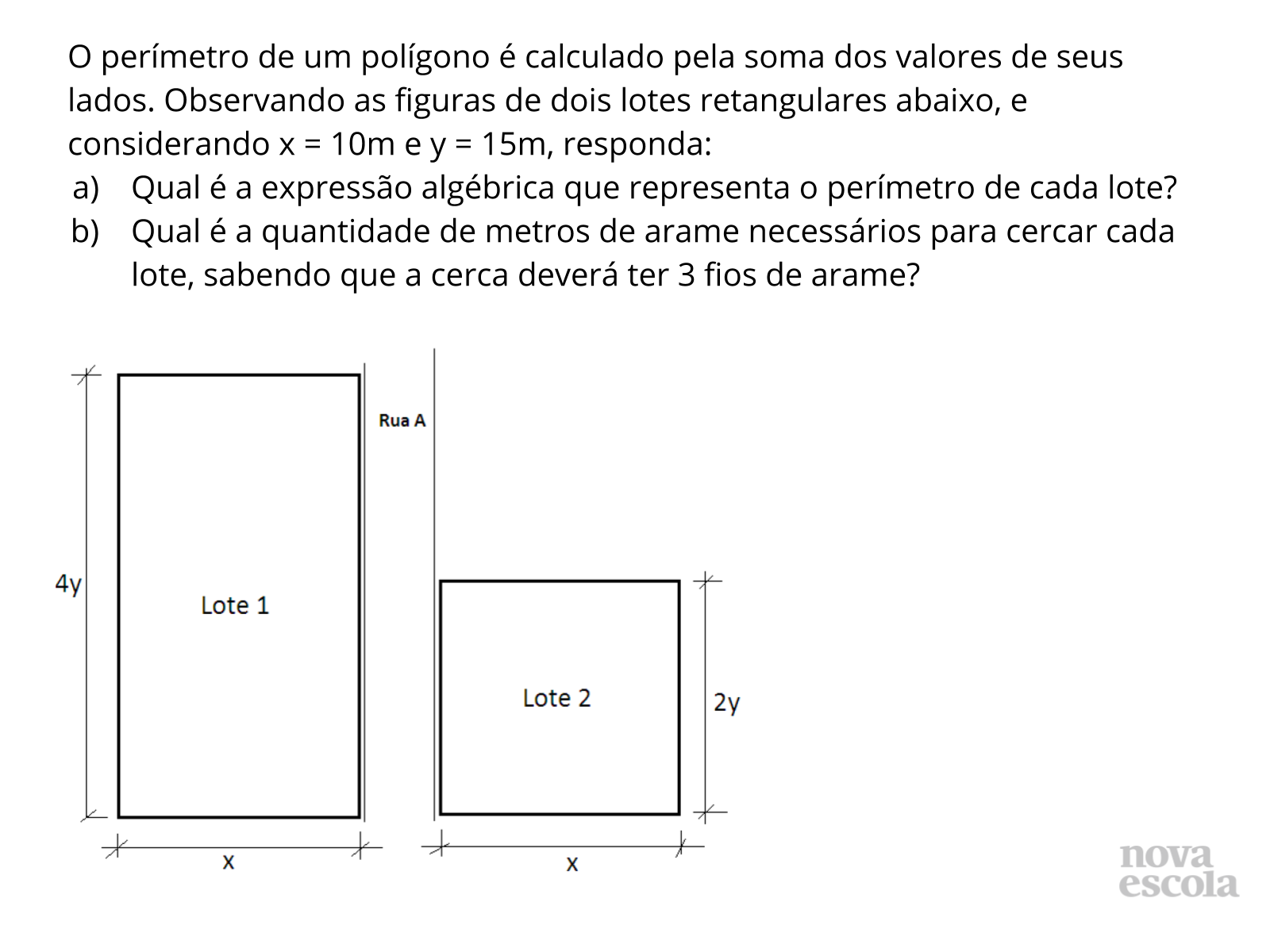
Para um melhor entendimento da tarefa, é necessário que os alunos já conheçam previamente o conceito de área de uma figura plana (apresentado no slide 4). No caso das opções de terrenos abordados no problema, consideramos que eles têm formatos retangulares, logo, a área é calculada como o produto do comprimento pela largura de cada lote. A atividade também faz menção ao perímetro de cada lote, por isso lembre aos alunos que o perímetro é a soma dos lados de um polígono.
Propósito: Fazer com que os alunos encontrem o valor numérico de uma expressão algébrica por meio do cálculo da área e do perímetro de cada lote.
Discuta com a Turma:
- Como calcular a área de cada terreno?
- Como calcular o perímetro de cada terreno?
- Como calcular o valor de cada terreno?
Materiais Complementares:
Atividade Principal
Tempo sugerido: 15 minutos. (Slides 4, 5 e 6).
Orientações: Peça que, individualmente, os alunos leiam a atividade e desenvolvam estratégias para poder responder aos questionamentos. Em seguida, deixe que discutam com um colega suas soluções. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
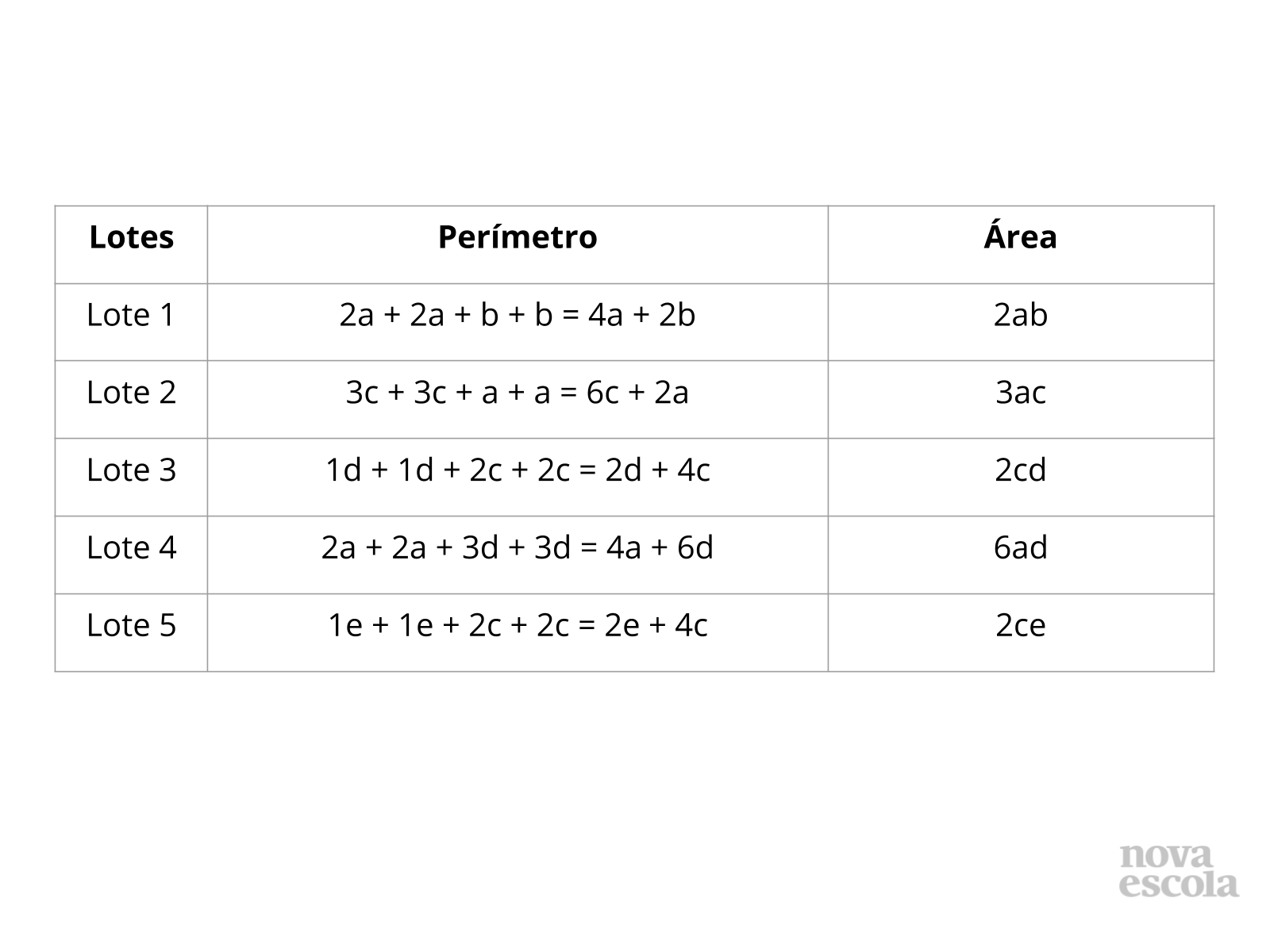
Para um melhor entendimento da tarefa, é necessário que os alunos já conheçam previamente o conceito de área de uma figura plana (apresentado no slide 4). No caso das opções de terrenos abordados no problema, consideramos que eles têm formatos retangulares, logo, a área é calculada como o produto do comprimento pela largura de cada lote. A atividade também faz menção ao perímetro de cada lote, por isso lembre aos alunos que o perímetro é a soma dos lados de um polígono.
Propósito: Fazer com que os alunos encontrem o valor numérico de uma expressão algébrica por meio do cálculo da área e do perímetro de cada lote.
Discuta com a Turma:
- Como calcular a área de cada terreno?
- Como calcular o perímetro de cada terreno?
- Como calcular o valor de cada terreno?
Atividade Principal
Tempo sugerido: 15 minutos. (Slides 4, 5 e 6).
Orientações: Peça que, individualmente, os alunos leiam a atividade e desenvolvam estratégias para poder responder aos questionamentos. Em seguida, deixe que discutam com um colega suas soluções. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Para um melhor entendimento da tarefa, é necessário que os alunos já conheçam previamente o conceito de área de uma figura plana (apresentado no slide 4). No caso das opções de terrenos abordados no problema, consideramos que eles têm formatos retangulares, logo, a área é calculada como o produto do comprimento pela largura de cada lote. A atividade também faz menção ao perímetro de cada lote, por isso lembre aos alunos que o perímetro é a soma dos lados de um polígono.
Propósito: Fazer com que os alunos encontrem o valor numérico de uma expressão algébrica por meio do cálculo da área e do perímetro de cada lote.
Discuta com a Turma:
- Como calcular a área de cada terreno?
- Como calcular o perímetro de cada terreno?
- Como calcular o valor de cada terreno?
Discussão das Soluções
Tempo sugerido: 15 minutos. (Slides 7, 8 e 9).
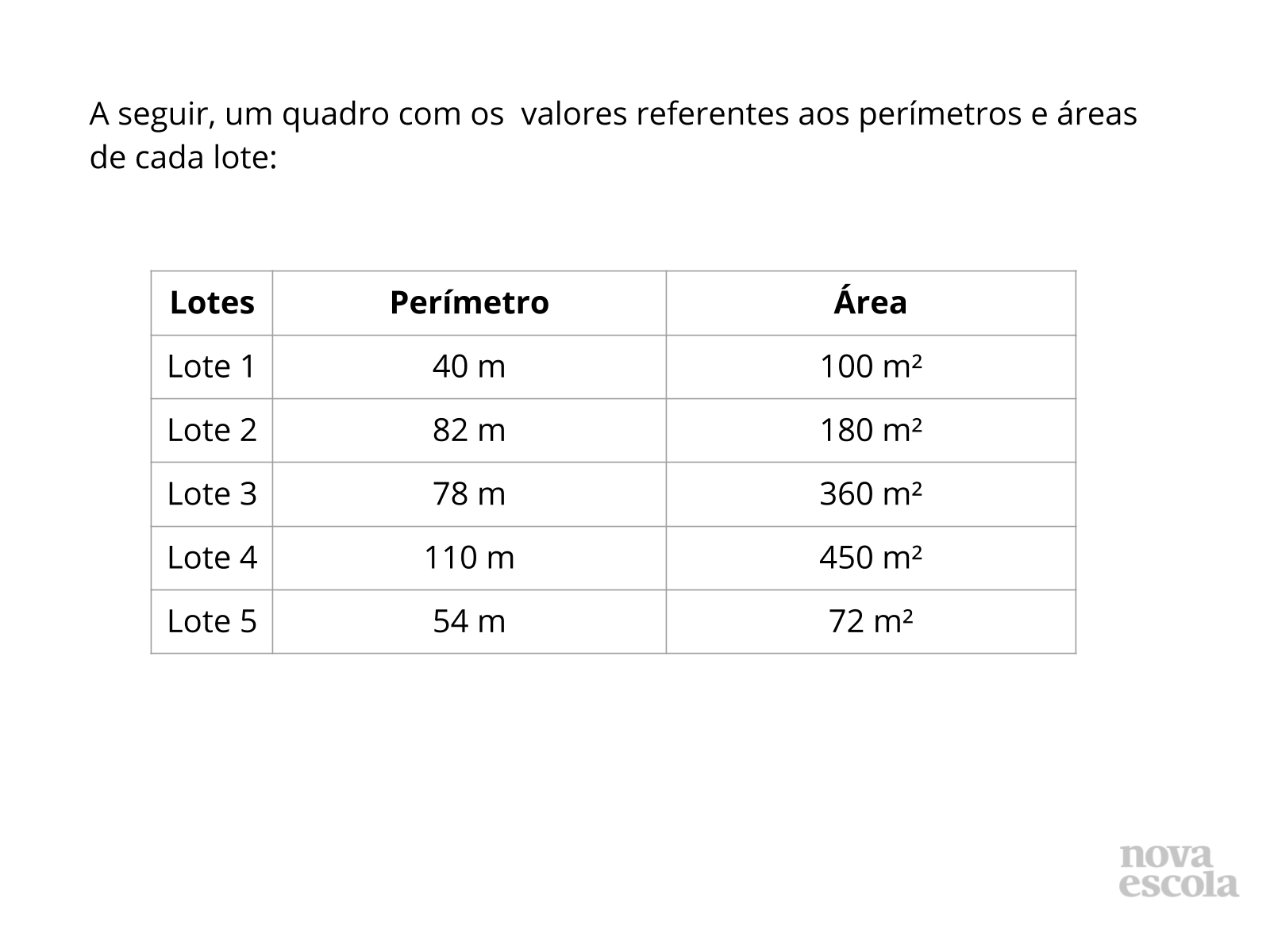
Orientações: Escolha alguns alunos que apresentaram maneiras diferentes de solucionar o problema para ir ao quadro. O número de alunos pode ser escolhido segundo as resoluções apresentadas, o ideal é que suas resoluções tenham sido diferentes. Essa diferença de resolução se dará na tomada de decisões quanto a forma de solucionar as questões do problema. Identifique e selecione essas decisões durante o tempo em que estão trabalhando na resolução, já que estará transitando pela sala, de carteira em carteira, acompanhando-os. À propósito, nesta etapa de acompanhamento, é fundamental que não dê as respostas prontas aos alunos, mas sim proponha, por meio de questionamentos, formas de raciocínio. Quando esses alunos estiverem se apresentando, à frente da turma, dê especial atenção à linguagem utilizada no procedimento. Se o aluno conseguiu expressar claramente seu raciocínio sem ter feito uso da linguagem matemática formal, aceite sem interferências. Deixe que as formalizações sejam feitas no momento oportuno, ao final da aula, na etapa de Sistematização do Conceito. Para isto, utilize o material das dicas para o professor para organizar a linguagem e uso correto dos termos envolvidos na resolução. Peça aos alunos que registrem os diferentes raciocínios que tiveram no caderno. Se tiver um projetor à sua disposição, apresente os slides como apoio à sua explicação.
Propósito: Mostrar aos alunos a aplicabilidade do valor numérico de uma expressão algébrica em uma situação-problema que envolve a medição e comparação de medidas de lotes de terrenos.
Discussão das Soluções
Tempo sugerido: 15 minutos. (Slides 7, 8 e 9).
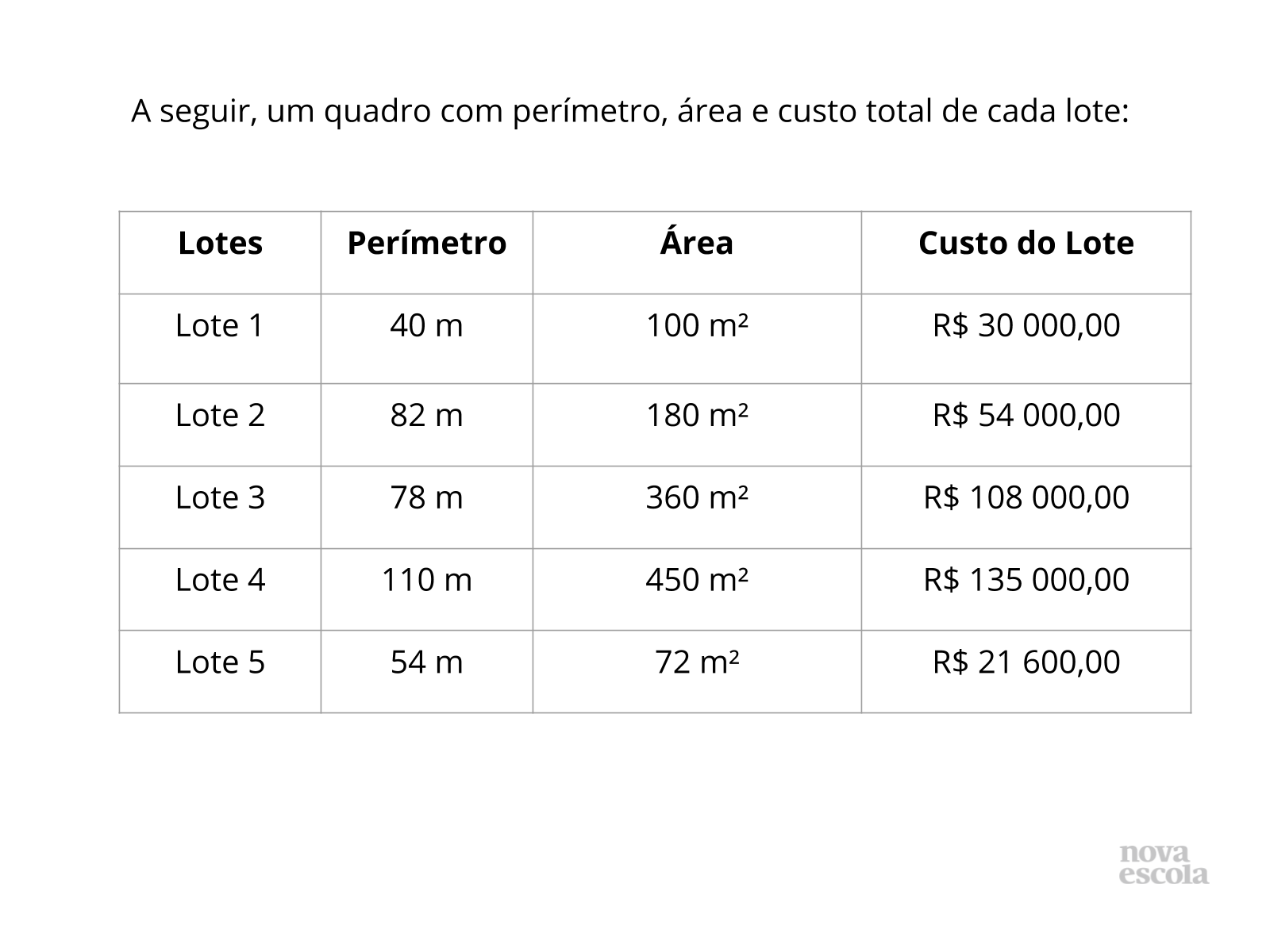
Orientações: Escolha alguns alunos que apresentaram maneiras diferentes de solucionar o problema para ir ao quadro. O número de alunos pode ser escolhido segundo as resoluções apresentadas, o ideal é que suas resoluções tenham sido diferentes. Essa diferença de resolução se dará na tomada de decisões quanto a forma de solucionar as questões do problema. Identifique e selecione essas decisões durante o tempo em que estão trabalhando na resolução, já que estará transitando pela sala, de carteira em carteira, acompanhando-os. À propósito, nesta etapa de acompanhamento, é fundamental que não dê as respostas prontas aos alunos, mas sim proponha, por meio de questionamentos, formas de raciocínio. Quando esses alunos estiverem se apresentando, à frente da turma, dê especial atenção à linguagem utilizada no procedimento. Se o aluno conseguiu expressar claramente seu raciocínio sem ter feito uso da linguagem matemática formal, aceite sem interferências. Deixe que as formalizações sejam feitas no momento oportuno, ao final da aula, na etapa de Sistematização do Conceito. Para isto, utilize o material das dicas para o professor para organizar a linguagem e uso correto dos termos envolvidos na resolução. Peça aos alunos que registrem os diferentes raciocínios que tiveram no caderno. Se tiver um projetor à sua disposição, apresente os slides como apoio à sua explicação.
Propósito: Mostrar aos alunos a aplicabilidade do valor numérico de uma expressão algébrica em uma situação-problema que envolve a medição e comparação de medidas de lotes de terrenos.
Discussão das Soluções
Tempo sugerido: 15 minutos. (Slides 7, 8 e 9).
Orientações: Escolha alguns alunos que apresentaram maneiras diferentes de solucionar o problema para ir ao quadro. O número de alunos pode ser escolhido segundo as resoluções apresentadas, o ideal é que suas resoluções tenham sido diferentes. Essa diferença de resolução se dará na tomada de decisões quanto a forma de solucionar as questões do problema. Identifique e selecione essas decisões durante o tempo em que estão trabalhando na resolução, já que estará transitando pela sala, de carteira em carteira, acompanhando-os. À propósito, nesta etapa de acompanhamento, é fundamental que não dê as respostas prontas aos alunos, mas sim proponha, por meio de questionamentos, formas de raciocínio. Quando esses alunos estiverem se apresentando, à frente da turma, dê especial atenção à linguagem utilizada no procedimento. Se o aluno conseguiu expressar claramente seu raciocínio sem ter feito uso da linguagem matemática formal, aceite sem interferências. Deixe que as formalizações sejam feitas no momento oportuno, ao final da aula, na etapa de Sistematização do Conceito. Para isto, utilize o material das dicas para o professor para organizar a linguagem e uso correto dos termos envolvidos na resolução. Peça aos alunos que registrem os diferentes raciocínios que tiveram no caderno. Se tiver um projetor à sua disposição, apresente os slides como apoio à sua explicação.
Propósito: Mostrar aos alunos a aplicabilidade do valor numérico de uma expressão algébrica em uma situação-problema que envolve a medição e comparação de medidas de lotes de terrenos.
Sistematização do Conceito
Tempo sugerido: 5 minutos.
Orientações: Encerrada a apresentação da(s) solução(ões), apresente o conceito formal da aula. Veja que propositalmente, há a inversão da apresentação do conceito (que no modelo tradicional, acontece no início da aula). Isto dará mais significado e sentido à aprendizagem do aluno.
Propósito: Definir, formalmente, o conceito matemático de valor numérico de uma expressão algébrica.
Encerramento
Tempo sugerido: 2 minutos.
Orientações: Esta é uma parte que se apresenta a síntese do que foi aprendido durante a aula.
Propósito: Sintetizar os conceitos aprendidos e discutidos durante a aula.
Raio X
Tempo sugerido: 6 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem no caderno. Circule pela sala e verifique como os alunos estão realizando a escrita da expressão algébrica e o valor numérico para o perímetro do terreno. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos em uma outra situação e avaliar os conhecimentos de cada um a respeito do cálculo do valor numérico.
Materiais Complementares:
