Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Para acessar documento com sugestões de Referências Bibliográficas, clique aqui.
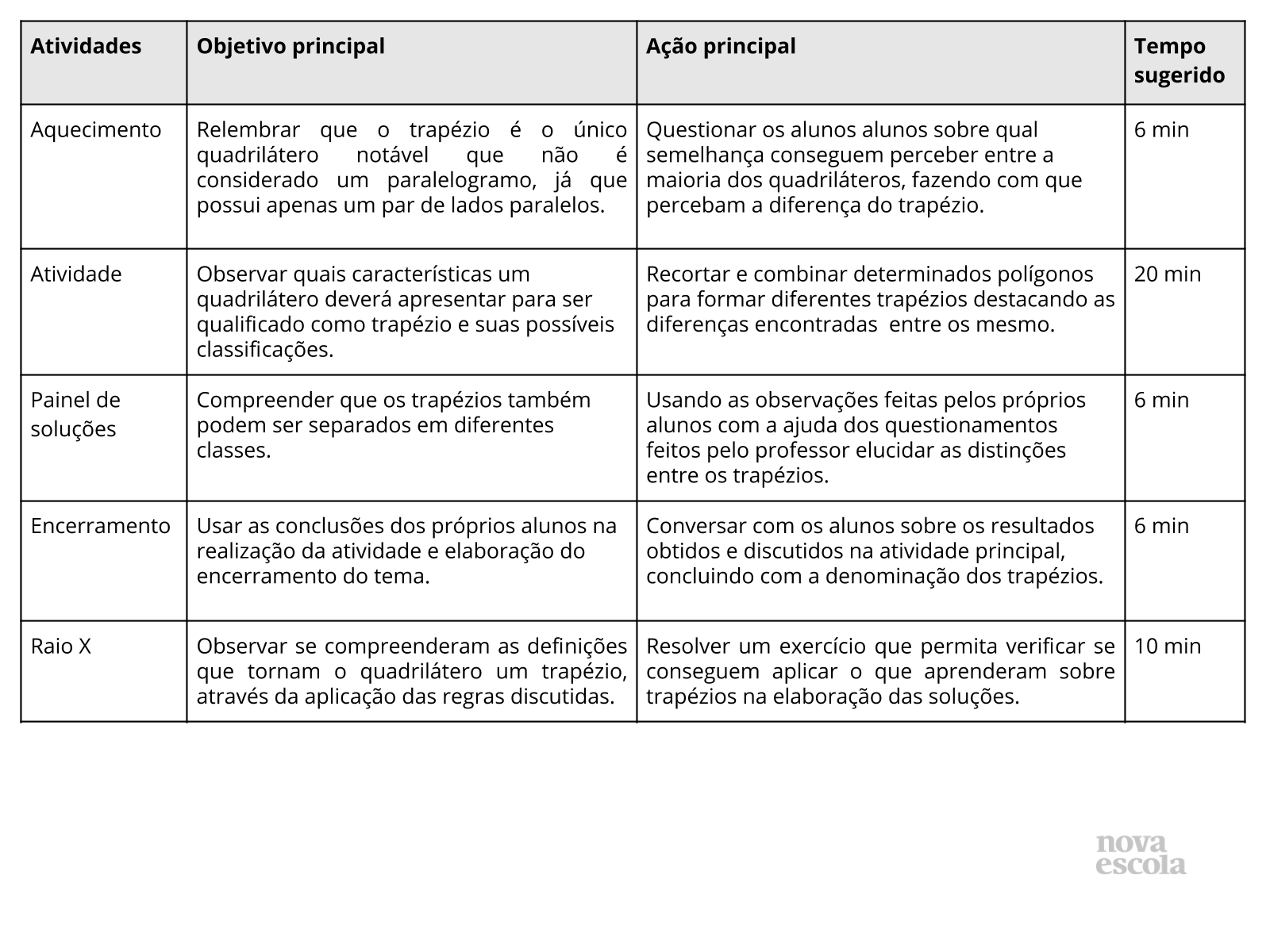
Aquecimento

Tempo sugerido: 6 minutos
Orientações: Questione os alunos sobre os quadriláteros que conseguem se lembrar. Peça que descrevam o quadrilátero lembrado e desenhem o mesmo na lousa. Se nenhum aluno citar o trapézio, desenhe um na lousa mas não comente suas características.
Pergunte aos alunos:
- Qual é a principal semelhança entre a maioria dos quadriláteros desenhados?
- Dos quadriláteros desenhados podemos perceber uma característica única em algum deles?
Propósito: Relembrar que o trapézio é o único quadrilátero notável que não é considerado um paralelogramo, já que possui apenas um par de lados paralelos.
Materiais complementares para impressão:
Aquecimento
Atividade principal
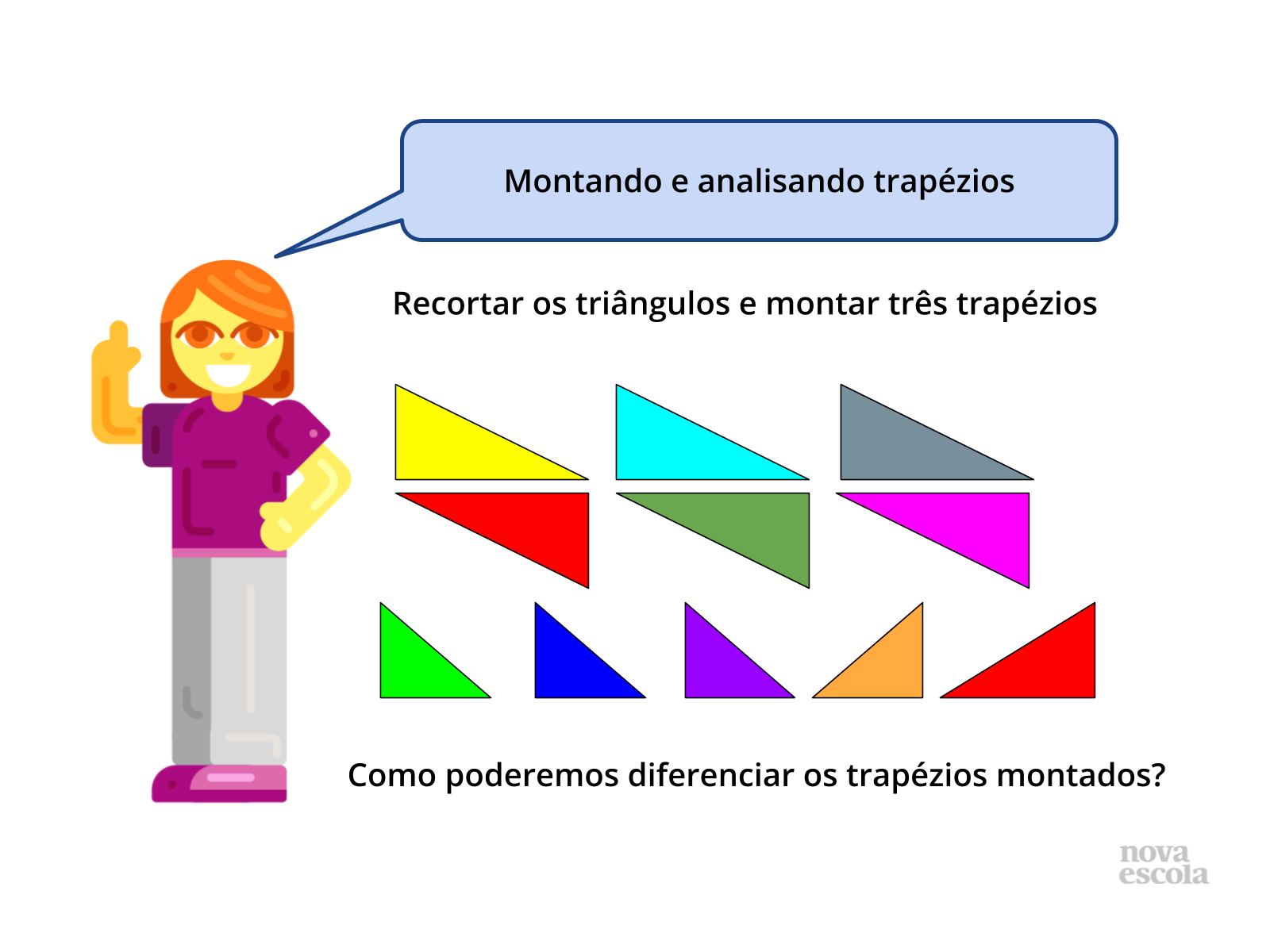
Tempo sugerido: 20 minutos
Orientações: Diga aos alunos para que juntem as carteiras e formarem grupos. Distribua uma folha com os triângulos para cada grupo (figuras coloridas ou preto e branco, a escolha do professor), uma folha sulfite em branco, uma régua, uma tesoura e uma cola. Explique que deverão recortar os triângulos (explique aos alunos que são todos triângulos retângulos) e combiná-los de maneira que formem trapézios (três no total), feito isso diga que deverão encontrar maneiras de diferenciar os trapézios montados, escrevendo essas diferenças em baixo do trapézio criado. Incentive os grupos a observarem os trapézios feitos por outros grupos.
Converse com os alunos:
- O que todos os trapézios têm em comum? (R: 1 par de lados paralelos, por isso não são paralelogramos)
- Qual a quantidade mínima de triângulos usados para criar um trapézio? (R: 3)
- Todos os trapézios possuem a mesma quantidade de lados apesar de terem sido formados por mais de 3 triângulos? (R: Sim, pois todos os trapézios são quadriláteros)
- Os trapézios que meu grupo montou são iguais a de todos os outros grupos? (R: Cada grupo deve perceber as desigualdades entre os trapézios feitos pelos grupos)
- Quais são as diferenças entre os trapézios que construímos? (R: Os grupos deverão elencar as diferenças percebidas)
Propósito: Compreender que os trapézios poderão ser diferenciados de acordo com a medida de seus lados e ângulos.
Materiais complementares para impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de intervenção
Analisando as soluções

Tempo sugerido: 6 minutos (slides 5 e 6)
Orientações: Como a atividade admite diversas combinações será melhor que os grupos apresentem para seus colegas os trapézios que conseguiram montar juntamente com as observações sobre como diferenciaram os trapézios feitos.
Exemplos de questionamentos que podem ser feitos aos grupos durante sua apresentação:
- Os lados não paralelos dos trapézios são sempre diferentes?
- Dentre os trapézios montados, algum possui ângulo reto? Somente 1 ângulo reto? Por quê?
- Como seu grupo separaria os trapézios feitos?
Propósito: Através das respostas dos próprios alunos fazer com que percebam as características que definirão os tipos de trapézios (todos os lados diferentes, lados não paralelos iguais e ângulos retos).
Analisando as soluções
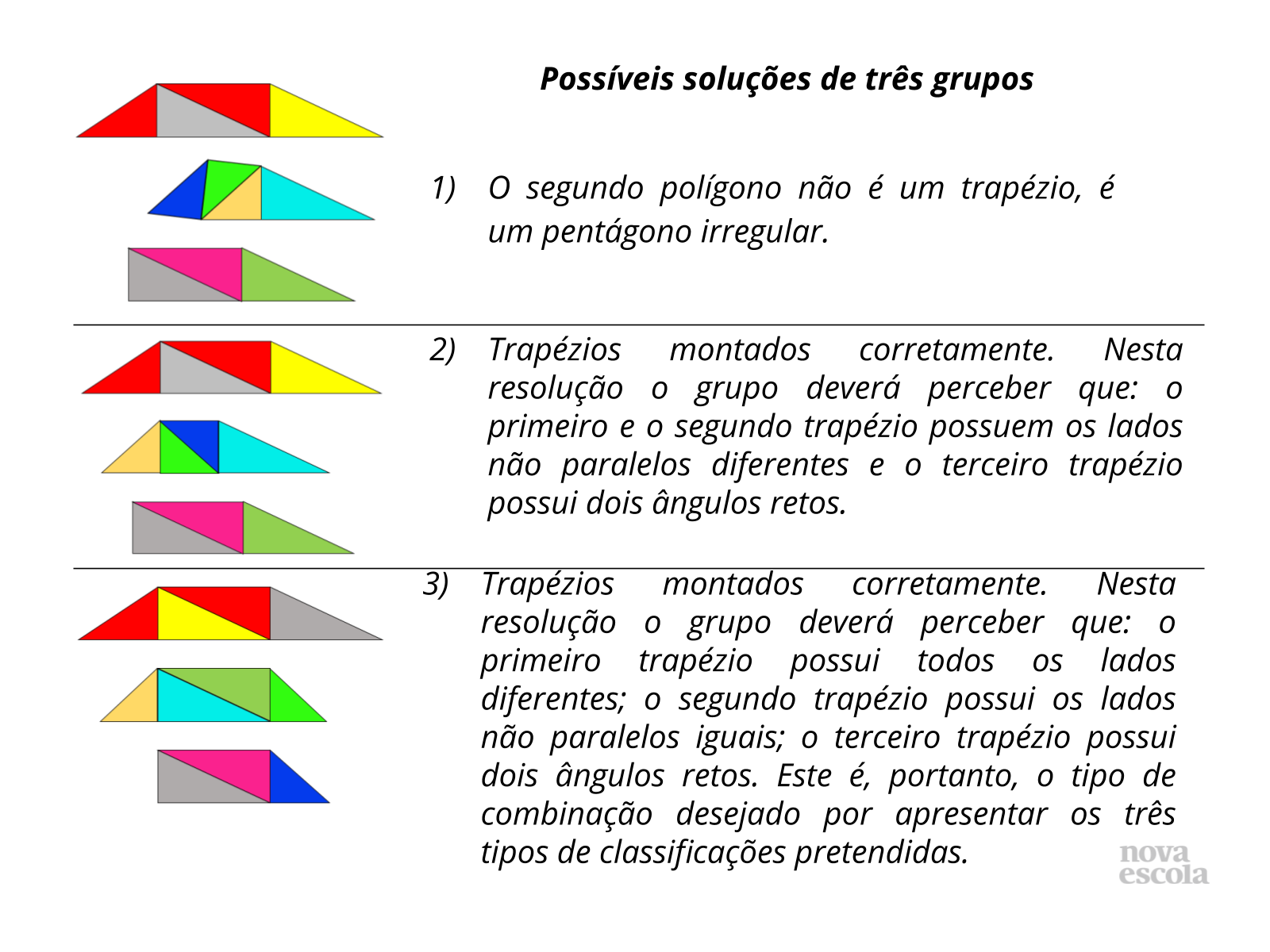
Tempo sugerido: 6 minutos (slides 5 e 6)
Orientações: Como a atividade admite diversas combinações será melhor que os grupos apresentem para seus colegas os trapézios que conseguiram montar juntamente com as observações sobre como diferenciaram os trapézios feitos.
Exemplos de questionamentos que podem ser feitos aos grupos durante sua apresentação:
- Os lados não paralelos dos trapézios são sempre diferentes?
- Dentre os trapézios montados, algum possui ângulo reto? Somente 1 ângulo reto? Por quê?
- Como seu grupo separaria os trapézios feitos?
Propósito: Através das respostas dos próprios alunos fazer com que percebam as características que definirão os tipos de trapézios (todos os lados diferentes, lados não paralelos iguais e ângulos retos).
Encerramento

Tempo sugerido: 6 minutos
Orientações: Converse novamente com os alunos sobre as observações feitas pelos mesmos durante o decorrer da aula. Conclua a aula com a denominação de cada trapézio:
- Trapézios com todos os lados diferentes são denominados escalenos;
- Trapézios com os dois lados não paralelos congruentes* são denominados isósceles;
- Trapézios com dois ângulos retos são denominados retângulos.
*Explicar a diferença entre igual e congruente:
Congruente
Peça para escreverem em seus cadernos o que aprenderam na aula.
Propósito: Compreender que os trapézios além de serem diferentes dos demais quadriláteros (não são paralelogramos) também possuem distinções que os separam em classes.