Atividade principal
Plano de Aula
Plano de aula: Conversão de Medidas de Comprimento em Metro
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Unidades de medida para distâncias muito curtas ou muito longas
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Fábio Leandro Cruzado
Mentor: Emiliano Augusto Chagas
Especialista de área: Fernando Barnabé
Habilidade da BNCC
EF09MA18 - Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas, tais como distância entre planetas e sistemas solares, tamanho de vírus ou de células, capacidade de armazenamento de computadores, entre outros.
Objetivos específicos
Converter unidades de medidas de comprimento (muito longas ou muito curtas) em metro.
Conceito-chave
Múltiplos e Submúltiplos do metro.
Conhecimentos que a turma deve dominar
Conhecer os múltiplos e os submúltiplos do metro.
Efetuar divisões e multiplicações por 10, 100, 1000, ou seja, efetuar cálculos envolvendo potências de base 10.
Conhecer o significado de cada algarismos nos números do sistema de numeração posicional (base 10).
Resolver problemas utilizando Regra de Três Simples.
Recursos necessários
- Atividades impressas em folhas, lápis, borracha.
Habilidades BNCC:
Objetivos de aprendizagem
Converter unidades de medidas de comprimento (muito longas ou muito curtas) em metro.
Resumo da aula
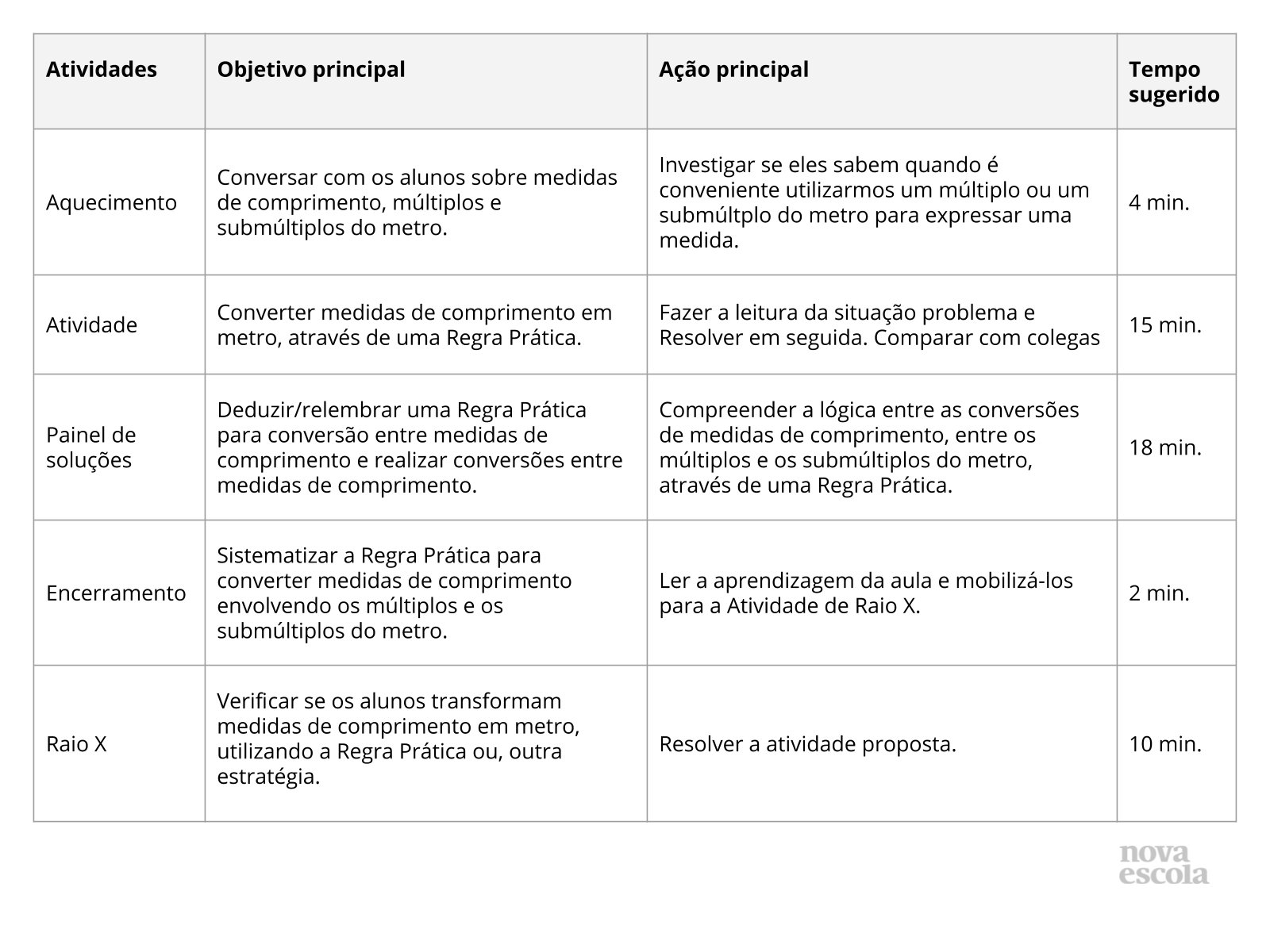
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 1 minuto.
Orientação: Projete ou escreva o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula, criando uma boa expectativa em relação ao que irão aprender durante a aula.
Aquecimento

Tempo previsto: 4 minutos.
Orientações: Prepare as atividades (principal, raio X e complementares) antes da aula. Se possível, traga essas atividades impressas para os alunos, ou projete-as na lousa. Converse com seus alunos sobre os múltiplos e submúltiplos do metro. Questione-os se eles sabem porque o metro é a unidade padrão para medidas de comprimento no mundo inteiro. Questione-os se eles sabem o significado de SI - Sistema Internacional de Unidades. Questione-os se eles conhecem outras medidas pertencentes ao SI. Questione-os sobre os significados dos múltiplos e dos submúltiplos do metro, e seus respectivos valores. Questione-os sobre a melhor medida de comprimento a ser adotada para medir uma caneta, o comprimento da lousa, e a distância entre suas casas até a escola. Esses questionamentos darão um bom norte do conhecimento prévio que os alunos possuem sobre o assunto abordado na Atividade Principal.
Propósito: Realizar, através de questões direcionadas, um levantamento dos conhecimentos prévios que os alunos possuem sobre o tema e, motivá-los a utilizar esse conhecimento para resolver a situação problema proposta.
Discuta com a turma:
- Quais são os múltiplos do metro?
- Quais são os submúltiplos do metro?
- Qual o significado de “ser múltiplo de”?
- Qual o significado de “ser submúltiplo de”?
- Quais os valores, em metros, dos múltiplos do metro?
- Quais os valores, em metro, dos submúltiplos do metro?
- O que devemos usar para expressar o comprimento de uma caneta, um múltiplo ou um submúltiplo do metro?
- O que devemos usar para expressar o comprimento de uma lousa, um múltiplo ou um submúltiplo do metro?
- O que devemos usar para expressar a distância entre a casa de vocês até a escola, um múltiplo ou um submúltiplo do metro?
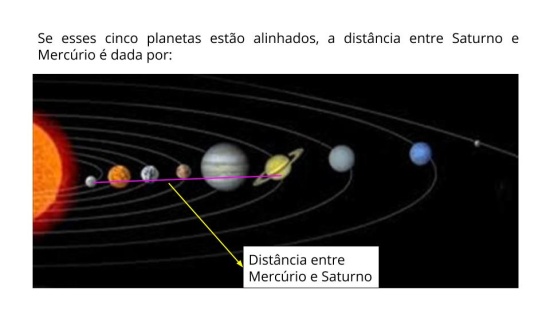
Atividade principal

Tempo sugerido: 15 minutos (Slides 4 a 8).
Orientações: Divida os alunos em duplas. Agrupe alunos com níveis de proficiências próximos (não iguais) para que um ajude o outro. Solicite que os alunos façam a leitura e análise do problema individualmente nas duplas. Nesse momento, as duplas já podem trocar informações/ideias de resolução e conhecimentos prévios que eles possuem. Solicite que eles grifem/destaquem no texto do problema, palavras-chaves que auxiliarão na resolução dos itens, e tentem resolver o problema. Permeie entre as carteiras e observe se algum aluno não está realizando a atividade. Aproveite esse momento para intervir e fazer registros das dificuldades que forem surgindo. No momento da socialização do problema, procure abordar (sem expor os alunos) essa(s) dificuldade(s). Após isso, peça que comparem suas soluções com as de outros colegas. Escolha um aluno/dupla para socializar as respostas de cada item do problema.
Propósito: Fazer com que os alunos deduzam uma regra prática para conversão entre medidas de comprimento, utilizando os múltiplos e os submúltiplos do metro, dando significado aos seus nomes e aos seus respectivos valores.
Materiais complementares para impressão:
Atividade principal
Tempo sugerido: 15 minutos (Slides 4 a 8).
Orientações: Divida os alunos em duplas. Agrupe alunos com níveis de proficiências próximos (não iguais) para que um ajude o outro. Solicite que os alunos façam a leitura e análise do problema individualmente nas duplas. Nesse momento, as duplas já podem trocar informações/ideias de resolução e conhecimentos prévios que eles possuem. Solicite que eles grifem/destaquem no texto do problema, palavras-chaves que auxiliarão na resolução dos itens, e tentem resolver o problema. Permeie entre as carteiras e observe se algum aluno não está realizando a atividade. Aproveite esse momento para intervir e fazer registros das dificuldades que forem surgindo. No momento da socialização do problema, procure abordar (sem expor os alunos) essa(s) dificuldade(s). Após isso, peça que comparem suas soluções com as de outros colegas. Escolha um aluno/dupla para socializar as respostas de cada item do problema.
Propósito: Fazer com que os alunos deduzam uma regra prática para conversão entre medidas de comprimento, utilizando os múltiplos e os submúltiplos do metro, dando significado aos seus nomes e aos seus respectivos valores.
Atividade principal

Tempo sugerido: 15 minutos (Slides 4 a 8).
Orientações: Divida os alunos em duplas. Agrupe alunos com níveis de proficiências próximos (não iguais) para que um ajude o outro. Solicite que os alunos façam a leitura e análise do problema individualmente nas duplas. Nesse momento, as duplas já podem trocar informações/ideias de resolução e conhecimentos prévios que eles possuem. Solicite que eles grifem/destaquem no texto do problema, palavras-chaves que auxiliarão na resolução dos itens, e tentem resolver o problema. Permeie entre as carteiras e observe se algum aluno não está realizando a atividade. Aproveite esse momento para intervir e fazer registros das dificuldades que forem surgindo. No momento da socialização do problema, procure abordar (sem expor os alunos) essa(s) dificuldade(s). Após isso, peça que comparem suas soluções com as de outros colegas. Escolha um aluno/dupla para socializar as respostas de cada item do problema.
Propósito: Fazer com que os alunos deduzam uma regra prática para conversão entre medidas de comprimento, utilizando os múltiplos e os submúltiplos do metro, dando significado aos seus nomes e aos seus respectivos valores.
Atividade principal

Tempo sugerido: 15 minutos (Slides 4 a 8).
Orientações: Divida os alunos em duplas. Agrupe alunos com níveis de proficiências próximos (não iguais) para que um ajude o outro. Solicite que os alunos façam a leitura e análise do problema individualmente nas duplas. Nesse momento, as duplas já podem trocar informações/ideias de resolução e conhecimentos prévios que eles possuem. Solicite que eles grifem/destaquem no texto do problema, palavras-chaves que auxiliarão na resolução dos itens, e tentem resolver o problema. Permeie entre as carteiras e observe se algum aluno não está realizando a atividade. Aproveite esse momento para intervir e fazer registros das dificuldades que forem surgindo. No momento da socialização do problema, procure abordar (sem expor os alunos) essa(s) dificuldade(s). Após isso, peça que comparem suas soluções com as de outros colegas. Escolha um aluno/dupla para socializar as respostas de cada item do problema.
Propósito: Fazer com que os alunos deduzam uma regra prática para conversão entre medidas de comprimento, utilizando os múltiplos e os submúltiplos do metro, dando significado aos seus nomes e aos seus respectivos valores.
Atividade principal

Tempo sugerido: 15 minutos (Slides 4 a 8).
Orientações: Divida os alunos em duplas. Agrupe alunos com níveis de proficiências próximos (não iguais) para que um ajude o outro. Solicite que os alunos façam a leitura e análise do problema individualmente nas duplas. Nesse momento, as duplas já podem trocar informações/ideias de resolução e conhecimentos prévios que eles possuem. Solicite que eles grifem/destaquem no texto do problema, palavras-chaves que auxiliarão na resolução dos itens, e tentem resolver o problema. Permeie entre as carteiras e observe se algum aluno não está realizando a atividade. Aproveite esse momento para intervir e fazer registros das dificuldades que forem surgindo. No momento da socialização do problema, procure abordar (sem expor os alunos) essa(s) dificuldade(s). Após isso, peça que comparem suas soluções com as de outros colegas. Escolha um aluno/dupla para socializar as respostas de cada item do problema.
Propósito: Fazer com que os alunos deduzam uma regra prática para conversão entre medidas de comprimento, utilizando os múltiplos e os submúltiplos do metro, dando significado aos seus nomes e aos seus respectivos valores.
Discussão de soluções
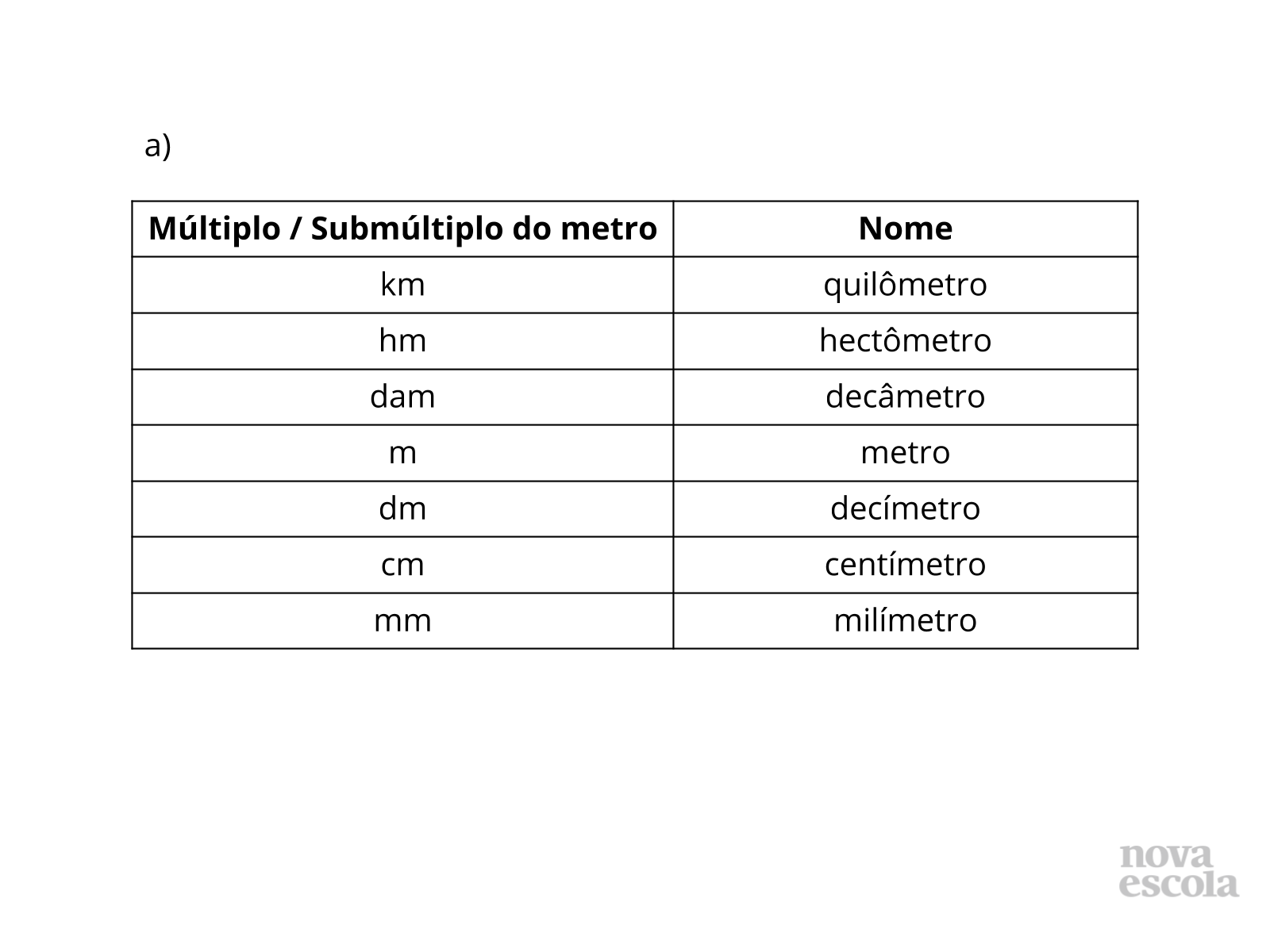
Tempo sugerido: 15 minutos. (Slides 9 a 16)
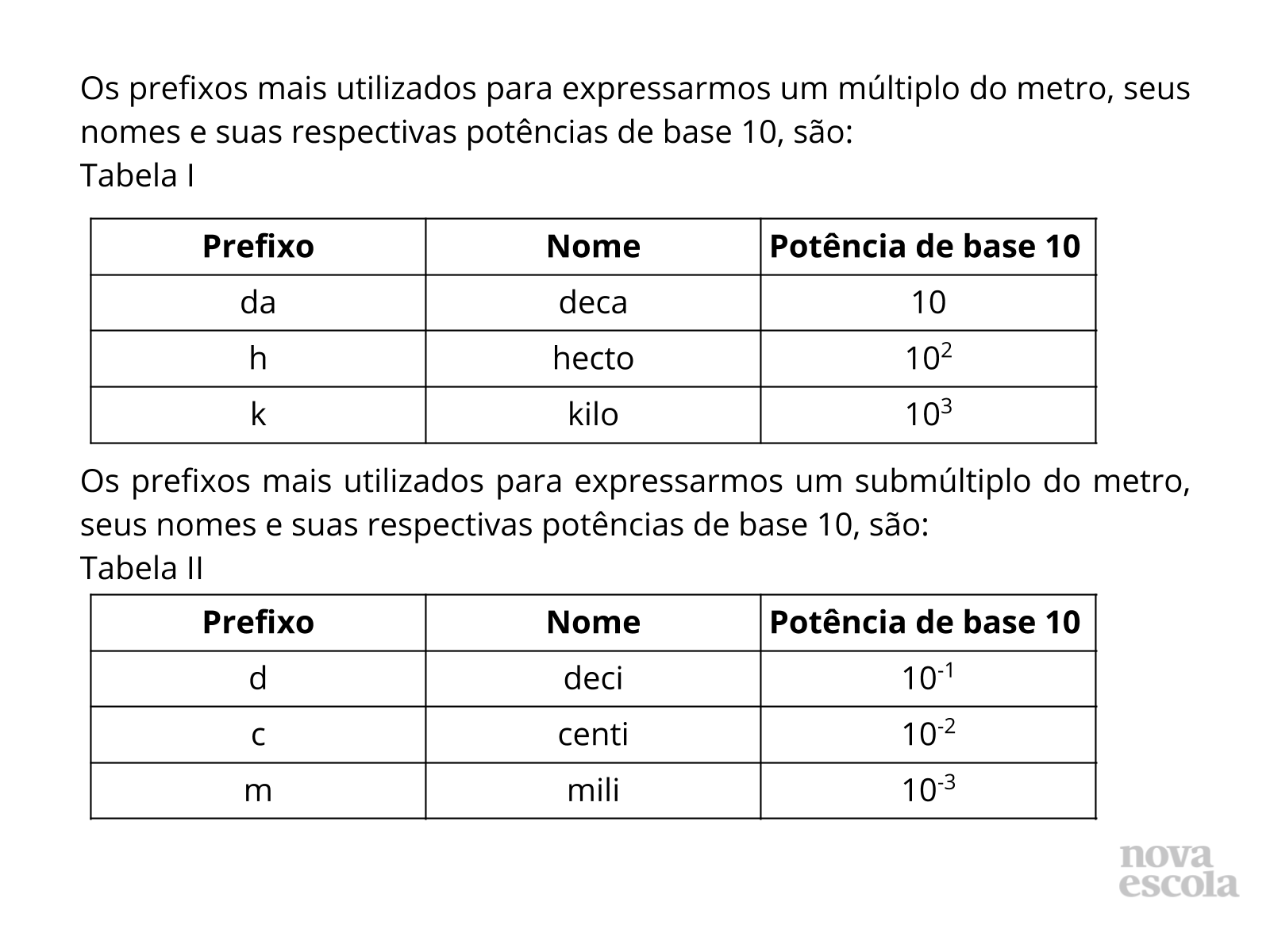
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides (slides de 9 a 16) destacando algumas possíveis soluções dos itens do problema. No item a), temos uma excelente oportunidade para os alunos relembrarem e organizarem na ordem os nomes dos múltiplos e dos submúltiplos do metro. Professor, durante a socialização deste item, questione-os sobre o significado de kilo (ou quilo), hecto, deca, deci, centi, mili… alguns desses prefixos são mais utilizados no nosso cotidiano que outros, porém, é muito importante que os alunos conheçam o significado desses prefixos, associando-os, se possível, com os valores das suas respectivas potências de base 10. Esses prefixos serão (ou já foram) utilizados em outras unidades de medidas, como volume (capacidade), por exemplo.
Propósito: Familiarizar os alunos com os nomes dos múltiplos e dos submúltiplos do metro, dando significado aos seus prefixos, relacionando-os com seus respectivos valores.
Discuta com a turma:
- Quais são os múltiplos do metro?
- Quais são os submúltiplos do metro?
- Qual o significado de kilo?
- Qual o significado de centi?
- Qual o significado de mili?
...entre outras questões análogas a essas.
Discussão de soluções

Tempo sugerido: 15 minutos. (Slides 9 a 16)
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides (slides de 9 a 16) destacando algumas possíveis soluções dos itens do problema.
No item b), vamos descrever todas (ou quase todas) as observações que podemos ter em relação a essa tabela (Tabela III) e assim, conduzir o nosso raciocínio a uma Regra Prática para conversão entre medidas de comprimento. A resolução deste item é bem extensa, porém, é importante fazer uma análise com bastante atenção da mesma, uma vez que essa explanação revela as explicações da funcionalidade da Regra Prática de conversão entre as medidas de comprimento.
Discuta também, o significado dos prefixos deca, hecto e kilo, que representam respectivamente, 10 vezes, 100 vezes e mil vezes. Isso ajudará a tornar mais significativos os nomes dos múltiplos do metro e seus respectivos valores.
Professor, discuta com seus alunos que 1 = 1,0, ou 1 = 1,00, ou 10 = 10,0, ou 10 = 10,00, …, pois certamente vai causar estranheza deslocar algo que não é visível. É importante que você insista em convencer seu aluno quanto a esse acontecimento, isso tornará mais significativo quando a medida dada inicialmente for um número decimal.
Discuta também o significado dos prefixos deci, centi e mili, que representam respectivamente, décimo de alguma coisa, centésimo de alguma coisa e milésimo de alguma coisa, ou ainda, 10 vezes menor, 100 vezes menor, 1000 vezes menor. Isso ajudará a tornar mais significativos os nomes dos submúltiplos do metro e seus respectivos valores.
Propósito: Deduzir uma regra para conversão entre medidas de comprimento, dando significado aos passos realizados.
Discuta com a turma:
- Quando multiplicamos um número por 10, o que ocorre com o resultado quando comparado ao número original?
- Quando multiplicamos um número por 100, o que ocorre com o resultado quando comparado ao número original?
- Quando multiplicamos um número por 1000, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 10, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 100, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 1000, o que ocorre com o resultado quando comparado ao número original?
- É possível prever o resultado de uma multiplicação por 10, 100, 1000, sem realizá-la? E o resultado de uma divisão por 10, 100, 1000, é possível prevê-lo? Porquê?
Discussão de soluções

Tempo sugerido: 15 minutos. (Slides 9 a 16)
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides (slides de 9 a 16) destacando algumas possíveis soluções dos itens do problema.
No item b), vamos descrever todas (ou quase todas) as observações que podemos ter em relação a essa tabela (Tabela III) e assim, conduzir o nosso raciocínio a uma Regra Prática para conversão entre medidas de comprimento. A resolução deste item é bem extensa, porém, é importante fazer uma análise com bastante atenção da mesma, uma vez que essa explanação revela as explicações da funcionalidade da Regra Prática de conversão entre as medidas de comprimento.
Discuta também, o significado dos prefixos deca, hecto e kilo, que representam respectivamente, 10 vezes, 100 vezes e mil vezes. Isso ajudará a tornar mais significativos os nomes dos múltiplos do metro e seus respectivos valores.
Professor, discuta com seus alunos que 1 = 1,0, ou 1 = 1,00, ou 10 = 10,0, ou 10 = 10,00, …, pois certamente vai causar estranheza deslocar algo que não é visível. É importante que você insista em convencer seu aluno quanto a esse acontecimento, isso tornará mais significativo quando a medida dada inicialmente for um número decimal.
Discuta também o significado dos prefixos deci, centi e mili, que representam respectivamente, décimo de alguma coisa, centésimo de alguma coisa e milésimo de alguma coisa, ou ainda, 10 vezes menor, 100 vezes menor, 1000 vezes menor. Isso ajudará a tornar mais significativos os nomes dos submúltiplos do metro e seus respectivos valores.
Propósito: Deduzir uma regra para conversão entre medidas de comprimento, dando significado aos passos realizados.
Discuta com a turma:
- Quando multiplicamos um número por 10, o que ocorre com o resultado quando comparado ao número original?
- Quando multiplicamos um número por 100, o que ocorre com o resultado quando comparado ao número original?
- Quando multiplicamos um número por 1000, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 10, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 100, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 1000, o que ocorre com o resultado quando comparado ao número original?
- É possível prever o resultado de uma multiplicação por 10, 100, 1000, sem realizá-la? E o resultado de uma divisão por 10, 100, 1000, é possível prevê-lo? Porquê?
Discussão de soluções

Tempo sugerido: 15 minutos. (Slides 9 a 16)
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides (slides de 9 a 16) destacando algumas possíveis soluções dos itens do problema.
No item b), vamos descrever todas (ou quase todas) as observações que podemos ter em relação a essa tabela (Tabela III) e assim, conduzir o nosso raciocínio a uma Regra Prática para conversão entre medidas de comprimento. A resolução deste item é bem extensa, porém, é importante fazer uma análise com bastante atenção da mesma, uma vez que essa explanação revela as explicações da funcionalidade da Regra Prática de conversão entre as medidas de comprimento.
Discuta também, o significado dos prefixos deca, hecto e kilo, que representam respectivamente, 10 vezes, 100 vezes e mil vezes. Isso ajudará a tornar mais significativos os nomes dos múltiplos do metro e seus respectivos valores.
Professor, discuta com seus alunos que 1 = 1,0, ou 1 = 1,00, ou 10 = 10,0, ou 10 = 10,00, …, pois certamente vai causar estranheza deslocar algo que não é visível. É importante que você insista em convencer seu aluno quanto a esse acontecimento, isso tornará mais significativo quando a medida dada inicialmente for um número decimal.
Discuta também o significado dos prefixos deci, centi e mili, que representam respectivamente, décimo de alguma coisa, centésimo de alguma coisa e milésimo de alguma coisa, ou ainda, 10 vezes menor, 100 vezes menor, 1000 vezes menor. Isso ajudará a tornar mais significativos os nomes dos submúltiplos do metro e seus respectivos valores.
Propósito: Deduzir uma regra para conversão entre medidas de comprimento, dando significado aos passos realizados.
Discuta com a turma:
- Quando multiplicamos um número por 10, o que ocorre com o resultado quando comparado ao número original?
- Quando multiplicamos um número por 100, o que ocorre com o resultado quando comparado ao número original?
- Quando multiplicamos um número por 1000, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 10, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 100, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 1000, o que ocorre com o resultado quando comparado ao número original?
- É possível prever o resultado de uma multiplicação por 10, 100, 1000, sem realizá-la? E o resultado de uma divisão por 10, 100, 1000, é possível prevê-lo? Porquê?
Discussão de soluções

Tempo sugerido: 15 minutos. (Slides 9 a 16)
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides (slides de 9 a 16) destacando algumas possíveis soluções dos itens do problema.
No item b), vamos descrever todas (ou quase todas) as observações que podemos ter em relação a essa tabela (Tabela III) e assim, conduzir o nosso raciocínio a uma Regra Prática para conversão entre medidas de comprimento. A resolução deste item é bem extensa, porém, é importante fazer uma análise com bastante atenção da mesma, uma vez que essa explanação revela as explicações da funcionalidade da Regra Prática de conversão entre as medidas de comprimento.
Discuta também, o significado dos prefixos deca, hecto e kilo, que representam respectivamente, 10 vezes, 100 vezes e mil vezes. Isso ajudará a tornar mais significativos os nomes dos múltiplos do metro e seus respectivos valores.
Professor, discuta com seus alunos que 1 = 1,0, ou 1 = 1,00, ou 10 = 10,0, ou 10 = 10,00, …, pois certamente vai causar estranheza deslocar algo que não é visível. É importante que você insista em convencer seu aluno quanto a esse acontecimento, isso tornará mais significativo quando a medida dada inicialmente for um número decimal.
Discuta também o significado dos prefixos deci, centi e mili, que representam respectivamente, décimo de alguma coisa, centésimo de alguma coisa e milésimo de alguma coisa, ou ainda, 10 vezes menor, 100 vezes menor, 1000 vezes menor. Isso ajudará a tornar mais significativos os nomes dos submúltiplos do metro e seus respectivos valores.
Propósito: Deduzir uma regra para conversão entre medidas de comprimento, dando significado aos passos realizados.
Discuta com a turma:
- Quando multiplicamos um número por 10, o que ocorre com o resultado quando comparado ao número original?
- Quando multiplicamos um número por 100, o que ocorre com o resultado quando comparado ao número original?
- Quando multiplicamos um número por 1000, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 10, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 100, o que ocorre com o resultado quando comparado ao número original?
- Quando dividimos um número por 1000, o que ocorre com o resultado quando comparado ao número original?
- É possível prever o resultado de uma multiplicação por 10, 100, 1000, sem realizá-la? E o resultado de uma divisão por 10, 100, 1000, é possível prevê-lo? Porquê?
Discussão de soluções

Tempo sugerido: 15 minutos. (Slides 9 a 16)
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides (slides de 9 a 16) destacando algumas possíveis soluções dos itens do problema.
No item c), vamos abordar uma conversão entre medidas dadas em decímetro para kilômetro. Professor, note que existem pelo menos duas resoluções deste item, explore essas duas estratégias com seus alunos. Verifique se algum aluno resolveu este item utilizando uma outra estratégia diferente dessas. Caso isso ocorra, socialize-a com a classe.
Propósito: Aplicar a regra prática, ou outro artifício de cálculo, para converter uma medida de comprimento inicialmente dada em dm para km.
Discuta com a turma:
- Quantos “pulos” devemos dar para sair do m e chegam em km? Esses “pulos” são para esquerda ou direita?
- Segundo a regra, devemos dividir uma medida dada em m por quanto para convertê-la em km? Existe alguma associação deste raciocínio com os “pulos” que devemos dar para sair do m e chegar em km?
Discussão de soluções

Tempo sugerido: 15 minutos. (Slides 9 a 16)
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides (slides de 9 a 16) destacando algumas possíveis soluções dos itens do problema.
No item d), temos uma situação análoga ao item c), por isso devemos utilizar os mesmos passos. Professor, note que existem pelo menos duas resoluções deste item, explore essas duas estratégias com seus alunos. Verifique se algum aluno resolveu este item utilizando uma outra estratégia diferente dessas. Caso isso ocorra, socialize-a com a classe.
Propósito: Aplicar a regra prática, ou outro artifício de cálculo para converter uma medida de comprimento inicialmente dada em km para mm.
Discuta com a turma:
- Quantos “pulos” devemos dar para sair do m e chegam em mm? Esses “pulos” são para esquerda ou direita?
- Segundo a regra, devemos multiplicar uma medida dada em m por quanto para convertê-la em mm? Existe alguma associação deste raciocínio com os “pulos” que devemos dar para sair do km e chegar em mm?
Discussão de soluções

Tempo sugerido: 15 minutos. (Slides 9 a 16)
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides (slides de 9 a 16) destacando algumas possíveis soluções dos itens do problema.
No item e), temos uma situação análoga aos itens c) e d), por isso, devemos utilizar os mesmos passos. Professor, novamente, note que existem pelo menos duas resoluções deste item, explore essas duas estratégias com seus alunos. Verifique se algum aluno resolveu este item utilizando uma outra estratégia diferente dessas. Caso isso ocorra, socialize-a com a classe. Converse com seus alunos que a polegada é também muito utilizada no nosso cotidiano, e que é importante termos em mente o seu valor em centímetros.
Propósito: Aplicar a regra prática, ou outro artifício de cálculo para converter uma medida de comprimento inicialmente dada em cm para m e de cm para mm.
Discuta com a turma:
- Qual a unidade de comprimento que é utilizada medir a tela de uma TV ou de um celular?
- Como devemos medir o comprimento da tela de um celular? Caso eles desconheçam, pegue um celular com medida de tela conhecida na classe e meça, comparando o resultado com o real. Mostre que as telas de TVs e celulares em geral são medidas pela diagonal dos aparelhos.
Encerramento

Tempo sugerido: 3 minutos.
Orientações: Encerre a atividade retomando com os estudantes os múltiplos e os submúltiplos do metro, com seus respectivos significados. Mobilize-os para resolver a Atividade Raio X. Se possível, deixe a Regra Prática na lousa no momento da realização da Atividade de Raio X.
Propósito: Retomar a aprendizagem da aula.
Raio X
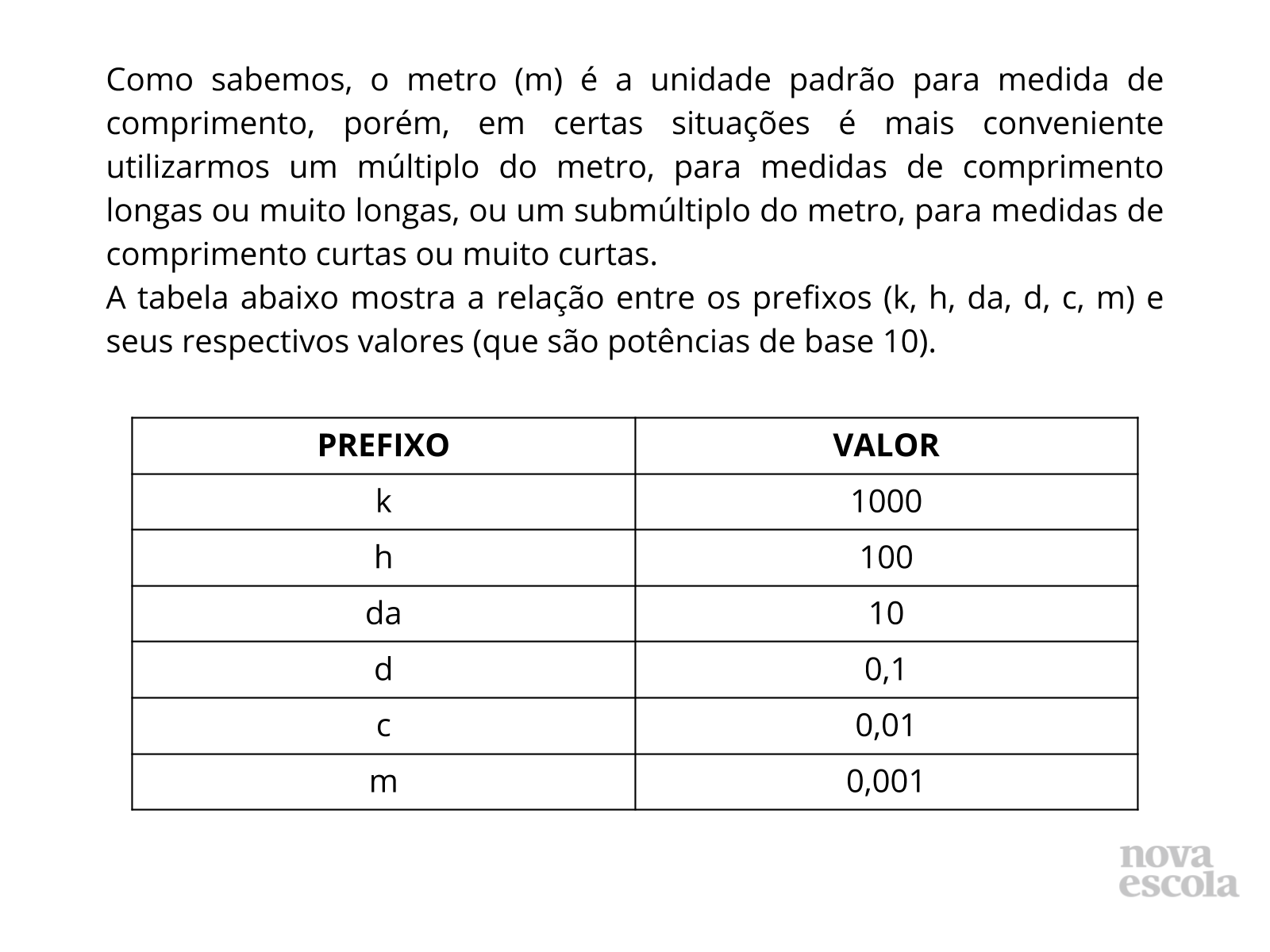
Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. É importante que todos os alunos tenham acesso às regras deduzidas e trabalhadas na Atividade Principal para poderem aplicar nessa atividade.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da conversão entre medidas de comprimento.
Materiais complementares para impressão:
Raio X
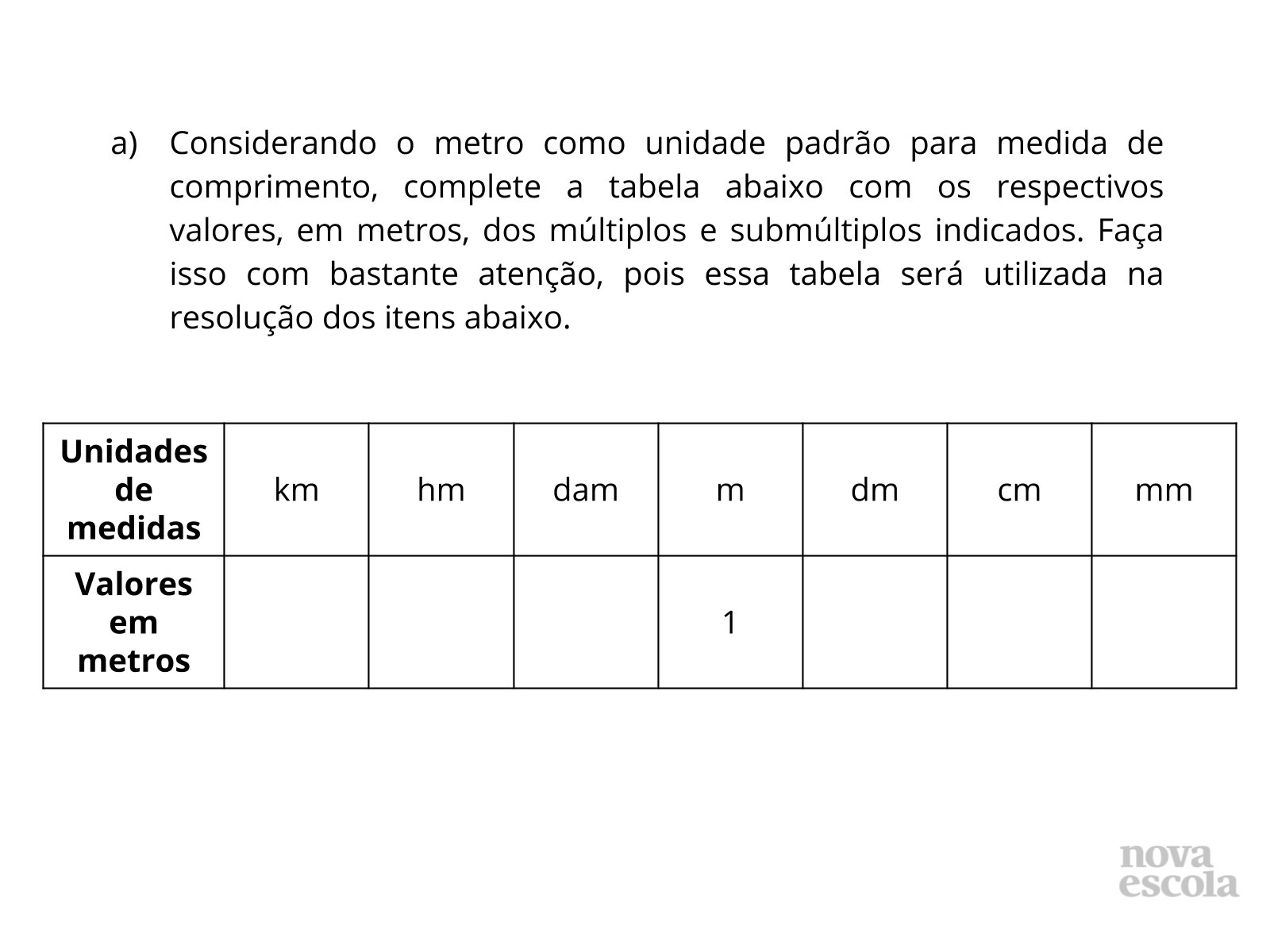
Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. É importante que todos os alunos tenham acesso às regras deduzidas e trabalhadas na Atividade Principal para poderem aplicar nessa atividade.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da conversão entre medidas de comprimento.
Raio X
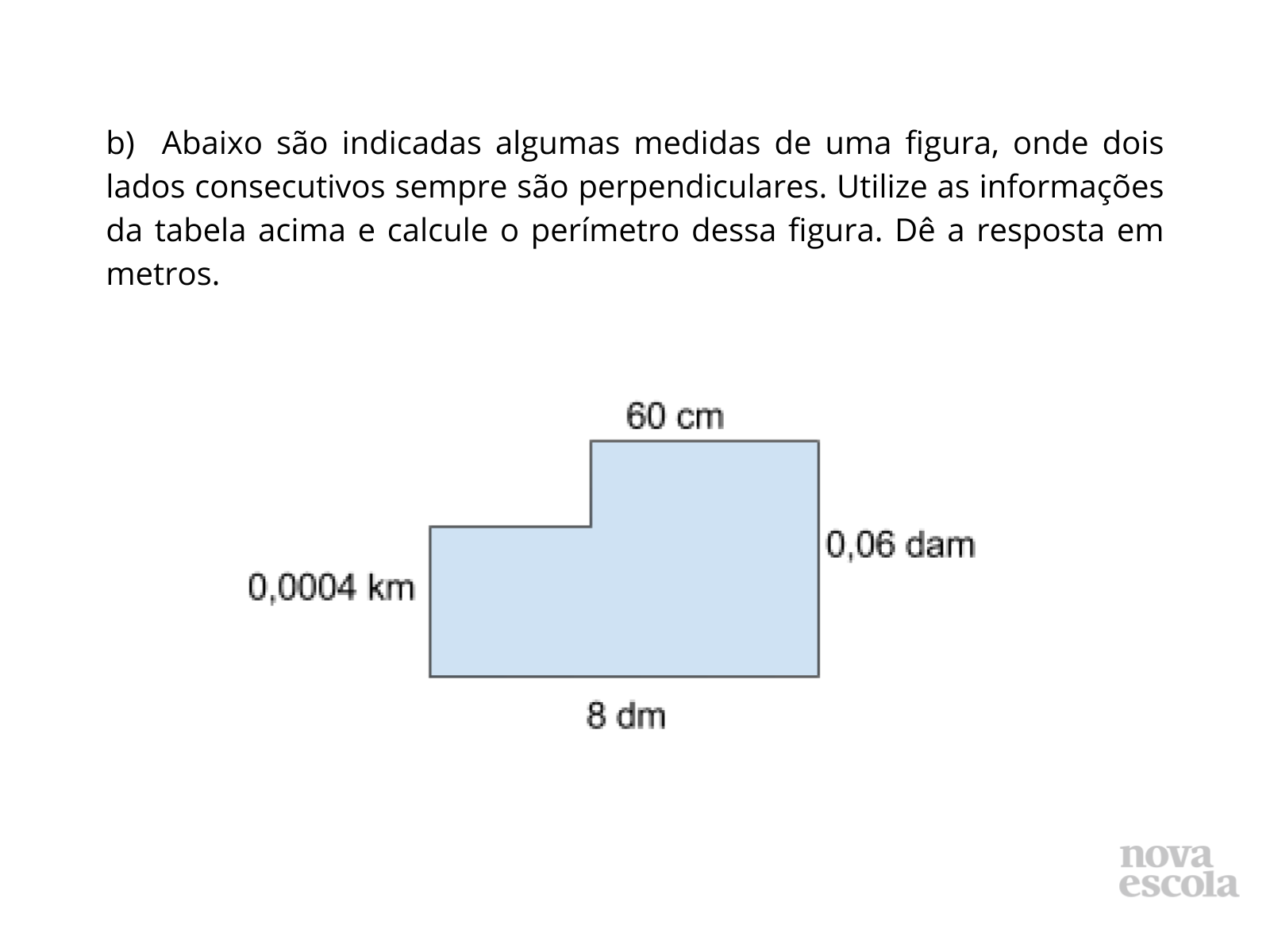
Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. É importante que todos os alunos tenham acesso às regras deduzidas e trabalhadas na Atividade Principal para poderem aplicar nessa atividade.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da conversão entre medidas de comprimento.
Raio X

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. É importante que todos os alunos tenham acesso às regras deduzidas e trabalhadas na Atividade Principal para poderem aplicar nessa atividade.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um a respeito da conversão entre medidas de comprimento.
Para o aluno
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_18GRM01)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) e papel para anotações.
- Optativas: Calculadora.
Aquecimento
Pela rede social escolhida, determine uma pesquisa rápida sobre a história do sistema internacional de unidades (SI) para perceberem os principais motivos para a existência de uma padronização.
Ainda antes de começar a atividade principal, é recomendável revisar rapidamente como se comportam as potências de base 10 com expoentes inteiros positivos e negativos.
Atividade principal
Para essa atividade, dê foco nos slides 7 e 8 que podem ser descritos facilmente ou você pode enviar uma imagem deles.
Discussão das soluções
A grande importância dessa aula está nas discussões das soluções, pois elas mostram os padrões de escrita, principalmente em relação à posição das vírgulas, e acréscimos e decréscimos de zeros.
Sistematização e encerramento
A sistematização e o encerramento aqui tem o foco de relembrar operações com potências de base 10 e como os padrões de escrita podem facilitar a conversão de unidades.
Raio X
Para esse raio X, sugira atividade de acesso aos links: https://www.convertworld.com/pt/
Ou
https://www.somatematica.com.br/softOnline/ConversorMedidas/conversor.php
E, nesse momento, façam experiências com conversão de unidades de distância.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas explorações sobre as novas experiências e o link acessado.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Fábio Leandro Cruzado
Mentor: Emiliano Augusto Chagas
Especialista de área: Fernando Barnabé
Habilidade da BNCC
EF09MA18 - Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas, tais como distância entre planetas e sistemas solares, tamanho de vírus ou de células, capacidade de armazenamento de computadores, entre outros.
Objetivos específicos
Converter unidades de medidas de comprimento (muito longas ou muito curtas) em metro.
Conceito-chave
Múltiplos e Submúltiplos do metro.
Conhecimentos que a turma deve dominar
Conhecer os múltiplos e os submúltiplos do metro.
Efetuar divisões e multiplicações por 10, 100, 1000, ou seja, efetuar cálculos envolvendo potências de base 10.
Conhecer o significado de cada algarismos nos números do sistema de numeração posicional (base 10).
Resolver problemas utilizando Regra de Três Simples.
Recursos necessários
- Atividades impressas em folhas, lápis, borracha.