Aquecimento
Plano de Aula
Plano de aula: Aproximação inicial do conceito de área
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Medidas de Superfície
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Letícia de Queiroz Maffei
Mentor: Marcella de Oliveira Abreu Fontinele
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF03MA21) Comparar, visualmente ou por superposição, áreas de faces de objetos, de figuras planas ou de desenhos.
Objetivos específicos
Determinar áreas de diferentes superfícies, utilizando contagem ou superposição de figuras.
Conceito-chave
Área de figuras planas.
Recursos necessários
- Tesoura;
- Lápis de cor;
- Atividades impressas em folhas.
Habilidades BNCC:
Objetivos de aprendizagem
Determinar áreas de diferentes superfícies, utilizando contagem ou superposição de figuras.
Resumo da aula
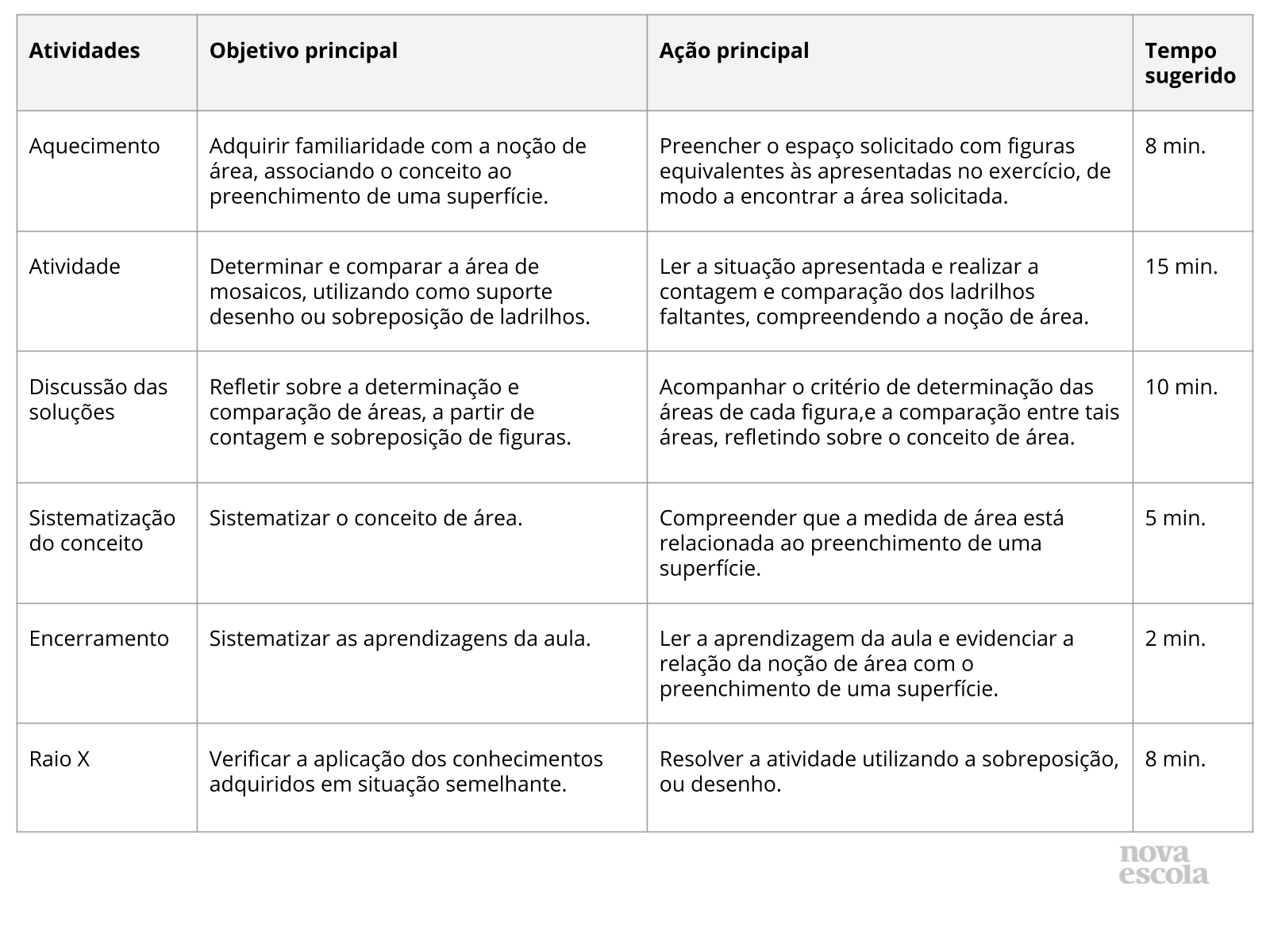
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 10 minutos (slides 3 e 4).
Orientações: Entregue a folha de atividade e os quadradinhos desenhados por Carol. O material foi produzido em uma escala de tamanhos equivalentes, e em um tamanho que seja acessível ao manuseio dos alunos. Os alunos deverão recortar os quadradinhos e utilizar como referência para a contagem através da sobreposição. A área está relacionada com a cobertura de superfícies, neste caso, os alunos deverão calcular a quantidade necessária de quadradinhos para completar o painel de Carolina. Serão utilizados os quadradinhos modelo sobrepostos na figura, de modo que eles possam verificar se a quantidade de quadradinhos desenhado por Carol será suficiente para completar o painel. O intuito é fazer com que eles percebam que o cálculo da área está vinculado ao preenchimento de determinada superfície com uma medida referencial que, nesta atividade, são os quadradinhos.
Propósito: Fazer com que os alunos determinem a área através da cobertura (superposição) ou preenchimento de determinada superfície.
Discuta com a turma:
- Vocês conseguem ajudar Carol? Se precisarem recortem os quadradinhos que ela desenhou e ajudem a conferir se são suficientes!
- Será que se os quadradinhos ainda não estivessem desenhados e prontos para recortarmos, teríamos outro jeito de saber quantos seriam necessários? (desdobramento desta pergunta no próximo slide)
Materiais complementares para impressão:
Aquecimento

Tempo sugerido: 10 minutos (slides 3 e 4).
Orientações: Questione os alunos sobre as possibilidades para descobrir o total de quadradinhos necessários para o preenchimento do mural. Inicialmente, eles receberam a atividade e uma malha equivalente aos quadradinhos que Carol desenhou, mas se esses quadradinhos ainda não estivessem desenhados, eles teriam outra forma de chegar à quantidade necessária? Instigue-os a apresentarem possibilidades para descobrir o total de quadradinhos para cobrir a parte incompleta do mural.
Discuta com a turma:
- Como vocês fariam se não tivéssemos os quadradinhos que Carol desenhou?
- De que outra forma podemos descobrir quantos quadradinhos serão necessários para completar o mural novamente?
- Se fôssemos tentar desenhar esses espaços que os quadradinhos ocupariam, seria possível? Como poderia ser feito?
Atividade principal
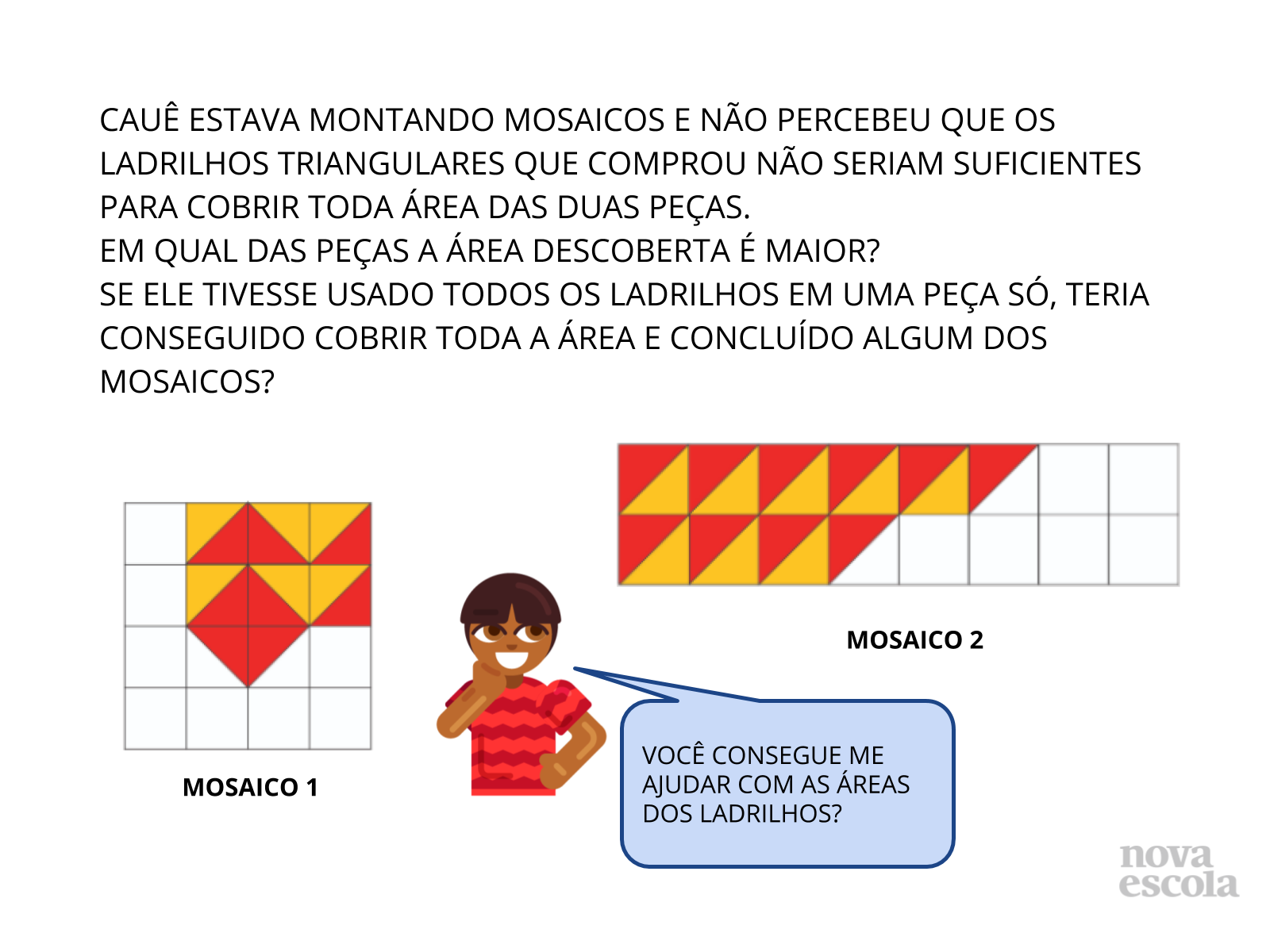
Tempo sugerido: 15 minutos.
Orientações: Distribua a atividade impressa aos alunos. Oriente que, primeiramente, descubram quantos ladrilhos seriam necessários para preencher cada mosaico. Sugira a eles utilizarem os ladrinhos de malhas (entregue junto com a atividade), ou que recortem uma das peças para usarem como quebra-cabeças sobre a outra, mas cuidado para não tirar pedaços das peças (eles precisam conseguir montar novamente, se precisarem). Para a segunda etapa, eles precisarão calcular o que cada peça já possui e o quanto falta e, assim, conseguirem ver se daria para fazer um mosaico completo se usassem todas as peças em apenas um deles.
Discuta com a turma:
- Cauê fez dois mosaicos. Quer dizer, tentou fazer, mas faltaram peças! Vocês conseguem ajudar Cauê a descobrir quantos ladrilhos ficaram faltando em cada uma?
- Para ajudar na contagem vocês podem utilizar os ladrilhos que receberam na malha entregue juntamente com a atividade, ou podem recortar cuidadosamente uma das peças e tentar montar como um quebra cabeça sobre a outra. Mas cuidado! Cauê precisa de tudo inteiro depois! Qual será o jeito mais prático?
- Agora que sabemos quantas faltam em cada, será que se ele tivesse usado tudo em uma peça só, teria conseguido deixar pelo menos um mosaico pronto? É um mosaico e podemos ser bem criativos, não se preocupem com as cores, e sim, com os espaços que precisamos preencher!
- O que vocês podem dizer sobre a área de cada mosaico? Eles são diferentes, suas áreas também?
Materiais complementares para impressão:
Resolução da atividade principal
Discussão de soluções

Tempo sugerido: 10 minutos (Slides 6 a 13).
Orientações: Depois que os alunos compartilharem as estratégias deles, mostrando seus desenhos e explicando oralmente, passe para esta série de slides. Nela, os alunos verão passo a passo algumas das possibilidades para ajudar Cauê a analisar seus mosaicos. Tente evidenciar aquelas soluções que já foram apresentadas por eles e acrescente como possibilidade aquelas que talvez não tenham aparecido nas resoluções apresentadas pela turma. Destaque que, neste caso, Cauê já ajudou fazendo as marquinhas quadriculadas em seus mosaicos (mesmo na parte em que ainda não havia colado ladrilhos), mas que sempre cuidaremos para preencher as áreas que queremos medir com as figuras uma exatamente ao lado da outra, e usando nossa unidade de referência (no caso o triângulo, que é o formato do ladrilho).
Propósito: Realizar um fechamento das ideias exploradas até o momento.
Discuta com a turma:
- Para ajudar a contar, vocês poderiam desenhar os ladrilhos, ou recortar na malha de papel que receberam e colocar sobre cada um dos mosaicos. Conseguiram chegar a um total de ladrilhos?
- Quantos ladrilhos faltam na primeira figura? Quantos faltam na segunda? Em qual falta mais?
- Como vocês fizeram para não se perder na hora de contar o total de ladrilhos que faltavam? (Alguns fazem pequenas marquinhas na figura, outros podem seguir a contagem por linhas e colunas)
Discussão de soluções
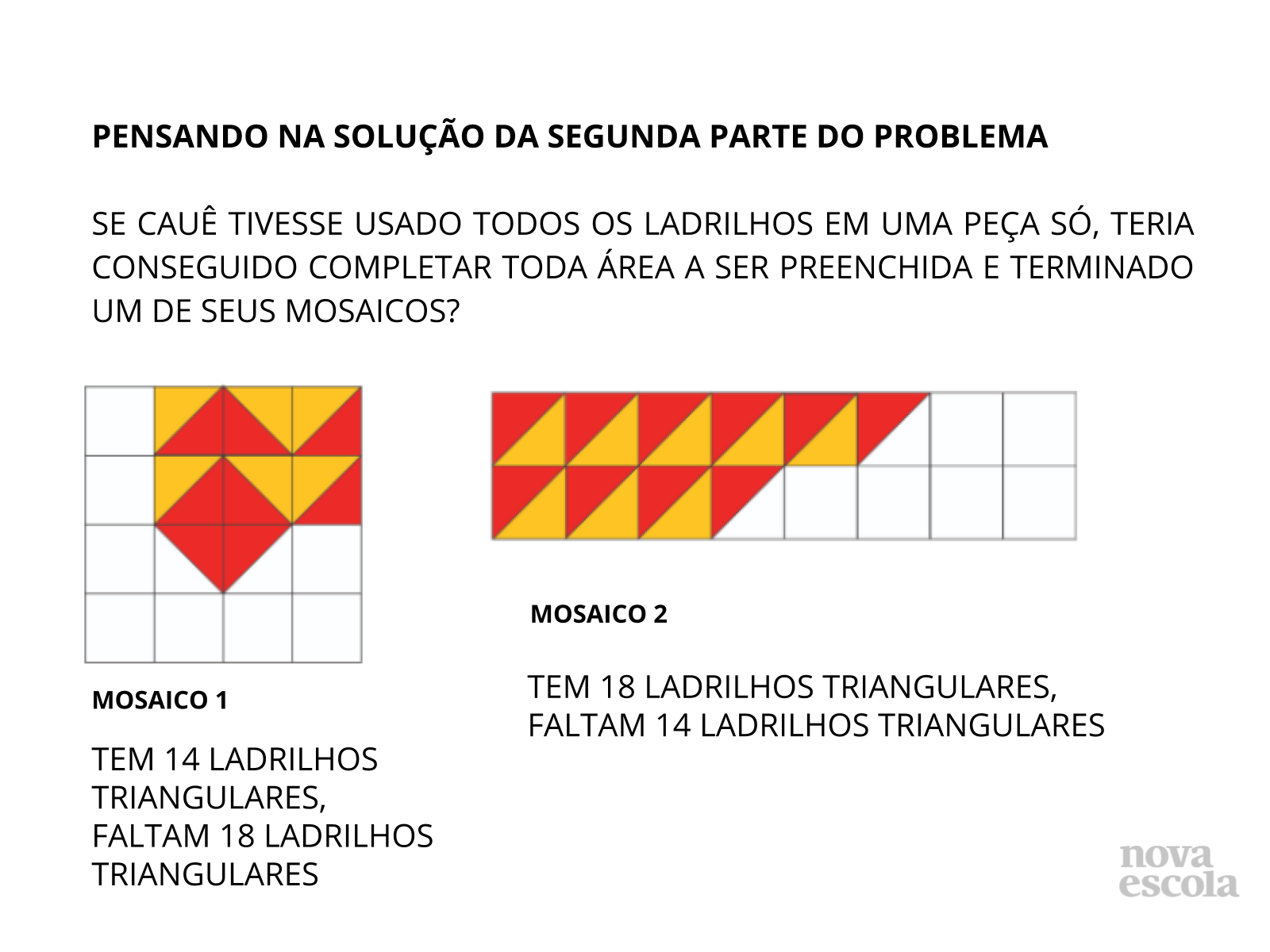
Tempo sugerido: 10 minutos (Slides 6 a 13).
Orientações: Apresente a segunda parte da resolução, na qual eles precisam analisar se é possível preencher um mosaico, caso utilizem as peças do outro para completá-lo. Esta primeira solução está apresentada com base na contagem dos ladrilhos, considerando que já foram contabilizados os totais de ladrilhos faltantes em cada um dos mosaicos, portanto, bastaria que os alunos contassem o total de ladrilhos já colocados e fizessem as comparações.
Propósito: Realizar um fechamento das ideias exploradas até o momento.
Discuta com a turma:
- O que precisamos fazer para saber se o número de ladrilhos seria suficiente para preencher um mosaico inteiro?
- Será que os valores que encontramos na primeira etapa da atividade nos ajudam a chegar ao resultado?
- Quantos ladrilhos já estão colocados em cada peça? Quantos faltam?
- Se não quisermos contar quantos ladrilhos faltam em cada peça podemos usar alguma outra estratégia? (ver slides 8 e 9)
- Qual mosaico ele conseguiria completar? O Mosaico 1? O Mosaico 2?
- Por que vocês acham que chegamos a essa resposta? (Conseguir completar tanto um quanto o outro).
- Qual a área total de cada mosaico? (ver slides 10 e 11)
Discussão de soluções
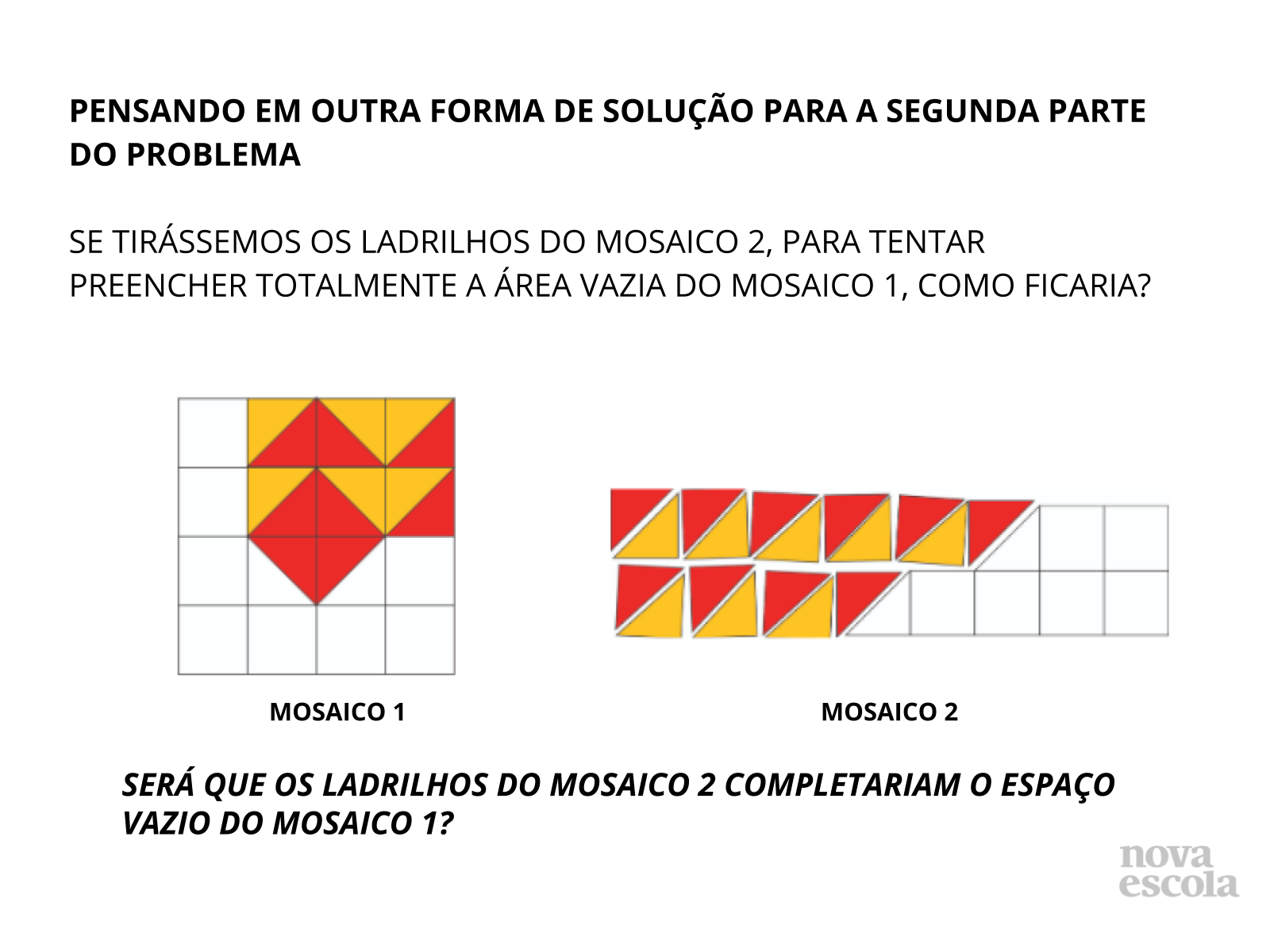
Tempo sugerido: 10 minutos (Slides 6 a 13).
Orientações: Explore a possibilidade de utilizar os ladrilhos de um mosaico para tentar completar o outro. Faça os alunos pensarem como se pudéssemos destacar as peças que foram usadas em um dos mosaicos na tentativa de completar o espaço vazio do outro. Os alunos podem utilizar a malha para recortar como forma de representar os ladrilhos considerados.
Propósito: Realizar um fechamento das ideias exploradas até o momento.
Discuta com a turma:
- O que poderíamos fazer para saber se o número de ladrilhos seria suficiente para preencher um mosaico inteiro se não quiséssemos contar ladrilho por ladrilho? (sobrepor as peças)
- Poderíamos fazer o aproveitamento dos ladrilhos de um mosaico no outro e ver se seriam suficientes?
- Tirando todos os ladrilhos utilizados no Mosaico 2, e colocando sobre os espaços vazios do Mosaico 1, conseguimos terminar o Mosaico 1?
Discussão de soluções
Tempo sugerido: 10 minutos (Slides 6 a 13).
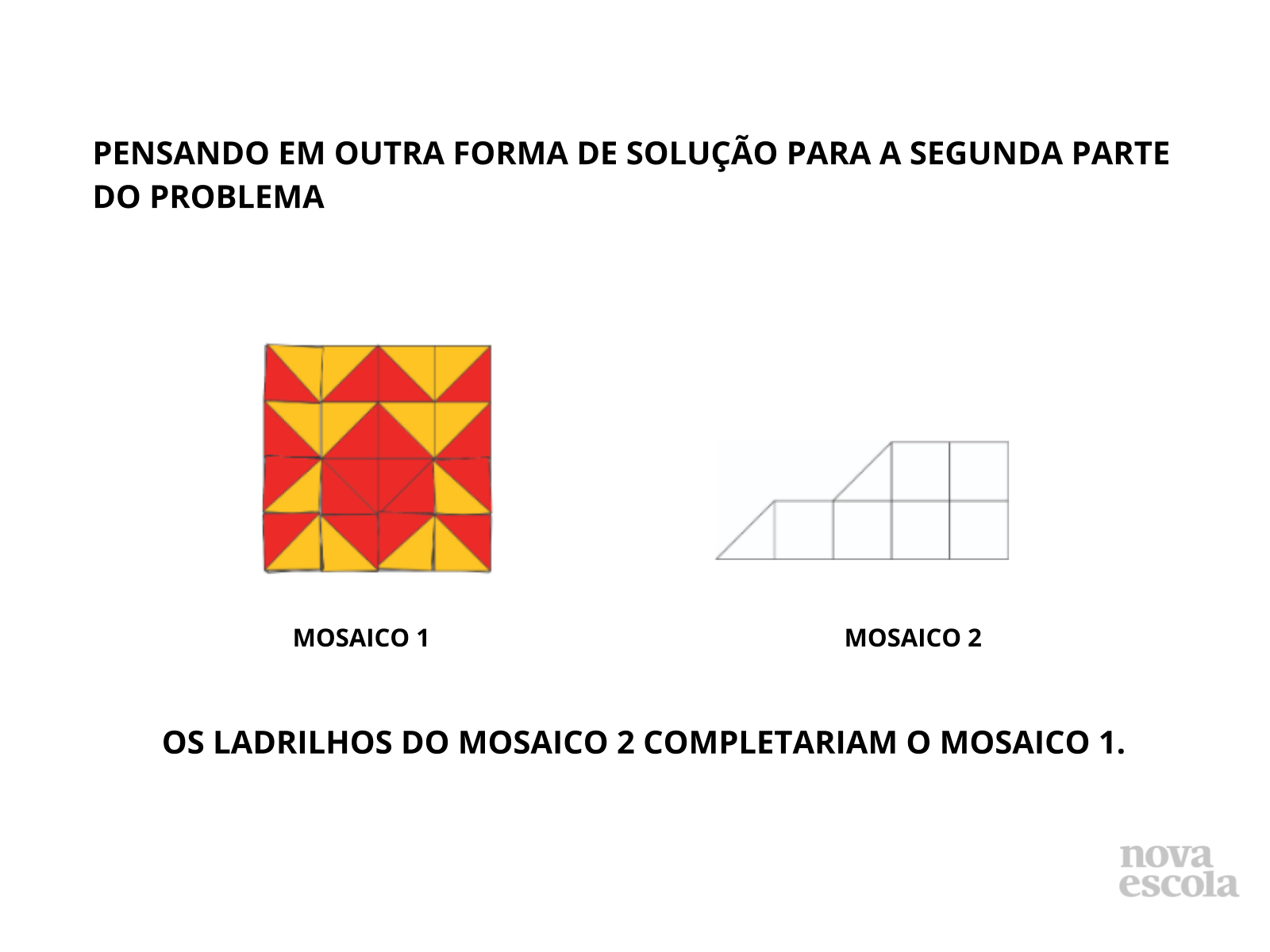
Orientações: Apresente uma das soluções de construção utilizando os ladrilhos do mosaico 2 para preencher o mosaico 1. Os alunos deverão perceber que as peças utilizadas para a construção do segundo são suficientes para preencher o primeiro. Questione-os sobre a possibilidade contrária (com os ladrilhos do mosaico 1 conseguir preencher o vazio do mosaico 2).
Propósito: Realizar um fechamento das ideias exploradas até o momento.
Discuta com a turma:
- O que podemos perceber observando a figura?
- Tirando todos os ladrilhos utilizados no Mosaico 2, e colocando sobre os espaços vazios do Mosaico 1, conseguimos terminar o Mosaico 1?
- E o contrário? Seria possível? Preencher o espaço vazio do Mosaico 2 com os ladrilhos do Mosaico 1?
Discussão de soluções
Tempo sugerido: 10 minutos (Slides 6 a 13).
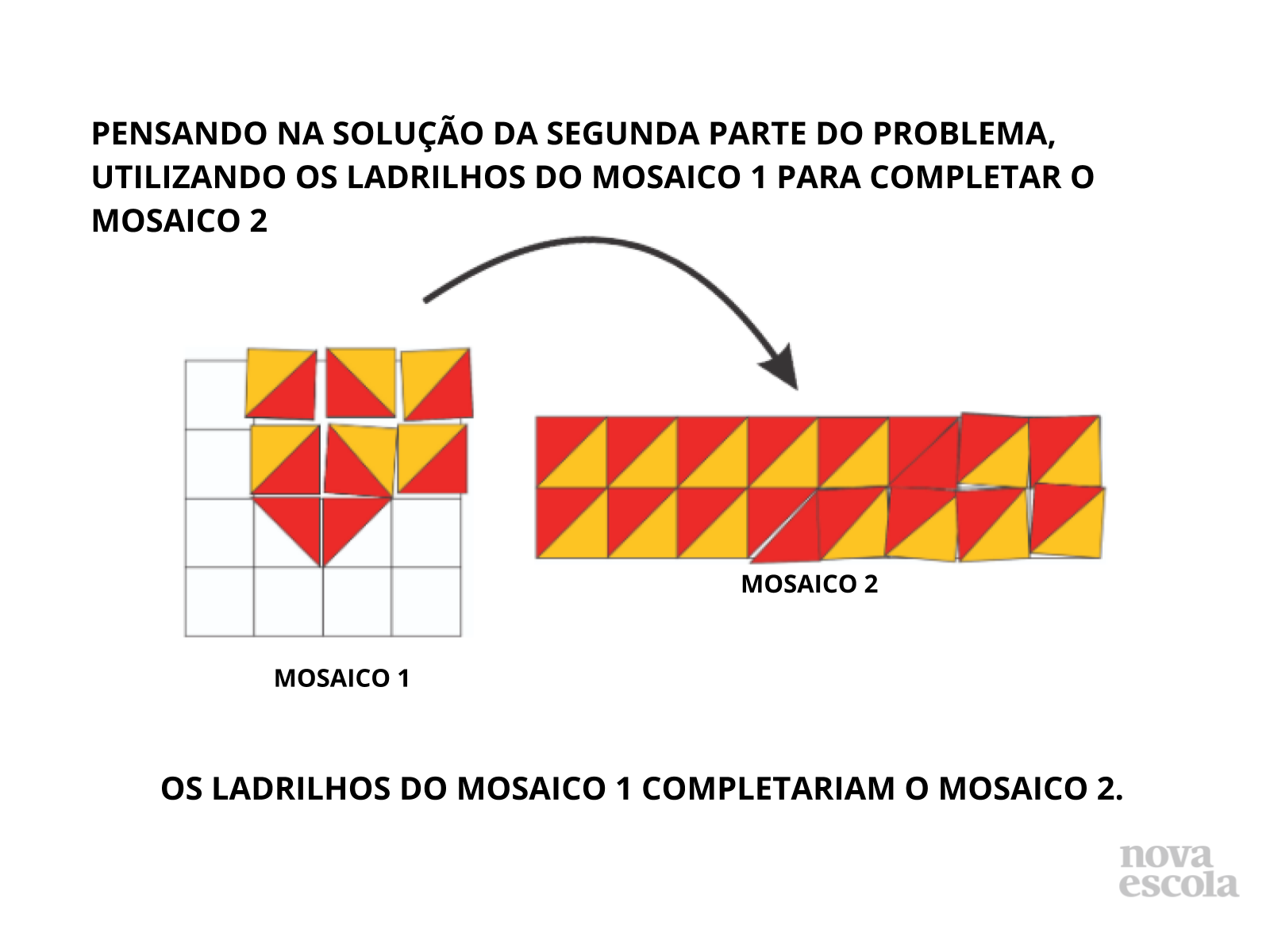
Orientações: Apresente uma das possibilidades de soluções utilizando os ladrilhos do mosaico 1 para preencher o mosaico 2. Os alunos deverão perceber que as peças utilizadas para a construção do primeiro são suficientes para preencher o segundo. Os alunos perceberão que é possível preencher o mosaico 2 com as peças do mosaico 1. Por que será que foi possível preencher tanto um quanto o outro mosaico? Questionar se tem algum motivo para que os dois mosaicos pudessem ser preenchidos.
Propósito: Realizar um fechamento das ideias exploradas até o momento.
Discuta com a turma:
- O que podemos perceber observando a figura?
- Tirando todos os ladrilhos utilizados no Mosaico 1 e colocando sobre os espaços vazios do Mosaico 2 conseguimos terminar o Mosaico 2?
- O que podemos perceber em relação aos dois mosaicos?
Discussão de soluções

Tempo sugerido: 10 minutos (Slides 6 a 13).
Orientações: Apresente os dois mosaicos completos e instigue os alunos a dizerem o que ambos têm em comum. Além do fato de serem preenchidos pelo mesmo tipo de ladrilho triangular, eles deverão perceber que ambos necessitam da mesma quantidade de ladrilhos para serem preenchidos. Dizer que as duas superfícies necessitam da mesma quantidade de ladrilhos para ser preenchida, é dizer que ambas têm a mesma área.
Propósito: Realizar um fechamento das ideias exploradas até o momento.
Discuta com a turma:
- O que podemos perceber observando as figuras?
- Além de serem formadas por ladrilhos triangulares o que mais os dois ladrilhos possuem em comum?
- Quantos ladrilhos foram necessários para preencher o mosaico 1? E o mosaico 2?
- Se ambos mosaicos precisam da mesma quantidade de ladrilhos para serem preenchidos, o que eles têm em comum? [a medida da superfície, a área]
Discussão de soluções
Tempo sugerido: 10 minutos (Slides 6 a 13).
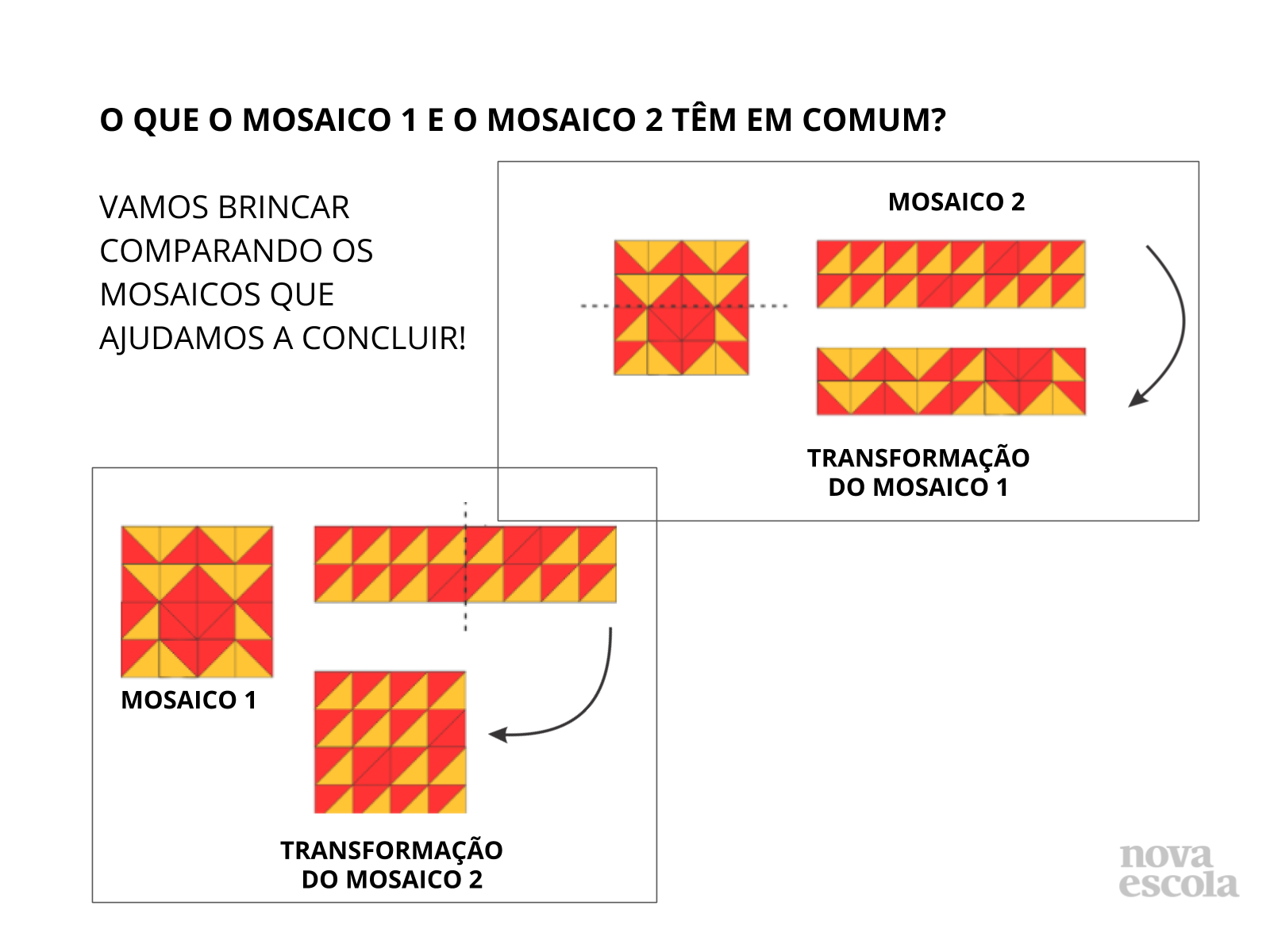
Orientações: Mostre como seria se partíssemos um dos dois mosaicos ao meio. Ao partir os mosaicos ao meio, poderíamos transformá-los no mesmo formato do outro mosaico. Ao apresentar tal perspectiva de desconstrução e transformação de uma peça em outra, podemos complementar a história em torno dos mosaicos de Cauê.
Propósito: Realizar um fechamento das ideias exploradas até o momento.
Discuta com a turma:
- O que podemos perceber observando as figuras?
- Olhando rapidamente vocês diriam que os dois mosaicos têm a mesma área? E agora que observamos o total de ladrilhos necessários, qual mosaico vocês acham que Cauê deveria tentar concluir?
Discussão de soluções

Tempo sugerido: 10 minutos (Slides 6 a 13).
Orientações: Complete a história em torno dos mosaicos de Cauê.
Propósito: Realizar um fechamento das ideias exploradas até o momento.
Discuta com a turma:
- O que podemos perceber observando as figuras?
- Olhando rapidamente vocês diriam que os dois mosaicos têm a mesma área? E agora que observamos o total de ladrilhos necessários, qual mosaico vocês acham que Cauê deveria tentar concluir?
Sistematização do conceito

Tempo sugerido: 5 minutos.
Orientações: Sistematize o conceito trabalhado, retomando com os estudantes a relação do preenchimento da superfície com a área a ser representada. Destaque a necessidade de determinarmos uma unidade como referência (podem ser os quadradinhos, ou os triângulos, futuramente serão mais comumente usados metros ou centímetros quadrados) para preencher a área a ser determinada e ao realizar este preenchimento cuidar para que as unidades de referência sejam dispostas exatamente lado a lado, com o mínimo de espaços e sobreposições entre elas.
Propósito: Sistematizar o conceito aprendido em aula.
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes a relação do preenchimento da superfície com a área representada. Apresente as figuras exploradas nas atividades anteriores e retome como podem ser identificadas as áreas de espaços desconhecidos (aqueles que queríamos preencher nas atividades) ou até mesmo a área total de uma figura.
Propósito: Retomar a atividade da aula.
Raio x

Tempo sugerido: 7 minutos
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem utilizando como referência o recorte da malha de ladrilhos, entregue junto com a atividade, ou a própria parede de ladrilhos disponibilizada no desenho. A atividade não deverá ser respondida com apenas sim ou não, mas o aluno deve explicar para Roberta se poderia, ou não, aproveitar os azulejos, dizendo qual a possibilidade ou o porquê de não ser possível. Incentive que os alunos apresentem uma solução detalhada para Roberta, como se fossem o pedreiro que está fazendo a obra e precisa justificar a ela o que poderia fazer, se poderia ou se não poderia. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando a solução no quadro.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante, e avaliar os conhecimentos de cada um a respeito do preenchimento da malha quadriculada como forma de chegar à medida de área desejada.
Materiais complementares para impressão:
Resolução da atividade complementar
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Letícia de Queiroz Maffei
Mentor: Marcella de Oliveira Abreu Fontinele
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF03MA21) Comparar, visualmente ou por superposição, áreas de faces de objetos, de figuras planas ou de desenhos.
Objetivos específicos
Determinar áreas de diferentes superfícies, utilizando contagem ou superposição de figuras.
Conceito-chave
Área de figuras planas.
Recursos necessários
- Tesoura;
- Lápis de cor;
- Atividades impressas em folhas.











