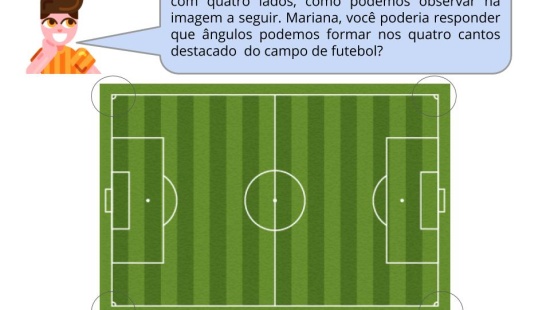
Resumo da aula
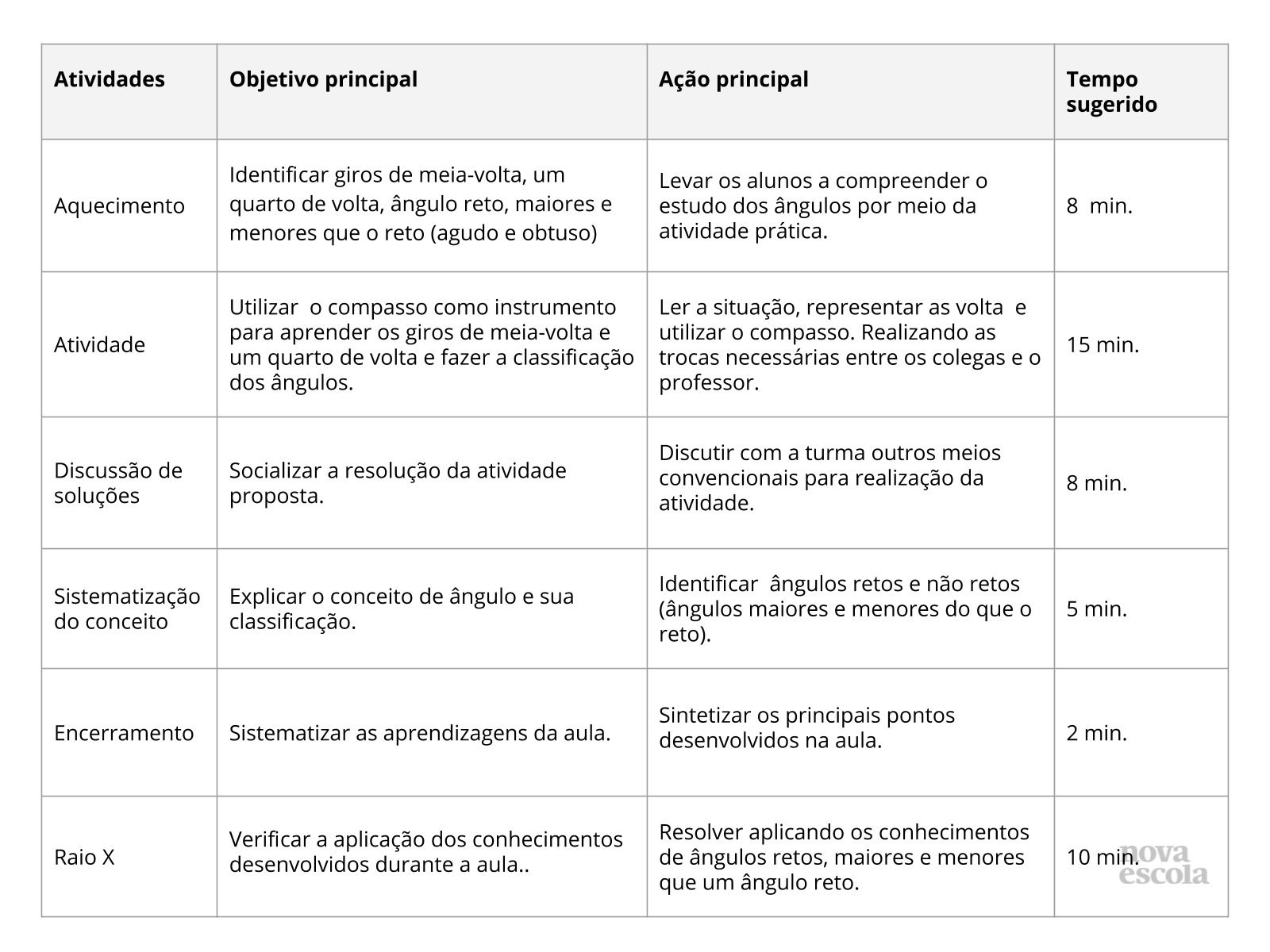
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 8 minutos.
Orientações: Essa atividade é bem simples, mas requer bastante atenção dos alunos no momento da explicação. Como é uma atividade prática, os alunos precisam colaborar com o comportamento. Converse antes com eles e dê as orientações necessárias. Professor você deverá ficar atento ao andamento da aula e observar o aproveitamento dos alunos, sanando as possíveis dúvidas que aparecerem durante a aulas.
Inicialmente os alunos deverão ficar em pé de forma ereta e com as mãos na cintura. Em seguida deverão virar o corpo para o lado direito, representando ¼ de volta. Caso surja dúvida explique o que é ¼ de volta. Depois peça para o aluno continuar girando para o mesmo lado e completar outro ¼ de volta (ele ficará com o corpo para trás). Em seguida peça ao aluno girar novamente dando o terceiro ¼ de volta (ele ficará na posição lateral). Por último solicite que complete o último ¼ de volta finalizando a volta inteira. Comente com o aluno que o ângulo de uma volta inteira mede 360º.
Propósito: Compreender que é possível entender o estudo dos ângulos utilizando apenas o corpo como instrumento.
Discuta com a turma:
- Quantos giros foram necessários para dar uma volta completa? Por quê chamamos cada giro de ¼ de volta?
- Se o ângulo de uma volta inteira mede 360º quanto representaria cada giro de ¼ de volta?
- Quando você girou 2 vezes qual seria a medida do ângulo que você girou ao todo? E quanto você girou 3 vezes?
- Qual seria a medida do ângulo de meia-volta?
Atividade Principal (Slides 4 e 5)

Tempo sugerido: 15 minutos.
Orientações: Iremos utilizar nesta atividade o compasso para facilitar a construção da circunferência e compreensão do aluno quanto a atividade proposta sobre ângulos. Distribua aos alunos folhas brancas para realizarem a atividade proposta. Quando os alunos cortarem o círculo ao meio formará duas metades cujo ângulo central de cada uma mede 180°. Ao cortarem o pedaço cuja medida é 180º ao meio formarão outras duas metades cada uma com medida de 90°. Logo cada pedaço obtido cabe 4 vezes no círculo original e possui ângulo central medindo 90º cada um.
Em seguida peça aos alunos procurarem objetos na sala de aula que apresentem ângulos cujas medidas sejam exatamente, menor que ou maior que 90º. Os alunos terão liberdade de andar pela sala e supervisão sua e poderão encontrar respostas variadas como, por exemplo, o canto da lousa, da porta, a abertura do pé da cadeira, os ângulos formados entre as paredes, etc.
Propósito: Usar o ângulo de ¼ de volta para comparar os ângulos ao seu redor e classificá-los.
Discuta com a turma:
- Quando você recortou o círculo o quê você reparou nos lados que obteve? A abertura deles foi ficando maior ou menor?
- Caso você quisesse continuar recortando o círculo o que acha que aconteceria?
- E se você fosse juntando vários pedaços diferentes do círculo? Que tipos de ângulo você acha que conseguiria formar?
- Quais objetos fora da sala de aula você acredita que apresentem ângulos retos, agudos ou obtusos?
- Você saberia dizer outras situações do dia-a-dia que envolvem giros e ângulos?
Materiais para Impressão:
Atividade principal
Resolução da atividade
Guia de intervenção
Para saber mais acesse: http://portaldoprofessor.mec.gov.br/storage/materiais/0000012800.pdf
Atividade Principal (Slides 4 e 5)

Tempo sugerido: 15 minutos.
Orientações: Iremos utilizar nesta atividade o compasso para facilitar a construção da circunferência e compreensão do aluno quanto a atividade proposta sobre ângulos. Distribua aos alunos folhas brancas para realizarem a atividade proposta. Quando os alunos cortarem o círculo ao meio formará duas metades cujo ângulo central de cada uma mede 180°. Ao cortarem o pedaço cuja medida é 180º ao meio formarão outras duas metades cada uma com medida de 90°. Logo cada pedaço obtido cabe 4 vezes no círculo original e possui ângulo central medindo 90º cada um.
Em seguida peça aos alunos procurarem objetos na sala de aula que apresentem ângulos cujas medidas sejam exatamente, menor que ou maior que 90º. Os alunos terão liberdade de andar pela sala e supervisão sua e poderão encontrar respostas variadas como, por exemplo, o canto da lousa, da porta, a abertura do pé da cadeira, os ângulos formados entre as paredes, etc.
Propósito: Usar o ângulo de ¼ de volta para comparar os ângulos ao seu redor e classificá-los.
Discuta com a turma:
- Quando você recortou o círculo o quê você reparou nos lados que obteve? A abertura deles foi ficando maior ou menor?
- Caso você quisesse continuar recortando o círculo o que acha que aconteceria?
- E se você fosse juntando vários pedaços diferentes do círculo? Que tipos de ângulo você acha que conseguiria formar?
- Quais objetos fora da sala de aula você acredita que apresentem ângulos retos, agudos ou obtusos?
- Você saberia dizer outras situações do dia-a-dia que envolvem giros e ângulos?
Para saber mais acesse: http://portaldoprofessor.mec.gov.br/storage/materiais/0000012800.pdf
Discussão da solução
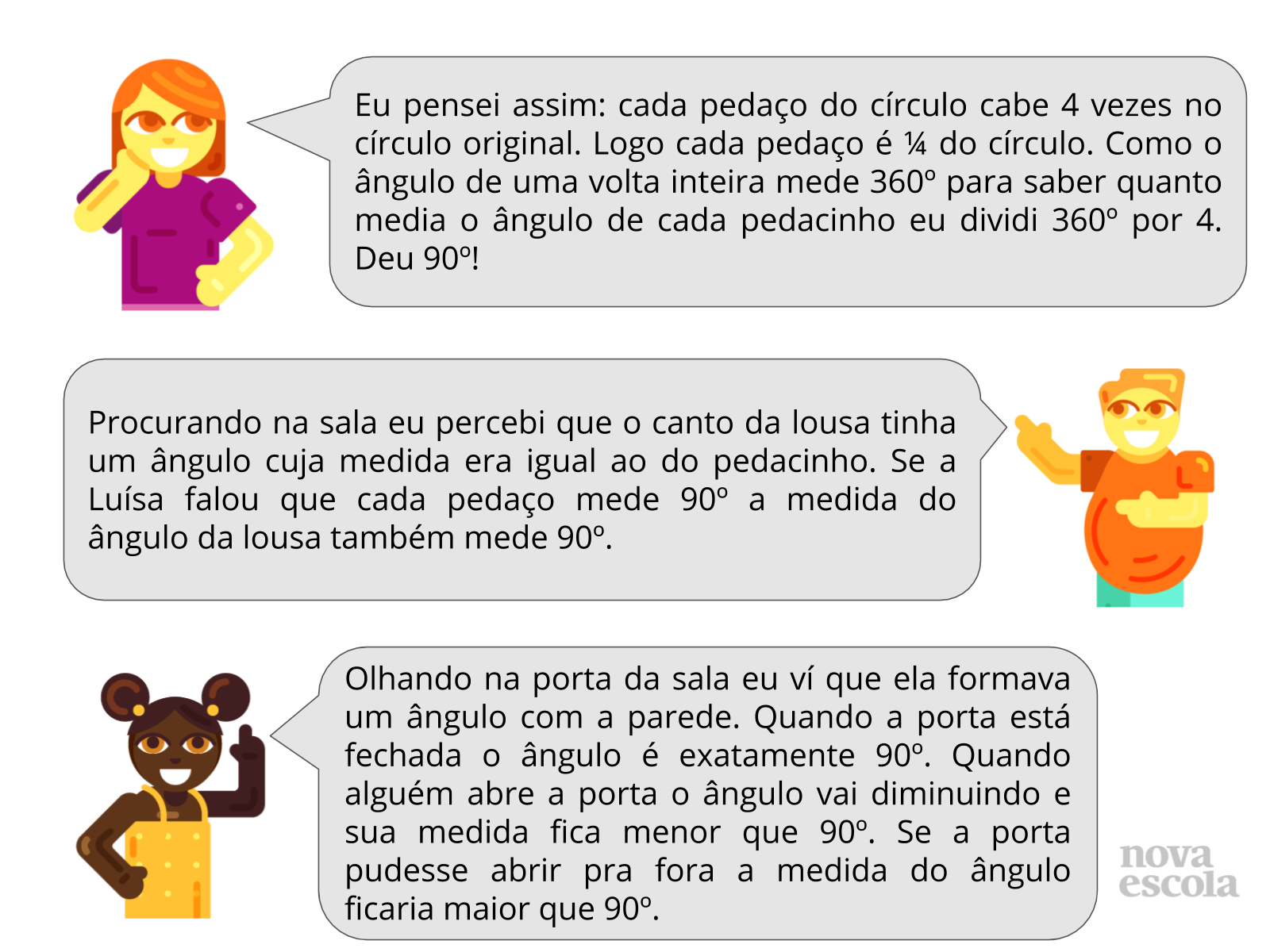
Tempo sugerido: 8 minutos.
Orientações: Neste momento compare os resultados obtidos pelos alunos procurando separá-los entre os mais recorrentes que a turma apresentou e aqueles usaram ideias mais diferentes. Quando houver necessidade intervenha aproximando a linguagem do aluno à linguagem usada em Matemática. Fique atento à definição de ângulo como região plana delimitada por duas semirretas de mesma origem. Outro fator importante é associar a medida do ângulo com a abertura formada por estas duas semirretas: quanto maior for a abertura maior será a medida do ângulo.
Propósito: Socializar as descobertas das medidas dos ângulos de elementos da sala de aula.
Sistematização do conceito

Tempo sugerido: 5 minutos.
Orientações: Projete o slide ou escreva na lousa os principais momentos da aula associando aos conceitos matemáticos envolvidos. Você irá refinar os conceitos desenvolvidos ao longo da aula dando o enfoque matemático necessário. Fique atento à diferenciar ângulos que representam giros e ângulos que representam regiões do plano delimitadas por duas semirretas de mesma origem. Outro fator importante é que ao realizarmos medições estamos envolvendo a comparação entre grandezas. No momento não há necessidade de definirmos uma unidade de medida padrão (1º é um 360 avos da circunferência). Apenas classifique os ângulos tendo como referência a medida do ângulo reto.
Propósito: Classificar os ângulos em retos, agudos e obtusos.
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Neste momento faremos o fechamento da aula elencando os principais resultados obtidos durante a aula. Sempre que o aluno sentir necessidade ele poderá usar esta informação. No caso as informações pertinentes desta aula são as medidas obtidas com os giros e os tipos de ângulos.
Propósito: Retomar os principais pontos desenvolvidos na aula.
Raio X
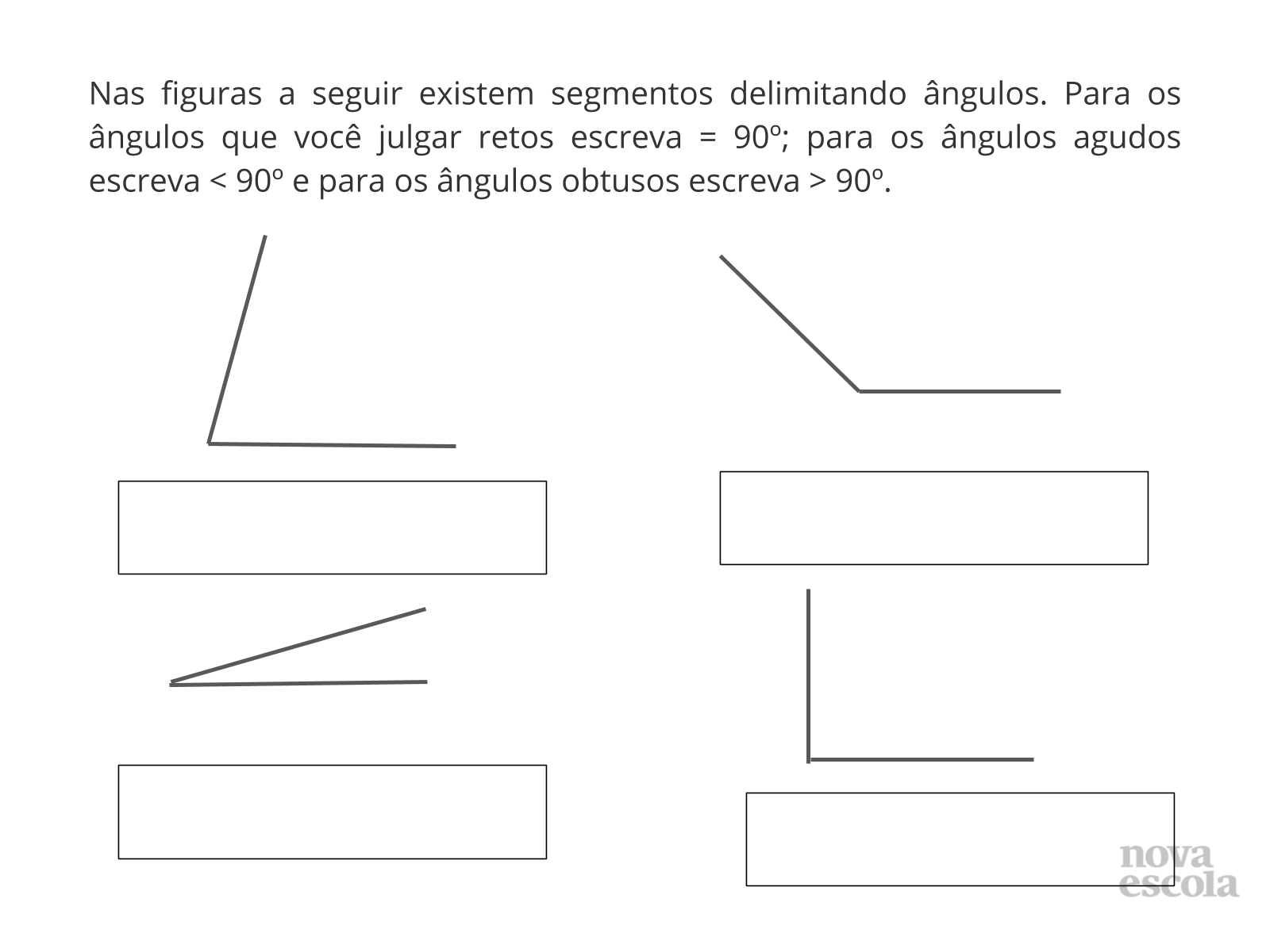
Tempo sugerido: 10 minutos.
Orientações: Entregue uma folha impressa para cada aluno com os ângulos sugeridos e peça para eles classificarem os ângulos de acordo com a abertura dos segmentos. Não há necessidade de uso do transferidor. Peça apenas que o aluno analise a abertura formada pelos lados dos ângulos.
Propósito: Verificar se o objetivo da aula foi atingido (associar os giros às representações dos ângulos).
Discuta com a turma:
- Qual seria a definição formal de ângulo reto? E de ângulo agudo? E do ângulo obtuso?
- Existem outros tipos de ângulos que poderíamos usar na classificação?
- O que seria um ângulo nulo? E um ângulo de meia-volta?
Materiais para impressão:
Raio X para impressão
Resolução do Raio X
Atividade complementar
Resolução da Atividade complementar