Malha Quadriculada
Plano de Aula
Plano de aula: Perímetro e Área de figuras e plantas irregulares
Plano 4 de uma sequência de 5 planos. Veja todos os planos sobre Plantas baixas: explorando área e perímetro
Por: Elizabeth Bento
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Elizabeth Bento
Mentora: Maria Aparecida Nemet
Revisor: Rodrigo Morozetti Blanco
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA26) Interpretar, descrever e desenhar plantas baixas simples de residências e vistas aéreas.
Habilidades necessárias
Trabalhar com malhas retangulares e triangulares, decompor um polígono em regiões mais simples (quadrado, retângulo e triângulo)
Objetivos específicos
Determinar áreas e perímetros de plantas irregulares.
Conceito-chave
Planta baixa, perímetro, área.
Recursos necessários
-Malha retangular;
-Sulfite;
-Lápis de cor;
-Régua.
Habilidades BNCC:
Objetivos de aprendizagem
Determinar áreas e perímetros de plantas irregulares.
Resumo da Aula
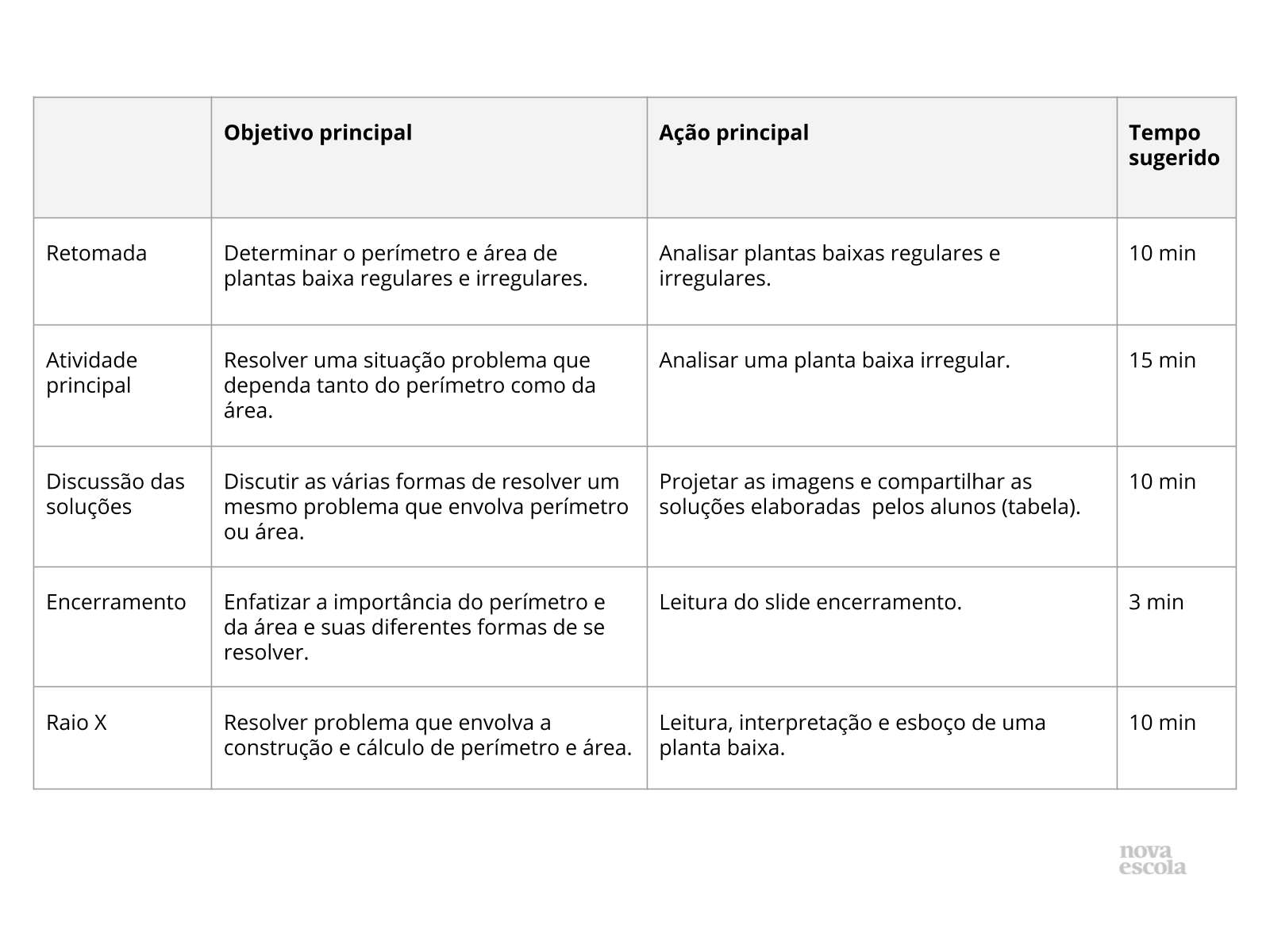 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Leia o objetivo com a turma e pergunte quais os conhecimentos prévios deles acerca desse assunto.
Propósito: Compartilhar com a turma o objetivo da aula
Retomada (Slides 3 e 4)

Tempo sugerido: 10 minutos.
Orientação: Para esta atividade é necessário distribuir a malha quadriculada 0,5 x 1 e realizar a leitura do slide 3. Antes de seguir para o slide 4, peça que eles digam o que é possível fazer com as informações do enunciado.
Organize então a sala em trios e apresente o slide 4, pedindo que eles determinem quais são as tarefas a serem solucionadas por cada um:
- desenhar a planta inteira da praça;
- determinar a quantidade de cerca necessária para área verde;
- determinar as medidas de áreas dos espaços nas cores cinza e verde.
Você pode também apresentar a atividade impressa, caso não seja possível projetá-la. Caso os alunos apresentem dificuldade em utilizar malhas com escalas diferentes consulte o guia de intervenções.
Esse tipo de aula onde são apresentados diferentes desafios (nessa aula serão apresentados 3 desafios, além das atividades complementares) pode ser explorado com os princípios de gameficação, onde os alunos ganham pontos a cada desafio resolvido individualmente ou em grupo como se estivessem “passando de fase” em um game.
Propósito: Ler a planta identificando suas medidas de perímetro e área.
Discuta com a turma:
- Para ser a metade da área e do perímetro é necessário ter o mesmo formato? (verifique painel de soluções)
- Faz diferença saber que a parte a ser desenhada é simétrica?(verifique painel de soluções)
- Você poderia identificar outras simetrias existentes ao seu redor?
- Quando há simetria entre duas figuras o perímetro e área serão sempre os mesmo?
Materiais complementares:
Retomada (Slides 3 e 4)

Tempo sugerido: 10 minutos.
Orientação: Para esta atividade é necessário distribuir a malha quadriculada 0,5 x 1 e realizar a leitura do slide 3. Antes de seguir para o slide 4, peça que eles digam o que é possível fazer com as informações do enunciado.
Organize então a sala em trios e apresente o slide 4, pedindo que eles determinem quais são as tarefas a serem solucionadas por cada um:
- desenhar a planta inteira da praça;
- determinar a quantidade de cerca necessária para área verde;
- determinar as medidas de áreas dos espaços nas cores cinza e verde.
Você pode também apresentar a atividade impressa, caso não seja possível projetá-la. Caso os alunos apresentem dificuldade em utilizar malhas com escalas diferentes consulte o guia de intervenções.
Esse tipo de aula onde são apresentados diferentes desafios (nessa aula serão apresentados 3 desafios, além das atividades complementares) pode ser explorado com os princípios de gameficação, onde os alunos ganham pontos a cada desafio resolvido individualmente ou em grupo como se estivessem “passando de fase” em um game.
Propósito: Ler a planta identificando suas medidas de perímetro e área.
Discuta com a turma:
- Para ser a metade da área e do perímetro é necessário ter o mesmo formato? (verifique painel de soluções)
- Faz diferença saber que a parte a ser desenhada é simétrica?(verifique painel de soluções)
- Você poderia identificar outras simetrias existentes ao seu redor?
- Quando há simetria entre duas figuras o perímetro e área serão sempre os mesmo?
Atividade principal (Slides 5 e 6)
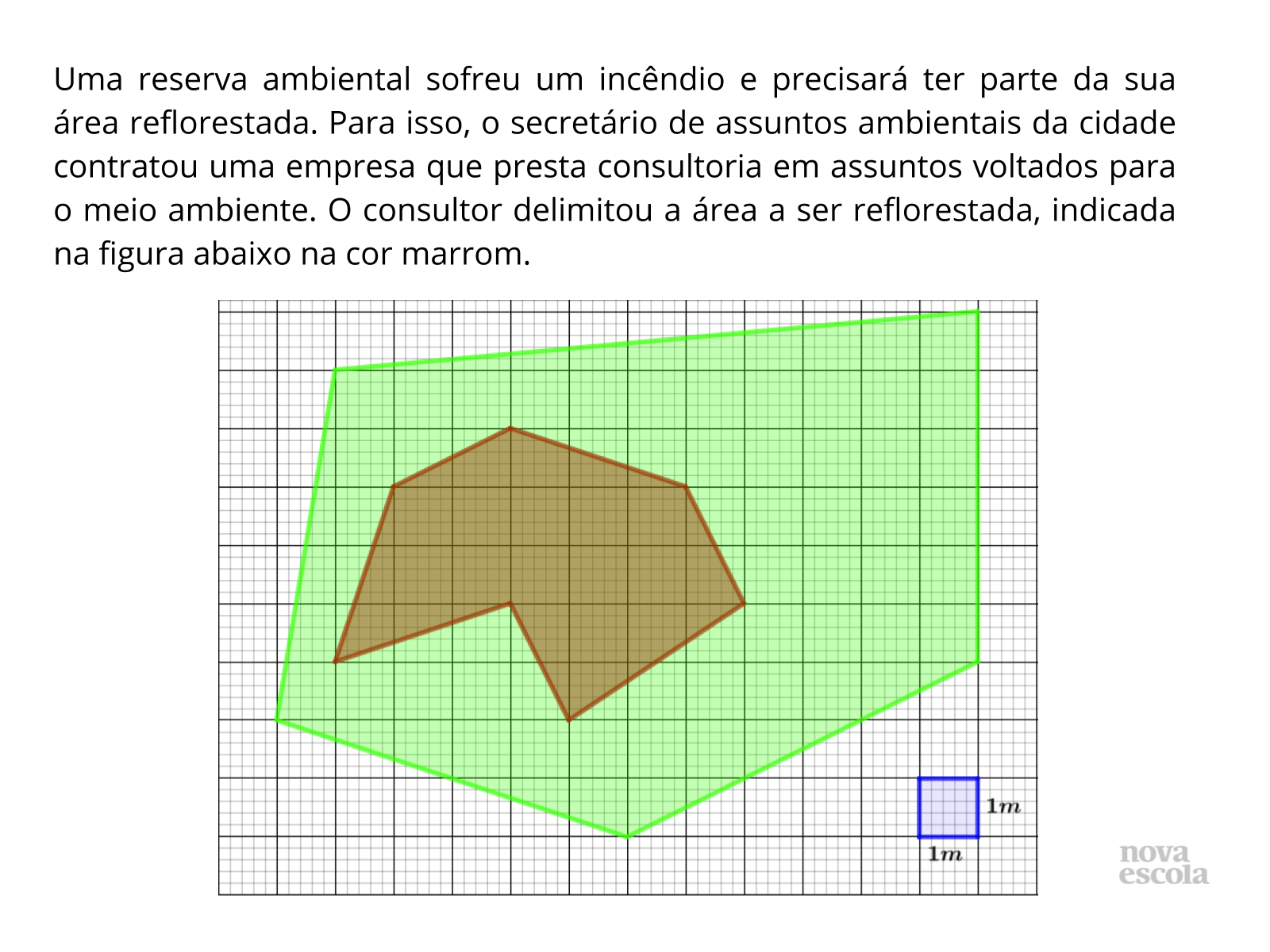
Tempo sugerido: 15 minutos
Orientação: Mantenha a turma em trios e entregue uma cópia da atividade (ou projete na lousa), pedindo para que leiam e reflitam sobre a atividade antes de começar a trocar suas estratégias de resolução. Cada integrante da dupla deverá tentar solucionar o problema da maneira que achar mais conveniente. Caso escolha projetar a atividade sem utilizar a impressão, distribua malhas quadriculadas para que façam seus próprios desenhos. Para isso, permita que usem régua, caso queiram medir sem utilizar a malha quadrada. Deixe que eles tentem sozinhos antes de realizar qualquer interferência. Para resolver possíveis dificuldades, consulte o guia de intervenção e os textos auxiliares.
Propósito: Determinar perímetro e área de uma planta baixa com formato irregular.
Discuta com a turma:
- Os resultados encontrados foram próximos ou não?
- Por que você escolheu esse processo? No que ele se diferencia do seu colega?
- A área a ser replantada será toda preenchida de acordo com relatório? ( verifique painel de soluções)
- A quantidade de sensores foi dividida de maneira igual para todo o terreno? Por quê? (verifique painel de soluções)
Materiais complementares:
Atividade principal (Slides 5 e 6)

Tempo sugerido: 15 minutos
Orientação: Mantenha a turma em trios e entregue uma cópia da atividade (ou projete na lousa), pedindo para que leiam e reflitam sobre a atividade antes de começar a trocar suas estratégias de resolução. Cada integrante da dupla deverá tentar solucionar o problema da maneira que achar mais conveniente. Caso escolha projetar a atividade sem utilizar a impressão, distribua malhas quadriculadas para que façam seus próprios desenhos. Para isso, permita que usem régua, caso queiram medir sem utilizar a malha quadrada. Deixe que eles tentem sozinhos antes de realizar qualquer interferência. Para resolver possíveis dificuldades, consulte o guia de intervenção e os textos auxiliares.
Propósito: Determinar perímetro e área de uma planta baixa com formato irregular.
Discuta com a turma:
- Os resultados encontrados foram próximos ou não?
- Por que você escolheu esse processo? No que ele se diferencia do seu colega?
- A área a ser replantada será toda preenchida de acordo com relatório? ( verifique painel de soluções)
- A quantidade de sensores foi dividida de maneira igual para todo o terreno? Por quê? (verifique painel de soluções)
Discussão das Soluções (slides 13 ao 20)
Tempo sugerido: 10 minutos
Orientação: Projete as imagens e construa um a painel na lousa com as tabelas das resoluções descritas por eles durante a realização da atividade.
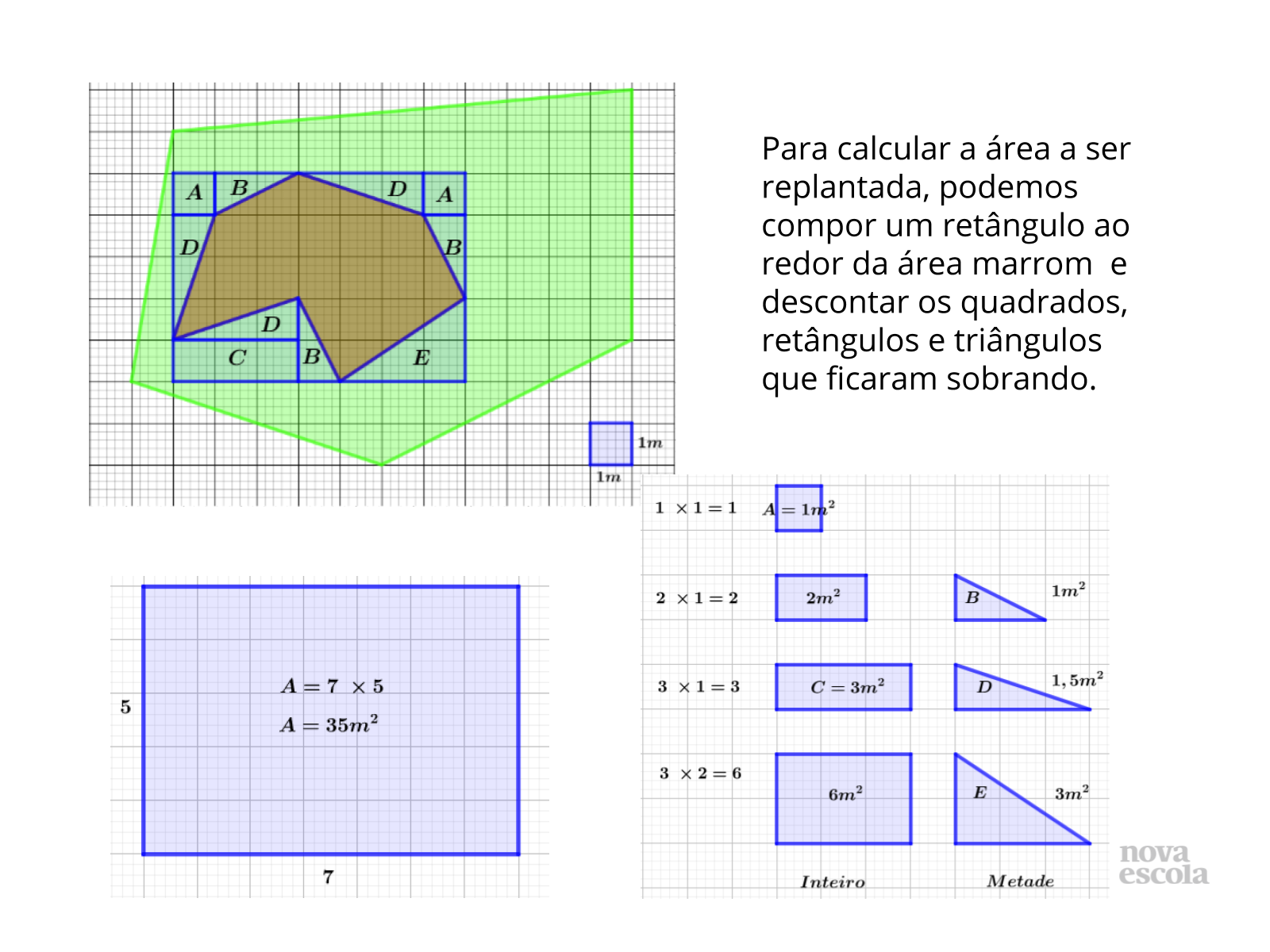
Para calcular a quantidade de mudas é necessário determinar a área da região marrom, por ser um polígono irregular inscrevemos ele numa região retangular (azul) e subdividimos em áreas menores (retângulos, quadrados e triângulos). Tomamos como referência o quadrado da malha para calcular as demais áreas. Os alunos poderão apresentar a união de 2 triângulos iguais para formar retângulos. Consulte.
Propósito: Comparar e associar as diferentes formas de solucionar um mesmo problema.
Discuta com a turma:
- A área a ser replantada será toda preenchida de acordo com relatório? Os alunos deverão se atentar que área a ser preenchida com mudas não é um número inteiro e portanto, a cada 1m² um dos 19 m² receberá 4 mudas o que resulta num total de 76 mudas, a parte restante que representa 0,5 m² será preenchida com 2 mudas, ou seja, a distribuição ocorre de maneira proporcional, logo de acordo com o relatório.
Materiais complementares para impressão:
Discussão das Soluções (slides 13 ao 20)
Tempo sugerido: 10 minutos
Orientação: Projete as imagens e construa um a painel na lousa com as tabelas das resoluções descritas por eles durante a realização da atividade.
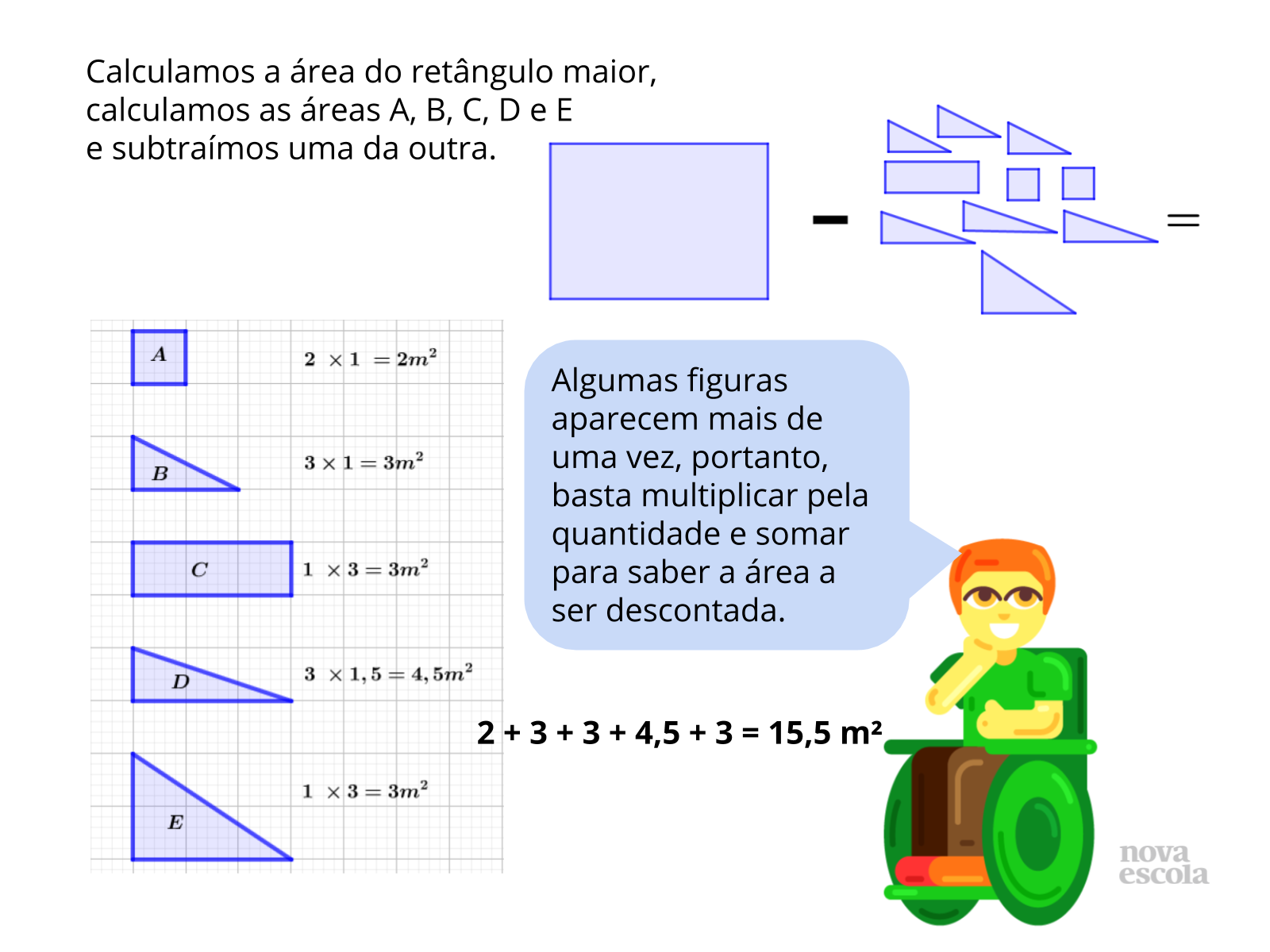
Para calcular a quantidade de mudas é necessário determinar a área da região marrom por ser um polígono irregular inscrevemos ele numa região retangular (azul) e subdividimos em áreas menores (retângulos, quadrados e triângulos). Tomamos como referência o quadrado da malha para calcular as demais áreas. Os alunos poderão apresentar a união de 2 triângulos iguais para formar retângulos. Consulte.
Propósito: Comparar e associar as diferentes formas de solucionar um mesmo problema.
Discuta com a turma:
- A área a ser replantada será toda preenchida de acordo com relatório? Os alunos deverão se atentar que área a ser preenchida com mudas não é um número inteiro e portanto, a cada 1m² um dos 19 m² receberá 4 mudas o que resulta num total de 76 mudas, a parte restante que representa 0,5 m² será preenchida com 2 mudas, ou seja, a distribuição ocorre de maneira proporcional, logo de acordo com o relatório.
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão das Soluções (slides 13 ao 20)

Tempo sugerido: 10 minutos
Orientação: Projete as imagens e construa um a painel na lousa com as tabelas das resoluções descritas por eles durante a realização da atividade.Para calcular a quantidade de mudas é necessário determinar a área da região marrom por ser um polígono irregular inscrevemos ele numa região retangular (azul) e subdividimos em áreas menores (retângulos, quadrados e triângulos). Tomamos como referência o quadrado da malha para calcular as demais áreas. Os alunos poderão apresentar a união de 2 triângulos iguais para formar retângulos. Consulte.
Propósito: Comparar e associar as diferentes formas de solucionar um mesmo problema.
Discuta com a turma:
- A área a ser replantada será toda preenchida de acordo com relatório? Os alunos deverão se atentar que área a ser preenchida com mudas não é um número inteiro e portanto, cada 1m² um dos 19 m² receberá 4 mudas o que resulta em 76 a parte restante que representa 0,5 m² será preenchida com 2 mudas, ou seja, a distribuição ocorre de maneira proporcional, logo de acordo com o relatório.
Materiais complementares para impressão:
Resolução da Atividade Principal
Discussão das Soluções (slides 13 ao 20)
Tempo sugerido: 10 minutos
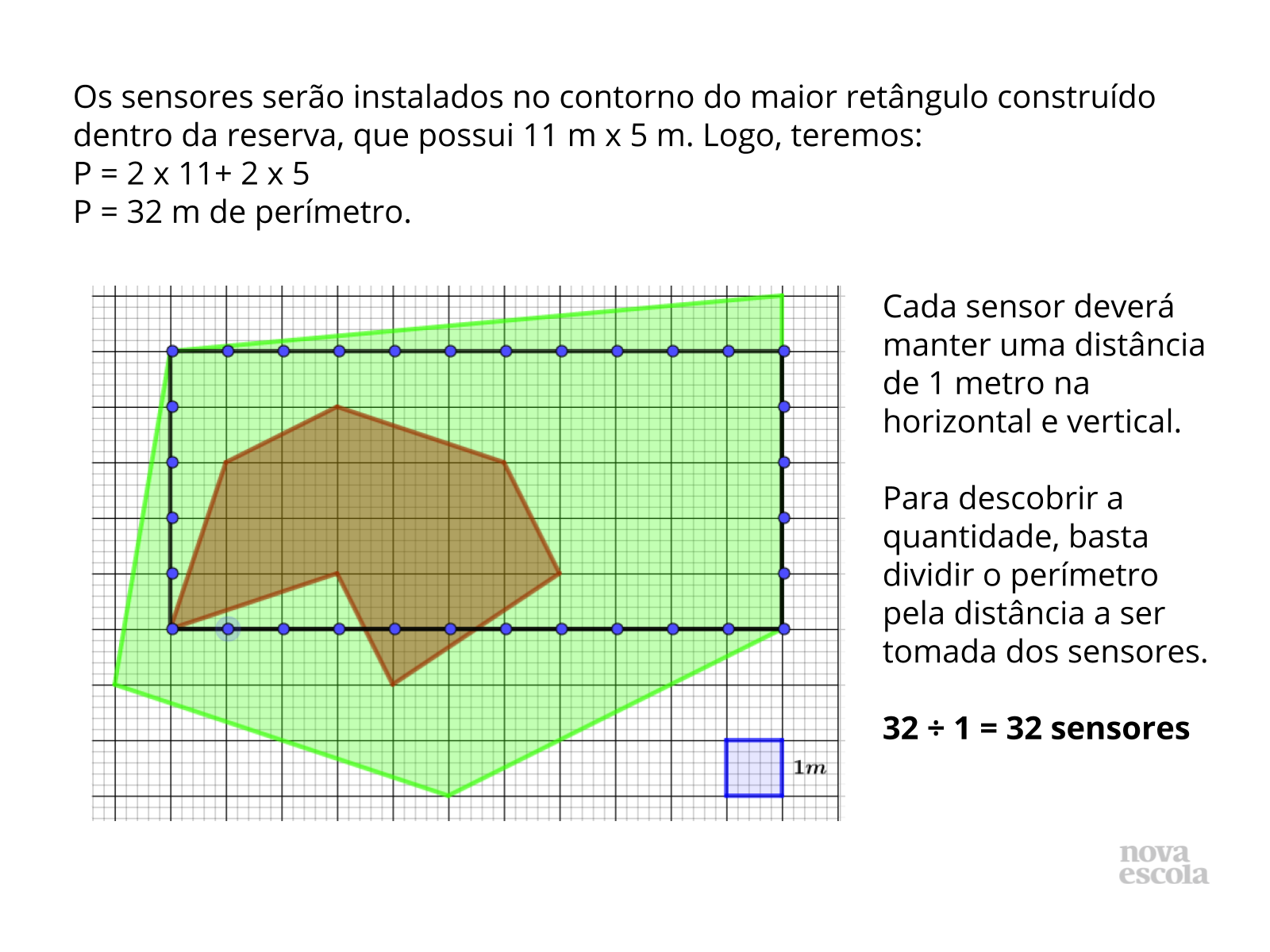
Orientação: Projete as imagens e construa um a painel na lousa com as tabelas das resoluções descritas por eles durante a realização da atividade Os alunos poderão apresentar a resposta apenas pela divisão (slide 19) ou inscrever manualmente na planta (slide 19).
Propósito: Comparar e associar as diferentes formas de solucionar um mesmo problema.
Discuta com a turma:
- A quantidade de sensores foi dividida de maneira igual para todo o terreno? Por quê? Como o critério de distribuição só leva em consideração as distâncias verticais e horizontais e por 1 ser divisor de qualquer número, tendo como resultado o próprio perímetro a distribuição segue de maneira uniforme por todo o contorno. Você pode questionar quanto às distâncias que se formam em diagonais, ou ainda se a distância a ser tomada fosse um outro número o que poderia ocorrer ( em diagonal as distâncias não seriam as mesmas e para garantir a mesma distância de um sensor para outro deveria se adotar quadrados lados divisíveis pelas distâncias a serem tomadas).

Título: Encerramento
Tempo sugerido: 3 minutos.
Orientação: Leia o slide e discuta com a turma.
Propósito: Trazer as impressões dos alunos sobre o tema desenvolvido na aula
Atividade Raio X
Tempo sugerido: 10 minutos.
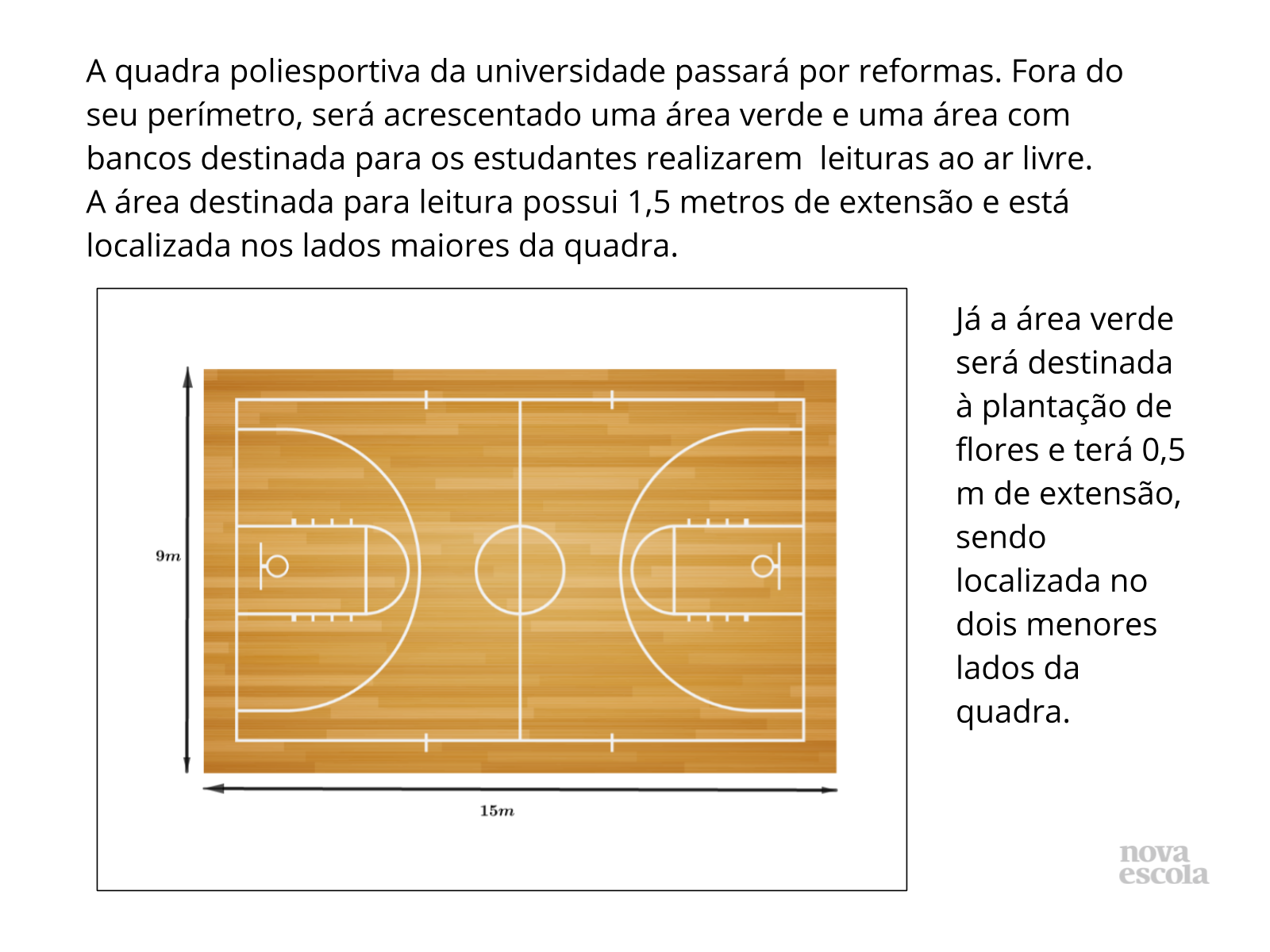
Orientação: Para esta atividade é necessário papel quadriculado e régua, além da atividade impressa ou projetada. Mantenha os trios e peça para que discutam as possíveis maneiras de resolver a atividade anotando os processos de soluções em seus cadernos para socialização com a turma. Você poderá montar um painel e compartilhar as resoluções da mesma maneira que fez durante a atividade principal. Para essa atividade é particularmente importante que, mesmo discutindo em trios, a resolução seja escrita individualmente.
Propósito: Delimitar áreas e perímetros a partir de um problema para verificar o aprendizado dos alunos
Discuta com a turma:
- Como estabelecer a posição da área verde e dos bancos?
- Como encontraram a quantidade máxima de bancos que cabem?
- As linhas de demarcação de uma quadra possuem simetria?
- Por que essas regiões demarcadas numa quadra são importantes?
- Um atleta precisa ter noção do espaço que ele pode utilizar em quadra?
Materiais complementares para impressão:
Atividade Raio X: Reformando a Quadra.

Tempo sugerido: 10 minutos.
Orientação: Para esta atividade é necessário papel quadriculado e régua. Mantenha as duplas e peça para que discutam as possíveis maneiras de resolver a atividade anotando os processos de soluções em seus cadernos para socialização com a turma. Você poderá montar um painel e compartilhar as resoluções da mesma maneira que fez durante a atividade principal.
Propósito: Delimitar áreas e perímetros a partir de um problema.
Discuta com a turma:
- Como estabelecer a posição da área verde e dos bancos?
- Como encontraram a quantidade máxima de bancos que cabem?
- As linhas de demarcação de uma quadra possuem simetria?
- Por que essas regiões demarcadas numa quadra são importantes?
- Um atleta precisa ter noção do espaço que ele pode utilizar em quadra?
Materiais complementares para impressão:
Resolução da Atividade Complementar
Sugestão de adaptação para ensino remoto
Código do plano
MAT6_21GRM04
Recursos
- Necessários: Caderno, lápis, borracha, malha quadriculada (0,5 x 1), régua, lápis de cor
- Opcionais: Google sala de aula, Meet
Plantas baixas: https://pt.khanacademy.org/math/6-ano-matematica/grandezas-e-medidas/planta-baixa-e-vistas-areas/v/plantas-baixas
Para este plano, foque na etapa Retomada
Retomada
Você pode fazer uma sala de aula invertida. Envie com antecedência para os alunos o arquivo da Retomada (WhatsApp). Peçam que desenhem a malha usando as linhas do caderno. O objetivo da aula é ler a planta identificando suas medidas de perímetro e área. Oriente-os que pensem na atividade antes do dia do encontro marcado seguindo as seguintes as orientações:
a) desenhar a planta inteira da praça;
b) determinar a quantidade de cerca necessária para área verde;
c) determinar as medidas de áreas dos espaços nas cores cinza e verde.
Observando a planta da praça enviada, os alunos precisam desenhar a planta completa e determinar o comprimento da cerca e a área a ser coberta pelo piso antiderrapante. Instigue-os a fazer antes da aula. É importante essa autonomia dos alunos. O erro e as tentativas faz parte da aprendizagem. Deixe um canal de comunicação sempre aberto entre vocês para possíveis dúvidas ou encaminhamentos. No dia do encontro marcado (Meet, Hangouts, Zoom, Teams), deixe que os alunos compartilhem como pensaram e, se tiver algum registro, esse é o momento de mostrar. Retome as perguntas direcionadas e converse sobre cada uma delas. É importante saber quais as possíveis dúvidas e/ou questionamentos dos alunos.
Compartilhe a tela com o desenho de cada parte, mostrando a decomposição e o cálculo do perímetro. Diga quais são as opções: eles podem contar os retângulos e calcular a área; calcular a área verde e a área cinza ou então subdividir em retângulos. É importante dizer e mostrar que não existe uma única maneira de resolver esse problema. Eles podem pensar em outros recortes. Estimular a desenhar e a fazer por si só, é um grande passo para a aprendizagem significativa. Aproveite, e converse sobre simetria da figura. Questione se vale a pena saber se a figura a ser desenhada é simétrica a que já existia. Faça boas perguntas com foco na aula.
Se sua aula fora assíncrona, deixe a tarefa na escola ou envie pelo WhatsApp. Grave um áudio explicando e peçam que enviem para você combinando um retorno de devolutiva. Nesse retorno, você pode enviar o print com a planta para que eles comparem com a deles e colem no seu caderno.
Sugira aos alunos que tenham acesso à internet os vídeos da Plataforma Khan Academy:
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados nessa fase com outras funções em casa. Peça às famílias, que oportunamente, auxiliem na leitura das comandas e no envio das soluções, conforme os combinados com o professor. É importante que as famílias acompanhem as atividades nos canais de comunicação estabelecidos entre vocês. Convide um familiar para que possa assistir aos vídeos com você e ajudar a construir a planta da sua casa. Que tal? Comece a medir os comprimentos e largura de cada cômodo. Fica a dica!!!
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autora: Elizabeth Bento
Mentora: Maria Aparecida Nemet
Revisor: Rodrigo Morozetti Blanco
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF06MA26) Interpretar, descrever e desenhar plantas baixas simples de residências e vistas aéreas.
Habilidades necessárias
Trabalhar com malhas retangulares e triangulares, decompor um polígono em regiões mais simples (quadrado, retângulo e triângulo)
Objetivos específicos
Determinar áreas e perímetros de plantas irregulares.
Conceito-chave
Planta baixa, perímetro, área.
Recursos necessários
-Malha retangular;
-Sulfite;
-Lápis de cor;
-Régua.