Guia de Intervenção
Plano de Aula
Plano de aula: Quantas pessoas podem participar de um evento?
Plano 3 de uma sequência de 5 planos. Veja todos os planos sobre Medição de superfícies
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alex de Cassio Macedo
Mentora: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF07MA26) Resolver e elaborar problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas.
Objetivos específicos
Calcular as medidas de superfície a partir da decomposição em triângulos e quadriláteros.
Conceito-chave
Calcular área por meio de decomposição.
Recursos necessários
- Atividades impressas em folhas.
- Régua, lápis, borracha, caderno.
- Giz ou fita crepe.
Habilidades BNCC:
Objetivos de aprendizagem
Calcular as medidas de superfície a partir da decomposição em triângulos e quadriláteros.
Resumo da aula
 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo da aula

Tempo sugerido: 2 minutos.
Orientação: Neste primeiro momento explique o objetivo da aula de maneira clara e sucinta, argumente que a partir desta aula o aluno(a) será capaz de calcular medidas de superfície ou áreas em diversas situações, decompondo-as em figuras mais simples e conhecidas.
Propósito: Compartilhar o objetivo da aula e motivá-los ao estudo.
Discuta com a turma:
- É claro o sentido da palavra decomposição?
- Segundo o dicionário : Decompor é separação dos elementos formadores ou constituintes de algo.
- Peça que eles exemplifiquem uma figura cuja a expressão de área é desconhecida por eles.
Aquecimento
Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
Propósito: Promover uma retomada de conceitos relacionados ao cálculo de áreas.
Discuta com a turma:
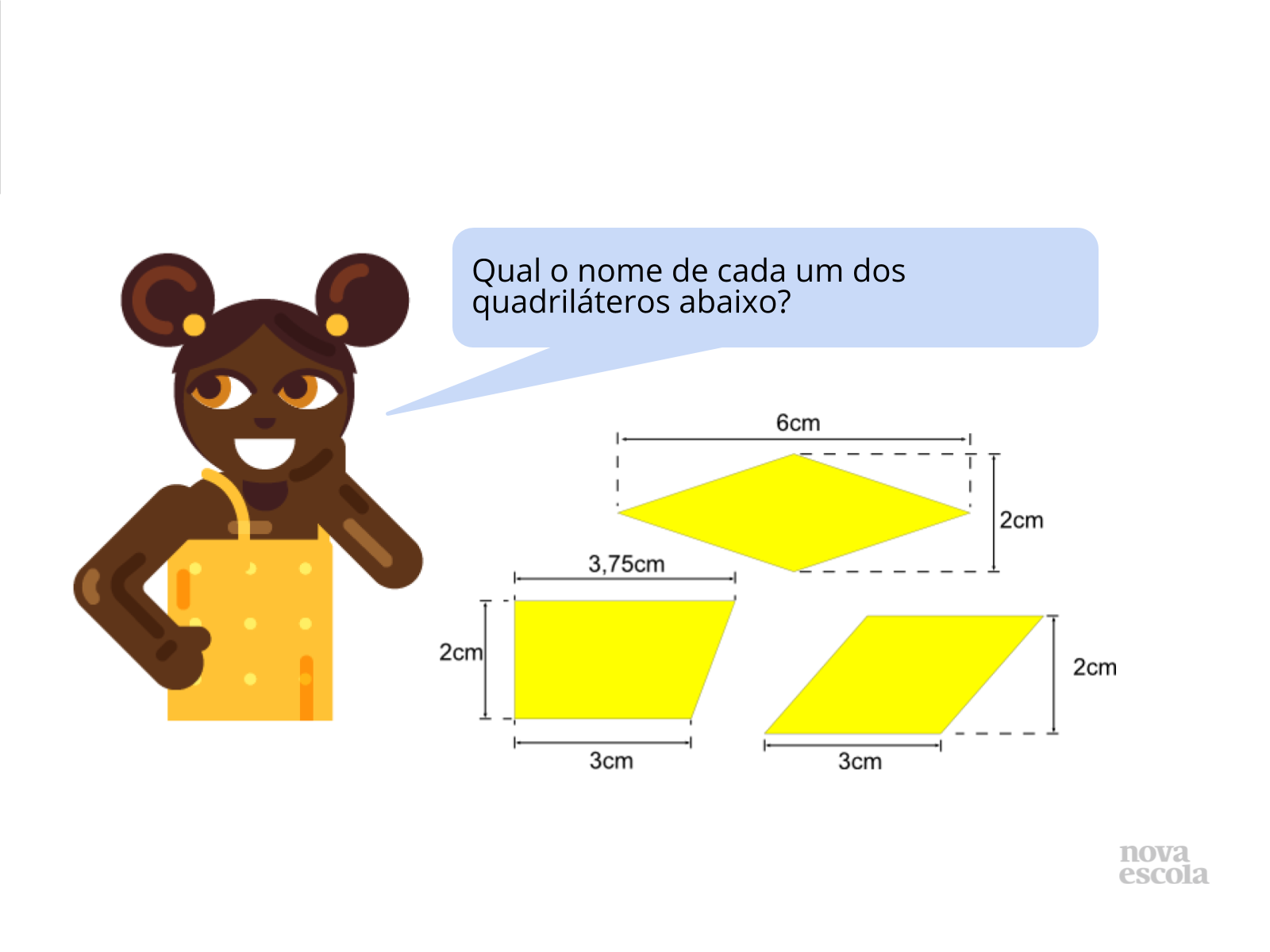
- Qual a diferença entre as figuras apresentadas?
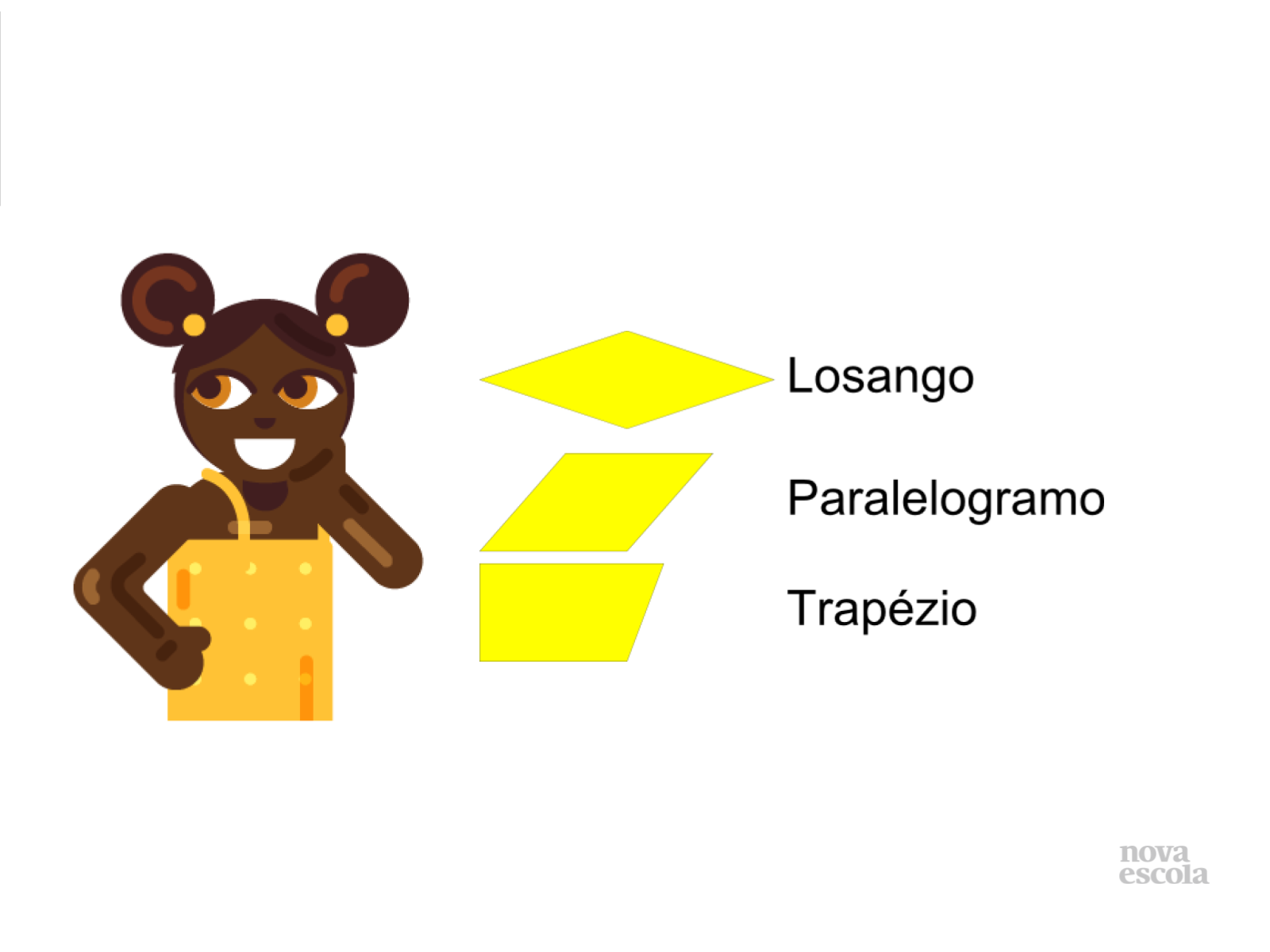
- Apesar de serem quadriláteros, cada uma delas possui características diferentes:
- Os paralelogramos são quadriláteros que possuem lados paralelos dois a dois, esta característica torna o losango um tipo de paralelogramo, porém o losango obrigatoriamente deve possuir lados iguais, já o paralelogramo não.
- Já o trapézio não possui lados paralelos dois a dois.
Aquecimento
Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
Propósito: Promover uma retomada de conceitos relacionados ao cálculo de áreas e de figuras planas.
Discuta com a turma:
- Qual a diferença entre as figuras apresentadas?
- Apesar de serem quadriláteros, cada uma delas possui característica diferentes:
- Os paralelogramos são quadriláteros que possuem lados paralelos dois a dois, esta característica torna o losango um tipo de paralelogramo, porém o losango obrigatoriamente deve possuir lados iguais, já o paralelogramo não.
- Já o trapézio não possui lados paralelos dois a dois.
Aquecimento
Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
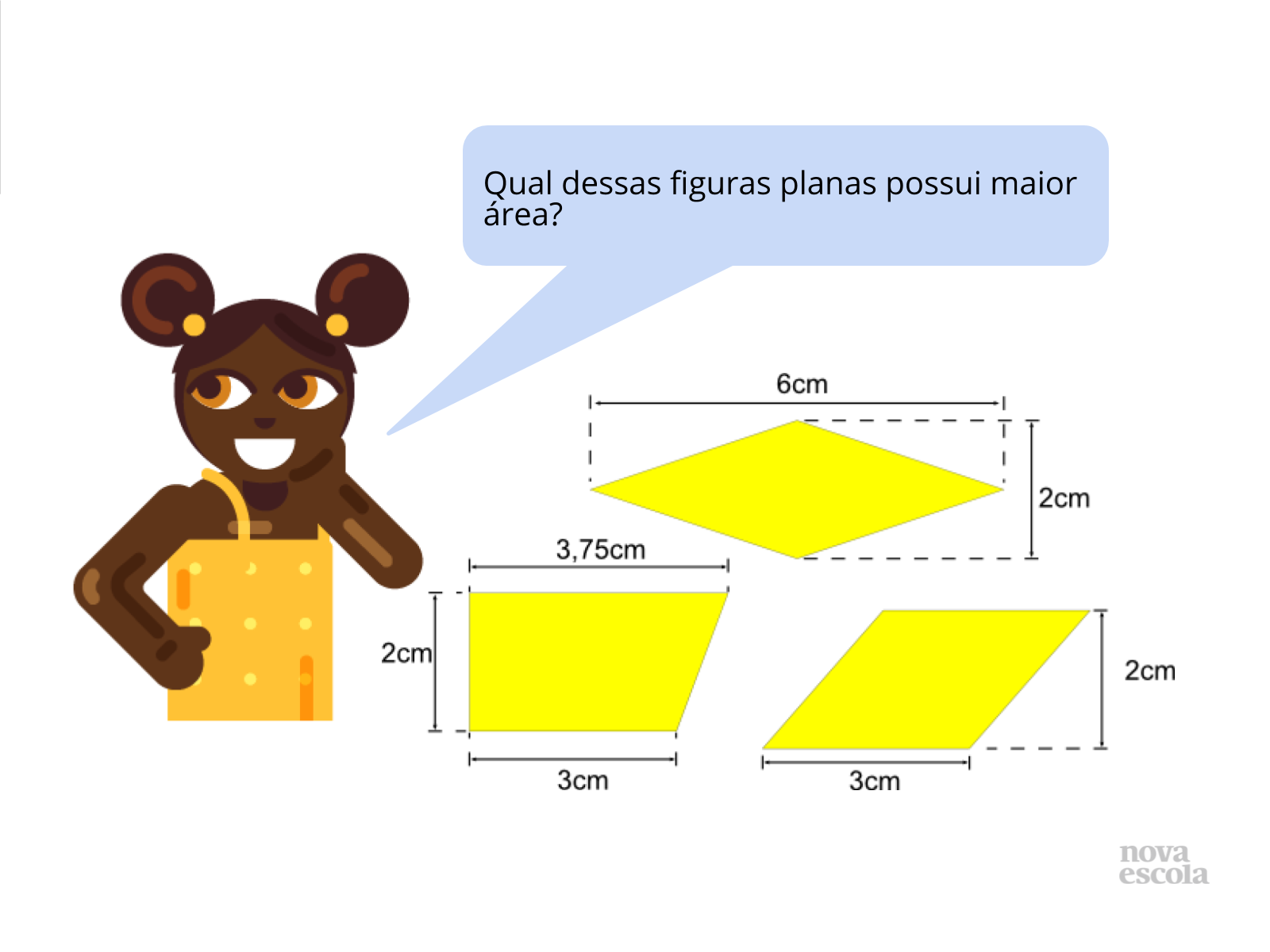
Propósito: Provocar um momento de observação e dedução das áreas das figuras por estimativa.
Discuta com a turma:
- Qual figura possui maior área (sem fazer cálculos! )? Como você chegou a esta conclusão?
Aquecimento
Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
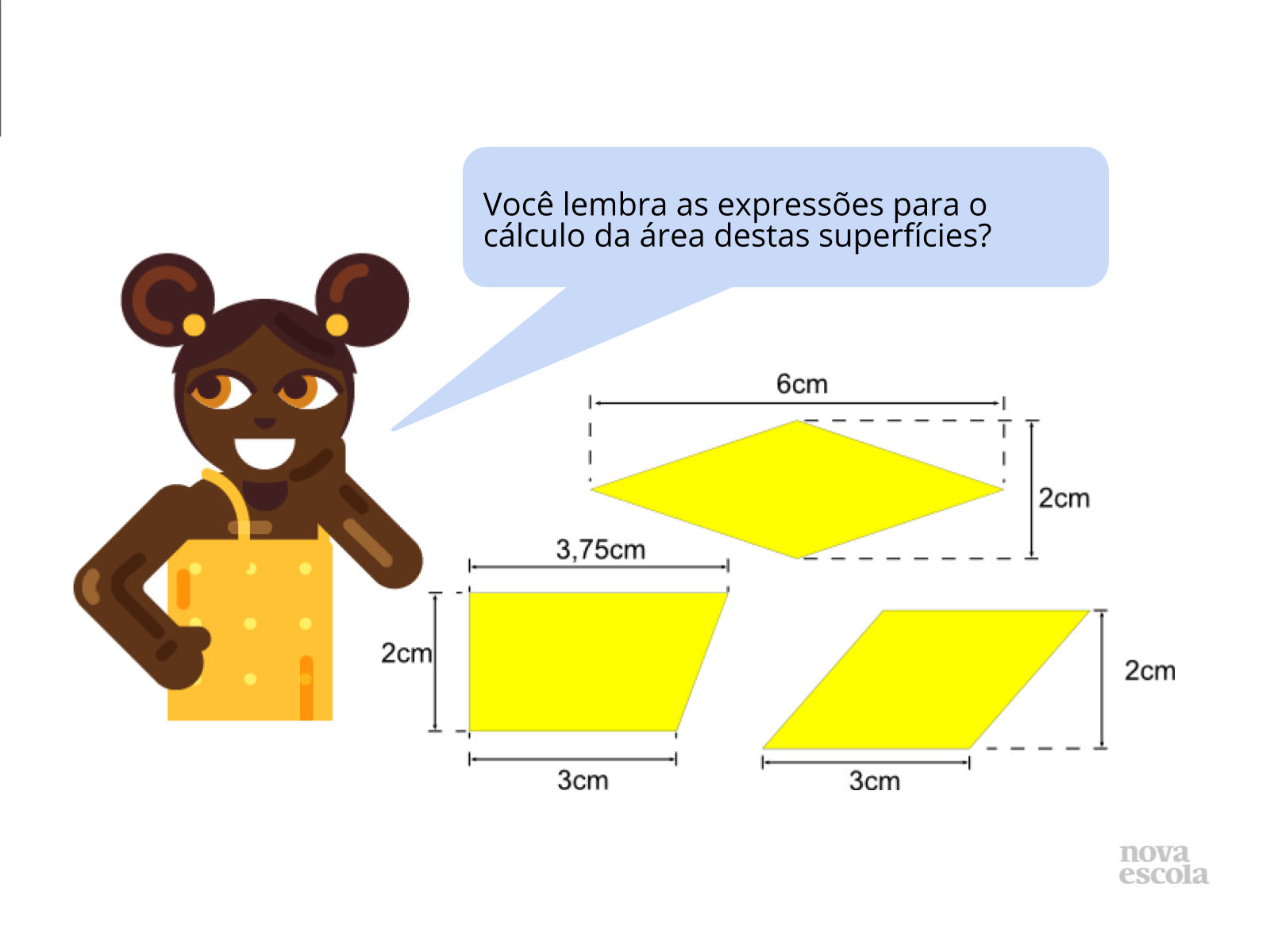
Propósito: Relembrar as expressões que calculam a área de cada uma das figuras apresentadas.
Discuta com a turma:
- Quais as expressões que calculam essas áreas?
Aquecimento
Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
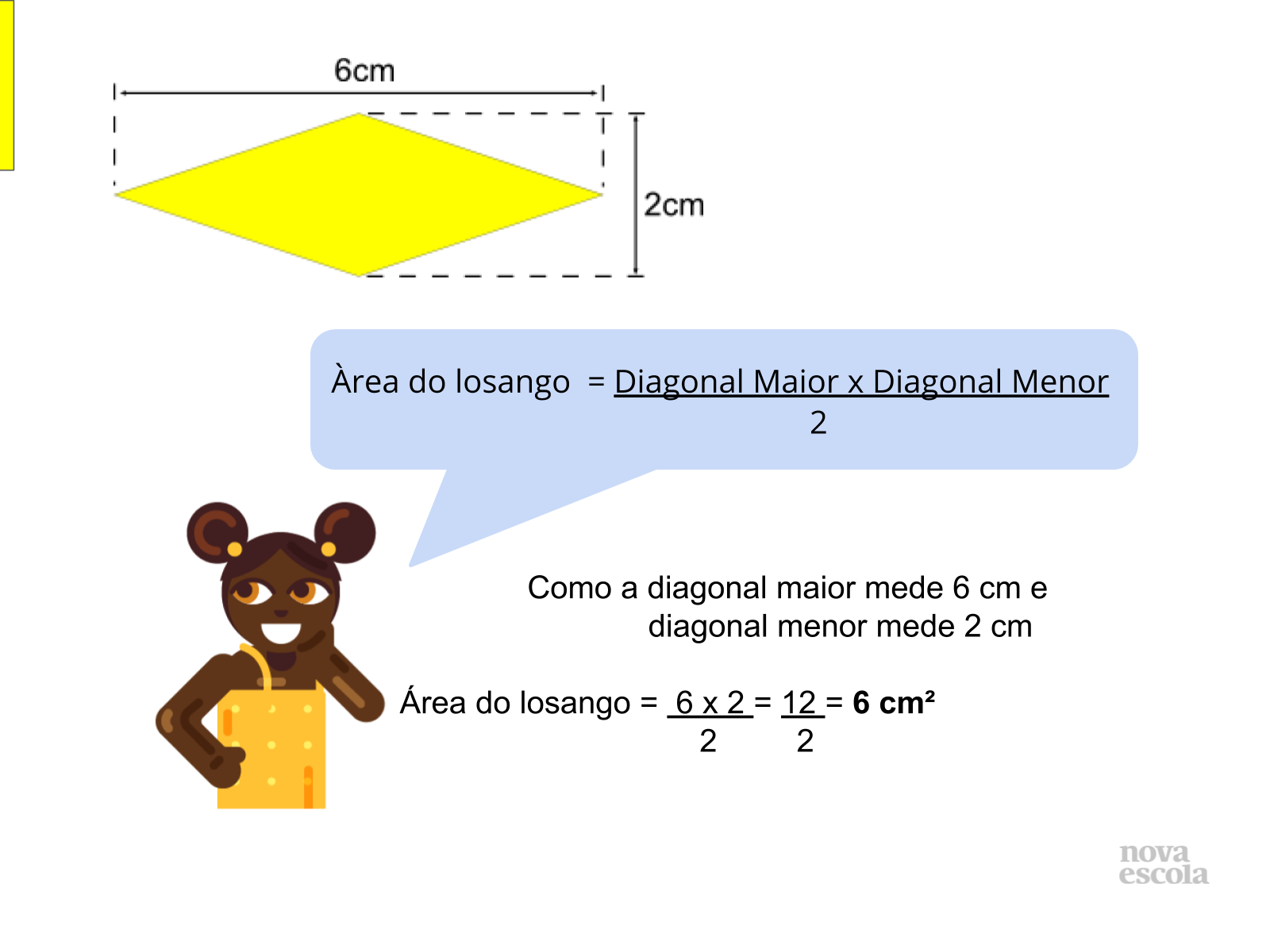
Propósito: Relembrar a expressão que calcula a área do losango.
Discuta com a turma:
- Quais são as dimensões necessárias que calculam a área do losango?
- Diagonal Maior e Diagonal menor
- Como pode ser utilizada esta expressão?
- Substituindo as medidas e realizando os cálculos.
Aquecimento

Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
Propósito: Relembrar a expressão que calcula a área do paralelogramo.
Discuta com a turma:
- Quais são as dimensões necessárias para calcular a área do paralelogramo?
- Comprimento e Largura
- Como pode ser utilizada esta expressão?
- Substituindo as medidas e realizando os cálculos.
Aquecimento
Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
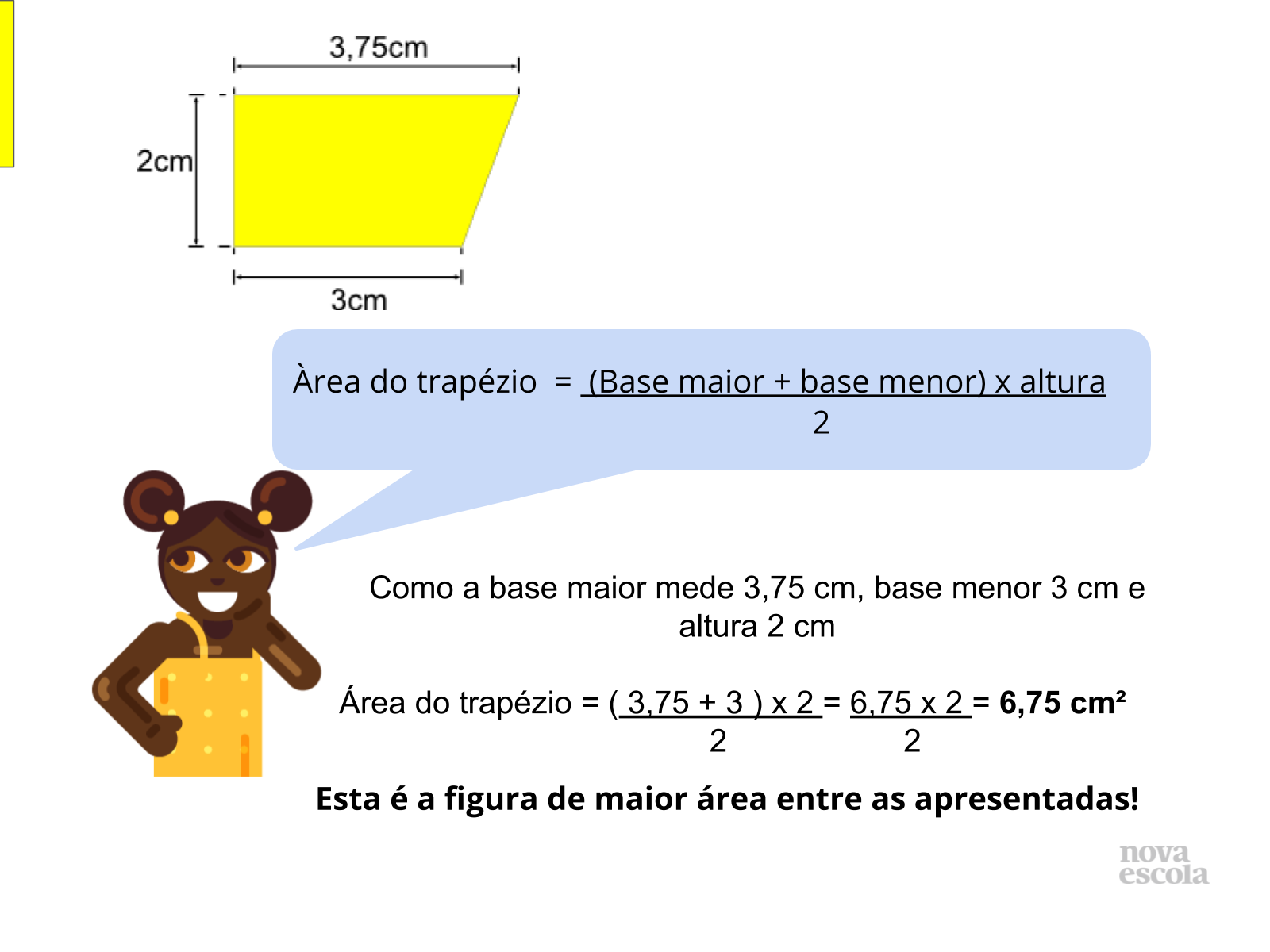
Propósito: Relembrar a expressão que calcula a área do trapézio.
Discuta com a turma:
- Quais são as dimensões necessárias para calcular a área do trapézio?
- Base Maior, Base Menor e altura
- Como pode ser utilizada esta expressão?
- Substituindo as medidas e realizando os cálculos.
Aquecimento

Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
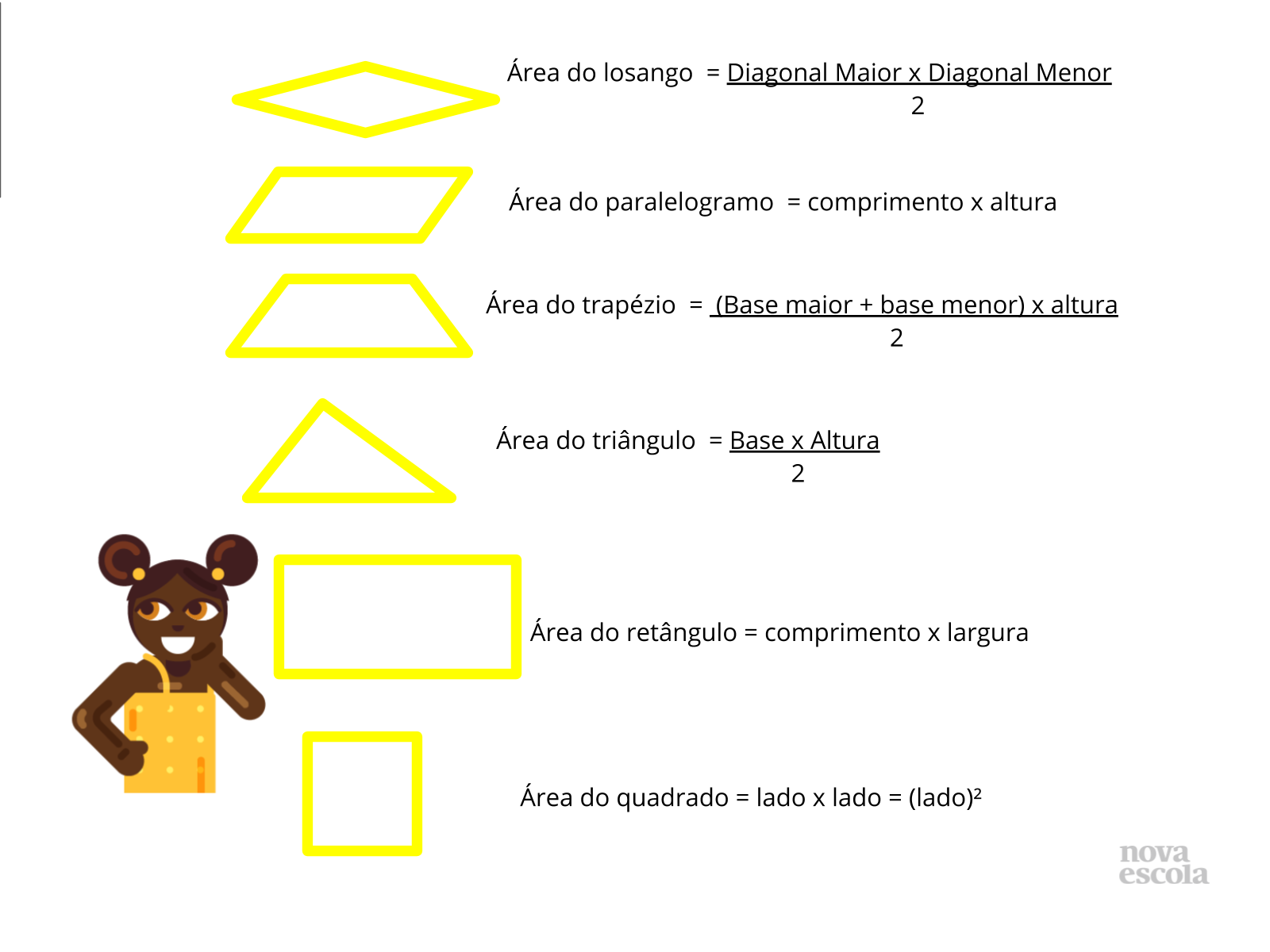
Propósito: Registro das expressões para uso na atividade principal.
Aquecimento
Tempo previsto: 10 minutos (slide 3 ao slide 11).
Orientações: Neste momento é importante retomar os conceitos de área do triângulo e dos quadriláteros, cuide para não revelar a resolução préviamente do problema proposto.
Propósito: Registro das expressões para uso na atividade principal.
Você pode também imprimir este formulário e entregar para os alunos colarem no caderno. Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Atividade Principal

Tempo previsto: 15 minutos (slide 12 ao slide 15).
Orientações: A atividade principal apresenta um problema prático que exigirá o cálculo da área de uma figura complexa cuja expressão do cálculo de sua área não é conhecida, por isso os alunos devem ser motivados a decompô-la em figuras conhecidas, além disso terão que decidir de maneira intuitiva quantas pessoas podem ocupar uma área de um metro quadrado confortavelmente.
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Propósito: Ler, interpretar e esclarecer os detalhes do problema.
Discuta com a turma:
- O que é necessário saber para resolver o problema?
- Chamar atenção para o fato de determinar a densidade de pessoas no ambiente (pessoas por metro quadrado)
- Subdividir a figura em quadriláteros e triãngulos conhecidos.
Atividade Principal
Tempo previsto: 15 minutos (slide 12 ao slide 15).
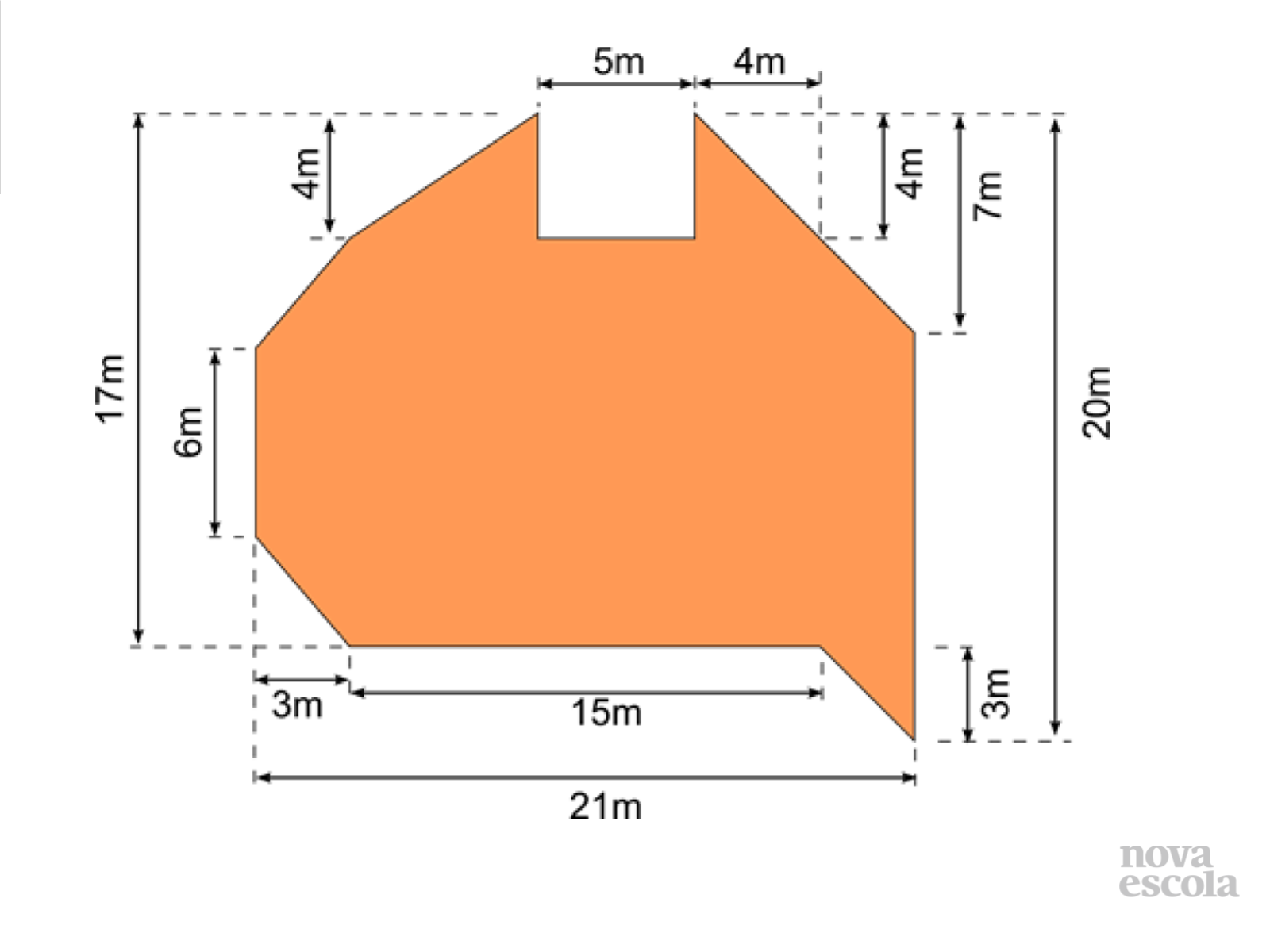
Orientações: Esta é a figura que representa o pátio onde ocorrerá o evento. È importante nesse momento motivar os alunos a pensarem em estratégias de como resolver o problema. È também fundamental chamar atenção dos alunos quanto às dimensões da figura e como utilizá-las.
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Propósito: Apresentar a figura que representa a área em questão .
Discuta com a turma:
- Qual será a maneira mais fácil de calcular a área em questão?
Atividade Principal

Tempo previsto: 15 minutos (slide 12 ao slide 15).
Orientações: Neste momento é importante deixar que os alunos pensem em estratégias para determinar a quantidade de pessoas por metro quadrado, note que esta informação pode mudar drasticamente o resultado do problema.
Propósito: Permitir que os alunos pensem em estratégias de como determinar a densidade no evento .
Atividade Principal
Tempo previsto: 15 minutos (slide 12 ao slide 15).
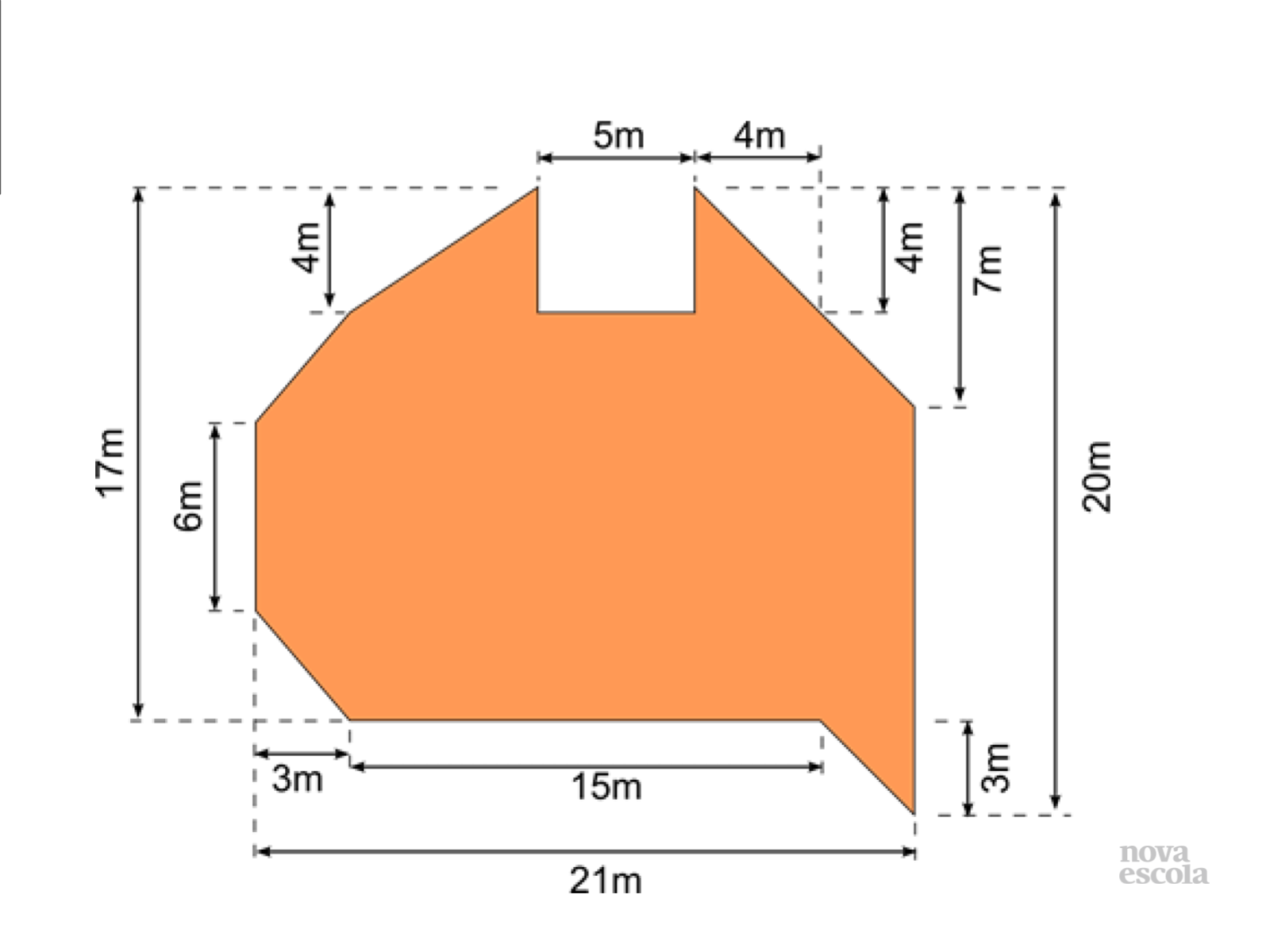
Orientações: Deixar esta imagem projetada durante a resolução da atividade para possíveis hipóteses de solução
Propósito: Provocar a discussão e hipóteses de resolução .
Discussão da solução

Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução

Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no Guia de Intervenções Aqui!
Propósito: Provocar a discussão de soluções .
Discussão da solução

Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução

Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução

Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no Guia de Intervenções Aqui!
Propósito: Provocar a discussão de soluções .
Discussão da solução
Tempo previsto: 10 minutos (slide 16 ao slide 30).
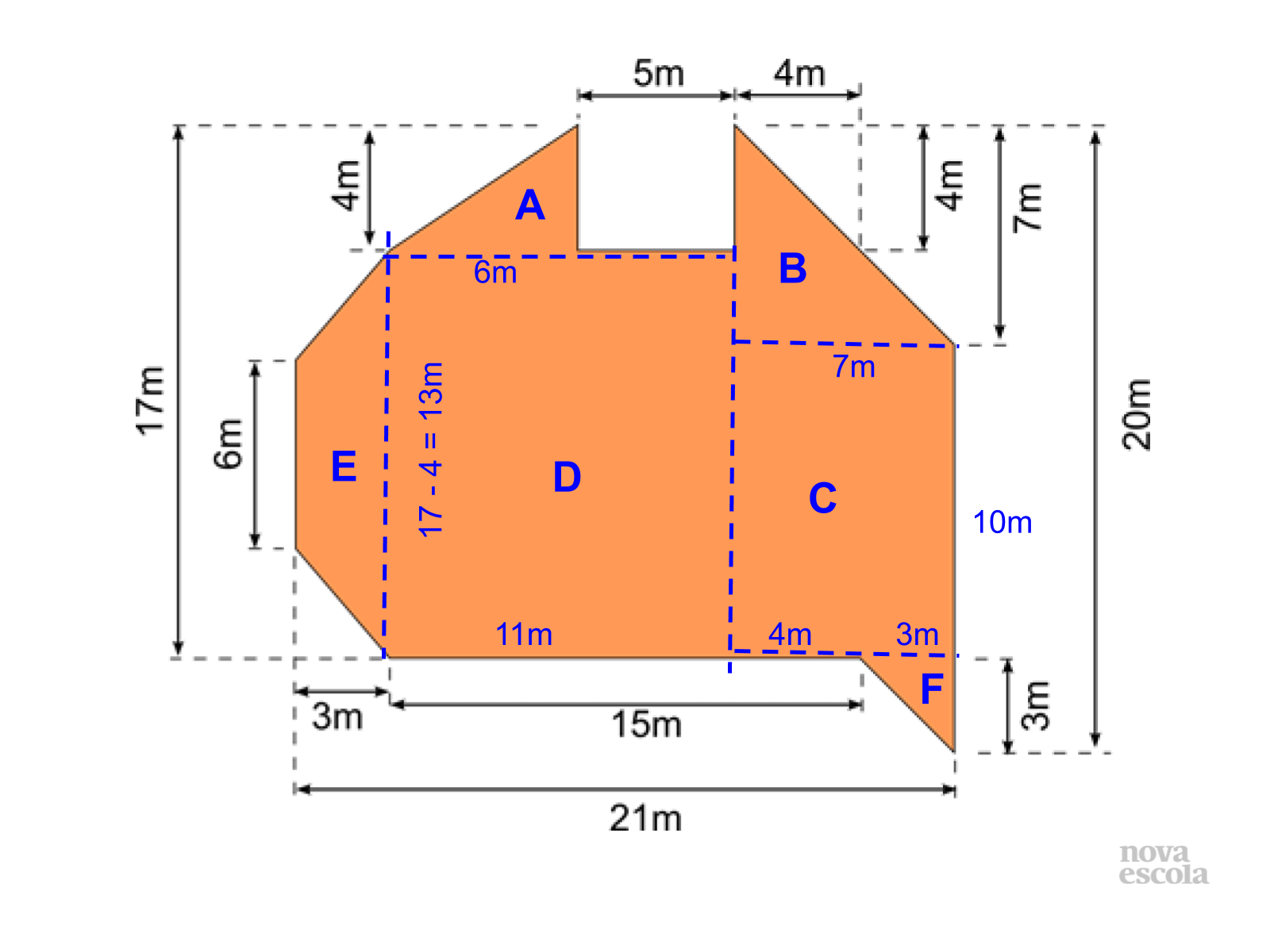
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução

Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução
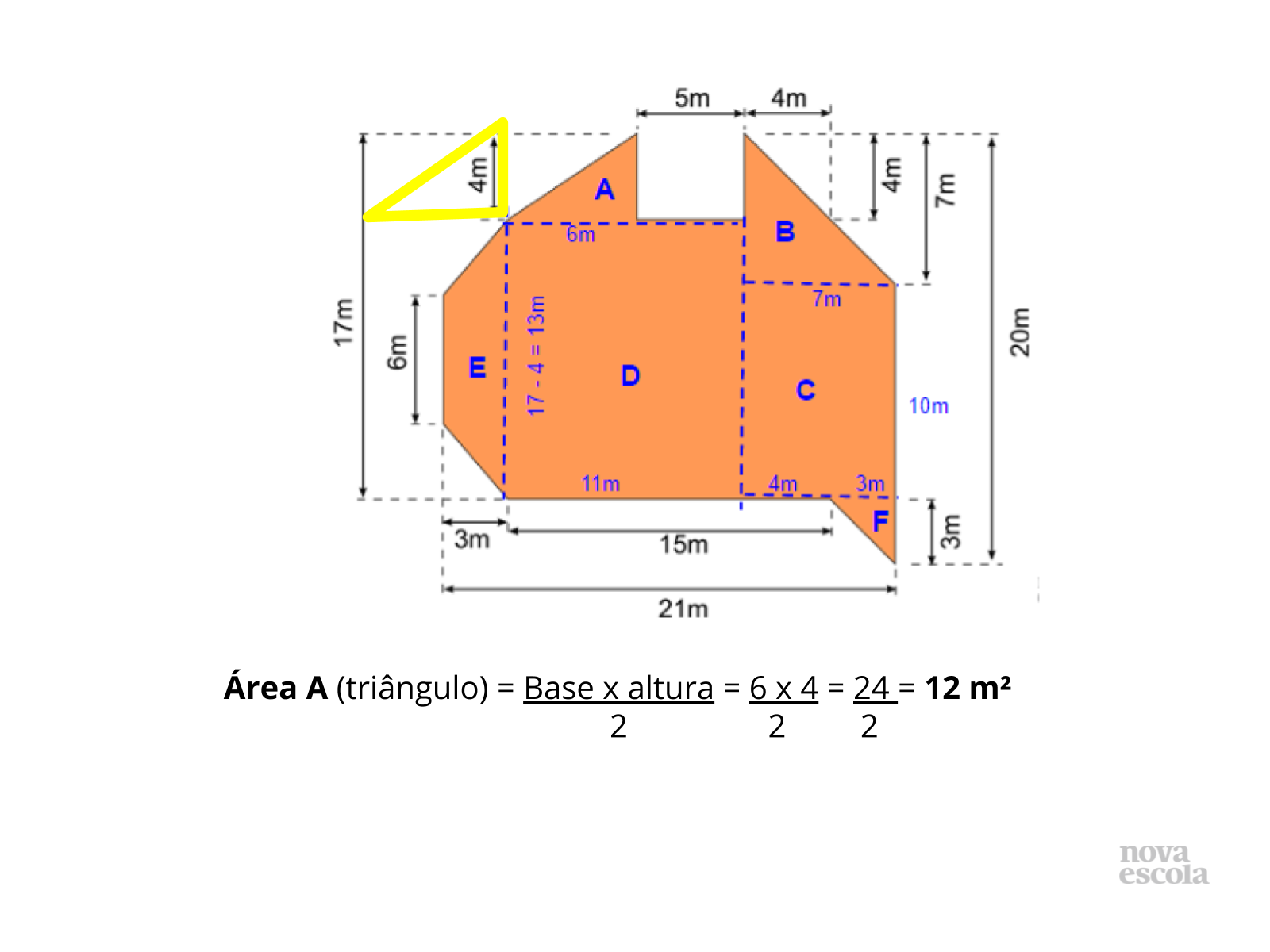
Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução
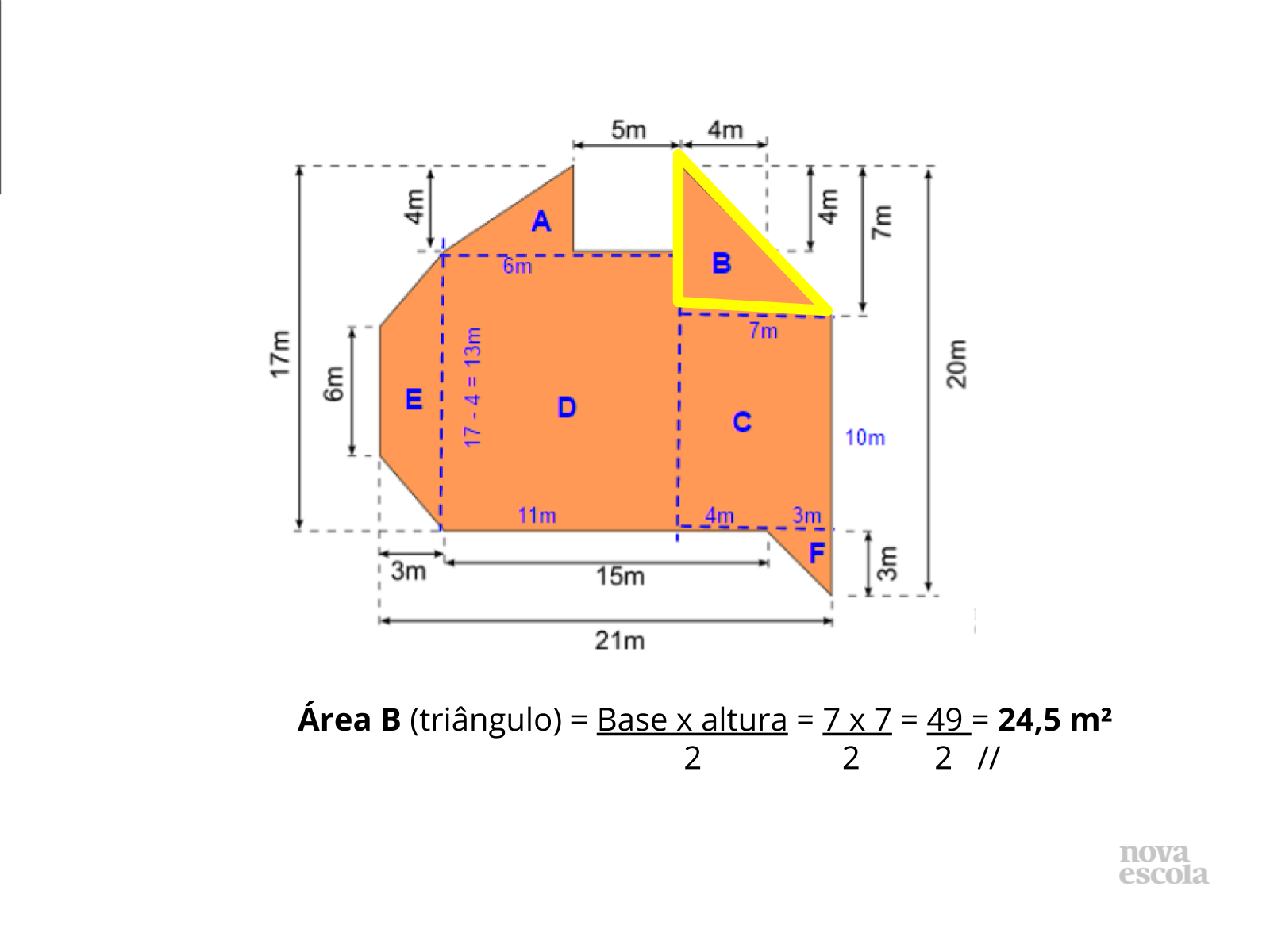
Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no Guia de Intervenções Aqui!
Propósito: Provocar a discussão de soluções .
Discussão da solução
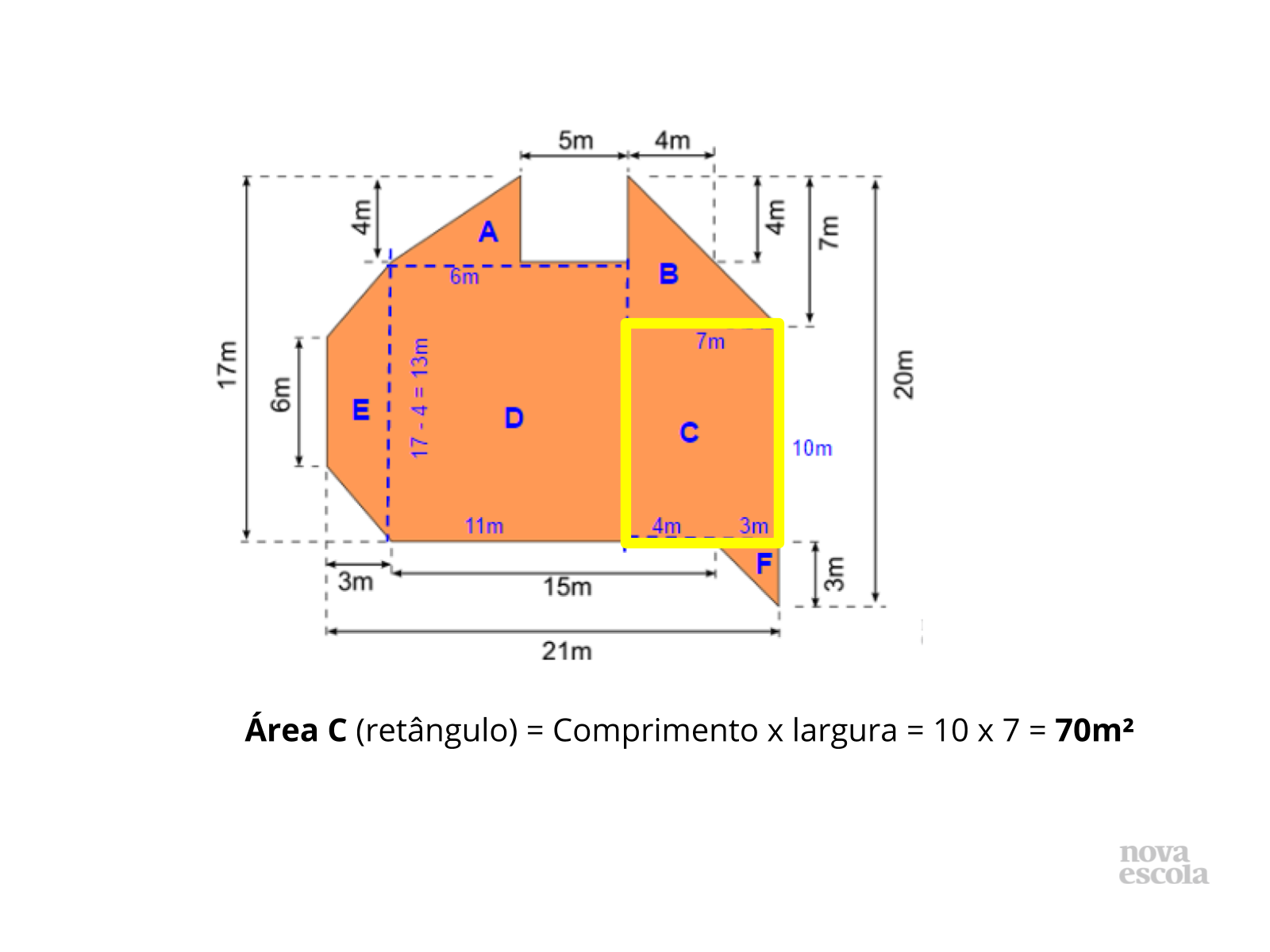
Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução
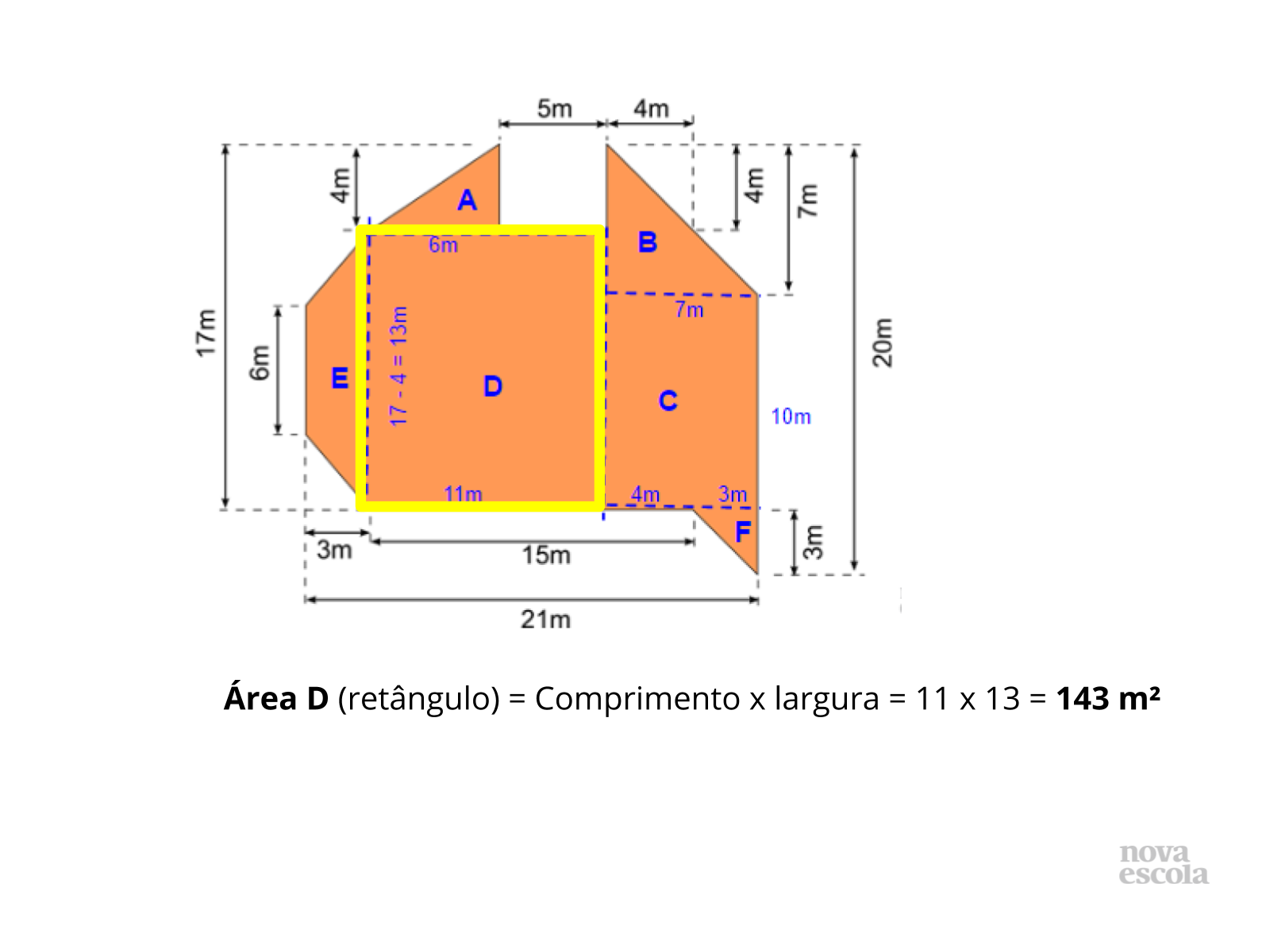
Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução
Tempo previsto: 10 minutos (slide 16 ao slide 30).
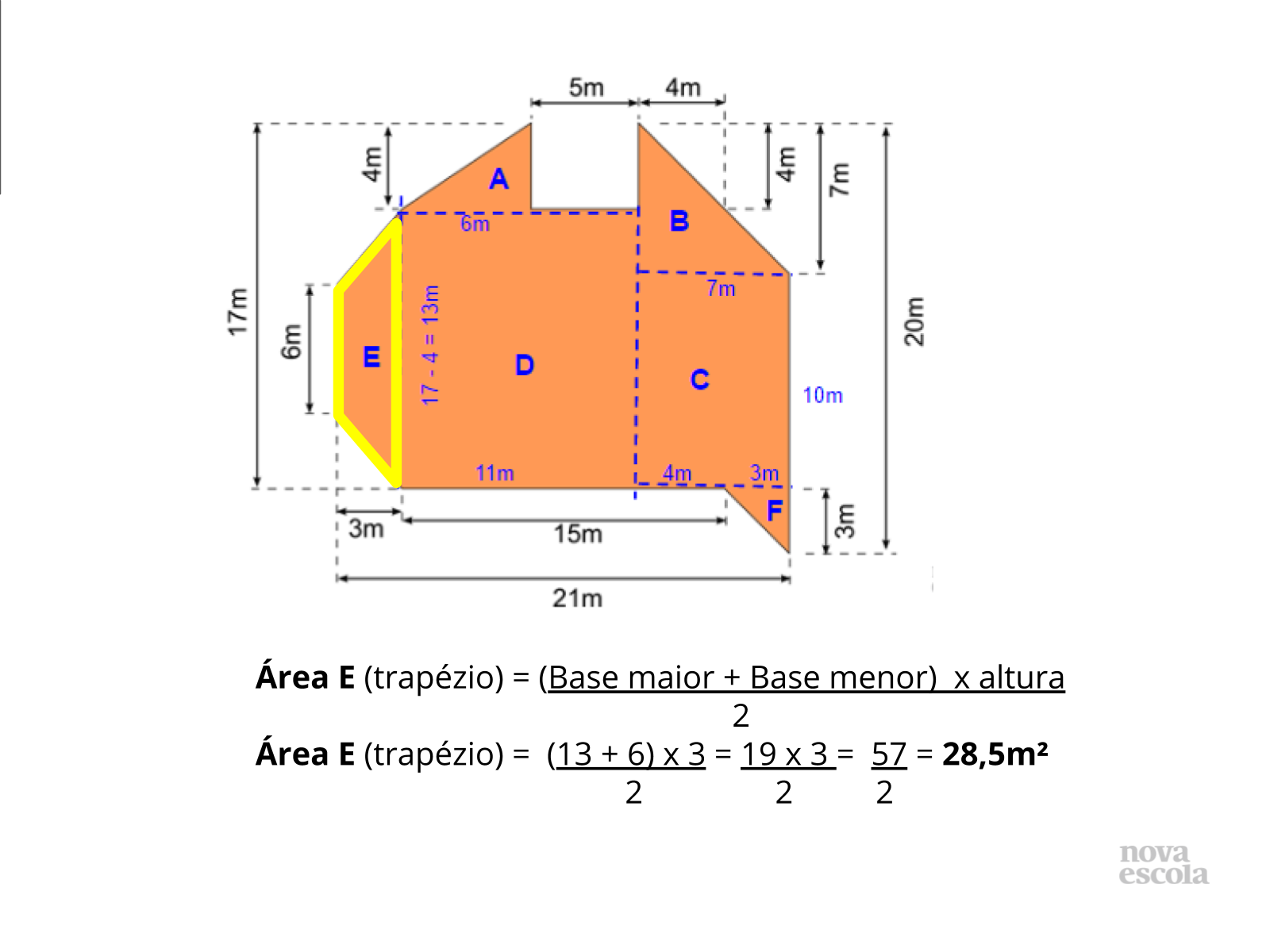
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução
Tempo previsto: 10 minutos (slide 16 ao slide 30).
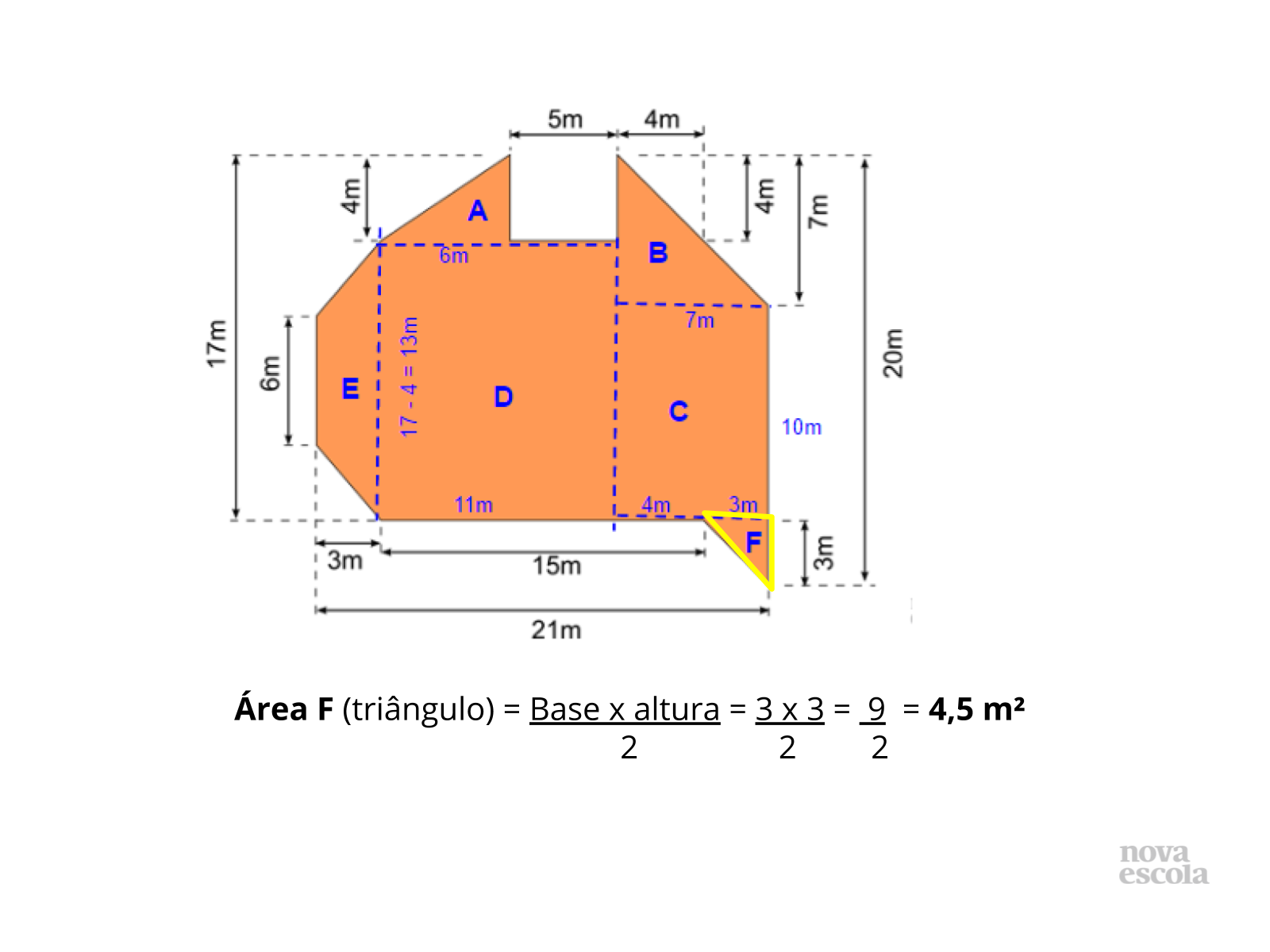
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Propósito: Provocar a discussão de soluções .
Discussão da solução

Tempo previsto: 10 minutos (slide 16 ao slide 30).
Orientações: Os próximos slides vão discutir uma possibilidade de resolução, é importante que o professor apresente a solução apresentada como uma provocação para que os alunos mostrem como resolveram, tanto os alunos que chegaram a uma solução correta quanto aqueles que erraram ou não chegaram a uma solução.
Possíveis situações e dúvidas podem ser vistas no Guia de Intervenções Aqui!
Propósito: Provocar a discussão de soluções .
Discussão da solução

Tempo previsto: 15 minutos (slide 12 ao slide 15 ).
Orientações: Esta é a figura que representa o pátio onde ocorrerá o evento. È importante nesse momento motivar os alunos a pensarem em estratégias de como resolver o problema. È também fundamental chamar atenção dos alunos quanto às dimensões da figura e como utilizá-las.
Propósito: Discutir o valor fracionário do resultado da área.
Discuta com a turma:
- O resultado encontrado é razoável, como lidar com esse 282,5?
- Pode-se utilizar dois recursos para determinar um valor inteiro para o problemas, o arredondamento e o truncamento.
- No arredondamento De acordo com a Resolução nº 886/66 do IBGE:
I) < 5 (menor que 5). Quando o primeiro algarismo a ser abandonado é 0,1,2,3 ou 4, ficará inalterado o último algarismo que permanece.
Ex.: 27,14 passa para 27,1 ou 27.
II) > 5 (maior que 5). Quando o primeiro algarismo a ser abandonado é o 6,7,8, ou 9, aumenta-se em uma unidade o algarismo que permanece.
Ex.: 13,87 passa para 13,9 ou 14.
III) = 5 (igual a 5). Quando o primeiro algarismo a ser abandonado é 5, há duas soluções:
A) Se após o 5 seguir, em qualquer casa, um algarismo diferente de zero, aumenta-se uma unidade ao algarismo que permanece.
Ex.: 17,152 passa para 6,2.
B) Se o 5 for o último algarismo ou após o 5 só se seguirem zeros, o último algarismo a ser conservado só será aumentado de uma unidade se for ímpar.
Ex.: 14,75 passa para 14,8
Observação: Nunca devemos fazer arredondamentos de sucessivos.
Para melhor entendimento didático quando o último primeiro algarismo a ser abandonado for 5 o último a permanecer aumenta em uma unidade.
Ex.: 72,5 passa para 73 inteiros.
- O truncamento é a ação de truncar um determinado valor, aplicado principalmente em suas casas decimais. Ele ocorre quando ignoramos os valores de um determinado cálculo que possua uma quantidade maior de casas decimais do que a quantidade determinada para resolução do problema.
É importante então discutir com os alunos a situação apresentada, no caso apresentado foi portanto utilizado o truncamento, por considerar que ao truncar o resultado prático é mais conveniente.
Encerramento

Tempo previsto: 3 minutos.
Orientações: Neste momento é importante destacar o aprendizado e tornar o objetivo da aula consciente e consolidar os conceitos utilizados.
Propósito: Discutir o valor fracionário do resultado da área.
Discuta com a turma:
- Em quais outras situações podem ser utilizados os métodos aprendidos nesta aula?
Atividade de Raio X

Tempo previsto: 10 minutos (slide 32 ao slide 33).
Orientações: Esta atividade visa avaliar a consolidação do que foi aprendido, a atividade deve ser realizada individualmente.Observe quais alunos resolvem utilizando as expressões ou através da contagem dos quadradinhos.
Propósito: Discutir o valor fracionário do resultado da área.
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_22GRM03
Recursos
- Necessários:
- caderno
- lápis
- régua
- grupo de alunos no Whatsapp
- Zoom
- Opcionais:
- Google Sala de Aula
- Meet
- Vídeo: “Propriedades dos quadriláteros”- Khan Academy, disponível em: https://pt.khanacademy.org/math/basic-geo/basic-geometry-shapes/basic-geo-quadrilaterals/v/quadrilateral-properties acesso em 14 de jun 2020.
Para este plano, foque na etapa: Retomada
Aquecimento
Retome os conceitos de quadriláteros, sugerindo a visualização do vídeo “Propriedades dos quadriláteros”, disponível no Khan Academy. Apos a visualização do vídeo peça que respondam as questões:
- Qual a diferença entre as figuras apresentadas?
- Apesar de serem quadriláteros, cada uma delas possui características diferentes:
- Os paralelogramos são quadriláteros que possuem lados paralelos dois a dois, esta característica torna o losango um tipo de paralelogramo, porém o losango obrigatoriamente deve possuir lados iguais, já o paralelogramo não.
- Já o trapézio não possui lados paralelos dois a dois.
Atividade principal
Para a realização da atividade principal os alunos precisam ter acesso ao problema proposto. Para isso, fotografe a atividade principal e disponibilize a imagem no grupo de whatsapp para que os alunos possam pensar sobre ele. Peça que tentem resolver a atividade em três momentos. No primeiro momento, pensando sozinho sobre a situação proposta e anotar todas as suas estratégias de cálculo. No segundo momento, eles deverão pedir a um dos seus familiares que tente resolver a situação problema e compartilhar com o aluno como ele pensou. E para o terceiro momento o aluno e seu familiar devem discutir uma estratégia conjunta ou validar uma feita por eles individualmente. Oriente-os a filmar ou fotografar as suas estratégias e respostas para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
Professor, esse é um dos momentos mais importantes da aula, portanto fique atento às respostas dos alunos. Solicite aos alunos que apresentem suas soluções sobre cada um dos itens. Caso sua aula seja síncrona, você pode explorar esse momento solicitando aos alunos que acionem os microfones e expliquem como chegaram às soluções. Caso contrário, peça que enviem as explicações por mensagens de áudio pelo whatsapp. Outra possibilidade é os alunos fotografarem seus registros para compartilhar no grupo de whatsapp. Faça boas perguntas para mediar as discussões.
Raio X
A atividade do Raio X pode ser usada como tarefa de casa ou como avaliação da aula. Envie e faça a discussão da mesma forma que fez com a atividade principal. Lembre-se também que há atividades complementares que podem ser enviadas para os alunos como atividades de fixação ou sistematização.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alex de Cassio Macedo
Mentora: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF07MA26) Resolver e elaborar problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas.
Objetivos específicos
Calcular as medidas de superfície a partir da decomposição em triângulos e quadriláteros.
Conceito-chave
Calcular área por meio de decomposição.
Recursos necessários
- Atividades impressas em folhas.
- Régua, lápis, borracha, caderno.
- Giz ou fita crepe.