Resolução da atividade principal
Plano de Aula
Plano de aula: Recortando e colando retalhos: cálculo de áreas por decomposição
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Medição de superfícies
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alex de Cassio Macedo
Mentora: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF07MA25) Estabelecer expressões de cálculo de área de triângulos e de quadriláteros.
Objetivos específicos
Analisar a importância das decomposições de figuras planas no cálculo de medidas de superfície (área).
Conceito-chave
Obtenção de expressões para o cálculo de áreas
Recursos necessários
- Folha de papel quadriculado (impressão disponível aqui);
- Atividades impressas em folhas.
- Tesoura, régua, lápis, borracha, caderno.
- Dependendo da preferência do professor pode ser usado retalhos de tecido.
Título do plano - Planos de aula - 7º ano
Habilidades BNCC:
Objetivos de aprendizagem
Analisar a importância das decomposições de figuras planas no cálculo de medidas de superfície (área).
Resumo da aula
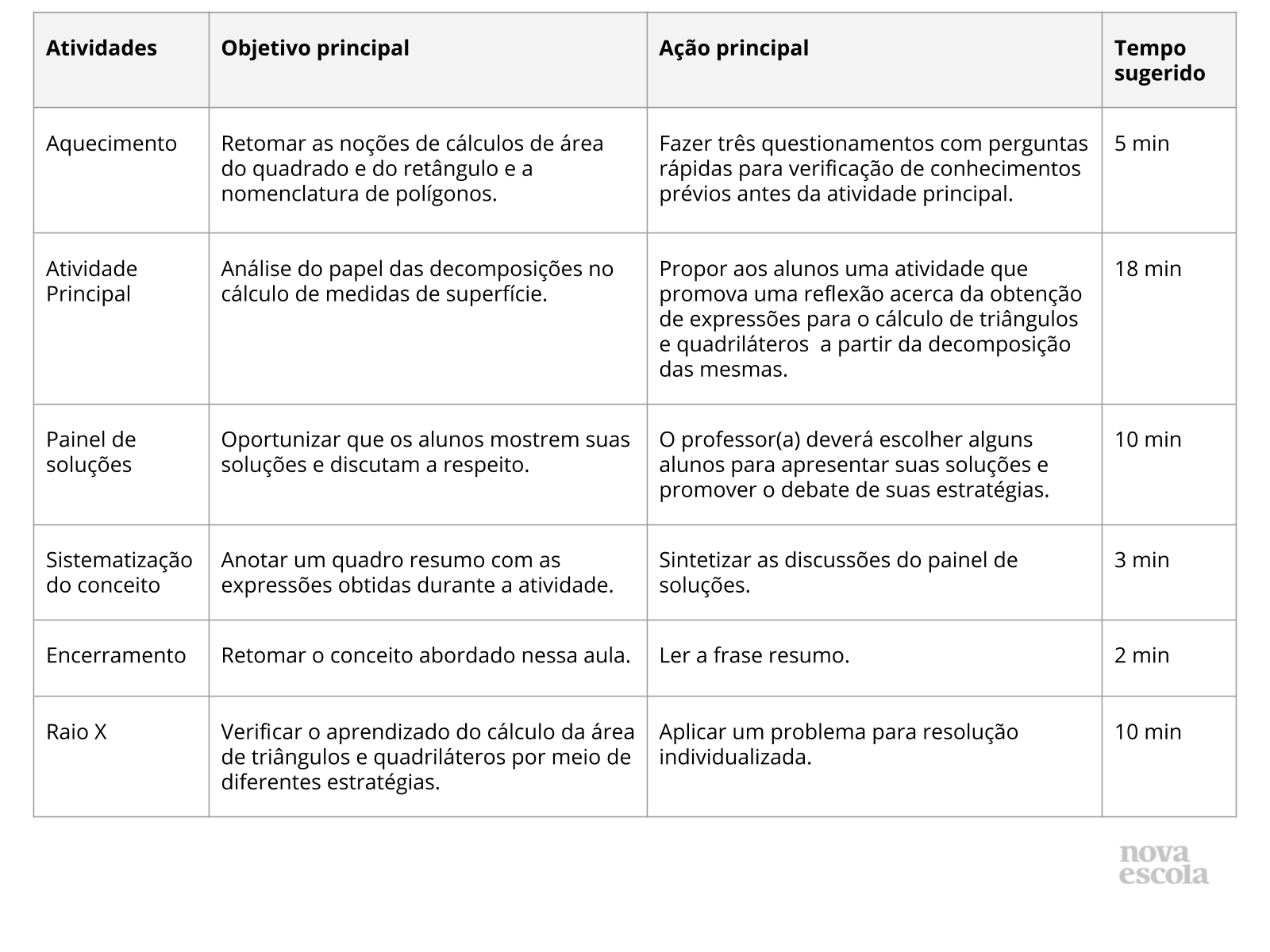
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo da aula

Tempo sugerido: 2 minutos.
Orientação: Neste primeiro momento explique o objetivo da aula de maneira clara e sucinta, argumente que a partir desta aula o aluno(a) será capaz de calcular medidas de superfície ou áreas em diversas situações, decompondo - as em figuras mais simples e conhecidas.
Propósito: Compartilhar o objetivo da aula e motivá-los ao estudo.
Aquecimento

Tempo previsto: 5 minutos.
Orientações: Neste momento, é importante retomar os conceitos de área do quadrado e do retângulo, cuide para não revelar a resolução préviamente do problema proposto.
Propósito: Promover uma retomada de conceitos relacionados ao cálculo da área de quadrados .
Discuta com a turma:
- Qual a diferença de quadrado e retângulo.
- Como se calcula a área de um quadrado.
- O que ocorre com a área de uma quadrado se a medida do seu lado aumentar.
Aquecimento (Continuação)
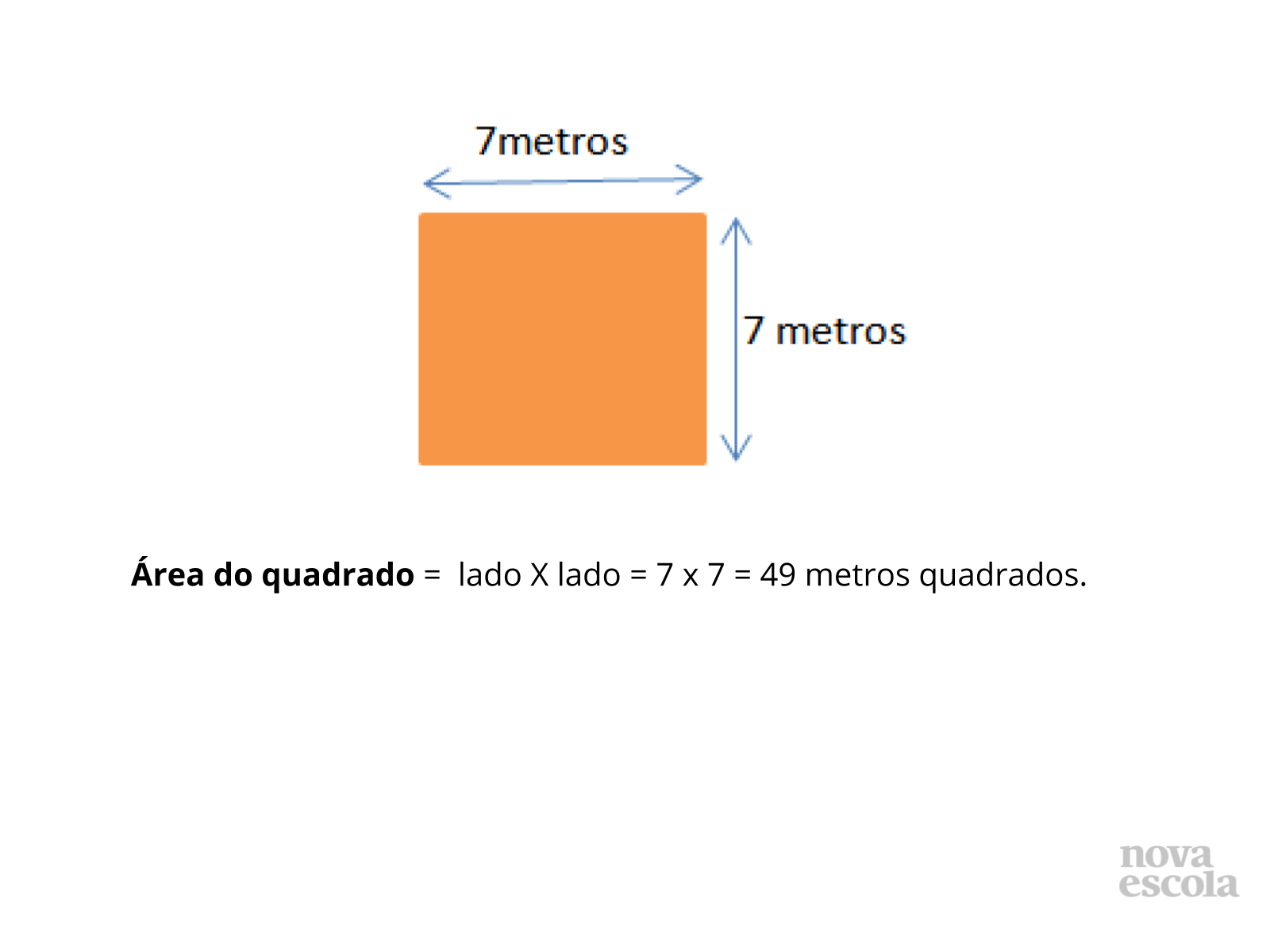
Orientações: Mostre esta resolução e comente como ela pode ser expressa de maneira mais genérica também , por meio da expressão ÁREA DO QUADRADO = LADO X LADO OU ÁREA DO QUADRADO = (LADO)².
Propósito: Promover uma retomada de conceitos relacionados ao cálculo da área de quadrados .
Aquecimento (Continuação)

Orientações: Neste momento, é importante retomar os conceitos de área do retângulo. Cuide para não revelar a resolução préviamente do problema proposto.
Propósito: Promover uma retomada de conceitos relacionados ao cálculo da área de retângulos .
Discuta com a turma:
- Como utilizar corretamente os termos: comprimento, largura e altura conforme a situação em um retângulo.
Aquecimento (Continuação)
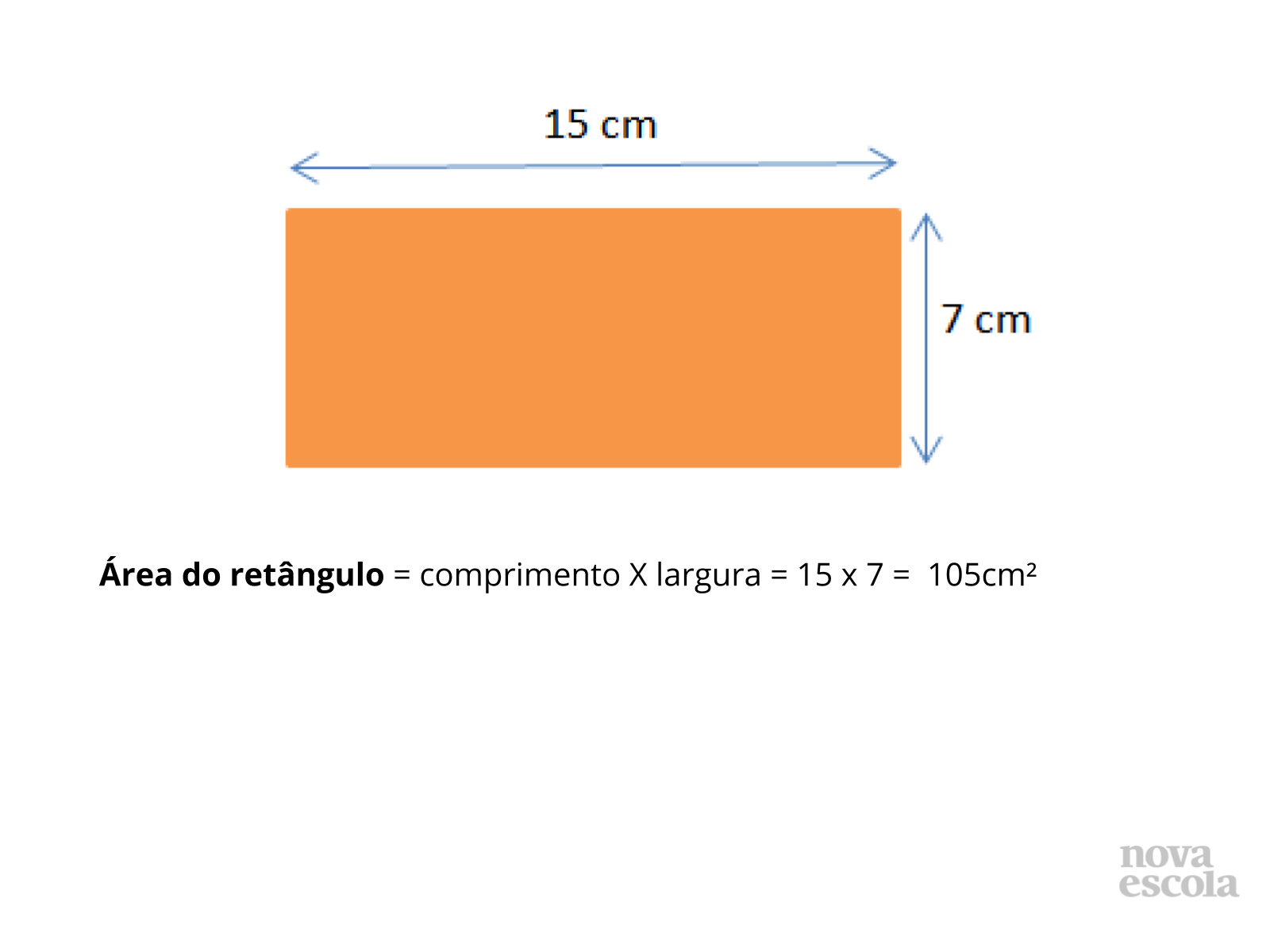
Orientações: Mostre esta resolução e comente como ela pode ser expressa de maneira mais genérica também , por meio da expressão ÁREA D O RETÂNGULO = COMPRIMENTO X LARGURA.
Propósito: Promover uma retomada de conceitos relacionados ao cálculo da área de retângulos .
Aquecimento ( Continuação)
Orientações: Esta pergunta deve ser respondida oralmente. Professor, para orientar melhor seus alunos sobre a nomenclatura dos Polígonos clique aqui.
Propósito: Retomar a nomenclatura dos polígonos.
Discuta com a turma:
- O que é um quadrilátero?
- Todas as figuras são quadriláteros.
Aquecimento (continuação)
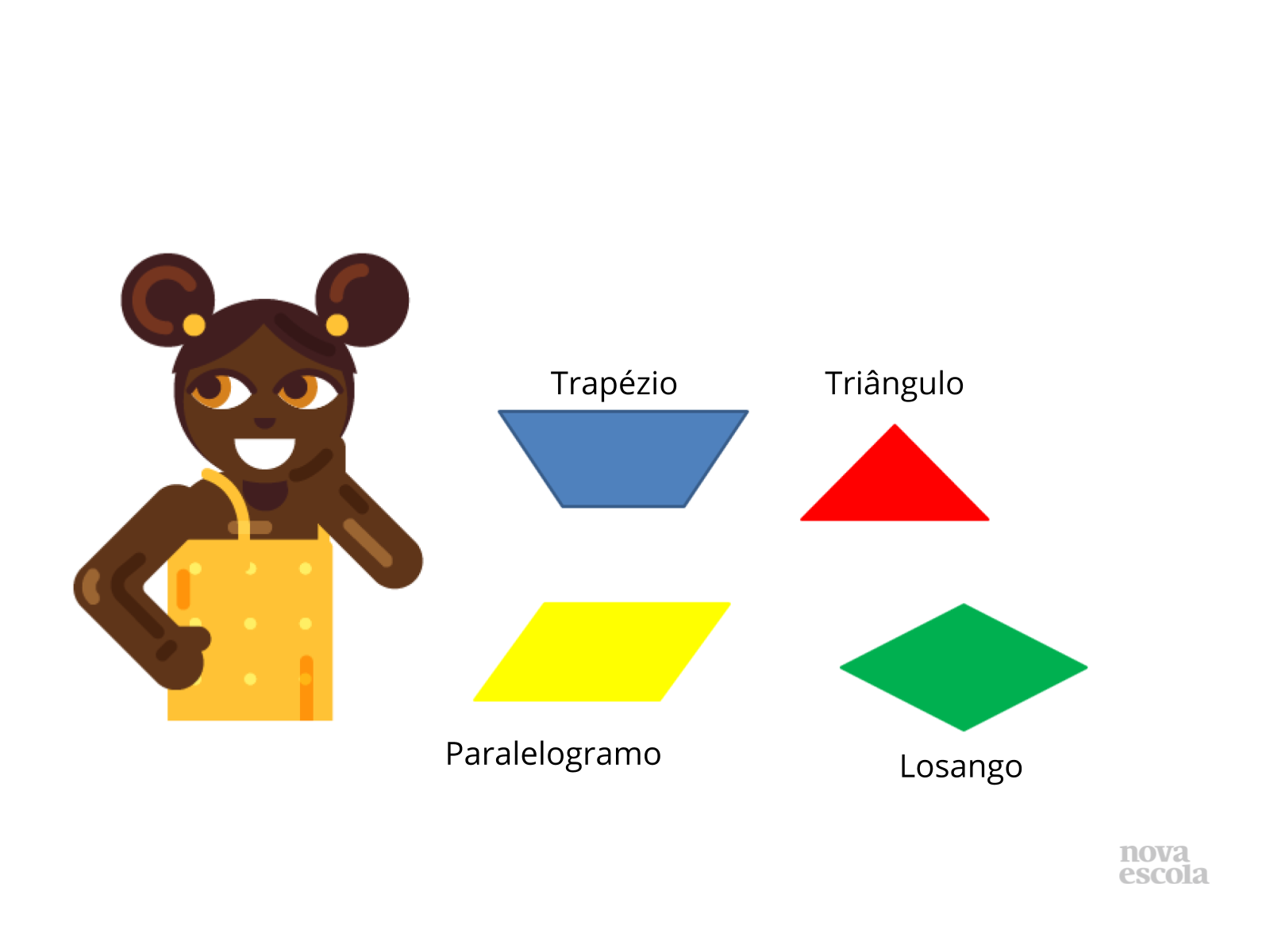
Propósito: Retomar a nomenclatura dos polígonos.
Discuta com a turma:
- O que é um quadrilátero?
- Todas as figuras são quadriláteros.
Atividade Principal
Tempo sugerido: Total 18 minutos (9 minutos na primeira parte + 9 minutos na segunda parte).
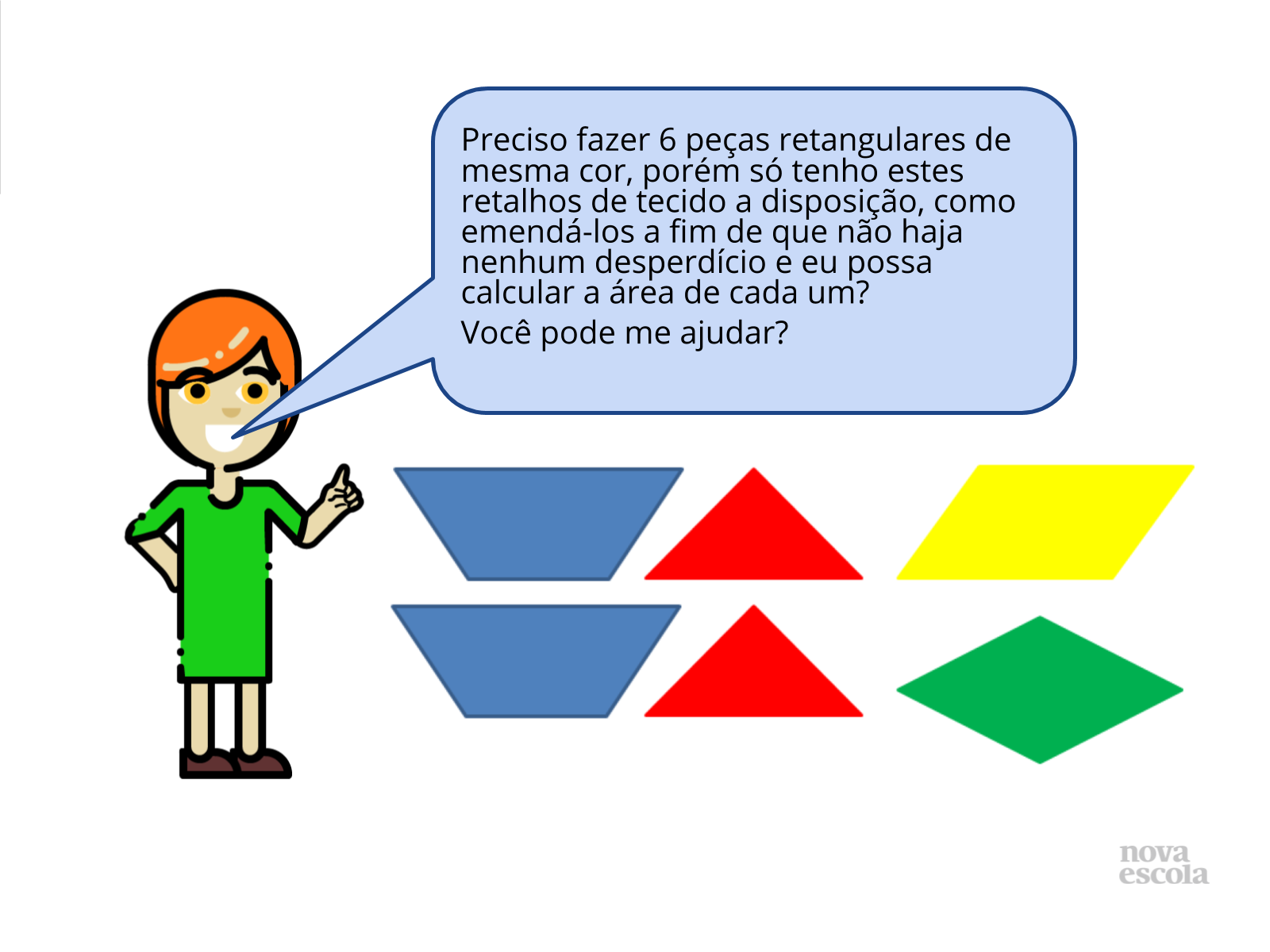
Orientações: Leia com os alunos a atividade e certifique-se de que todos compreenderam o problema. Nesta atividade é importante que você deixe-os livre para planejar criativamente uma maneira de resolver o problema proposto. Deixe claro que a partir dos “retalhos” (papéis) fornecidos deseja-se que se faça 6 retângulos de mesma cor, ou seja, não se deve montar um retângulo com duas ou mais cores.
O modelo com os retalhos devem ser impressos (Aqui!) e recortados antecipadamente. Uma boa opção também seria o professor providenciar retalhos de tecidos ou pedir que os alunos tragam retalhos de tecido para a aula, porém é importante que tenham o tamanho e formato dos modelos.
A resolução desta atividade pode ser acessada Aqui!
Propósito: Fazer com que os alunos compreendam e se familiarize com o problema.
Discuta com a turma:
- Quem iniciou a divisão, distribuindo primeiro as fichas 1? O que aconteceu?
- Por que é mais prático iniciar a divisão pela ficha de maior valor?
- Se sobrar uma ficha de valor 100, a atividade se encerra? Por quê?
Atividade Principal (Primeira parte)
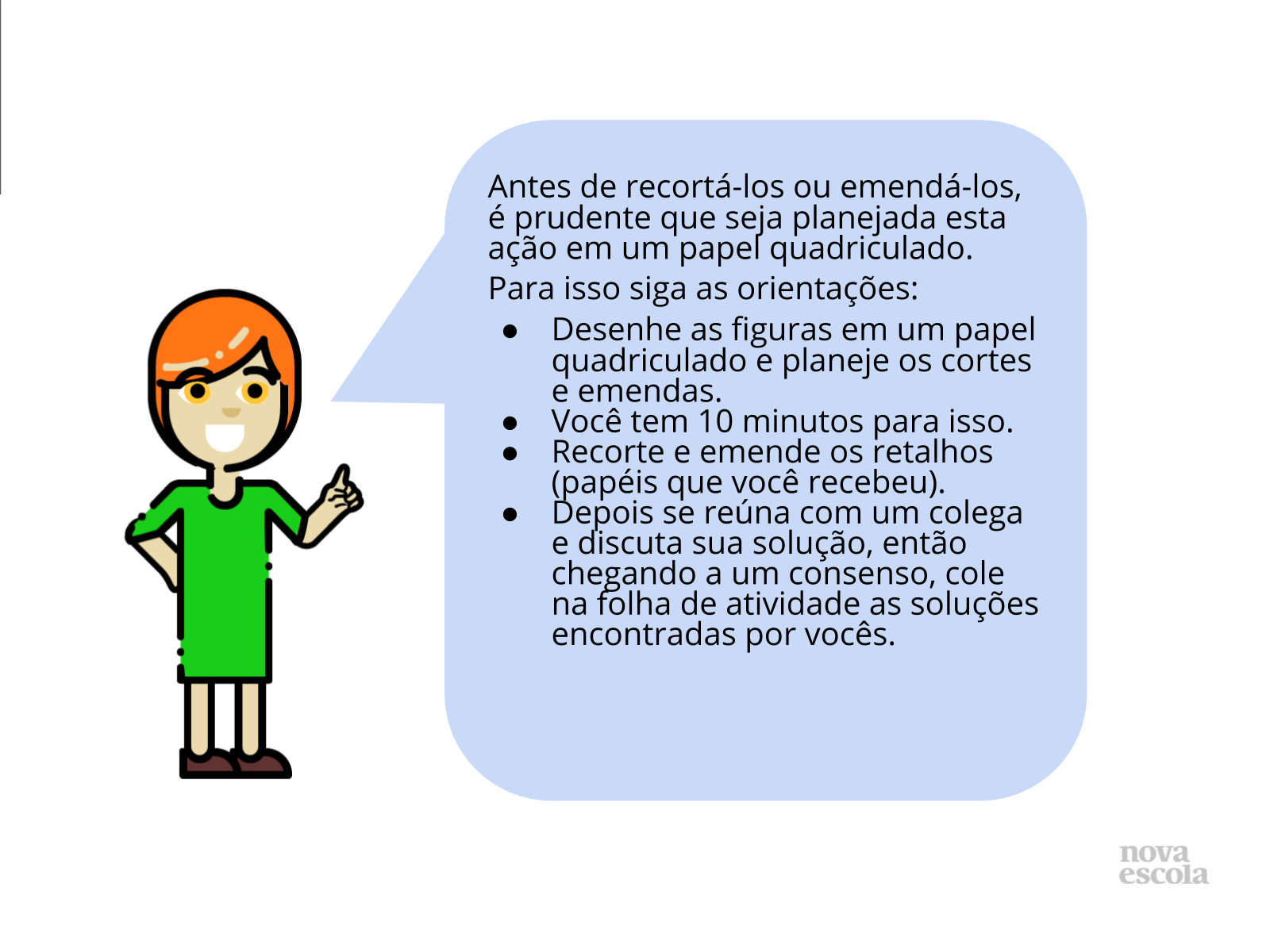
Tempo sugerido: 10 minutos.
Orientações: Nesta primeira parte da atividade, antes dos alunos realizarem os cortes e emendas devem racionalizar primeiro a ação utilizando o desenho dos retalhos em uma folha com quadrículas, esta parte deve ser individual de maneira que cada um possa criar suas conjecturas sobre a solução do problema. Distribua a folha da atividade (primeira parte) e oriente-os a desenhar as transformações das figuras na folha quadriculada. Faça o download da atividade
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Utilize o guia de intervenções para discutir com os alunos as possibilidades de recorte e emenda das figuras. Você encontra o Guia de Intervenções na aba Materais complementares desse plano.
Propósito: Fazer com que os alunos pensem a ação e proponham soluções.
Discuta com a turma:
- A figura obtida é realmente um retângulo?
- A quantidade de quadrículas se mantém no retalho e no retângulo emendado?
Atividade Principal (Segunda parte)

Tempo sugerido: 10 minutos.
Orientações: A segunda parte da atividade deve ser realizada em dupla. Oriente aos alunos que esta é a hora de discutir a soluções encontradas na primeira parte e verificar se há consenso e se as soluções foram obtidas mesmo que por estratégias distintas. Peça que agora recortem e montem o retângulo a partir do retalho (papel ou pano) na folha da segunda parte da atividade. Nela, os alunos devem comparar o retângulo e o formato original do retalho, chame a atenção para o fato de que as duas figuras possuem a mesma área e que ao calcular a área do retângulo estamos encontrando também a medida da área do retalho original. Peça lhes que comparem o nome das dimensões nas duas figuras (retângulo e retalho) e busquem encontrar uma expressão para o cálculo da área do retalho (relembre-os do que foi discutido no aquecimento! ).
Utilize o guia de intervenções para abordagem de possíveis dificuldades.
Propósito: Fazer com que os alunos reflitam sobre a decomposição dos retalhos e a equivalência das áreas obtidos como um importante recurso para a obtenção de uma expressão para o cálculo das medidas de suas áreas.
Discuta com a turma:
- O que significam as dimensões? Como são chamadas em cada figura?
- Por que é importante se conhecer uma expressão para a medida de áreas?
Discussão das soluções

Tempo sugerido: 10 minutos (slides 13 a 16).
Orientações: Depois que os alunos compartilharem as estratégias deles, passe para esta série de slides. Nela, os alunos verão, passo a passo, e poderão discutir suas soluções e estratégias, deixe que eles mesmos avaliem seu percurso de maneira que se algo está errado ele mesmo perceba através da discussão dos colegas. Caso, seja necessário convide uma ou duas duplas para apresentarem sua solução antes de seguir com os demais slides (isso pode embasar as respostas aos slides e até mesmo gerar comparações).
Propósito: Realizar uma apresentação das estratégias de resolução, visando a auto correção e a síntese da atividade.
Discussão das soluções
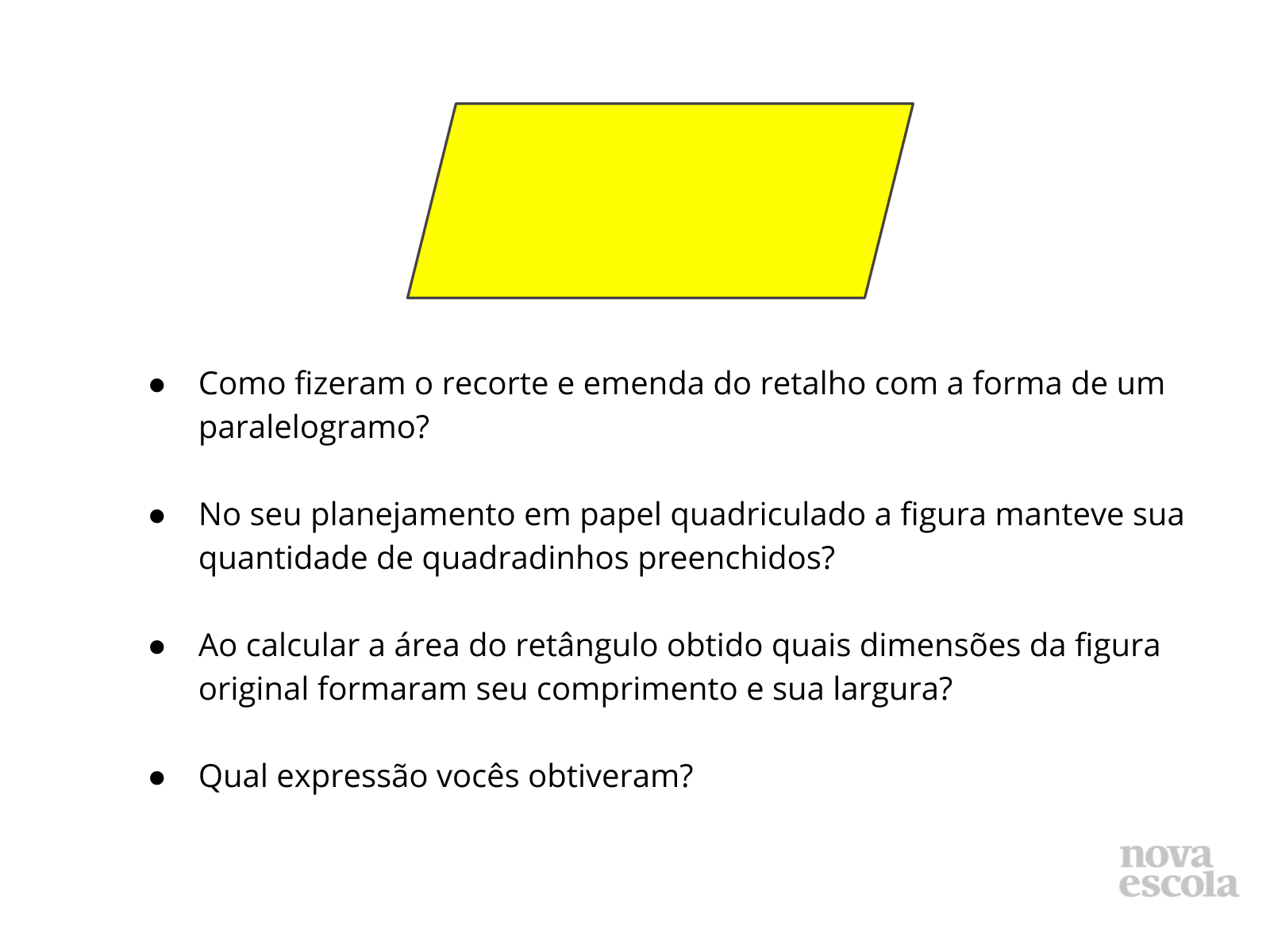
Orientações: Leia com os alunos as perguntas e verifique as respostas, dê atenção e discuta mais caso ocorram respostas diferentes das esperadas.
Discussão das soluções
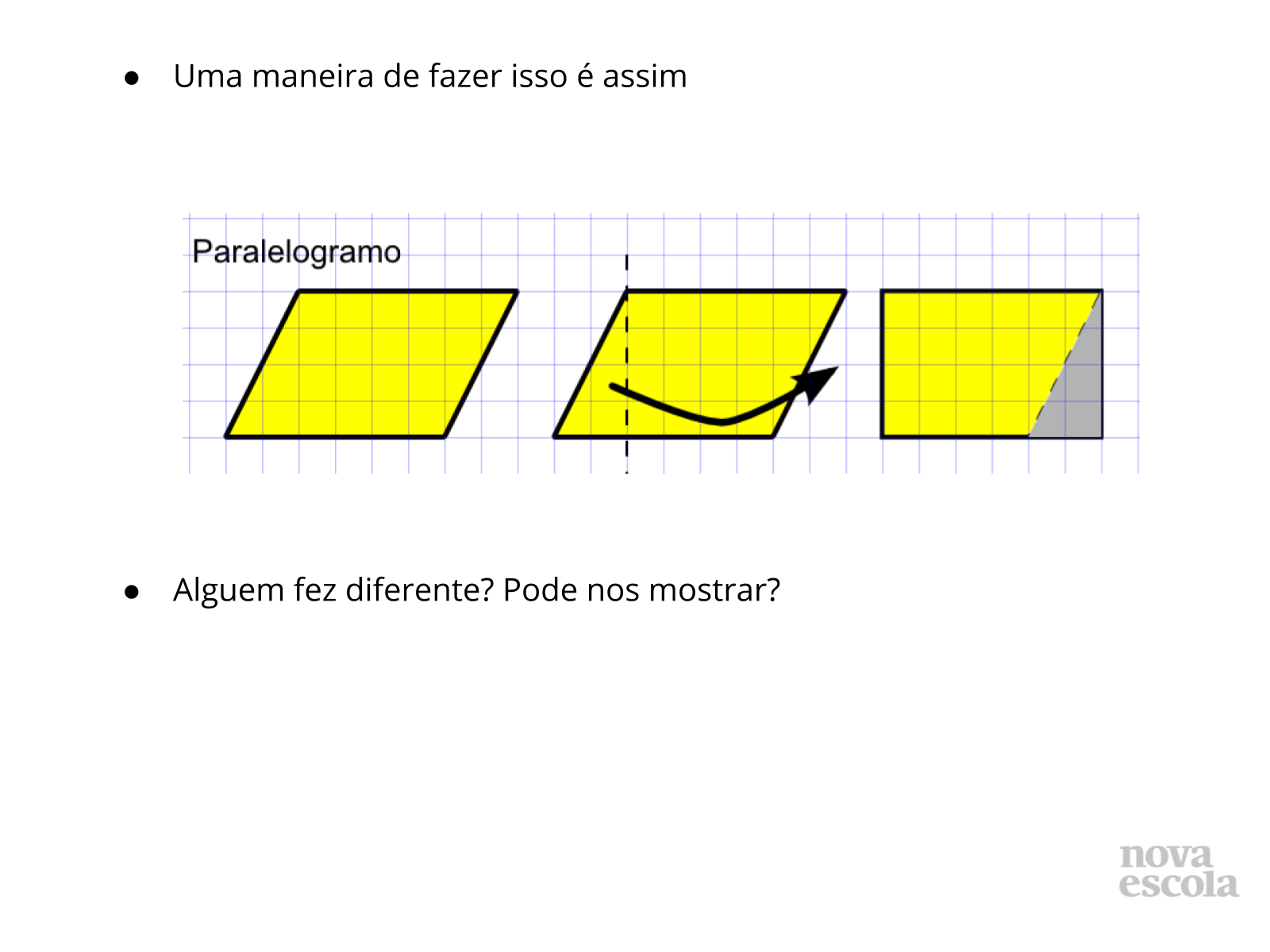
Orientações: Espera-se que a maioria dos alunos realize desta maneira a atividade porém, valorize outras maneiras de resolução, mesmo que erradas, se oriente pelas perguntas anteriores e verifique junto aos alunos porque a solução encontrada não é adequada.
Discussão das soluções
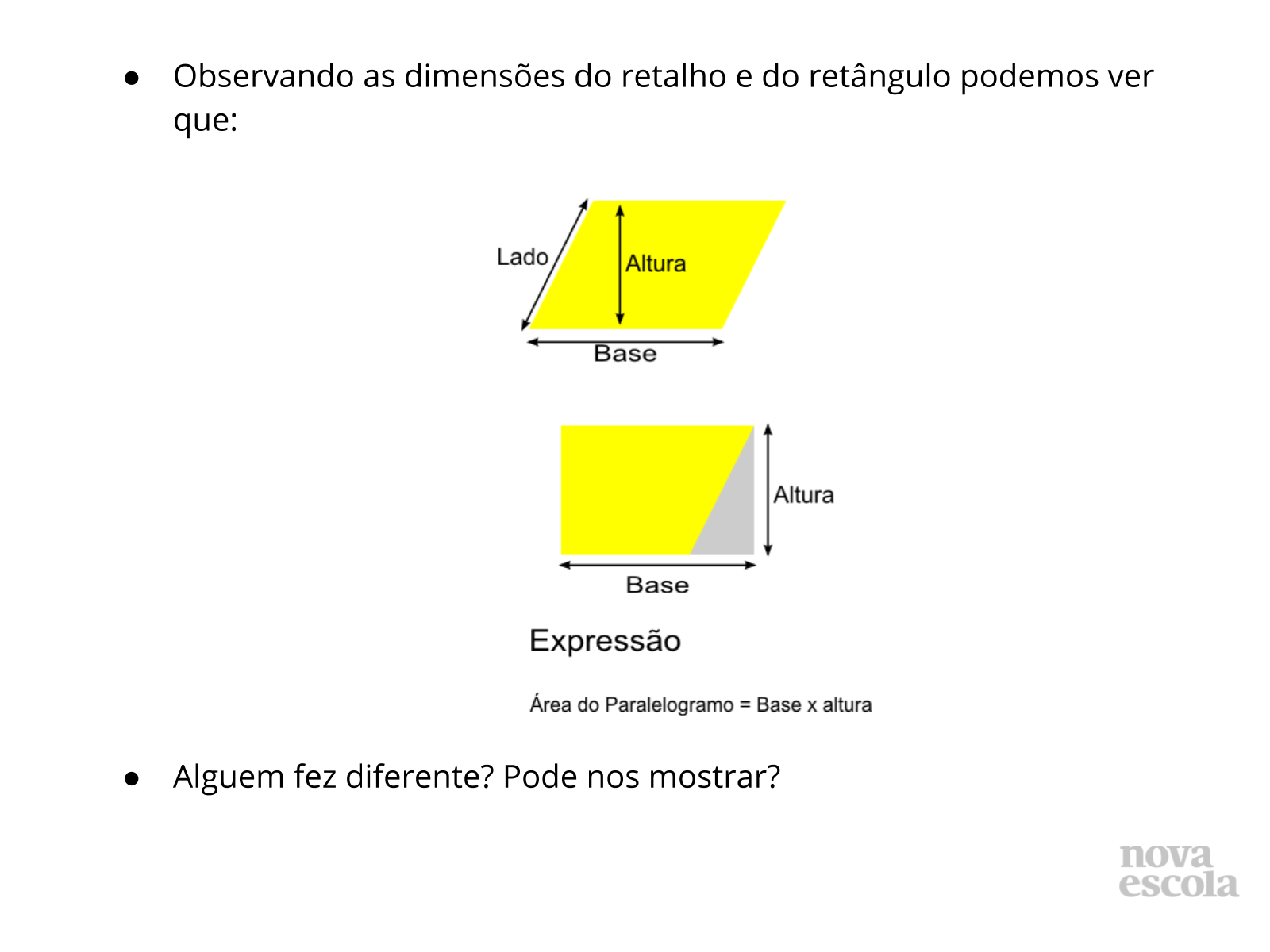
Orientações: Chame a atenção dos alunos para as dimensões antes e depois da criação do retalho, comparando as medidas, pensando na área do retângulo eles conseguiram “enxergar” a expressão para o cálculo da área do paralelogramo.
Discussão das soluções
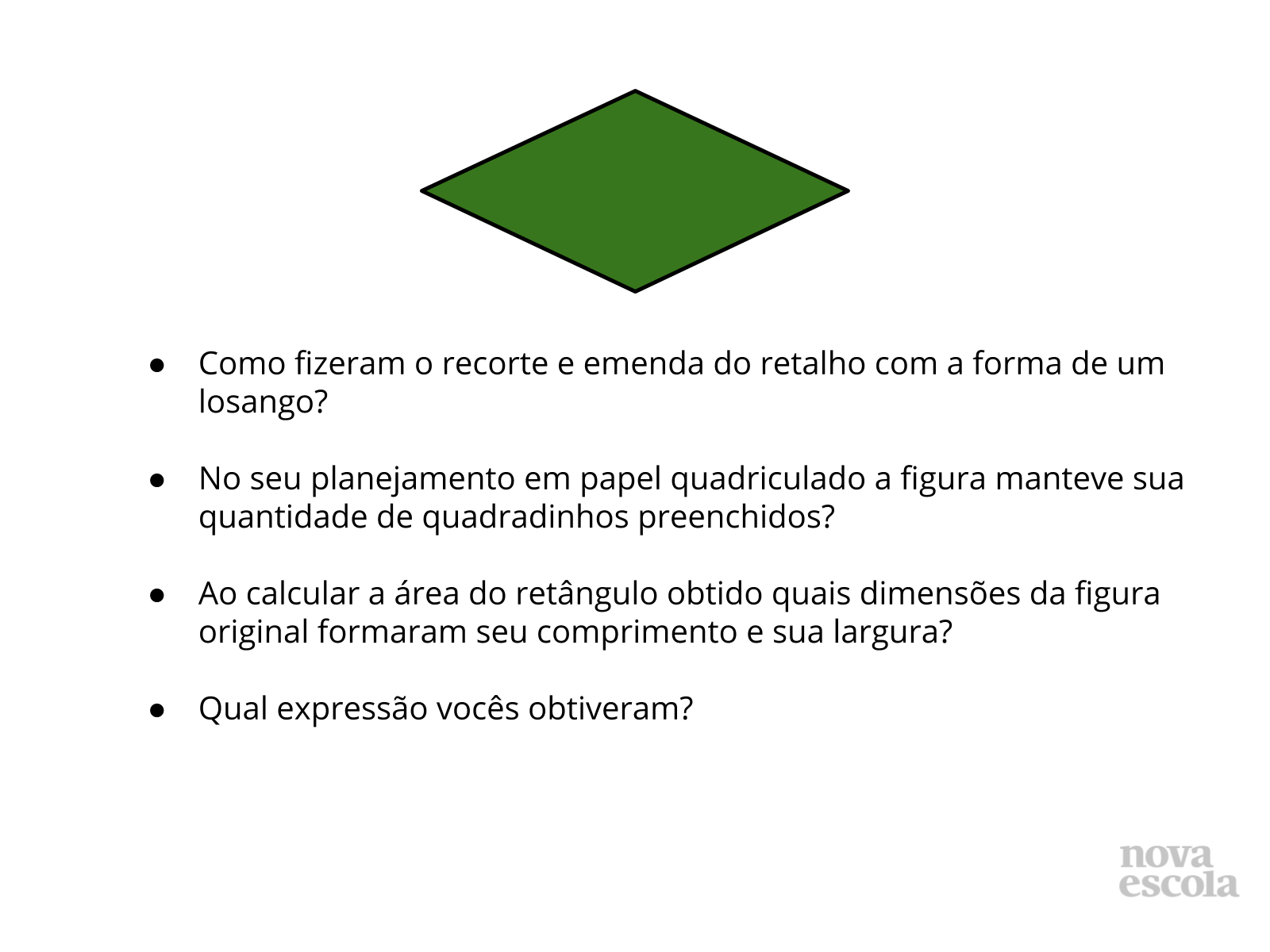
Orientações: Leia com os alunos as perguntas e verifique as respostas, dê atenção e discuta mais caso ocorram respostas diferentes das esperadas.
Discussão das soluções
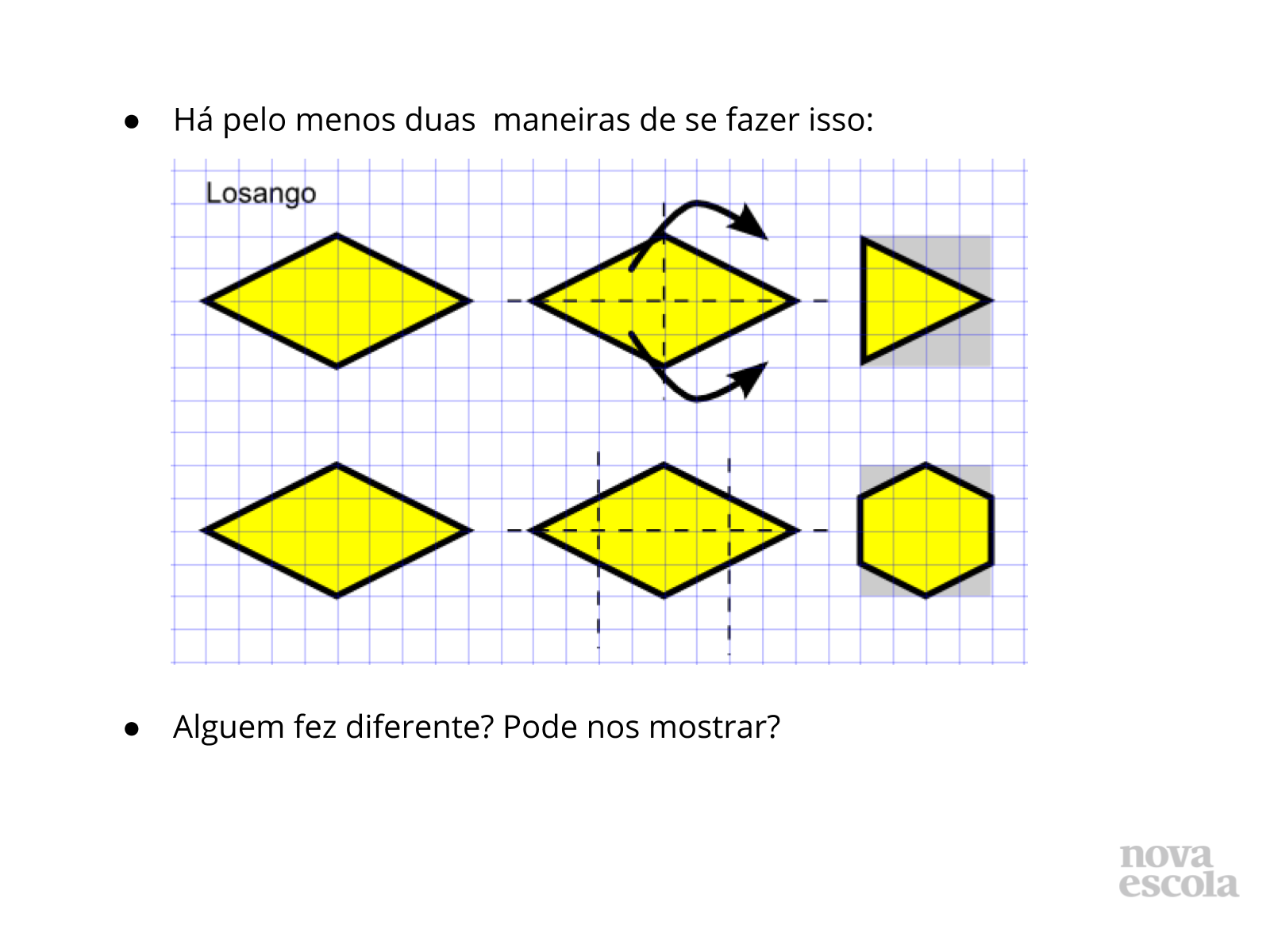
Orientações: Espera-se que a maioria dos alunos realize desta maneira a atividade porém valorize outras maneiras de resolução, mesmo que erradas, se oriente pelas perguntas anteriores e verifique junto aos alunos porque a solução encontrada não é adequada.
Discussão das soluções
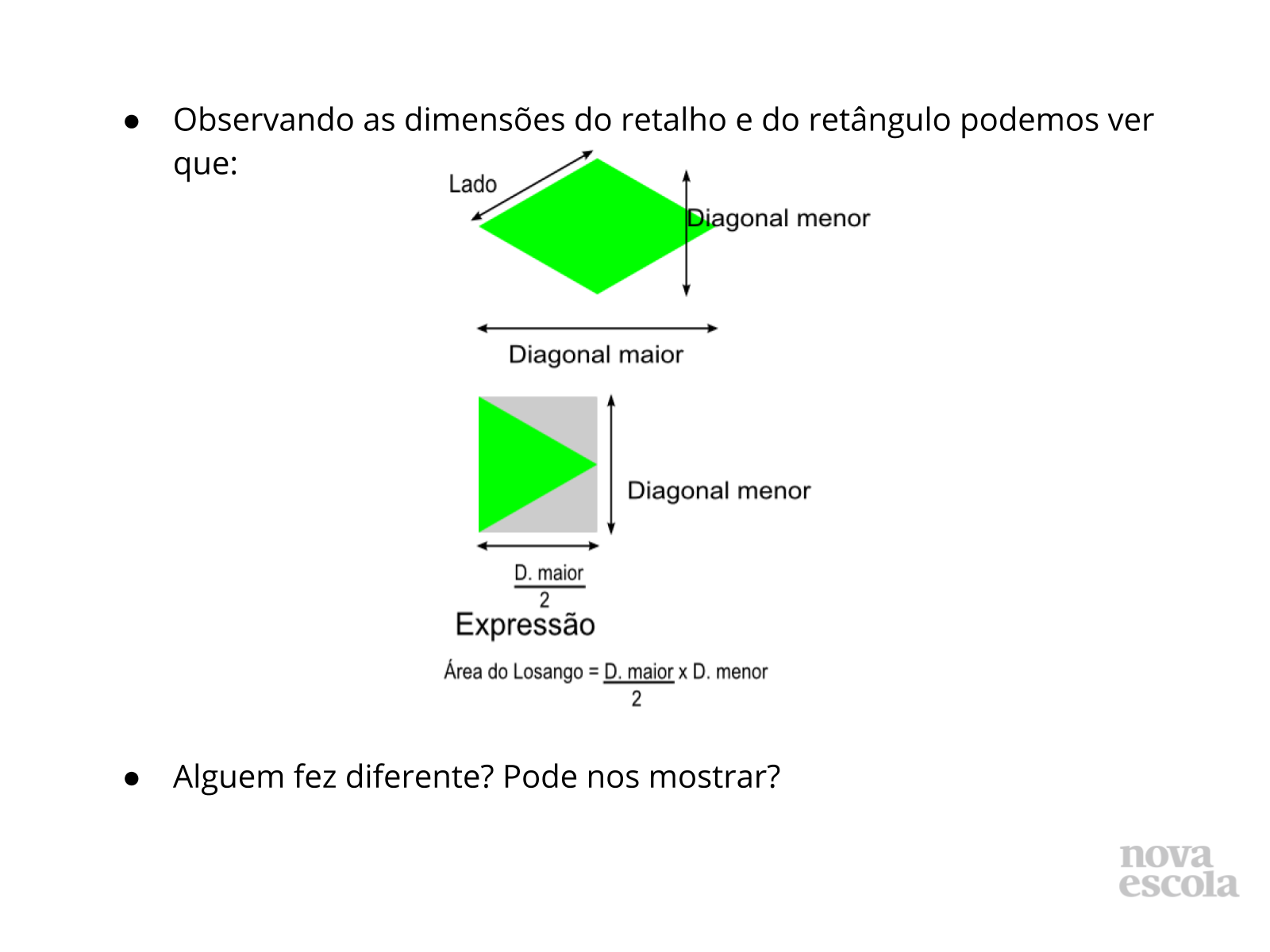
Orientações: Chame a atenção dos alunos para as dimensões antes e depois da criação do retalho, comparando as medidas e pensando na área do retângulo eles conseguiram “enxergar” a expressão para o cálculo da área do losango. Destaque a necessidade de se dividir uma das bases para a obtenção do retângulo.
Discussão das soluções
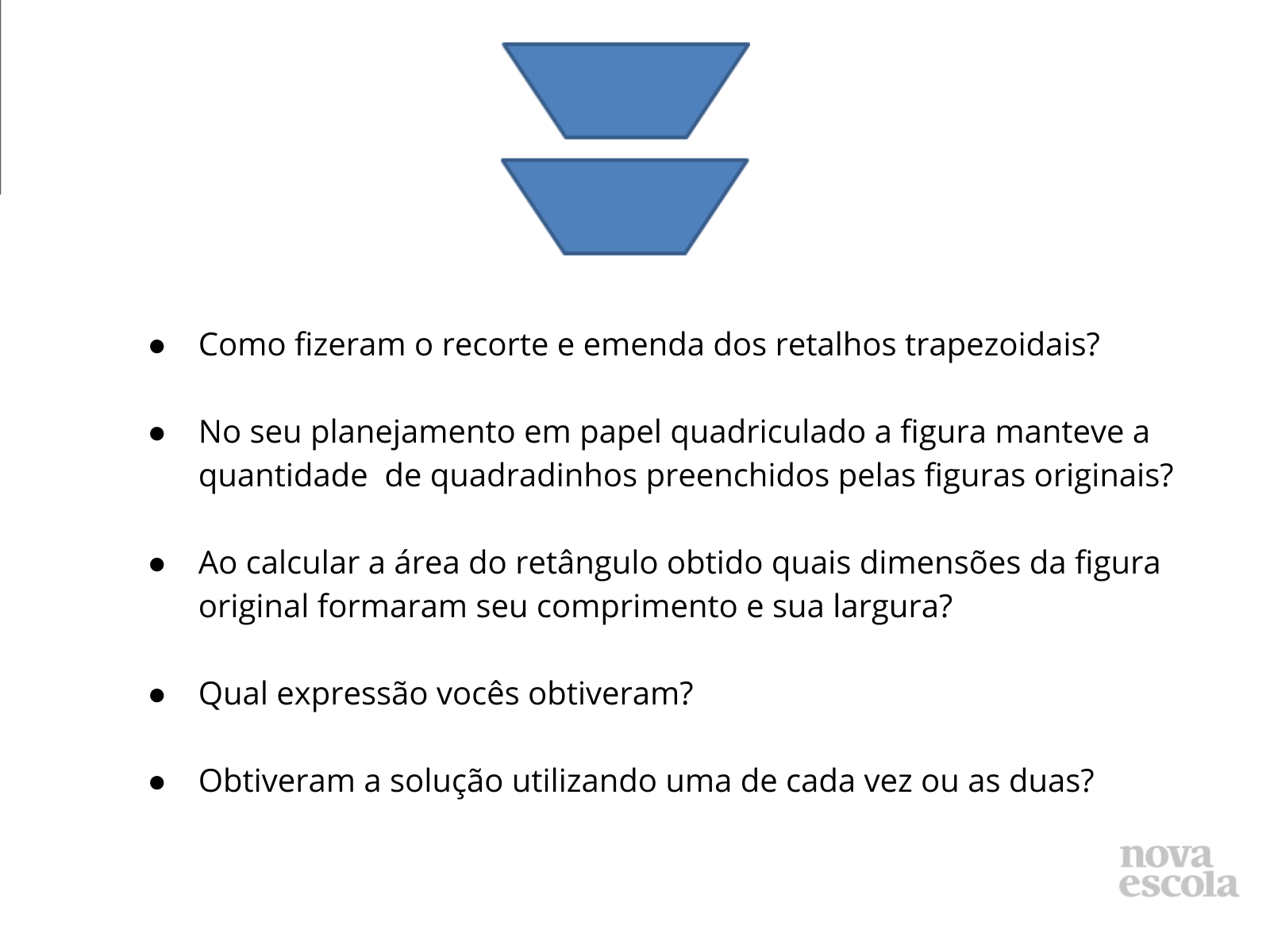
Orientações: Espera-se que a maioria dos alunos realize desta maneira a atividade porém, valorize outras maneiras de resolução, mesmo que erradas, se oriente pelas perguntas anteriores e verifique junto aos alunos porque a solução encontrada não é adequada.
Discussão das soluções
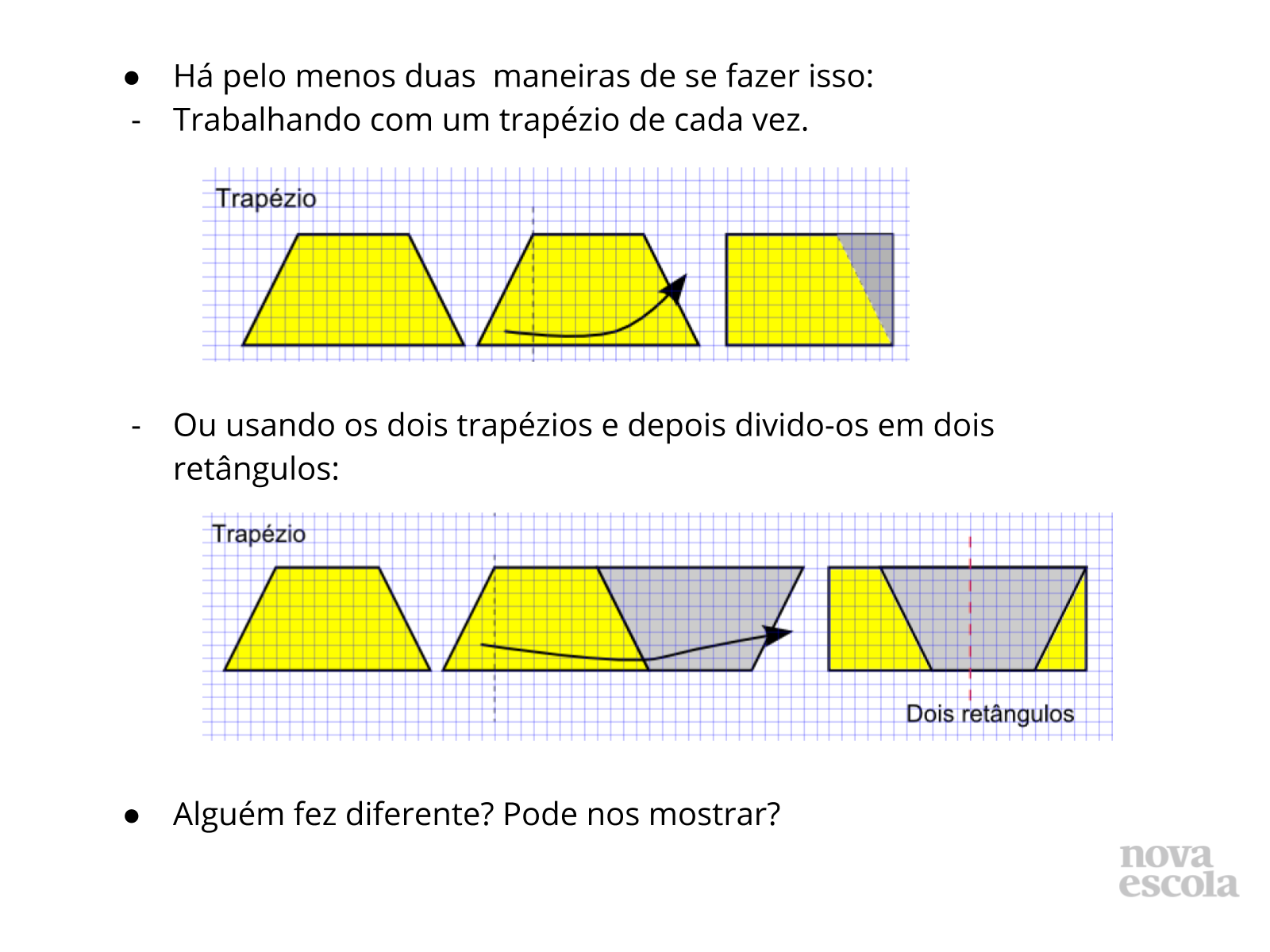
Orientações: Espera-se que a maioria dos alunos realize desta maneira a atividade porém, valorize outras maneiras de resolução, mesmo que erradas, se oriente pelas perguntas anteriores e verifique junto aos alunos porque a solução encontrada não é adequada.
Discussão das soluções
Orientações: Chame a atenção dos alunos para as dimensões antes e depois da criação do retalho, comparando as medidas e pensando na área do retângulo eles conseguiram “enxergar” a expressão para o cálculo da área do losango. Destaque a necessidade de se dividir uma das bases para a obtenção do retângulo.
Discussão das soluções
Orientações: Espera-se que a maioria dos alunos realize desta maneira a atividade porém, valorize outras maneiras de resolução, mesmo que erradas, se oriente pelas perguntas anteriores e verifique junto aos alunos porque a solução encontrada não é adequada.
Discussão das soluções
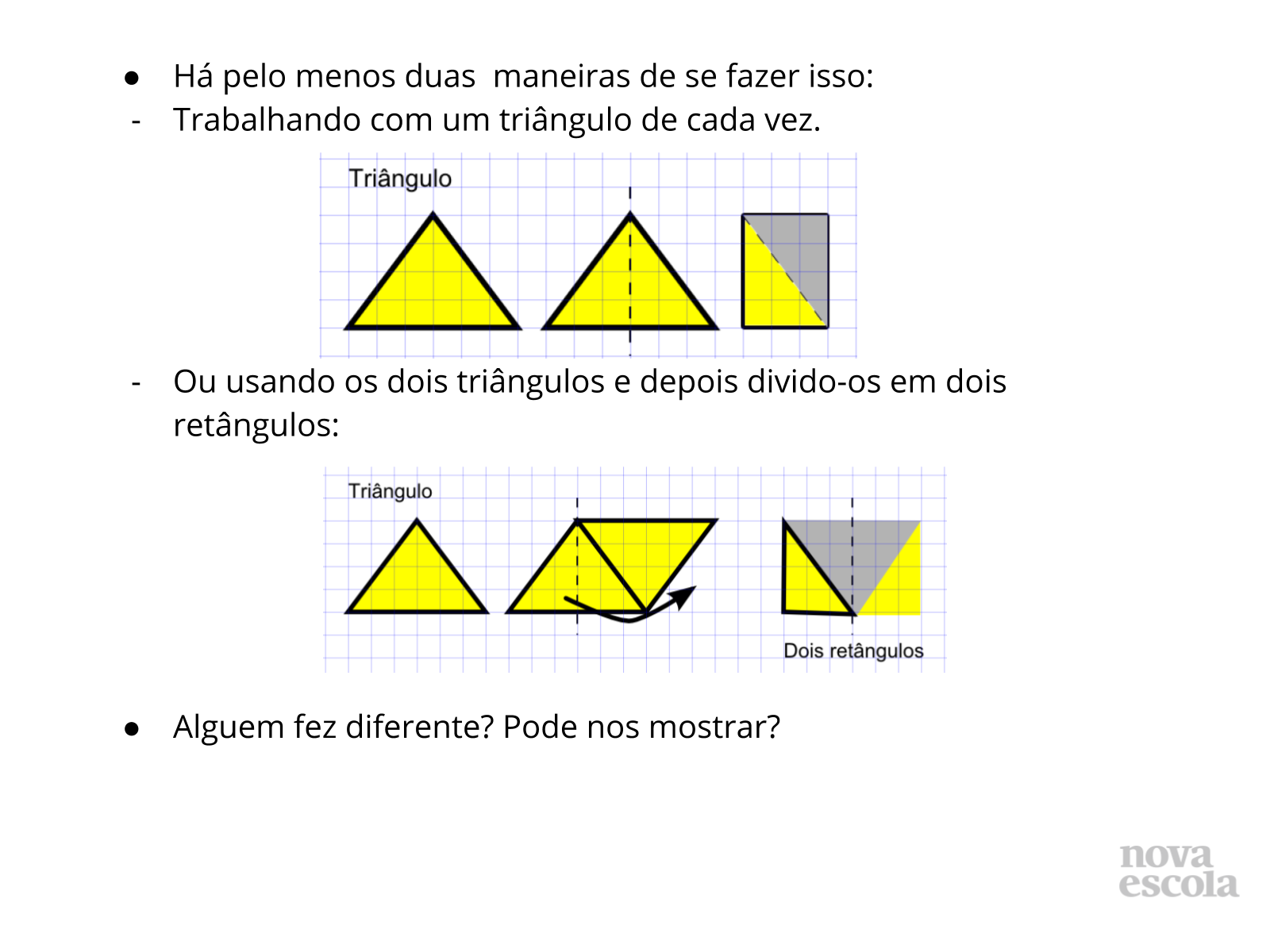
Orientações: Espera-se que a maioria dos alunos realize desta maneira a atividade porém, valorize outras maneiras de resolução, mesmo que erradas, se oriente pelas perguntas anteriores e verifique junto aos alunos porque a solução encontrada não é adequada.
Discussão das soluções
Orientações: Chame a atenção dos alunos para as dimensões antes e depois da criação do retalho, comparando as medidas e pensando na área do retângulo eles conseguiram “enxergar” a expressão para o cálculo da área do losango. Destaque a necessidade de se dividir uma das bases para a obtenção do retângulo.
Sistematização do conceito

Tempo sugerido: 5 minutos.
Orientações: Encerre a atividade retomando as discussões e montando um quadro com as expressões obtidas, espera-se que este quadro contenha
Paralelogramo -> área do paralelogramo = comprimento x altura.
Losango - > área do losango = Diagonal maior x diagonal menor.
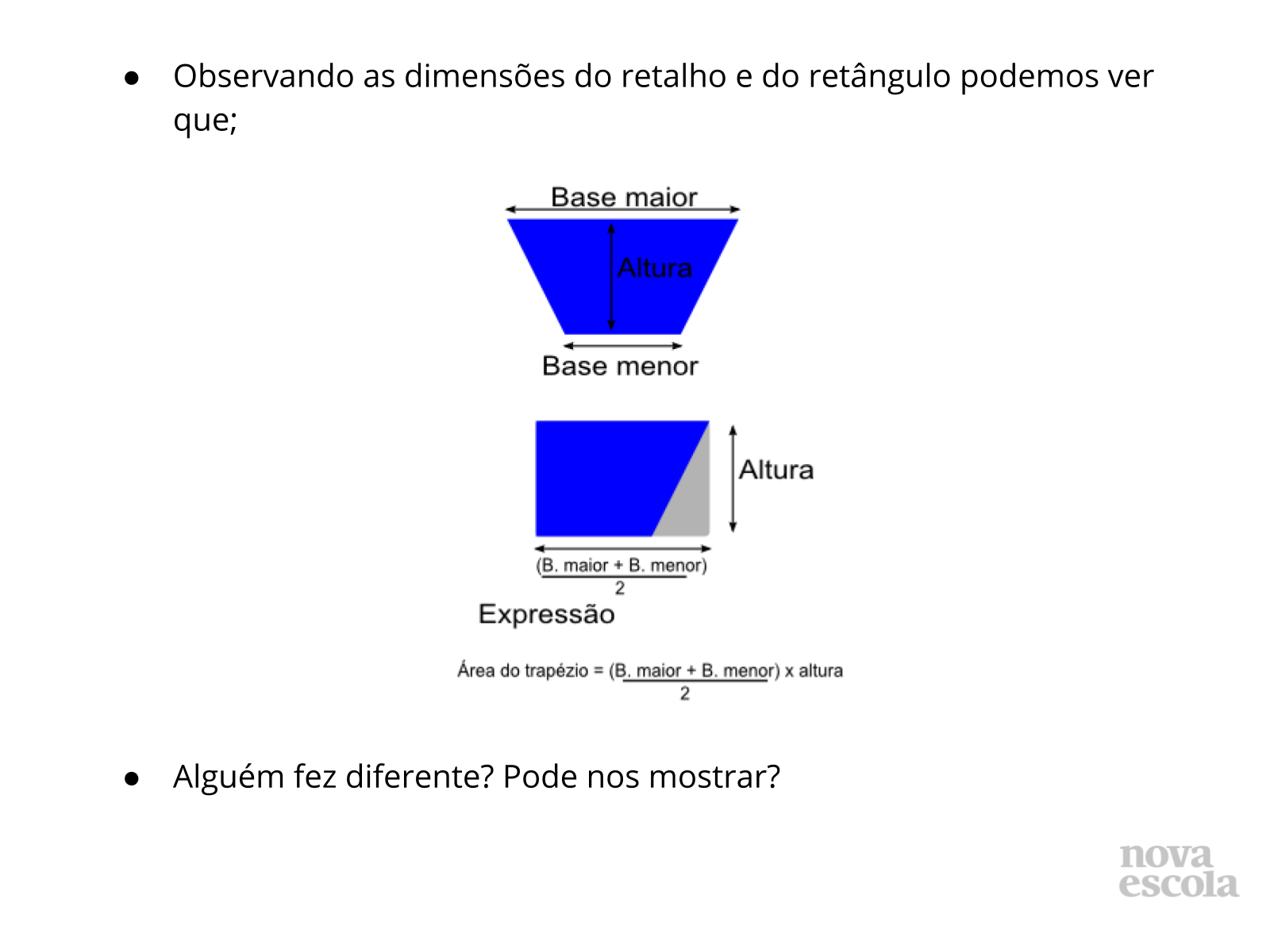
Trapézio -> área do trapézio =
(Base maior + base menor) x altura
2
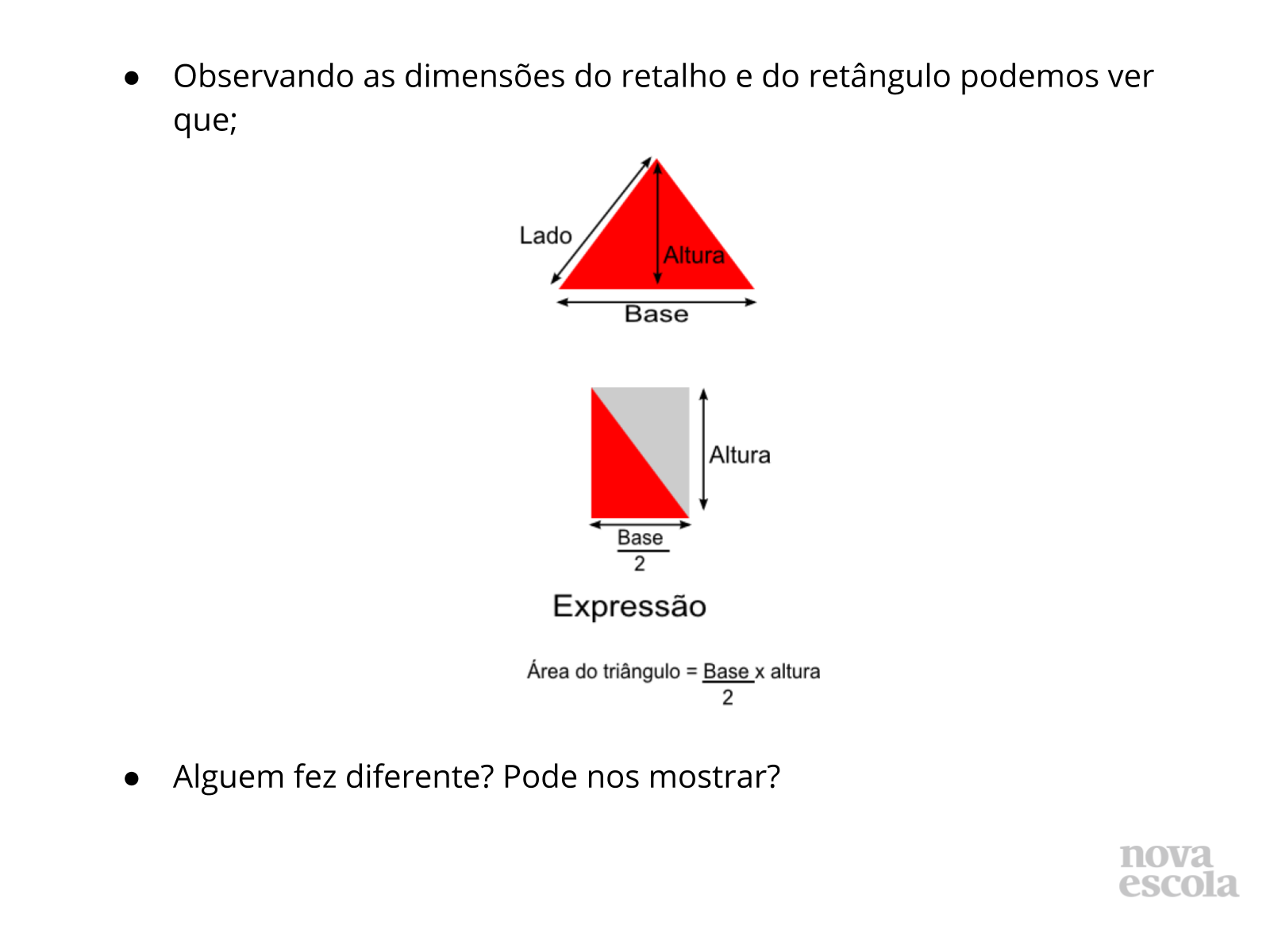
Triângulo -> área do triângulo = Base x altura
2
Pode-se ainda incluir neste quadro o retângulo e o quadrado.
Encerramento

Tempo sugerido: 3 minutos.
Orientações: Professor, leia para os alunos o resumo dessa aula.
Propósito: Retomar os conceitos trabalhados.
Atividade Raio X (Introdução)

Tempo sugerido: 10 minutos.
Atividade Raio X

Tempo sugerido: 10 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e resolvam. Nesta atividade o aluno pode desenvolver sua resolução de acordo com a estratégia que achar melhor, seja por expressão seja pela decomposição de figuras com o auxílio da malha. Assim, o professor pode avaliar que tipo de apropriação cada aluno teve do assunto abordado.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos e avaliar os conhecimentos de cada um a respeito do cálculo de áreas a partir da decomposição ou das expressões obtidas durante a aula.
Resolução Atividade Raio X: Clique aqui,
Sugestão de adaptação para ensino remoto
Código do plano
MAT7_22GRM02
Recursos
- Necessários:
- caderno
- lápis
- régua
- grupo de alunos no Whatsapp
- Opcionais:
- Google Sala de Aula
- Meet
- Vídeo: “Área e Perímetro”- Khan Academy, disponível em: https://www.youtube.com/watch?v=QGLnIyop0P4 acesso em 04 de jul 2020.
Para este plano, foque na etapa: Atividade Principal
Aquecimento
Sugira a visualização do vídeo “Área e Perímetro” disponível no Khan Academy para a retomada dos conceitos.
Atividade principal
Disponibilize a atividade pelo meio de comunicação estabelecido com a turma, sugira que os alunos recortem retalhos de tecidos para realizar a atividade. Oriente-os que é um momento de retomada de conteúdos e que caso tenham dúvidas, estas serão trabalhadas no decorrer da aula.
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Os alunos devem postar seus vídeos ou fotografias para compartilhar suas respostas em um ambiente de interação como WhatsApp ou Google Sala de Aula, por exemplo. A intenção é formar um painel de soluções e promover uma discussão rica e estimuladora entre os alunos e professor.
Raio X
A atividade do Raio X pode ser usada como tarefa de casa ou como avaliação da aula. Envie e faça a discussão da mesma forma que fez com a atividade principal. Lembre-se também que há atividades complementares que podem ser enviadas para os alunos como atividades de fixação ou sistematização.
Convite às famílias
Peça às famílias que, oportunamente, auxiliem na leitura das comandas e no envio das soluções conforme os combinados com o professor. É importante que as famílias acompanhem as atividades nos canais de comunicação estabelecidos entre vocês.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alex de Cassio Macedo
Mentora: Maria Aparecida Nemet
Especialista de área: Fernando Barnabé
Habilidade da BNCC
(EF07MA25) Estabelecer expressões de cálculo de área de triângulos e de quadriláteros.
Objetivos específicos
Analisar a importância das decomposições de figuras planas no cálculo de medidas de superfície (área).
Conceito-chave
Obtenção de expressões para o cálculo de áreas
Recursos necessários
- Folha de papel quadriculado (impressão disponível aqui);
- Atividades impressas em folhas.
- Tesoura, régua, lápis, borracha, caderno.
- Dependendo da preferência do professor pode ser usado retalhos de tecido.
Título do plano - Planos de aula - 7º ano