Aquecimento
Plano de Aula
Plano de aula: Explorando Triângulos Semelhantes
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Semelhança de figuras planas e transformações no espaço.
Por: Eduardo Post
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Eduardo Post
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
Relacionada a EF09MA12 - Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes.
Objetivos específicos
- Compreender o que é semelhança de triângulos.
- Identificar/calcular a razão de semelhança.
- Relacionar a semelhança entre triângulos e movimentos de transformações no espaço.
Conceito-chave
Razão de semelhança em triângulos.
Recursos necessários
Triângulos e tabelas impressos, Régua, Transferidor e Calculadora.
Vocabulário que será adquirido nesta aula
Semelhança entre triângulos, razão de semelhança, ampliação, redução, homotetia.
Habilidades BNCC:
Objetivos de aprendizagem
- Compreender o que é semelhança de triângulos.
- Identificar/calcular a razão de semelhança.
- Relacionar a semelhança entre triângulos e movimentos de transformações no espaço.
Resumo da aula
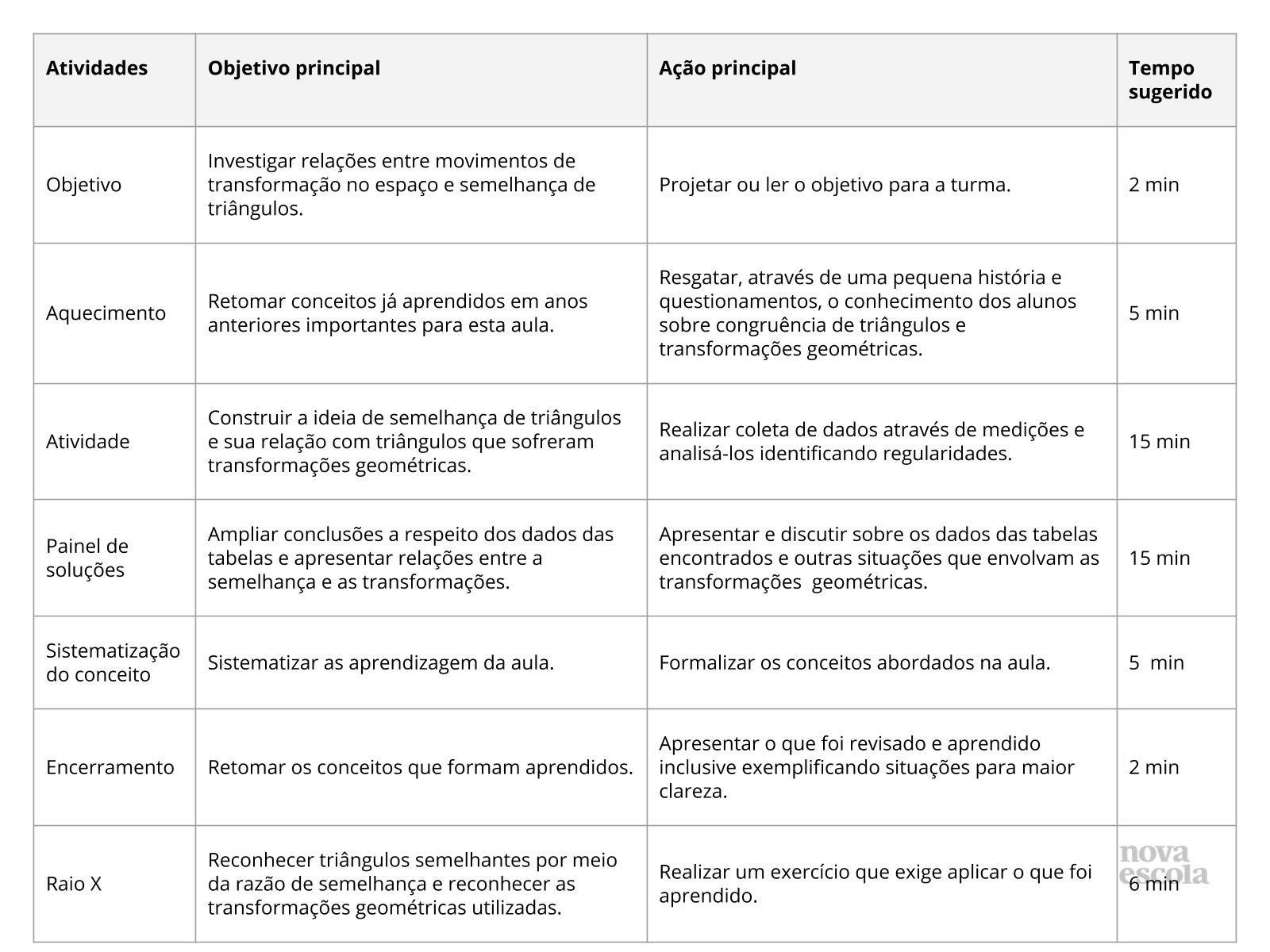
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
<br />Objetivo

Título:
Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
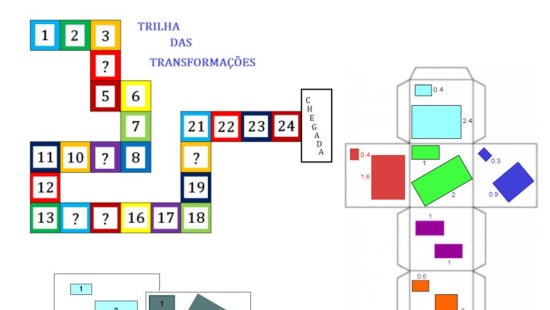
Aquecimento
Título:
Tempo sugerido: 5 minutos (slides 3 e 4).
Orientações: Apresente a história à turma. Peça que digam, em poucas palavras, o que se passa nas imagens.
Propósito: Retomar o conceito de congruência de triângulos e as transformações: reflexão, translação e rotação.
Discuta com a turma:
- A personagem está se olhando no espelho. Qual a diferença entre o triângulo original e o que está no espelho?
Materiais complementares:
Aquecimento
Título:
Tempo sugerido: 5 minutos (slides 3 e 4).
Orientações: Apresente a história à turma. Peça que digam, em poucas palavras, o que se passa nas imagens.
Propósito: Retomar o conceito de congruência de triângulos e as transformações: reflexão, translação e rotação.
Discuta com a turma:
- Qual a diferença entre cada triângulo em cada instante de tempo antes de a personagem tropeçar na escada rolante?
- Qual a diferença dos dois últimos triângulos da escada rolante em relação aos demais?
- Vocês lembram o que é congruência de triângulos? O que precisa acontecer para garantir que triângulos sejam congruentes?
- Os triângulos da história são congruentes?
Materiais complementares:
Atividade Principal
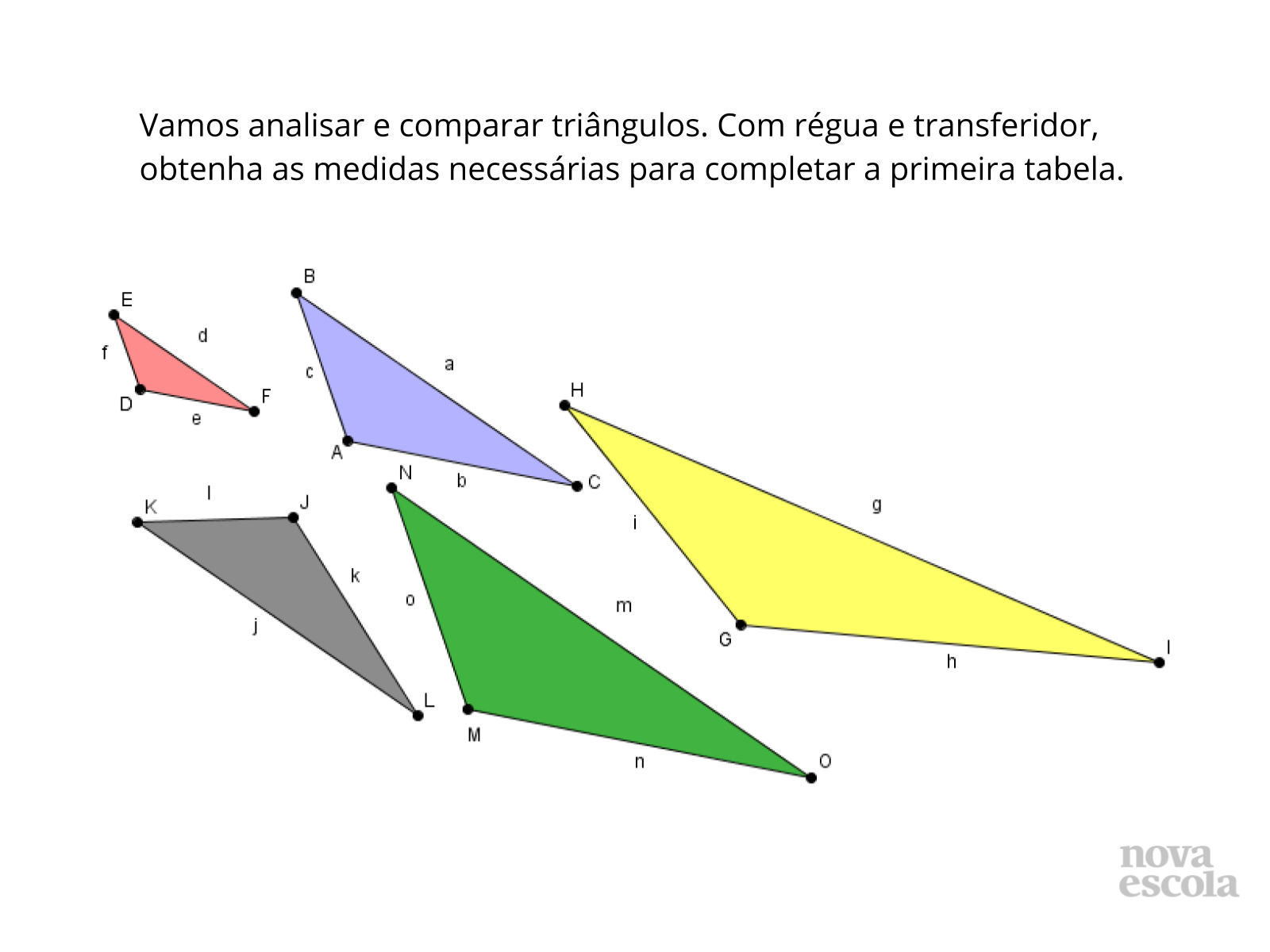
Título:
Tempo sugerido: 15 minutos (slides 5, 6, 7 e 8).
Orientações: Peça que, individualmente, os alunos leiam a atividade e realizem as medições solicitadas na tabela utilizando régua e transferidor. Relembre com os alunos que a soma dos ângulos internos de qualquer triângulo é sempre igual a 180 graus, então devem atentar-se a isso e se for preciso realizar arredondamentos das medidas dos ângulos. Oriente os alunos no preenchimento da segunda tabela. Exemplifique realizando com eles as primeiras razões. As demais razões não estão montadas propositalmente, assim, os alunos precisam identificar os lados correspondentes. Circule na sala e fique atento aos comentários dos alunos, pois podem surgir dúvidas quanto a isso, principalmente no triângulo que não está na mesma posição que o ABC (triângulo JKL). Deixe que discutam com um colega e façam observações. Reserve um tempo para um debate coletivo e deixe que as duplas compartilhem o que discutiram.
Propósito: Identificar que quando as três razões entre lados correspondentes de dois triângulos são iguais, necessariamente os três ângulos correspondentes são congruentes. Além disso, perceber a proporcionalidade nas medidas dos lados dos triângulos que possuem as características citadas anteriormente.
Discuta com a turma:
- Todos os triângulos possuem o mesmo tamanho?
- O que vocês observaram quanto às medidas dos ângulos dos triângulos? E em relação aos resultados das razões?
Materiais complementares:
Atividade Principal
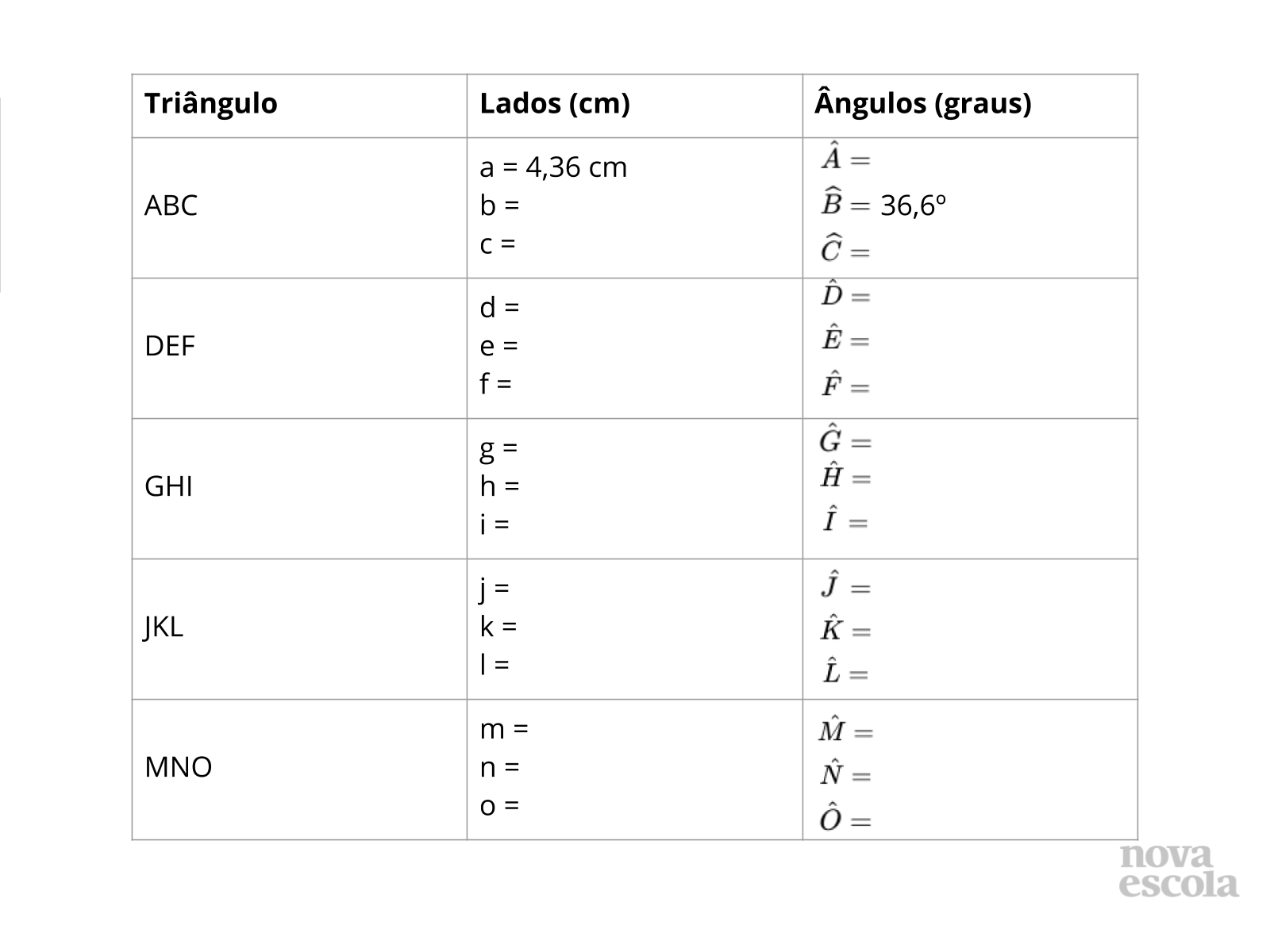
Título:
Tempo sugerido: 15 minutos (slides 5, 6, 7 e 8).
Orientações: Circule na sala e acompanhe o processo de preenchimento da tabela, auxiliando os alunos se for necessário.
Propósito: Verificar se todos entenderam como preencher a tabela.
Materiais complementares:
Atividade Principal

Título:
Tempo sugerido: 15 minutos (slides 5, 6, 7 e 8).
Orientações: Circule na sala e acompanhe o processo de preenchimento da tabela, auxiliando os alunos se for necessário.
Propósito: Verificar se todos entenderam como preencher a tabela.
Materiais complementares:
Atividade Principal

Título:
Tempo sugerido: 15 minutos (slides 5, 6, 7 e 8).
Orientações: Circule na sala e acompanhe o processo de discussão dos alunos, os auxiliando se for necessário.
Propósito: Compartilhar resultados encontrados.
Materiais complementares:
Discussão da Solução
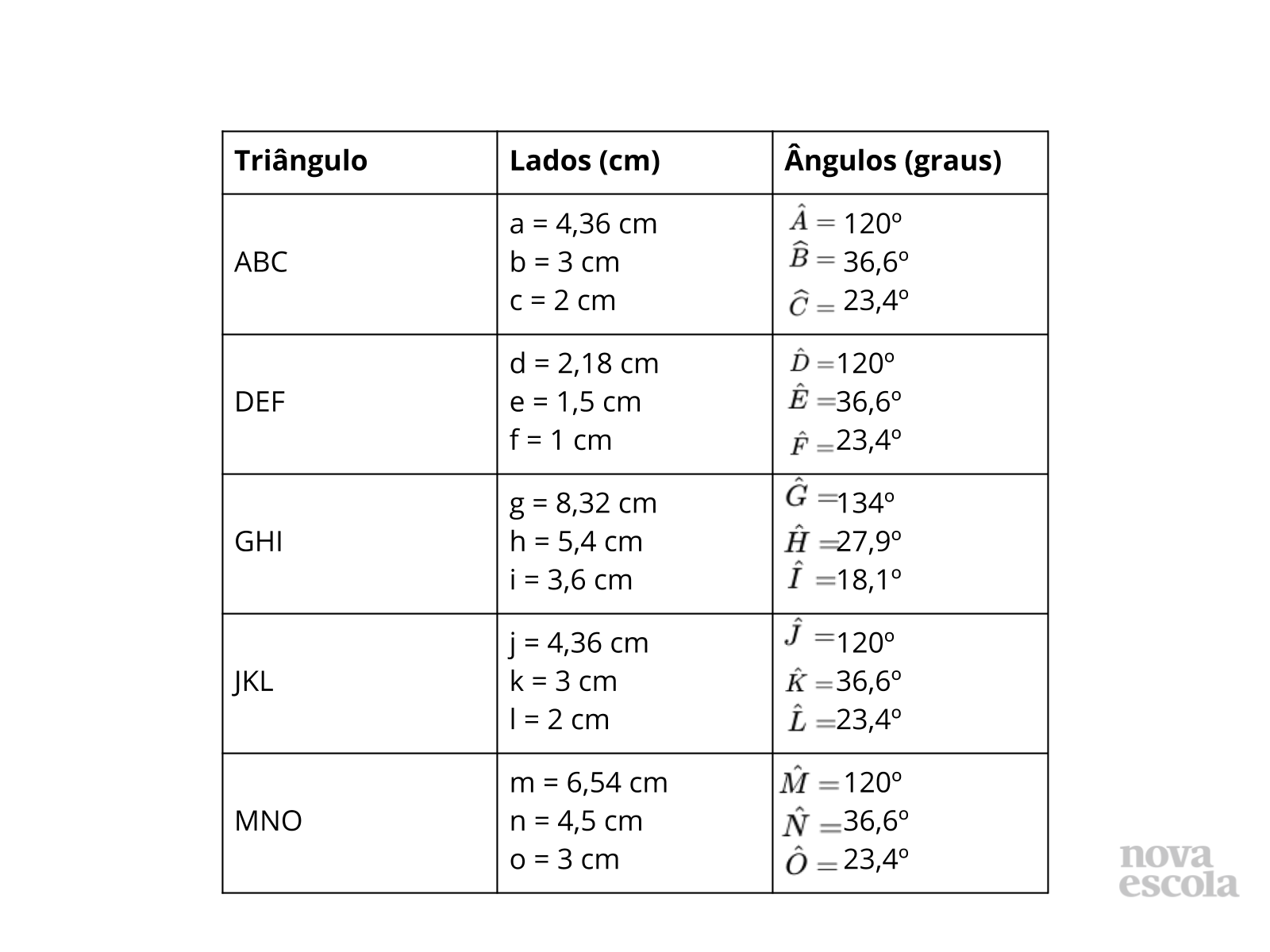
Título:
Tempo sugerido: 15 minutos (slides 9, 10, 11, 12, 13 e 14).
Orientações: Para essa discussão você pode projetar as tabelas preenchidas. Discutindo os valores com a turma, os alunos vão começar a perceber as características de triângulos semelhantes. As construções dos triângulos foram realizadas no GeoGebra, assim, as medidas dos lados expostos nas tabelas podem ser diferentes das encontradas pelos alunos com os triângulos impressos, mas os ângulos e as razões manterão-se os mesmos.
Propósito: Fazer os alunos perceberem que para triângulos serem semelhantes é necessário que os ângulos correspondentes sejam congruentes e os lados correspondentes proporcionais.
Discuta com a turma:
- Analisando os três ângulos em cada triângulo, como podemos mostrar que as medidas fazem sentido? (Relembrar com os alunos que a soma dos ângulos internos de um triângulo é 180º).
Discussão da Solução
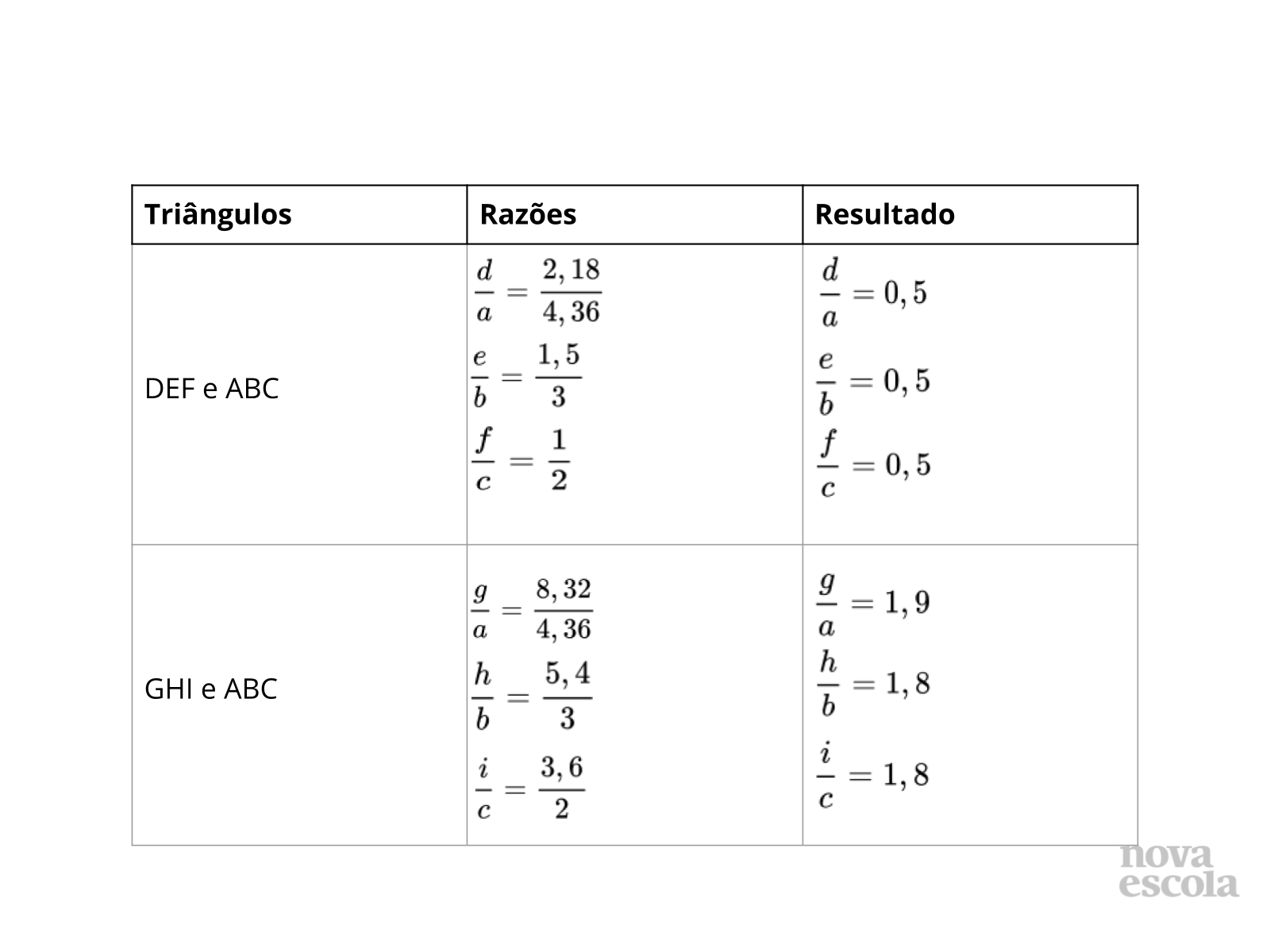
Título:
Tempo sugerido: 15 minutos (slides 9, 10, 11, 12, 13 e 14).
Orientações: Para essa discussão você pode projetar as tabelas preenchidas. Discutindo os valores com a turma, os alunos vão começar a perceber as características de triângulos semelhantes. As construções dos triângulos foram realizadas no GeoGebra, assim, as medidas dos lados expostos nas tabelas podem ser diferentes das encontradas pelos alunos com os triângulos impressos, mas os ângulos e as razões manterão-se os mesmos.
Propósito: Fazer os alunos perceberem que para triângulos serem semelhantes é necessário que os ângulos correspondentes sejam congruentes e os lados correspondentes proporcionais.
Discuta com a turma:
- Analisando os três ângulos em cada triângulo como podemos mostrar que as medidas fazem sentido? (Relembrar com os alunos que a soma dos ângulos internos de um triângulo é 180º).
Discussão da Solução
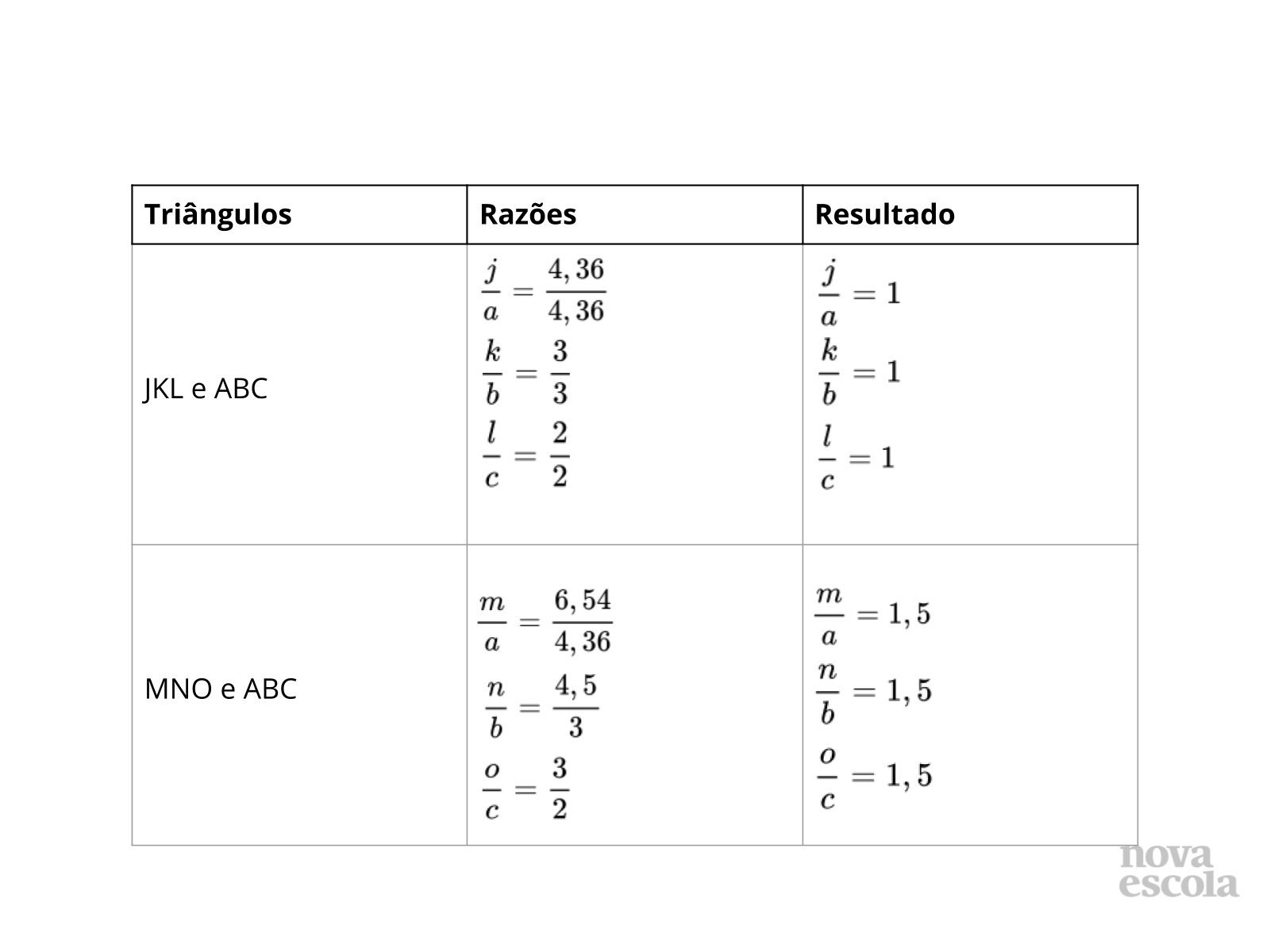
Título:
Tempo sugerido: 15 minutos (slides 9, 10, 11, 12, 13 e 14).
Orientações: Para essa discussão você pode projetar as tabelas preenchidas. Discutindo os valores com a turma, os alunos vão começar a perceber as características de triângulos semelhantes.
Propósito: Fazer os alunos perceberem que para triângulos serem semelhantes é necessário que os ângulos correspondentes sejam congruentes e os lados correspondentes proporcionais.
Discuta com a turma:
- Por quais motivos as razões obtidas na comparação dos triângulos GHI e ABC são diferentes?
- O que podemos observar nas medidas dos lados dos triângulos que tiveram razões sempre iguais?
- Por que as razões das medidas dos lados dos triângulos JKL e ABC resultaram em 1?
- Qual é a relação entre as medidas dos lados dos pares de triângulos comparados e dos valores de suas razões?
Discussão da Solução
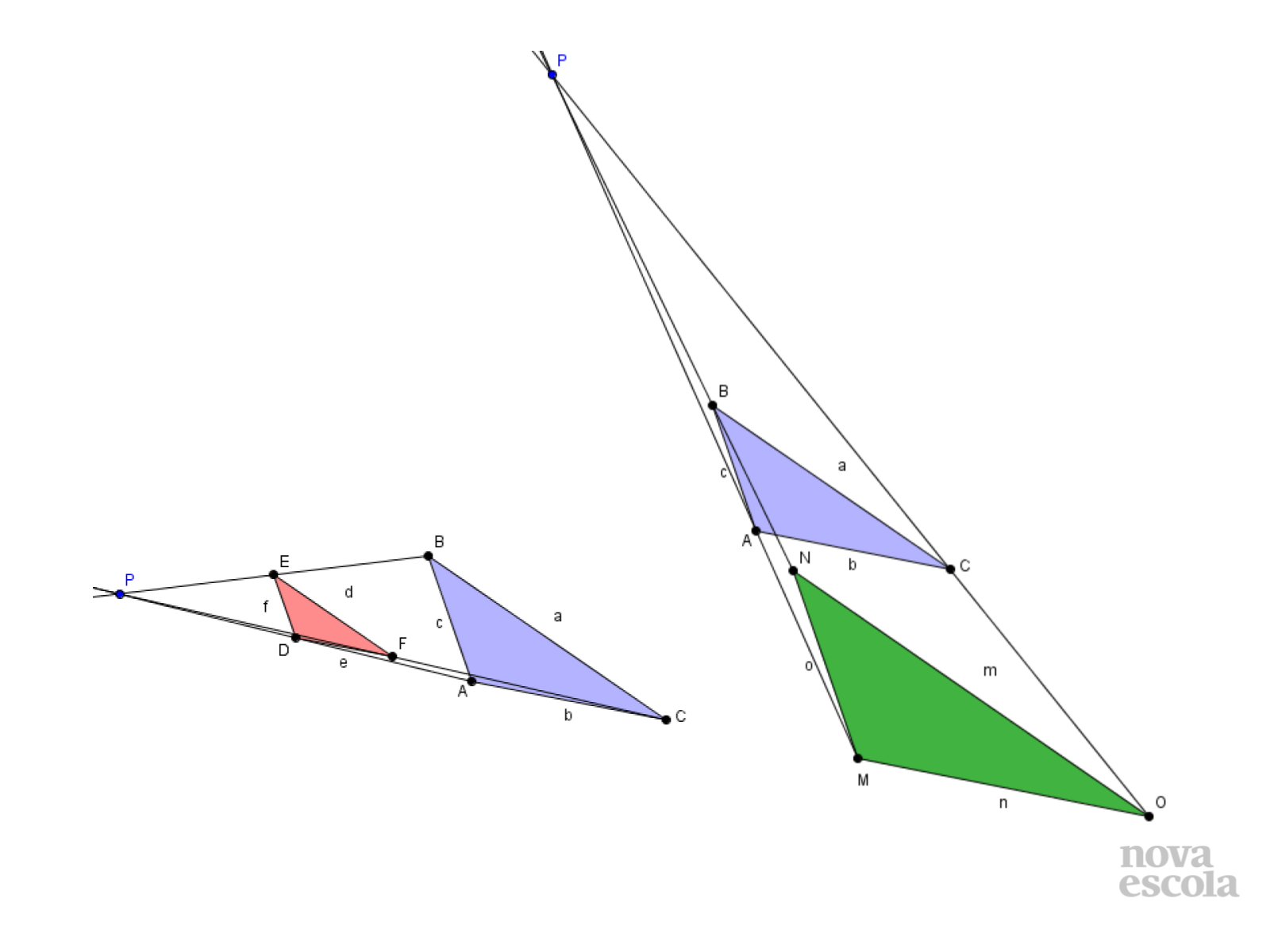
Título:
Tempo sugerido: 15 minutos (slides 9, 10, 11, 12, 13 e 14).
Orientações: Apresente aos alunos os mesmos triângulos da atividade, mas agora com semirretas passando pelos vértices correspondentes. Analisem juntos as figuras e peça que os alunos comentem o que observaram. Você pode solicitar que eles também representem essas semirretas para que possam realizar medições de segmentos e concluírem que, no triângulo DEF, PD=2PA e o mesmo ocorre com os outros vértices. O número 2 é que determina a razão de semelhança. Comente que o triângulo DEF é uma redução do triângulo ABC. Como discutido ao fazer a análise das tabelas, as medidas dos lados do triângulo DEF foram reduzidas à metade, por isso a razão é 1/2=0,5. Já no triângulo MNO, PA=1,5PM. Essa relação pode tornar-se mais clara ao pensar que PA cabe uma vez e meia sobre PM. Assim a razão de semelhança é 1,5 e o triângulo MNO é uma ampliação do triângulo ABC.
Propósito: Relacionar o conceito de semelhança de triângulos com as transformações: redução e ampliação.
Discuta com a turma:
- O que acontece quando traçamos as semirretas?
- Que relação podemos escrever a respeito dos segmentos PD e PA? E nos segmentos determinados pelos outros vértices do triângulo DEF?
- Que relação podemos escrever a respeito dos segmentos PA e PM? E nos segmentos determinados pelos outros vértices do triângulo MNO?
- Compare essas relações com as razões dos lados desses triângulos da tabela. O que podemos observar?
Discussão da Solução
Título:
Tempo sugerido: 15 minutos (slides 9, 10, 11, 12, 13 e 14).
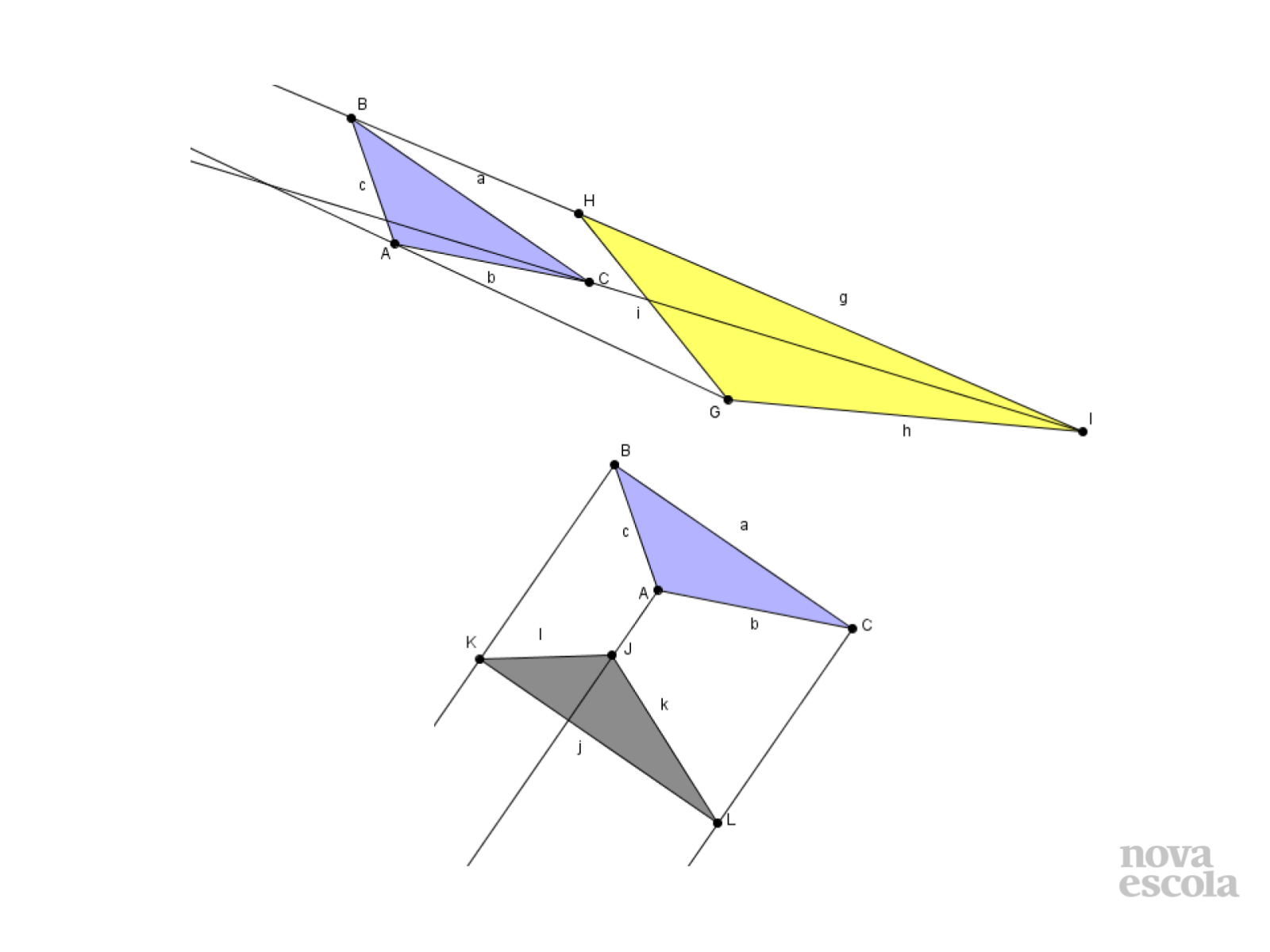
Orientações: Faça o mesmo com os demais pares de triângulos da atividade. Analisem juntos as figuras e peça que os alunos comentem o que observaram.
Propósito: Perceber que o triângulo GHI não é uma ampliação de ABC e que o triângulo JKL é semelhante à ABC mas não foi obtido por redução ou ampliação (homotetia), mas possui o mesmo tamanho, ou seja, é congruente ao triângulo ABC.
Discuta com a turma:
- Por que no triângulo GHJ as semirretas não se interceptam no mesmo ponto? Qual a diferença em relação aos outros dois?
- Os triângulos JKL e ABC possuem as características de triângulos semelhantes? Por que as semirretas não se interceptaram no mesmo ponto?
- Existe alguma diferença entre os triângulos ABC e JKL?
- Através de qual transformação geométrica o triângulo JKL foi originado?
Discussão da Solução
Título:
Tempo sugerido: 15 minutos (slides 9, 10, 11, 12, 13 e 14).
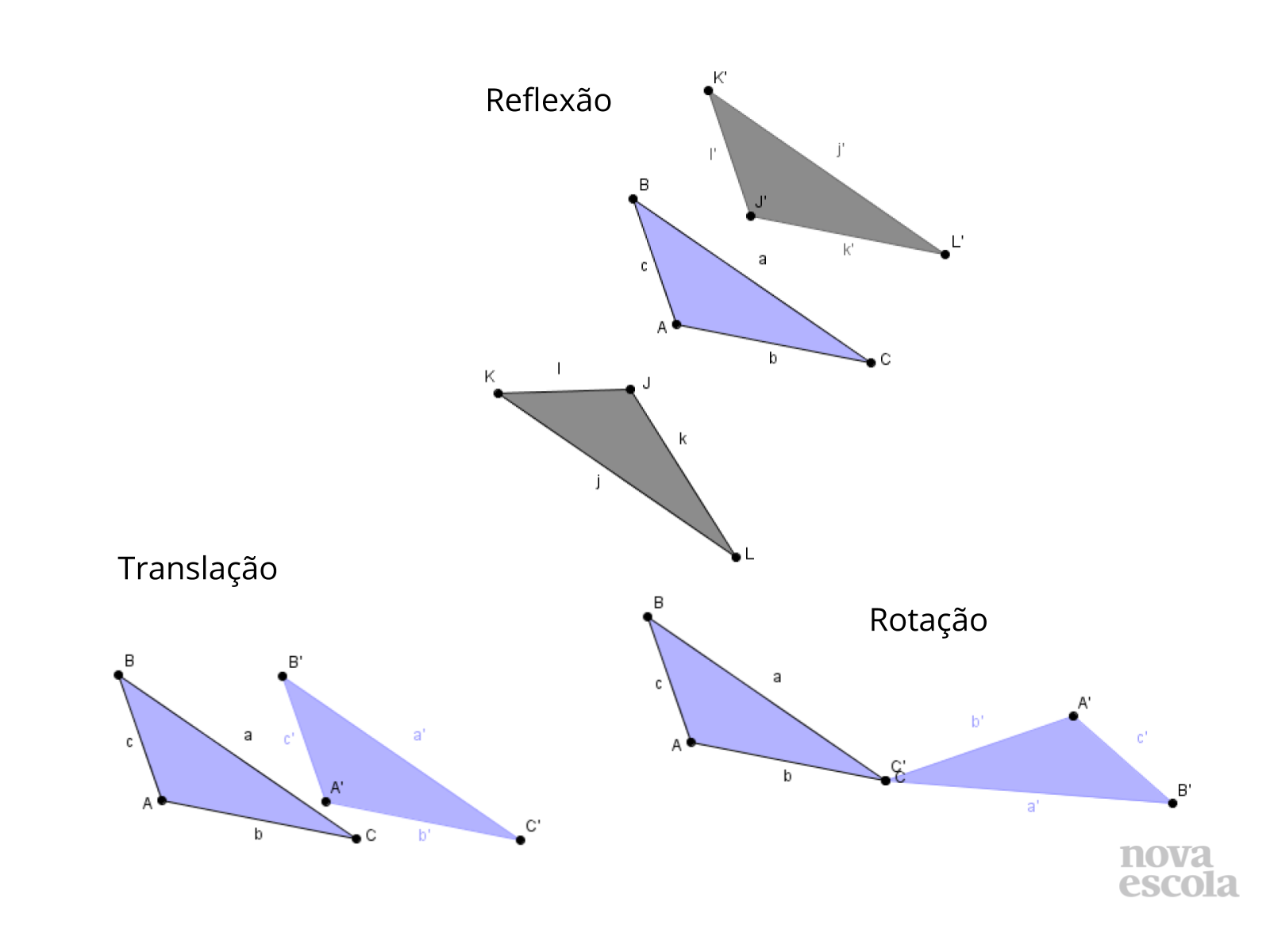
Orientações: Apresente também as transformações geométricas que não alteram o tamanho da figura: translação, rotação e reflexão. Neste momento, os alunos já perceberam que triângulos congruentes possuem todas as características de triângulos semelhantes em função da análise do triângulo JKL, que neste slide foi refletido para ficar na mesma posição que ABC e facilitar a percepção de que são congruentes.
Propósito: Perceber que todos os triângulos congruentes são também semelhantes de razão 1 e que as transformações: translação, rotação e reflexão alteram apenas a posição das figuras, originando figuras congruentes e, consequentemente, semelhantes.
Discuta com a turma:
- Qual a diferença entre os triângulos originados por essas transformações e o triângulo ABC?
Sistematização do Conceito

Título:
Tempo sugerido: 5 minutos.
Orientações: Formalize os conceitos que foram aprendidos nesta aula. Você pode, ainda, perguntar aos alunos se estas características são satisfeitas por outros pares de triângulos da atividade que não, comparado-os na tabela. Retome também a palavra homotetia. As transformações por homotetia são a redução e a ampliação. Utilize este termo para que os alunos o conheçam.
Propósito: Apresentar os conceitos relacionados à atividade principal.
Encerramento

Título:
Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade retomando com os estudantes o que foi aprendido nesta aula. Peça que leiam a conclusão e registrem no caderno.
Propósito: Retomar os conceitos que foram aprendidos.
Raio X
Título:
Tempo sugerido: 6 minutos.
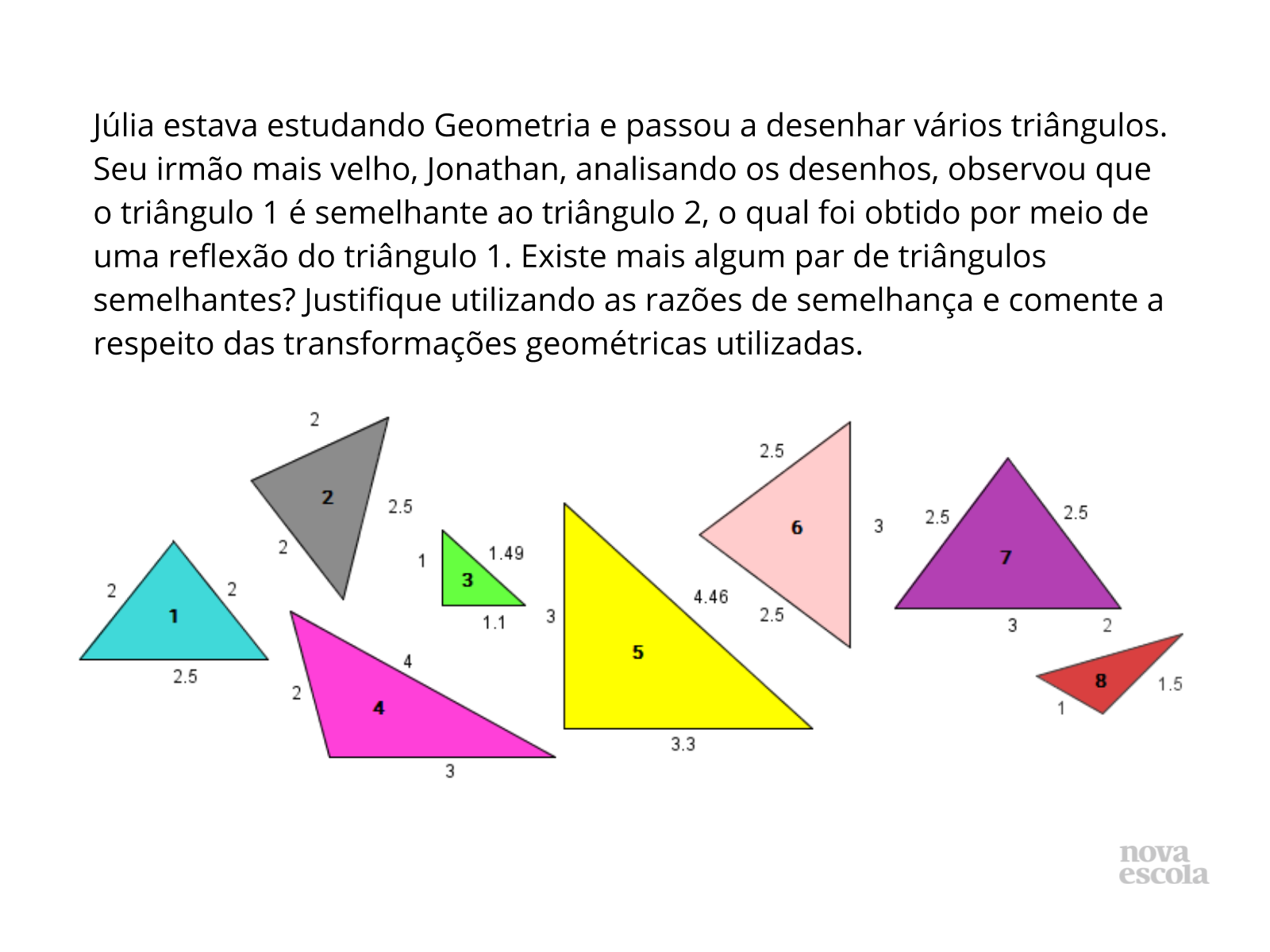
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo, registrando as soluções na lousa.
Propósito: Auxiliar os alunos a perceber que somente o formato parecido da figura não é suficiente para verificar a semelhança. O mais importante é conseguir justificar a semelhança matematicamente.
Discuta com a turma:
- Existe um padrão nas medidas dos lados correspondentes dos triângulos 1 e 7?
- Esse é o mesmo padrão que ocorre quando as figuras são semelhantes?
- Qual é a diferença entre o que ocorreu nesses triângulos e o que ocorre em um par de triângulos semelhantes qualquer?
Materiais complementares:
Sugestão de adaptação para ensino remoto
Código do plano (MAT9_12GEO02)
Ferramentas sugeridas
- Essenciais: Alguma rede social (Whatsapp, Facebook, etc.) e papel para anotações.
- Optativas: Calculadora.
Aquecimento
- Pela rede social escolhida, inicie esse contato questionando se seus alunos e alunas lembram das condições de semelhança dos retângulos de um contato anterior. E diga que agora chegou a vez de observar os triângulos.
Atividade principal
- Determine que, acessem o Geogebra (instalado no PC ou online pelo link https://www.geogebra.org/classic?lang=pt_PT)
- Agora solicite que sigam os passos abaixo:
1. Retire a malha quadriculada e os eixos na opção “malha” e “eixos” que aparece quando se clica com o botão direito do mouse na tela das coordenadas.
2. Construa um triângulo qualquer. Utilize a opção: polígono. Aparecerão os vértices A, B e C.
3. Com a opção “ângulo” construa os ângulos internos do triângulo clicando nos pontos nessa ordem: ABC, BCA e CAB.
4. Usando a opção RETA PARALELA, construa retas paralelas aos lados do triângulo fazendo-as gerar um triângulo com tamanho diferente do inicial. Após isso, se for necessário, diminua o zoom da tela.
5. Usando a opção POLÍGONO construa o triângulo, já limitado pelas retas paralelas.
6. Com a opção “ângulo” construa os ângulos internos do outro triângulo.
7. Usando a opção RETA, construa retas que liguem os vértices correspondentes dos triângulos e verifique se elas se cruzam em um único ponto e marque-o usando a opção PONTO.
8. Com a opção SEGMENTO, trace segmentos por cima dos lados dos triângulos e veja os valores na janela da álgebra.
9. Com a opção MOVER, representado pela seta, movimente os pontos e veja o que acontece com os ângulos e com os valores.
Discussão das soluções
- Na discussão das soluções, questione sobre o padrão observado em relação aos lados correspondentes e destaque que a razão entre eles é constante, considerando a aproximação até a primeira casa decimal devido à limitação do programa e da destreza humana.
Sistematização e encerramento
- Faça uma sistematização destacando que a semelhança de triângulos já é verificada quando observamos uma dessas condições: ângulos são congruentes ou os lados correspondentes são proporcionais. Pois, se uma condição acontece a outra também ocorre no caso dos triângulos. Lembre que a razão de semelhança é o quociente entre o comprimento de um lado da figura transformada e o comprimento do lado correspondente da figura original.
Convite às famílias
Peça para que seus alunos envolvam seus familiares, próximos neste momento, e relatem suas explorações sobre os desenhos e links acessados.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Eduardo Post
Mentor: Lara Martins Barbosa
Especialista de área: Pricilla Mendes Cerqueira
Habilidade da BNCC
Relacionada a EF09MA12 - Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes.
Objetivos específicos
- Compreender o que é semelhança de triângulos.
- Identificar/calcular a razão de semelhança.
- Relacionar a semelhança entre triângulos e movimentos de transformações no espaço.
Conceito-chave
Razão de semelhança em triângulos.
Recursos necessários
Triângulos e tabelas impressos, Régua, Transferidor e Calculadora.
Vocabulário que será adquirido nesta aula
Semelhança entre triângulos, razão de semelhança, ampliação, redução, homotetia.