Atividade principal
Plano de Aula
Plano de aula: Medida de volume por meio de empilhamento de cubos
Plano 1 de uma sequência de 5 planos. Veja todos os planos sobre Medição do volume de cubo e paralelepípedo
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alexandre Tolentino de Carvalho
Mentor: Fábio Menezes da Silva.
Especialista de área: Fernando Barnabé
Habilidade da BNCC
EF05MA21 - Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por meio de empilhamento de cubos, utilizando, preferencialmente, objetos concretos.
Objetivos específicos
- Reconhecer volume como espaço ocupado por um objeto podendo ser medido por meio de empilhamento de cubos
Conceito-chave
Medida de volume por meio de empilhamento de cubos
Recursos necessários
Lápis, borracha e caderno, objetos do cotidiano (caixas, embalagens, dados).
Habilidades BNCC:
Objetivos de aprendizagem
- Reconhecer volume como espaço ocupado por um objeto podendo ser medido por meio de empilhamento de cubos
Resumo da aula
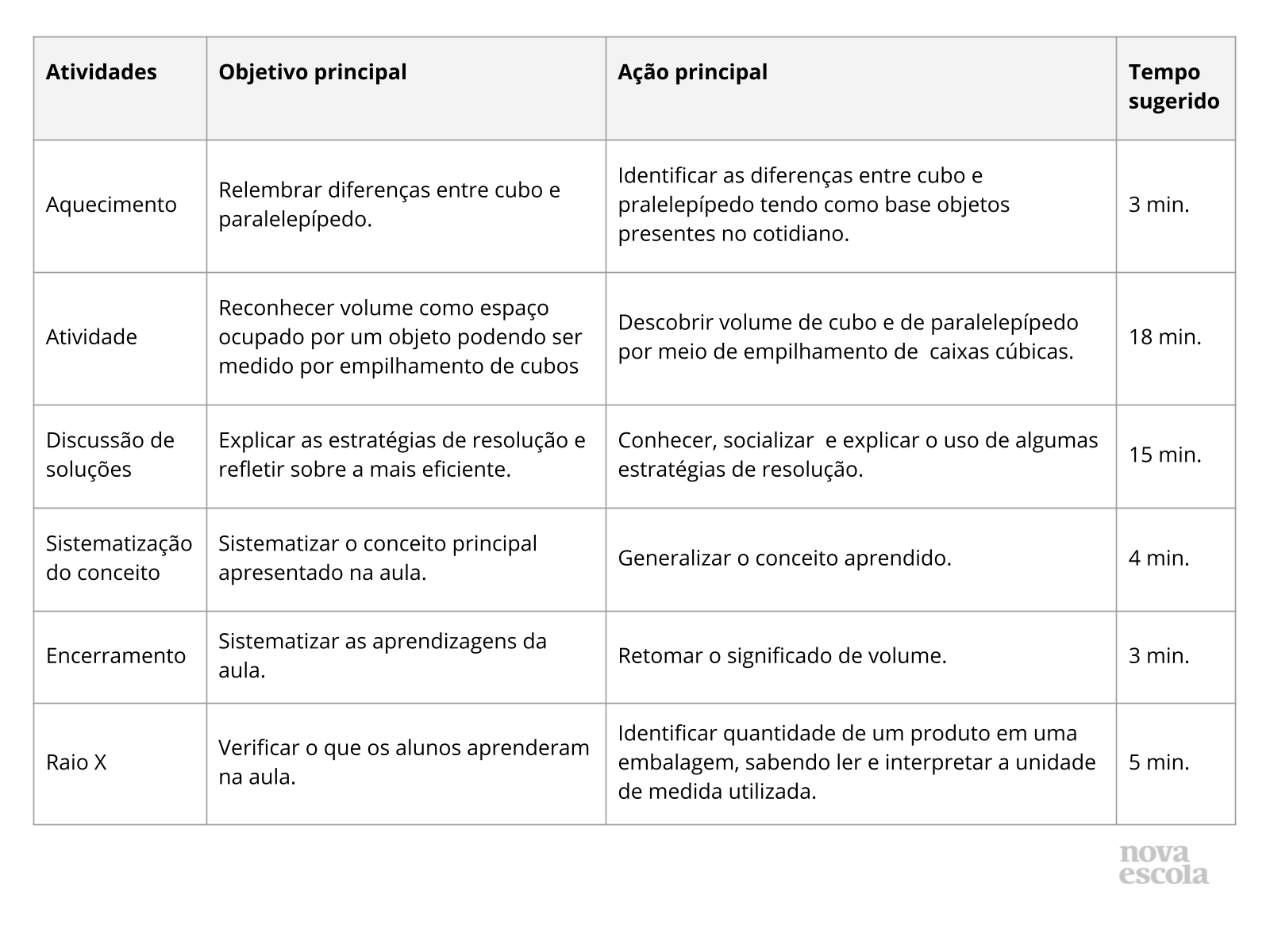
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 3 minutos.
Orientação: Pretende-se que os alunos recordem que a primeira caixa tem formato de cubo e a segunda de paralelepípedo retangular. Chame atenção para o fato de que o cubo também é um paralelepípedo, no entanto recebe um nome especial. Os paralelepípedos podem ser considerados como um tipo especial de prisma em que as faces e bases são formadas por paralelogramos. Busque deixar a turma à vontade para levantar conjecturas e apresentar sua ideias sobre a diferenciação entre os dois sólidos geométricos. A diferenciação e o levantamento de semelhanças será importante para, mais adiante, o aluno estabelecer relações entre o volume desses dois sólidos. É interessante que percebam que os dois sólidos possuem mesma quantidade de faces, de vértices e de arestas. Precisam ainda se conscientizar que as diferenças residem nas formas das faces (cubos são formados por faces quadradas e paralelepípedos retangulares por pelo menos quatro faces retangulares podendo existir faces quadradas ou não) e nas medidas das dimensões (cubos possuem as três dimensões iguais, altura, largura e espessura, e paralelepípedos possuem pelo menos uma dimensão diferente).
Propósito: Relembrar alguns conceitos prévios importantes para as aprendizagens propostas nessa aula.
Discuta com a turma:
- Como poderia chamar os formatos dessas duas caixas?
- O que esses dois formatos têm em comum?
- Em quais critérios podemos pensar para encontrar as diferenças e semelhanças?
- Vocês poderiam citar outros objetos que possuem os formatos dessas caixas?
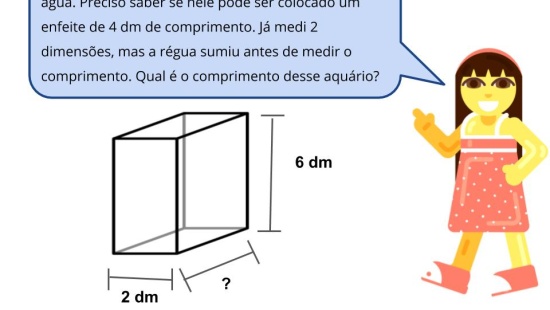
Atividade principal
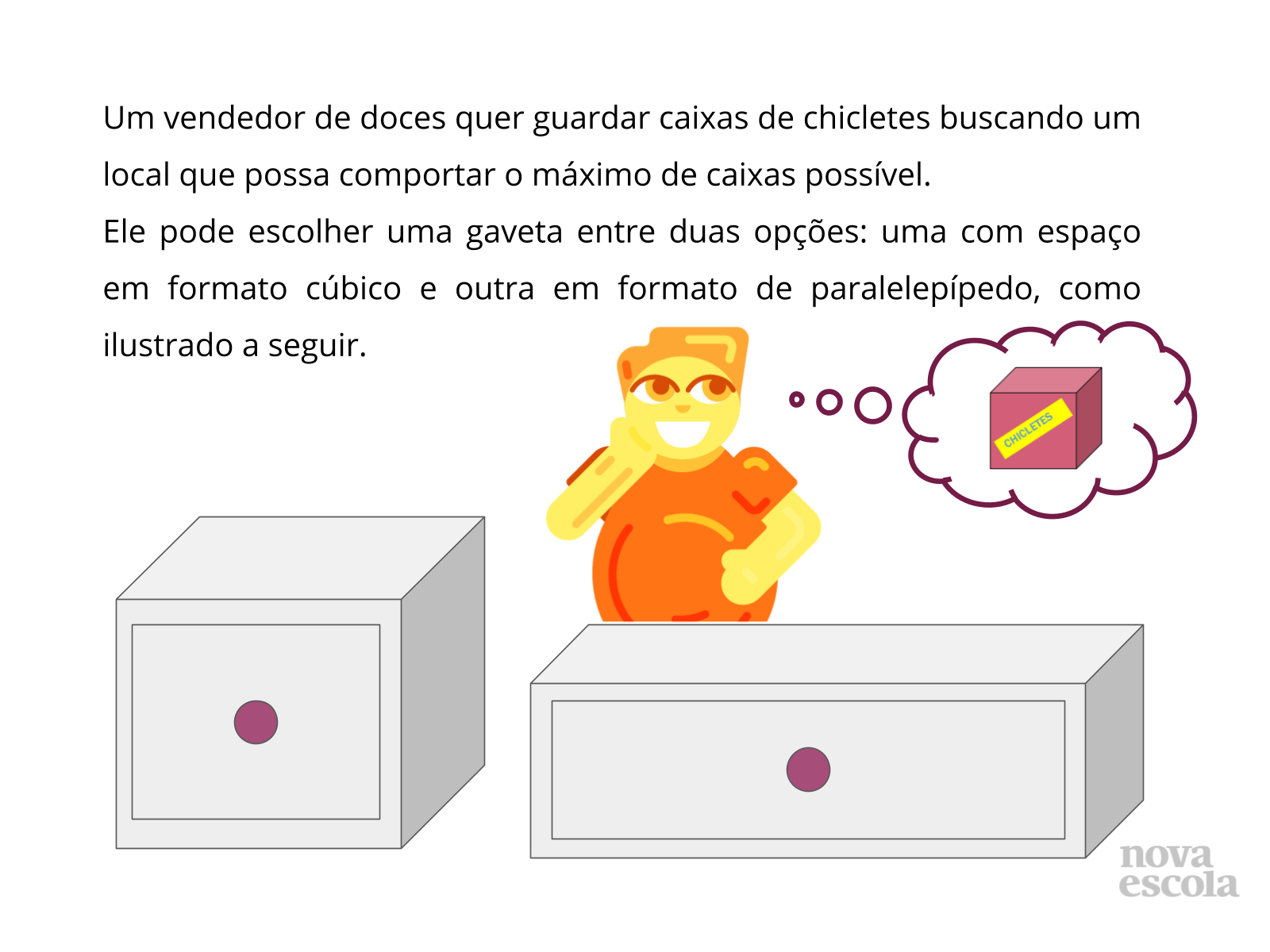
Tempo sugerido: 18 minutos (slides de 4 a 6).
Orientação: Nessa atividade, é interessante que os alunos tenham à disposição materiais que possam ser manipuláveis (caixas, cubinhos de material dourado, dados, etc). Assim, antes de partirem para o trabalho de abstração no qual tenham que manipular as imagens mentalmente, o uso de materiais concretos pode permitir que eles descubram padrões relacionados ao volume dos sólidos que podem auxiliar e direcionar o trabalho mental com as imagens. Nesse primeiro slide é apresentada uma imagem que não está disponível na atividade impressa. Portanto, sugere-se que seja entregue a atividade xerocopiada para cada aluno para que possam lê-la em duplas buscando compreender o que pedem os comandos. Em seguida, chame a atenção dos alunos para este slide pedindo para que tentem estimar intuitivamente, observando as duas gavetas, em qual delas caberá mais caixas de chicletes. Posteriormente, volte a esse slide discutindo sobre as estimativas pedindo os alunos para rever suas respostas iniciais tendo como base os conhecimentos produzidos. É importante que os alunos percebam que as imagens do próximo slide representam as gavetas vistas como se suas paredes estivessem invisíveis ou como se tivesse tirado um raio-x delas para que seja possível enxergar a quantidade de caixas já colocadas de modo a encontrar a quantidade total de caixas que cabem em cada gaveta.
Propósito: Permitir que os alunos estimem a quantidade de caixas de chiclete que cabe em cada gaveta.
Discuta com a turma:
- Quantas caixas de chicletes vocês acham que cabem em cada gaveta?
- Em qual delas vocês acham que cabem mais caixas?
Atividade principal
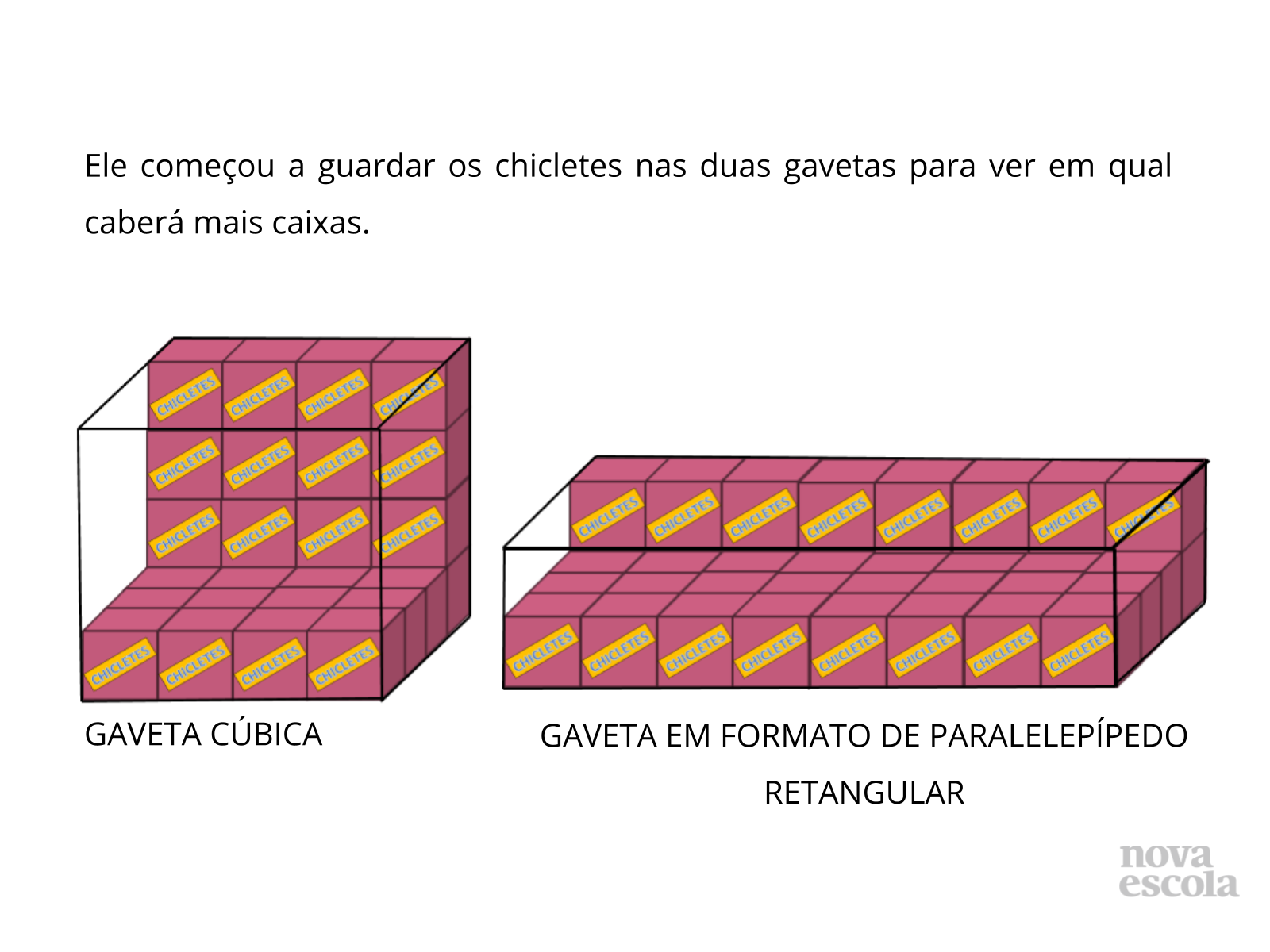
Tempo sugerido: 18 minutos (slides de 4 a 6)
Orientação: Aqui os alunos encontrarão os raio-x das gavetas. É importante que os alunos explorem as imagens de modo a construir estratégias para chegar à quantidade total de caixas possíveis se serem armazenadas em cada gaveta. Nesse sentido, eles precisam exercitar a exploração da imagem em 3 dimensões (altura, largura e espessura) de modo que possam perceber que existem caixas encobertas por outras.
Propósito: Permitir que os alunos consigam, por meio do esforço produtivo, iniciar a exploração da imagem tentando identificar, por meio de uma exploração 3D, a quantidade de caixas já colocadas em cada gaveta e os respectivos totais possíveis de serem armazenados.
Discuta com a turma:
- Quantas caixas vocês podem ver em cada gaveta?
- Que estratégias podem ser utilizadas para chegar nessa quantidade?
- Que detalhes da figura nos permite encontrar a quantidade de caixas já colocadas e nos levar a descobrir a quantidade de caixas possíveis de serem colocadas em cada gaveta?
Atividade principal

Tempo sugerido: 18 minutos (slides de 4 a 6)
Orientação: Peça para os alunos se organizarem em duplas ou trios. Após as discussões anteriores, permita que discutam e registrem as estratégias utilizadas para chegarem à solução do problema. Os materiais manipulativos podem ser deixados à disposição para que os alunos possam recorrer a eles para testar suas hipóteses e confirmar as estratégias utilizadas.
Propósito: Permitir que os alunos consigam, por meio do esforço produtivo, criar estratégias para encontrar o volume de cada sólido para posteriormente compará-los.
Discuta com a turma:
- Sem precisar contar caixa por caixa, que estratégias vocês podem utilizar para chegar ao resultado?
Discussão de soluções

Tempo sugerido: 15 minutos (slides 7 a 13).
Orientações: Permita que os alunos compartilhem suas soluções com os demais colegas de turma. Peça para identificarem semelhanças e as diferentes formas de solucionar a questão. Em seguida, passe para estes slides. Nele, os alunos poderão comparar suas respostas. Ofereça oportunidades para que os alunos possam participar, realizando conexões com os objetos e situações do dia a dia em que são demandados o uso e organização do espaço. Esclareça que todos os objetos, pessoas, animais, materiais diversos possuem volume porque ocupam um lugar no espaço.
Propósito: Utilizar as soluções apresentadas pelos alunos para que compreendam que o volume pode ser medido por meio do empilhamento de cubos.
Discuta com a turma:
- Que tipo de coisas possuem volume?
- Por que essas coisas possuem volume?
- O que podemos fazer para medir o volume de um objeto como as gavetas?
Discussão de soluções
Tempo sugerido: 15 minutos (slides 7 a 13).
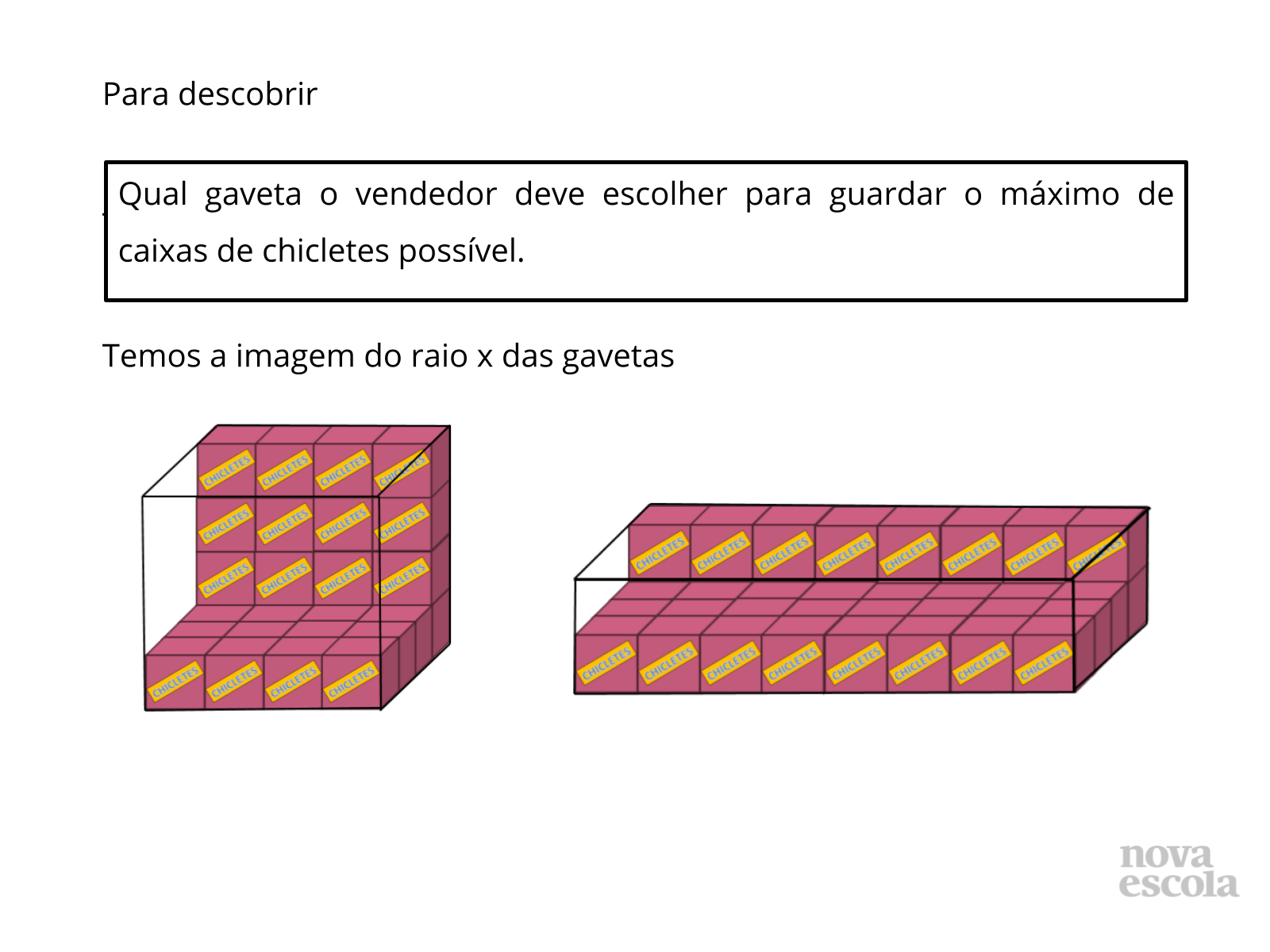
Orientações: Conduza os alunos a perceber que, ao iniciar o armazenamento das caixas, o vendedor começou a ocupar o espaço interno das gavetas. Por isso, a figura mostra o volume parcial das gavetas que pode ser medido pela quantidade de caixas de chiclete já guardadas. Instigue-os a perceber que ainda cabem caixas nas duas gavetas e permita que utilizem várias estratégias para calcular a quantidade de caixas já guardadas e o volume total possível de ser guardado.
Propósito: Utilizar as soluções apresentadas pelos alunos para que compreendam que o volume pode ser medido por meio do empilhamento de cubos.
Discuta com a turma:
- Quantas caixas já foram guardadas?
- Que estratégias vocês utilizaram para chegar a essa quantidade?
- Ainda cabem caixas nas gavetas? Quantas?
- Então, podemos saber quantas caixas cabem ao todo em cada gaveta? Como podemos chegar a esse resultado?
Discussão de soluções
Tempo sugerido: 15 minutos (slides 7 a 13).
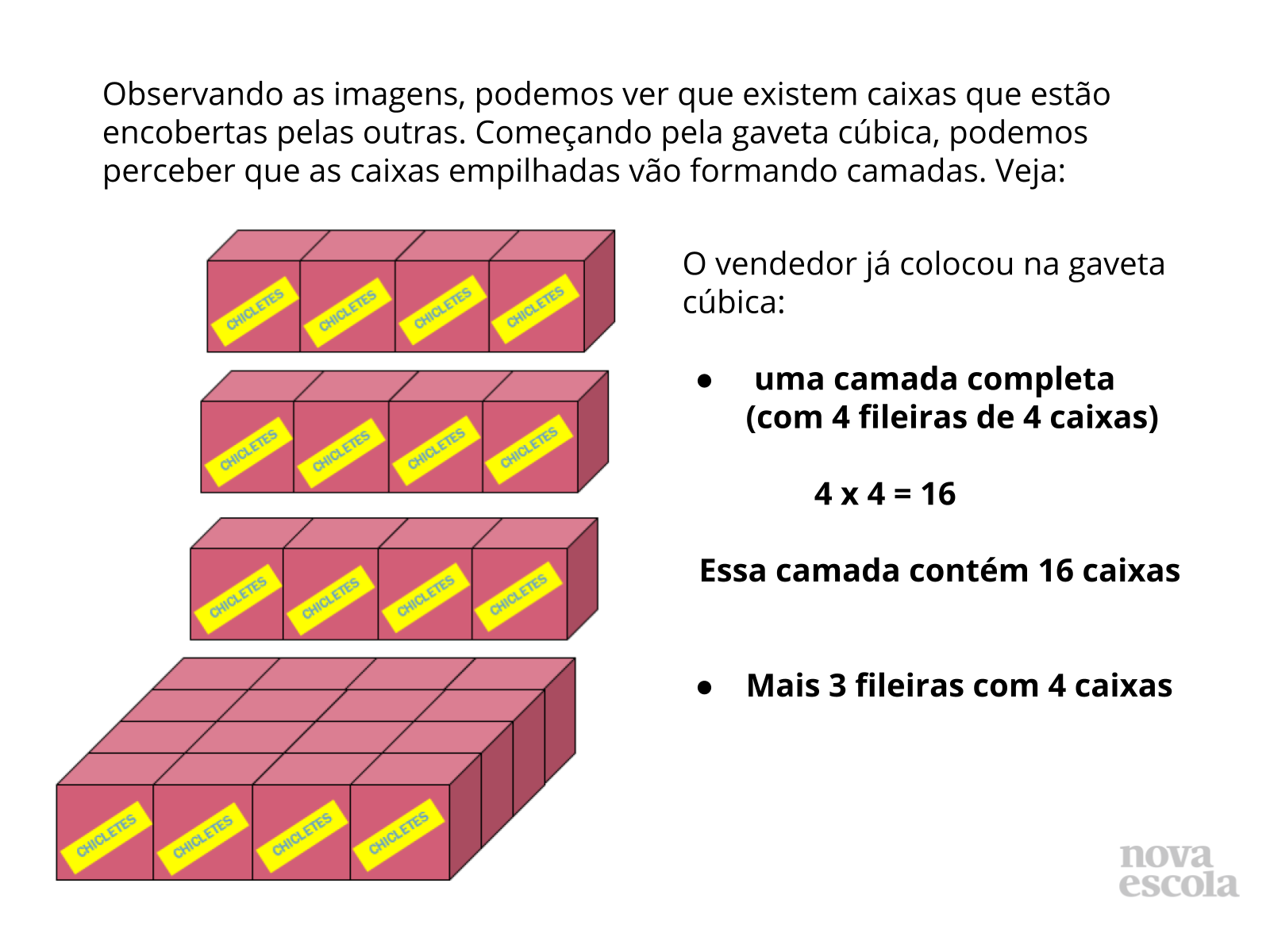
Orientações: Neste slide apresentamos a compartimentação das caixas em camadas para que o aluno perceba a relação multiplicativa geométrica entre o espaço a ser organizado e a disposição escolhida para guardar as caixas. Desse modo, é preciso enfatizar o fato de que as caixas estão organizadamente empilhadas fazendo com que o espaço seja ocupado completamente. Nesse sentido, caso as caixas fossem jogadas dentro da gaveta uma sobre a outra sem organização, além de dificultar a contagem, caberiam menos caixas devido à ocupação desordenada do espaço. Assim, a apresentação da imagem tem o objetivo de demonstrar o sentido multiplicativo geométrico entendido pelo fato de que, em todas as camadas, há quantidades iguais de caixas que podem ser calculadas pela multiplicação da quantidade de caixas em cada fileira pela quantidade total de fileiras de cada camada.
Propósito: Utilizar as soluções apresentadas pelos alunos para que compreendam que o volume pode ser medido por meio do empilhamento de cubos.
Discuta com a turma:
- Essas caixas estão empilhadas de forma organizada?
- O que aconteceria caso fossem guardadas sem organização?
- Como foi feita essa organização?
- Esse empilhamento contém fileiras com mesmo quantidade de caixas em cada fileira?
- Então, que operação podemos realizar para chegar ao total de caixas em cada camada?
Discussão de soluções
Tempo sugerido: 15 minutos (slides 7 a 13).
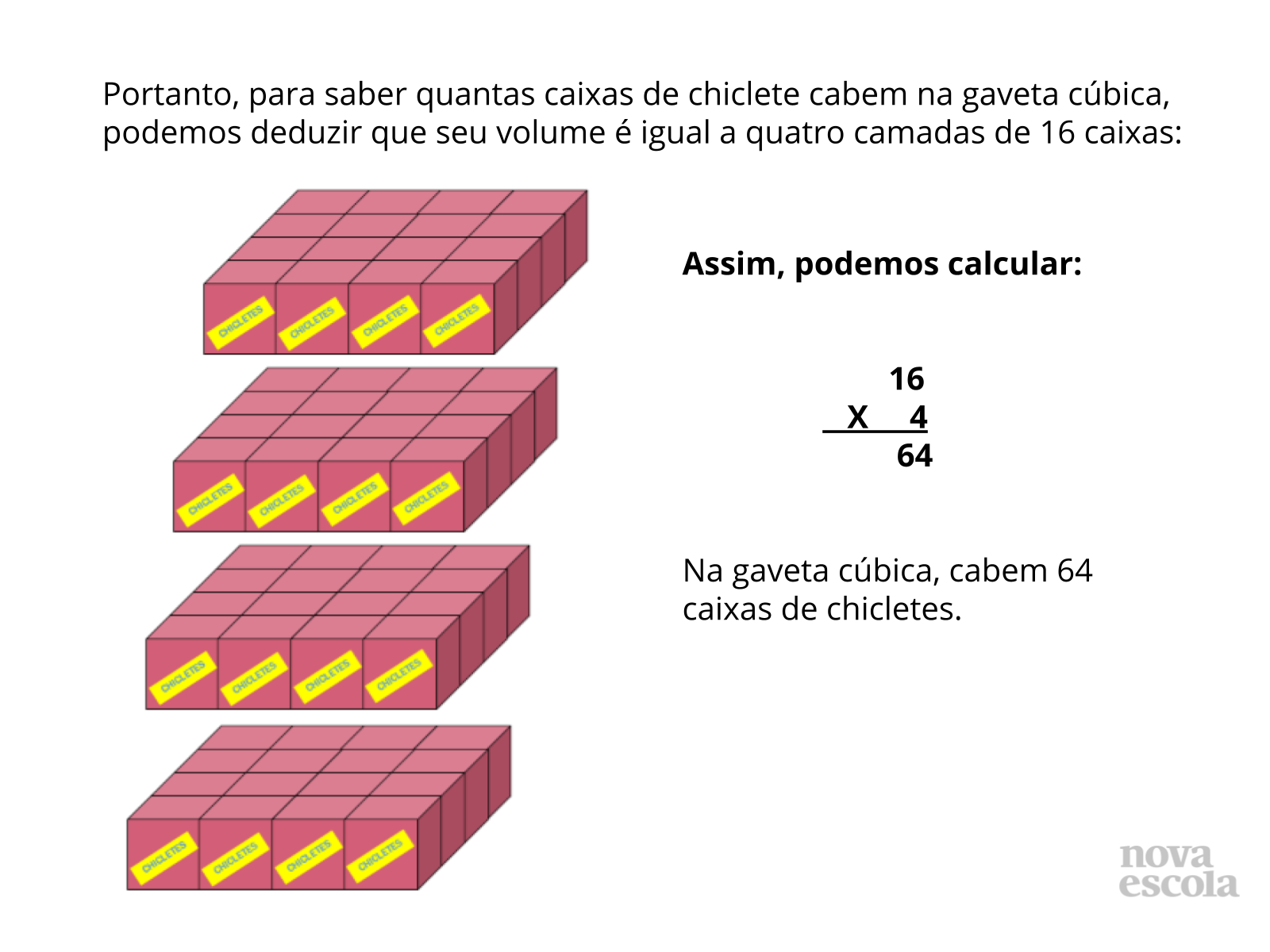
Orientações: Aqui são apresentadas as camadas completas. Leve os alunos a concluir que todas as camadas possuem a mesma quantidade de fileiras com a mesma quantidade de caixas. Essa organização somente é possível de realizar devido ao formato da gaveta. Particularmente, seu formato cúbico apresenta o padrão no qual a quantidade de caixas em cada fileira (4) é igual à quantidade total de fileiras em cada camada (4) que é igual à quantidade de camadas totais (4). É interessante que os alunos percebam esse padrão que será útil, mais tarde, para compreender a fórmula para calcular volume do cubo (aresta elevado a 3). Portanto, para calcular a quantidade total total de caixas, basta multiplicar o total de caixas em cada camada (16) pelo total de camadas (4).
Propósito: Utilizar as soluções apresentadas pelos alunos para que compreendam que o volume pode ser medido por meio do empilhamento de cubos.
Discuta com a turma:
- Quantas camadas cabem ao todo nessa gaveta?
- As camadas têm a mesma quantidade de caixas?
- Então, que estratégia podemos utilizar para chegar no total de caixas que cabem nessa gaveta?
- O que há de comum em relação a quantidade de caixas em cada fileira, a quantidade de fileiras em cada camada e a quantidade de camadas que cabem na gaveta?
- O que você pode perceber em relação às duas multiplicações que foram feitas para chegar ao resultado final?
Discussão de soluções
Tempo sugerido: 15 minutos (slides 7 a 13).
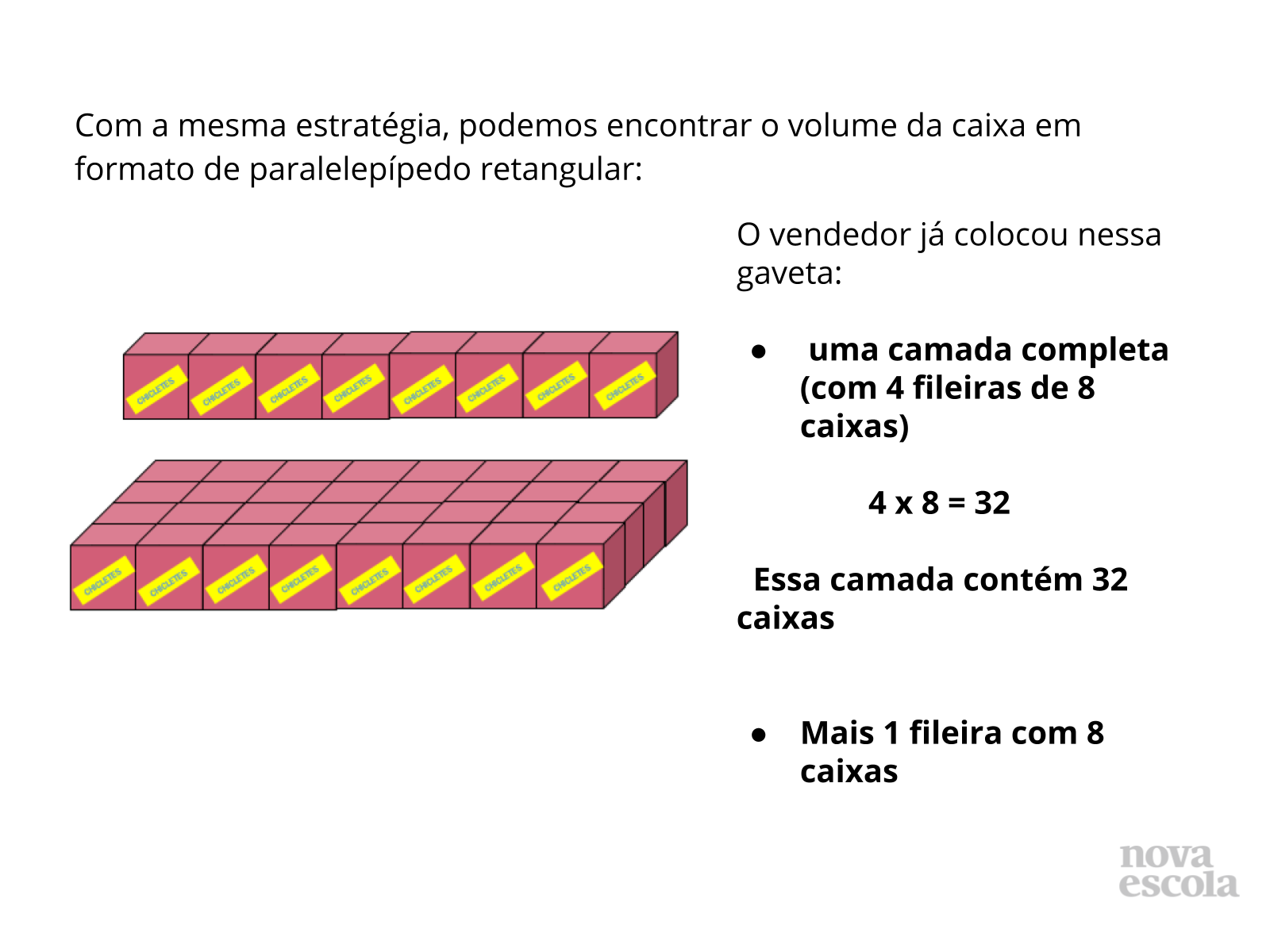
Orientações: Na segunda gaveta, os slides levarão os alunos a perceber a diferença entre as dimensões do paralelepípedo retangular. Aqui o aluno perceberá que, diferentemente da gaveta cúbica, as fileiras serão formadas por 8 caixas e as camadas serão formadas por 4 fileiras com 8 caixas. Por isso a multiplicação 8 x 4.
Propósito: Utilizar as soluções apresentadas pelos alunos para que compreendam que o volume pode ser medido por meio do empilhamento de cubos.
Discuta com a turma:
- E nessa gaveta? Quantas caixas cabem em cada fileira?
- E quantas fileiras formam uma camada?
- Com essas informações, o que poderemos fazer para encontrar o total de caixas em cada camada?
Discussão de soluções
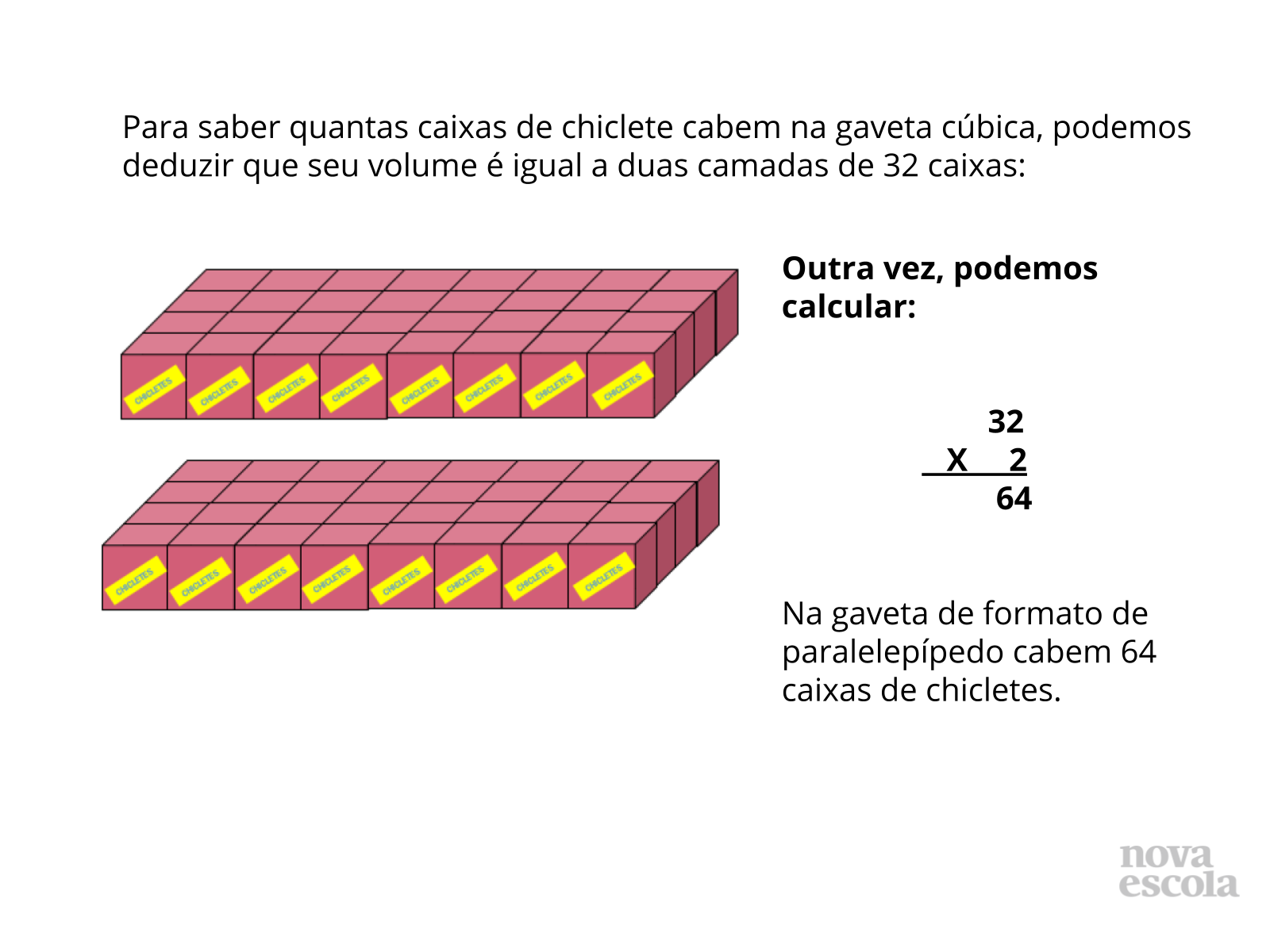
Tempo sugerido: 15 minutos (slides 7 a 13).
Orientações: Após encontrar o total de caixas em cada camada, semelhantemente à estratégia utilizada no caso da gaveta cúbica, os alunos precisam perceber que na gaveta é possível empilhar duas camadas de caixas com 32 caixas. Por isso, basta multiplicar 32 x 2. Perceba que toda a aula foi conduzida de modo a levar os alunos a estabelecer correspondência entre os termos utilizados (caixas por fileiras, fileiras por camadas e camadas por gaveta) e as três dimensões (largura, espessura e altura), mesmo que não seja falado em dimensões, algo que o professor pode julgar pertinente ou não para tratar nesse momento, a ideia ajudará os alunos a descobrir padrões na estipulação do volume do cubo e do paralelepípedo retangular úteis para a compreensão das dimensões como medidas utilizadas no cálculo de volume.
Propósito: Utilizar as soluções apresentadas pelos alunos para que compreendam que o volume pode ser medido por meio do empilhamento de cubos.
Discuta com a turma:
- Quantas camadas de 32 caixas cabem nessa gaveta?
- As camadas têm a mesma quantidade de caixas?
- Então, que estratégia podemos utilizar para chegar no total de caixas que cabem nessa gaveta?
- O que você pode perceber em relação à quantidade de caixas em cada fileira, a quantidade de fileiras em cada camada e a quantidade de camadas da gaveta?
Discussão de soluções

Tempo sugerido: 15 minutos (slides 7 a 13).
Orientações: Após calcular a quantidade de caixas em cada gaveta, os alunos irão realizar a comparação percebendo que, apesar das caixas apresentarem formatos distintos, as duas comportam exatamente a mesma quantidade de caixas de chiclete. É importante que o professor retome as estimativas iniciais promovendo uma reflexão sobre as aproximações e distanciamentos das soluções reais. Inicialmente, alguns dos alunos poderiam ter julgado que na primeira gaveta caberiam mais caixas devido a ser mais alta que a outra. Outros podem ter achado que achado que na gaveta em formato de paralelepípedo retangular caberiam mais caixas por ser mais comprida.
Propósito: Utilizar as soluções apresentadas pelos alunos para que compreendam que o volume pode ser medido por meio do empilhamento de cubos.
Discuta com a turma:
- Qual caixa o vendedor deve escolher?
- Essa resposta condiz com a estimativa inicial de vocês?
- O que levou vocês a realizarem essa estimativa?
Sistematização do conceito

Tempo sugerido: 4 minutos.
Orientações: Aproveite esse momento para permitir que o aluno generalize suas aprendizagens construídas no decorrer da aula.
Propósito: Sistematizar os principais conceitos apresentados no decorrer da aula.
Encerramento

Tempo sugerido: 3 minutos.
Orientações: A aula deve ser concluída com a retomada dos principais conhecimentos pretendidos.
Propósito: Concluir a aula resumindo os conhecimentos produzidos.
Raio X
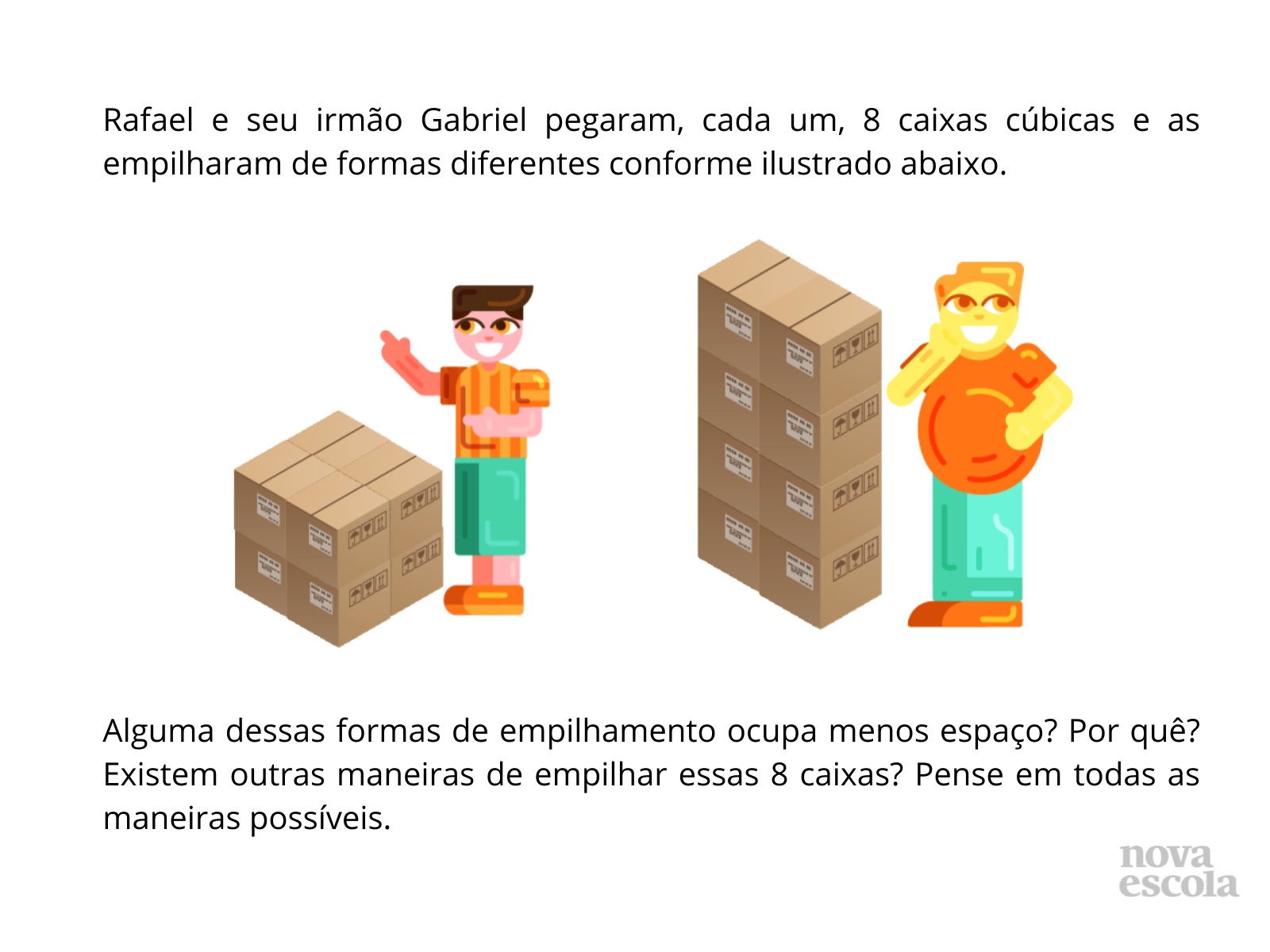
Tempo sugerido: 5 minutos.
Orientações: Utilize essa parte como um momento em que o aluno possa exercer sua autonomia podendo consolidar e avaliar o aprendido. Portanto, deixe que trabalhe individualmente essa atividade. O aluno precisa concluir que não importa a forma de empilhamento das caixas. Como a quantidade de caixas não será alterada, qualquer forma de empilhamento ocupará o mesmo espaço, consequentemente, o volume total não se altera. Utilize esse momento como forma de avaliar os alunos em termos de independência, formas diversas de pensar sobre o problema e alcance dos objetivos pretendidos na aula. Circule para verificar como os alunos estão pensando e registrando suas respostas. Você pode fazer o download desta atividade para imprimir para os seus alunos aqui.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante. Acesse a resolução dessa atividade.
Materiais complementares
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Código do plano MAT5_23GRM01
Recursos
- Necessários: -
- Opcionais: -
Para este plano, foque na etapa Aquecimento, Atividade principal e Discussão das soluções
Aquecimento
Professor(a), você pode realizar o Aquecimento deste plano com seus alunos, seja em uma aula síncrona ou assíncrona. Compartilhe com a turma o slide presente nesta atividade e solicite que tentem resolver o problema. Sugerimos que a imagem do slide ou o documento com a atividade seja disponibilizado, visto que possui uma diagramação que pode não ser contemplada em um texto corrido. Compartilhe, em formato de texto, os questionamentos presentes no “Discuta com a turma”. Caso a aula esteja ocorrendo de forma síncrona, permita que os alunos exponham suas resoluções e, caso esteja ocorrendo de forma assíncrona, os estudantes podem enviar suas considerações/reflexões em formato de texto ou áudio.
Atividade principal
Professor(a), compartilhe com a turma os slides presentes nesta atividade e solicite que tentem resolver o problema. Sugerimos que a imagem do slide ou o documento com a atividade seja disponibilizado, visto que possui uma diagramação que pode não ser contemplada em um texto corrido. Você pode encontrar o documento com a atividade aqui: https://nova-escola-producao.s3.amazonaws.com/P8q5Bzy9PEaGrdYZsGssxFTJERpw4B6HUMv796XMFxp6faDEp5H7dabuqCfW/ativprinc-mat5-23grm01.pdf. Compartilhe, em formato de texto, os questionamentos presentes no “Discuta com a turma”. Caso a aula esteja ocorrendo de forma síncrona permita que os alunos exponham suas resoluções e caso esteja ocorrendo de forma assíncrona os estudantes podem enviar suas considerações/reflexões em formato de texto ou áudio.
Discussão das soluções
Professor(a), compartilhe com a turma a resolução da atividade e utilize os questionamentos presentes no “Discuta com a turma” para fomentar a reflexão dos problemas de volume.
Sistematização e Encerramento
Professor(a), solicite que os alunos registrem em seus cadernos, a conclusão que chegam em relação ao volume. Questione se é possível objetos diferentes terem o mesmo volume. Caso considere viável, compartilhe com os estudantes os slides presentes nestas etapas do plano de aula. Compartilhe com os estudantes a construção do GeoGebra (https://www.geogebra.org/m/nDgxKMCC) e solicite que eles a explorem. A experimentação com o GeoGebra pode ajudar a entender o conceito de volume.
Raio X
O problema proposto no Raio X pode ser enviado em formato de imagem para os alunos e solicitado como uma “tarefa” a ser entregue em momento a ser combinado com a turma. Solicite que os alunos compartilhem suas resoluções através de imagens (fotos).
Convite às famílias
Professor(a), sugira que os alunos socializem com seus familiares o que aprenderam nesta aula sobre volume. Proponha que eles joguem “Cubos de Volume Matemático” com seus familiares, podendo encontrar o link a seguir: https://www.cokitos.pt/cubos-de-volume-matematico/play/.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alexandre Tolentino de Carvalho
Mentor: Fábio Menezes da Silva.
Especialista de área: Fernando Barnabé
Habilidade da BNCC
EF05MA21 - Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por meio de empilhamento de cubos, utilizando, preferencialmente, objetos concretos.
Objetivos específicos
- Reconhecer volume como espaço ocupado por um objeto podendo ser medido por meio de empilhamento de cubos
Conceito-chave
Medida de volume por meio de empilhamento de cubos
Recursos necessários
Lápis, borracha e caderno, objetos do cotidiano (caixas, embalagens, dados).