Plano de aula: Equações em ação: soluções em primeiro grau

Conversa inicial/Introdução

Tempo previsto: 20 min

Projete a tela do Simulador PhET “Explorador da igualdade” (https://phet.colorado.edu/sims/html/equality-explorer/latest/equality-explorer_all.html?locale=pt_BR) ou imprima os slides com os desenhos das balanças montadas no simulador. Usando a opção “Básico”, questione a turma a partir da imagem da Tela 1:

- A balança está equilibrada? O que isso significa?

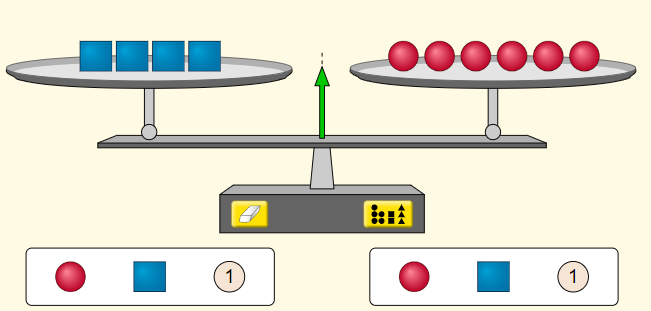
A ideia é que eles reconheçam que os quatro cubos pesam o mesmo que as seis esferas. Após ouvir as falas dos alunos, pergunte:

- O que acontecerá se eu adicionar 2 unidades em um dos lados da balança? E se eu fizer o mesmo do outro lado da balança?

Apresente a Tela 2 na simulação:

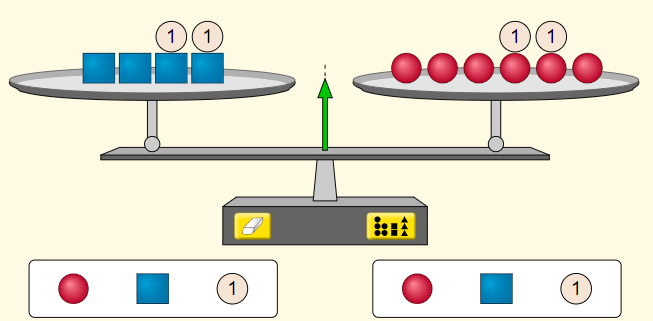
A ideia é que eles retomem que ao adicionar a mesma quantidade em ambos os membros de uma igualdade, a igualdade continuará verdadeira. Continue questionando:

- E se, agora, retirarmos uma unidade de cada lado da balança?

Então, deverão recordar que ao retirar a mesma quantidade de ambos os membros de uma igualdade, a mesma continuará verdadeira.

Retire mais uma unidade de cada lado e pergunte:

- O que acontecerá se dobrarmos a quantidade de peso em cada lado da balança? Ela vai continuar equilibrada?

Mostrando a situação da Tela 3, exemplifique a situação.

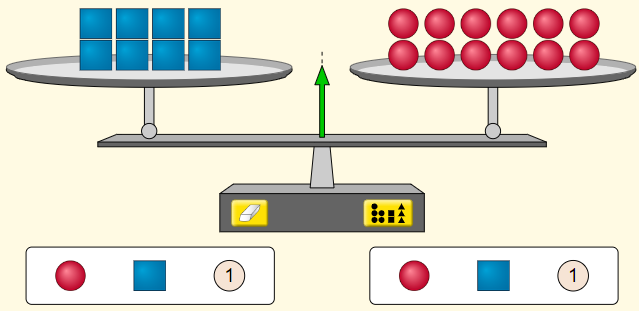
A ideia é retomar que ao multiplicar ambos os membros de uma igualdade por um mesmo número (neste caso o 2), ela continuará verdadeira.

Pergunte na sequência:

- Agora, o que vai acontecer se dividirmos a quantidade dos dois lados da balança por 4?

Aproveite para reforçar a utilização do símbolo de fração para representar a divisão por 4, escrevendo no quadro:

8 quadrados		12 esferas
	=
4		4

Ao realizar essas operações, apresente a Tela 4, na qual eles poderão verificar que a balança continua em equilíbrio, reforçando que ao dividir ambos os membros de uma igualdade por 4, ela continuará uma igualdade verdadeira.

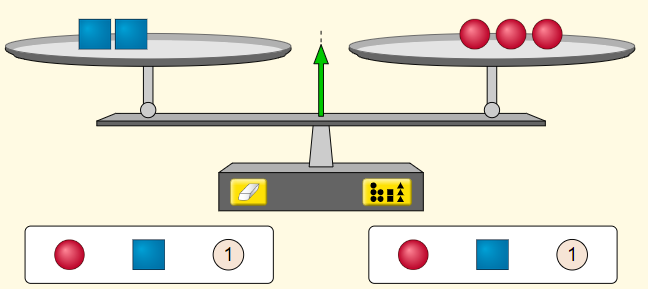
Agora, prepare a Tela 5 com antecedência, usando a aba “Variáveis” do simulador, para usar x = 2 e escrever a equação 3x + 1 = 7. Esconda o valor de x clicando no símbolo  ao lado.

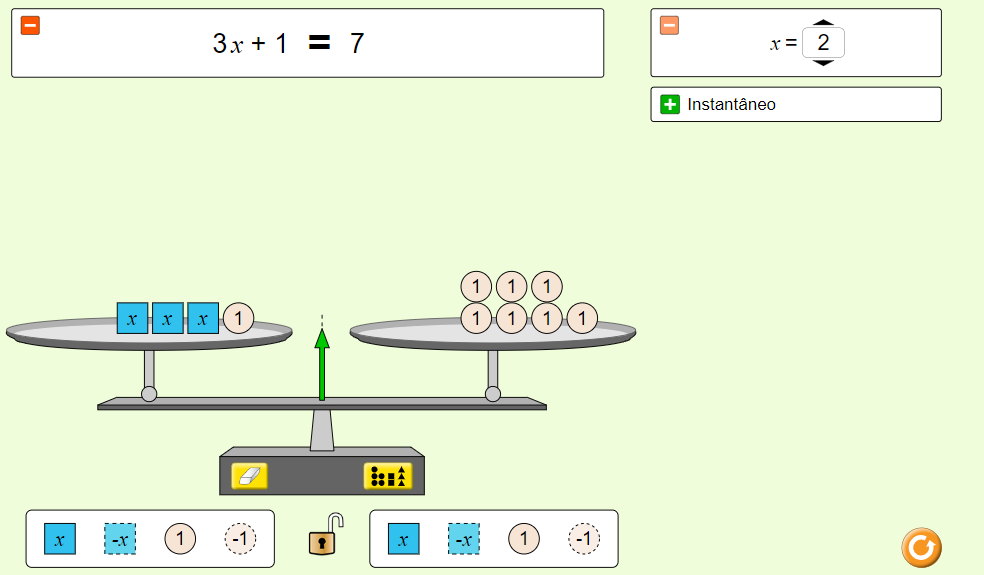
Ao apresentar a tela aos alunos, questione:

- Como podemos descobrir o valor do peso “x” se a balança está equilibrada?

Neste momento não é fundamental que todos consigam sugerir a utilização das propriedades da igualdade para resolver a equação. Se alguém fornecer essa proposta, deixe que verbalize para a turma e até manipule a simulação com sua ideia. Pode ser que descubram mentalmente o número que multiplicado por 3 e adicionado a 1 resulta em 7. O mais importante é reforçar com eles que essa situação pode ser representada por uma equação de primeiro grau com uma incógnita (valor desconhecido), colocando a igualdade na lousa e reforçando que ela é formada por uma igualdade que contém uma letra, números e operações e que encontrar a solução da equação é descobrir qual o valor que, quando colocado no lugar da letra “x”, torna a igualdade verdadeira.