Guia de Intervenção
Plano de Aula
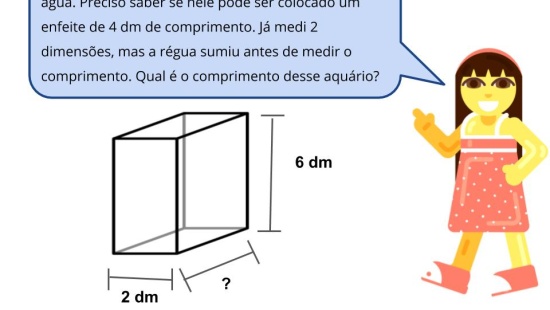
Plano de aula: Volume em 3D
Plano 2 de uma sequência de 5 planos. Veja todos os planos sobre Medição do volume de cubo e paralelepípedo
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Alexandre Tolentino de Carvalho
Mentor: Fábio Menezes da Silva.
Especialista de área: Fernando Barnabé
Habilidade da BNCC
EF05MA21 - Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por meio de empilhamento de cubos, utilizando, preferencialmente, objetos concretos.
Objetivos específicos
- Relacionar empilhamento de cubos à medida de volume dada em metros cúbicos, decímetros cúbicos ou centímetros cúbicos.
Conceito-chave
Volume de sólidos geométricos.
Recursos necessários
- Lápis,
- Borracha,
- Caderno,
- Régua,
- Dados,
- Caixas cúbicas
Habilidades BNCC:
Objetivos de aprendizagem
- Relacionar empilhamento de cubos à medida de volume dada em metros cúbicos, decímetros cúbicos ou centímetros cúbicos.

Precisa de ajuda para criar uma aula personalizada?
Crie seu plano de aula em menos de um minuto no WhatsApp.