Título: Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Tempo sugerido: 6 minutos (Slides 3 à 5).
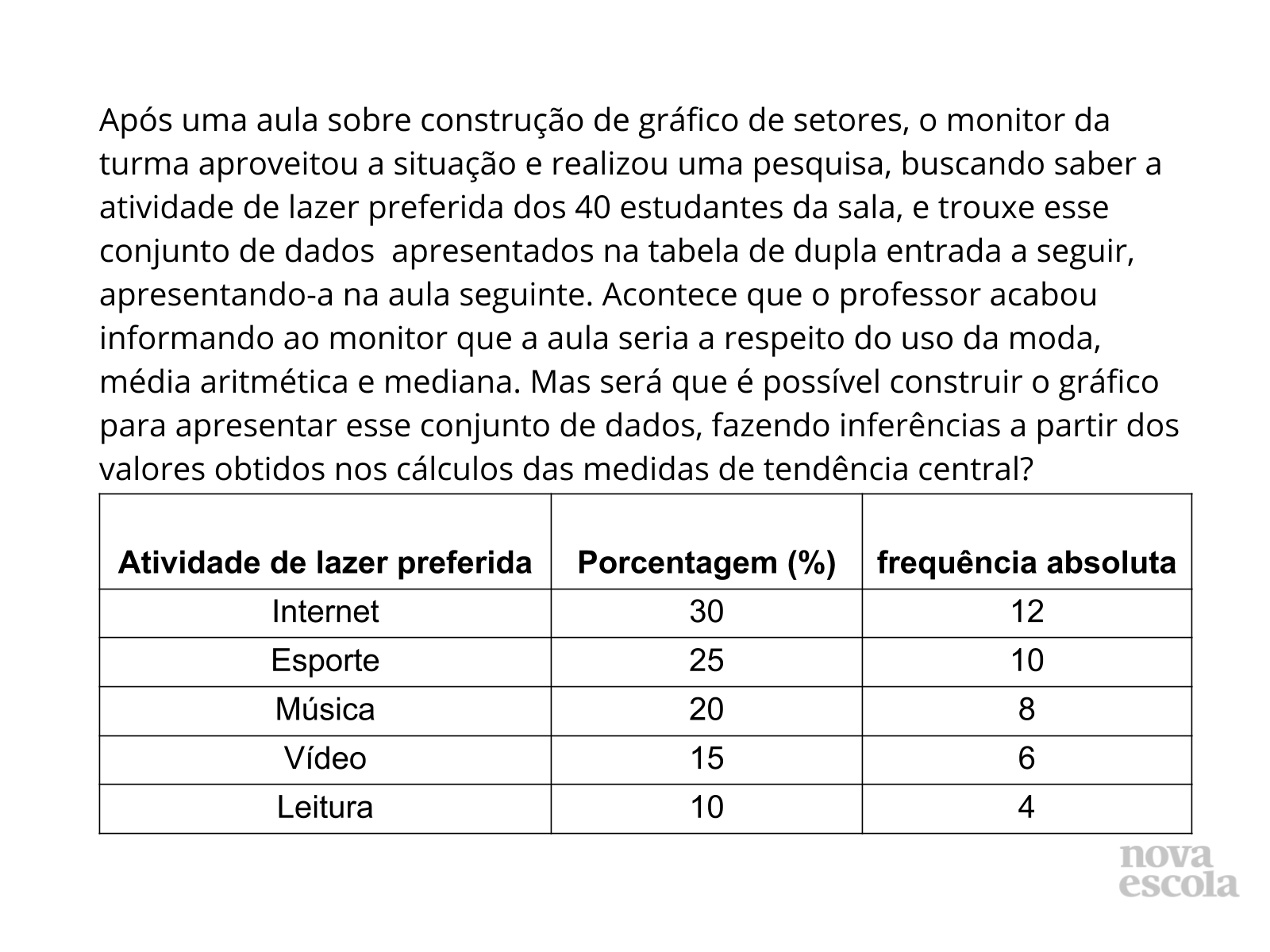
Orientações: Inicie a aula perguntando, para relembrar aos alunos, se eles conhecem algumas medidas de tendência central (moda, mediana e média aritmética). Anote as respostas deles no quadro e peça que eles falem um pouco sobre cada uma. Agora leia junto com eles o problema e faça-os refletir na possível solução.
A Planilha eletrônica geradora dessa tabela pode ser acessada em “Materiais Complementares”.
Propósito: Relembrar, a partir da fala dos alunos, quais são as medidas de tendência central conhecidas por eles e o que significam os valores obtidos a partir do cálculo de cada uma delas, considerando, através do problema e de sua solução, a retomada do assunto.
Discuta com a turma:
- As variáveis são qualitativas ou quantitativas?
- Nessa situação, faz sentido usarmos a moda, a mediana e média? Chegaríamos a alguma conclusão?
Retomada
Tempo sugerido: 6 minutos (Slides 3 à 5).
Orientações: Inicie a aula perguntando, para relembrar aos alunos, se eles conhecem algumas medidas de tendência central (moda, mediana e média aritmética). Anote as respostas deles no quadro e peça que eles falem um pouco sobre cada uma. Agora leia junto com eles o problema e faça-os refletir na possível solução.
Propósito: Relembrar, a partir da fala dos alunos, quais são as medidas de tendência central conhecidas por eles e o que significam os valores obtidos a partir do cálculo de cada uma delas, considerando, através do problema e de sua solução, a retomada do assunto.
Discuta com a turma:
- As variáveis são qualitativas ou quantitativas?
- Nessa situação, faz sentido usarmos a moda, a mediana e média? Chegaríamos a alguma conclusão?
Retomada
Tempo sugerido: 6 minutos (Slides 3 à 5).
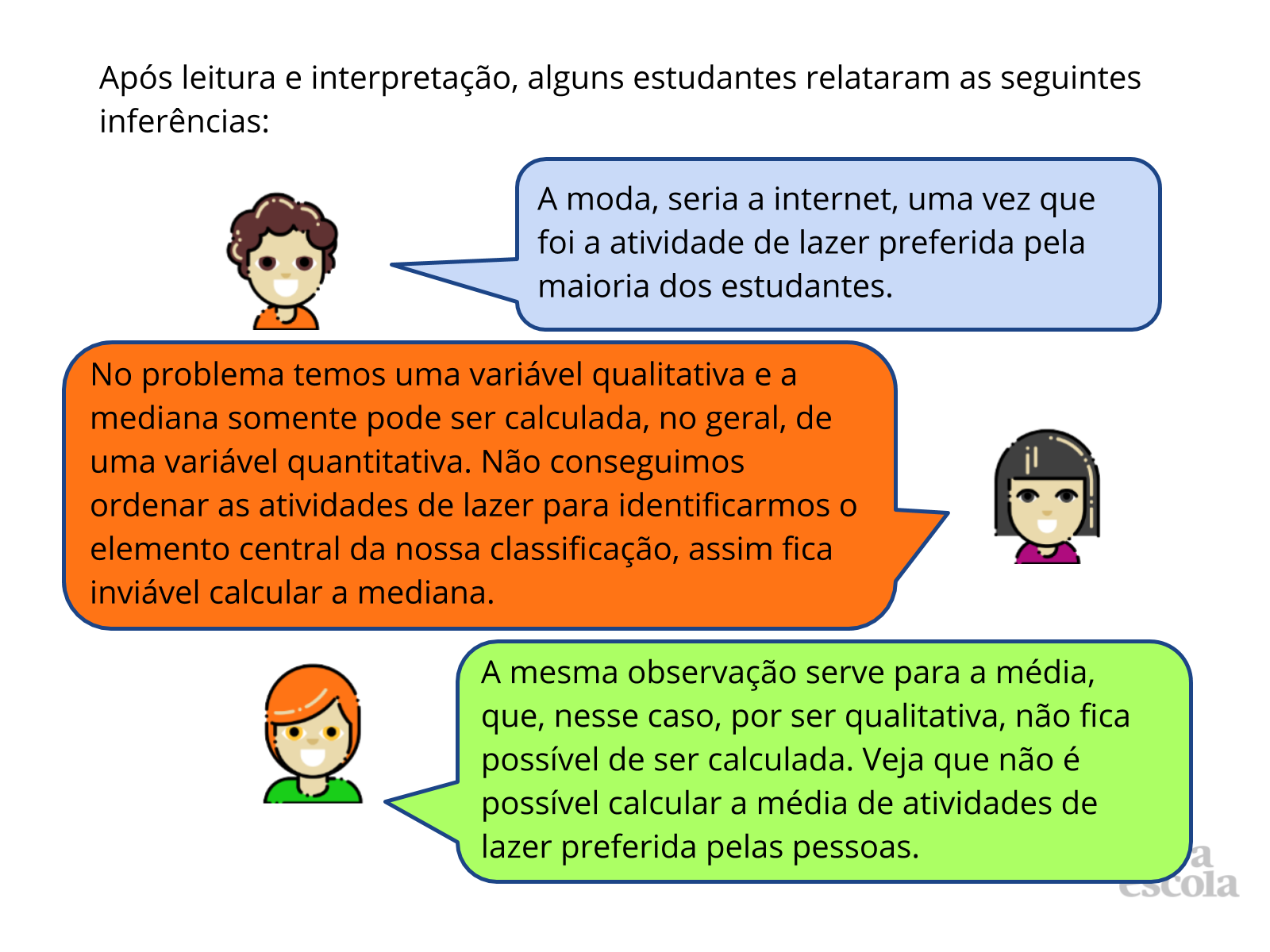
Orientações: Inicie a aula perguntando, para relembrar aos alunos, se eles conhecem algumas medidas de tendência central (moda, mediana e média aritmética). Anote as respostas deles no quadro e peça que eles falem um pouco sobre cada uma. Agora leia junto com eles o problema e faça-os refletir na possível solução.
Propósito: Relembrar, a partir da fala dos alunos, quais são as medidas de tendência central conhecidas por eles e o que significam os valores obtidos a partir do cálculo de cada uma delas, considerando, através do problema e de sua solução, a retomada do assunto.
Discuta com a turma:
- As variáveis são qualitativas ou quantitativas?
- Nessa situação, faz sentido usarmos a moda, a mediana e média? Chegaríamos a alguma conclusão?
Atividade principal

Tempo sugerido: 20 minutos.
Orientações: Peça que os alunos leiam a atividade, analisem a tabela e pensem em formas de resolver a atividade.
Propósito: Fazer com que os alunos pensem nas medidas de tendência central de acordo com a tabela.
Discuta com a turma:
- Olhando apenas para os dados apresentados na tabela, é possível obter a moda? Como?
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Discussão de soluções
Tempo sugerido: 15 minutos (Slides 7 e 8).
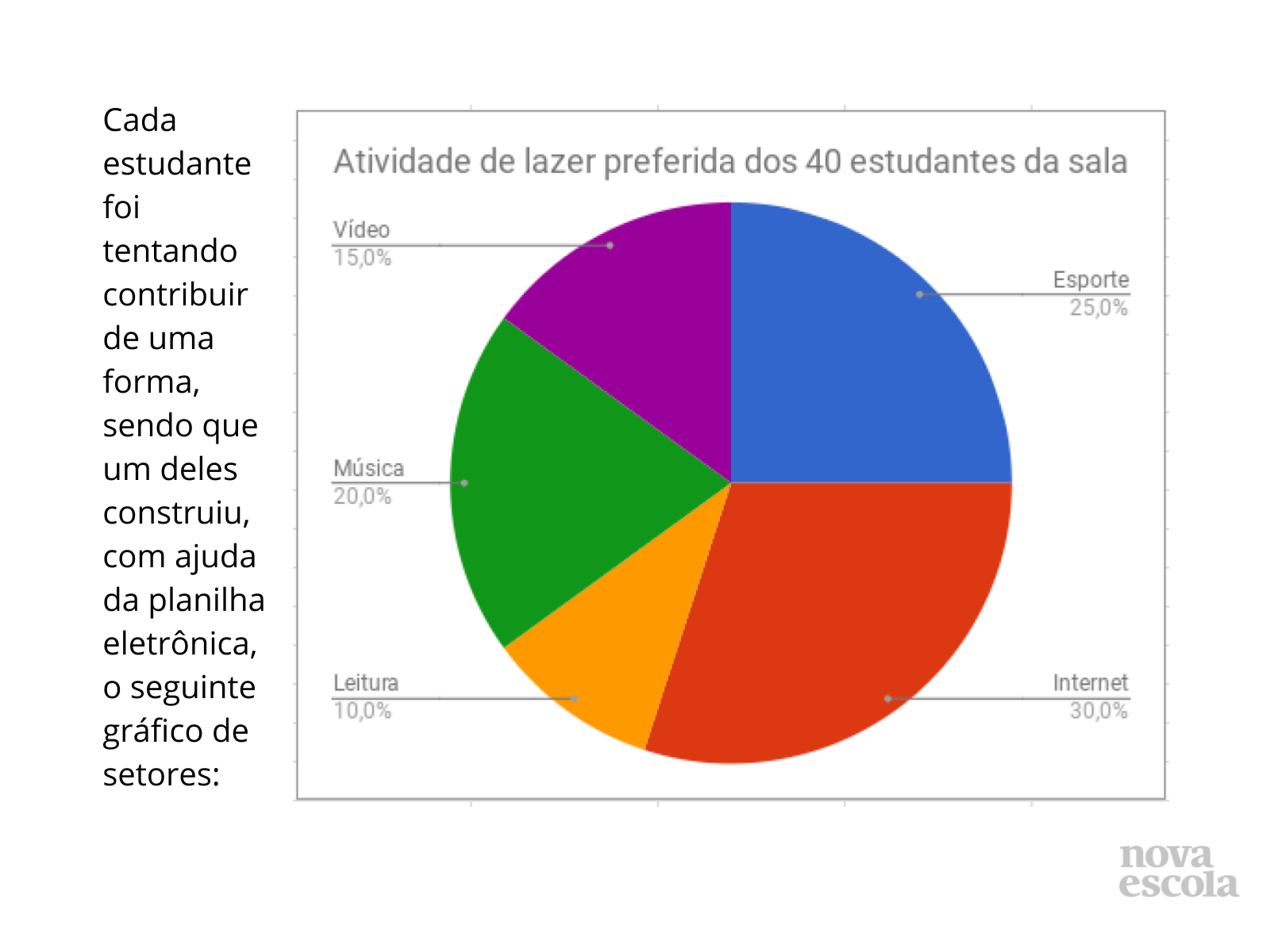
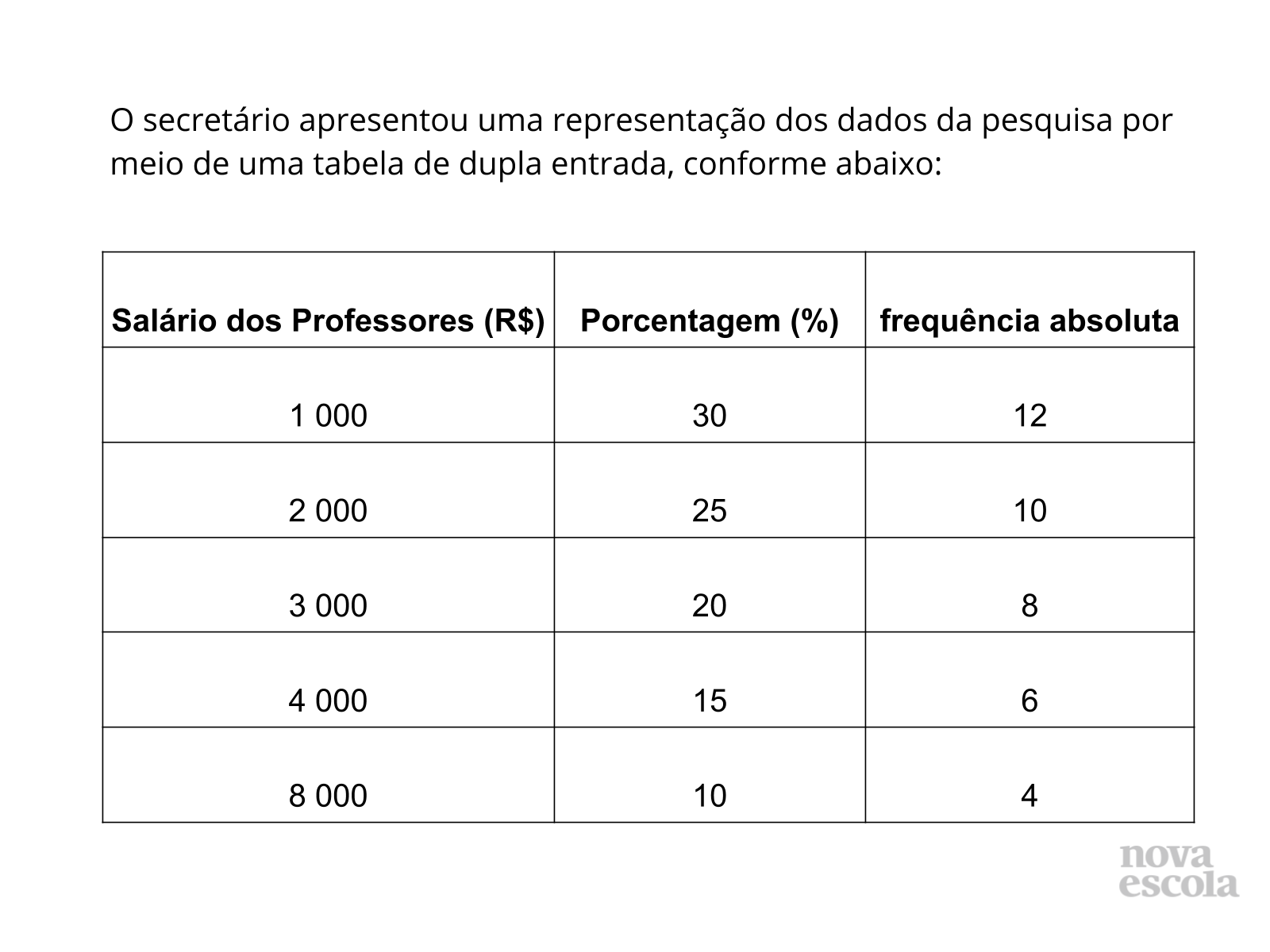
Orientações: Peça que os alunos interpretem bem a nova tabela, de dupla entrada, gerada pelo gráfico de setores por um tempo.
Propósito: Fazer com que os alunos pensem nas medidas de tendência central de acordo com a nova tabela, de dupla entrada, gerada pelo gráfico de setores.
Discuta com a turma:
- Olhando apenas para os dados apresentados tabela de dupla entrada, gerada pelo gráfico de setores, agora sim, é possível obter a média mais facilmente? E a mediana? Como?
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Discussão de soluções
Tempo sugerido: 15 minutos (Slides 7 e 8).
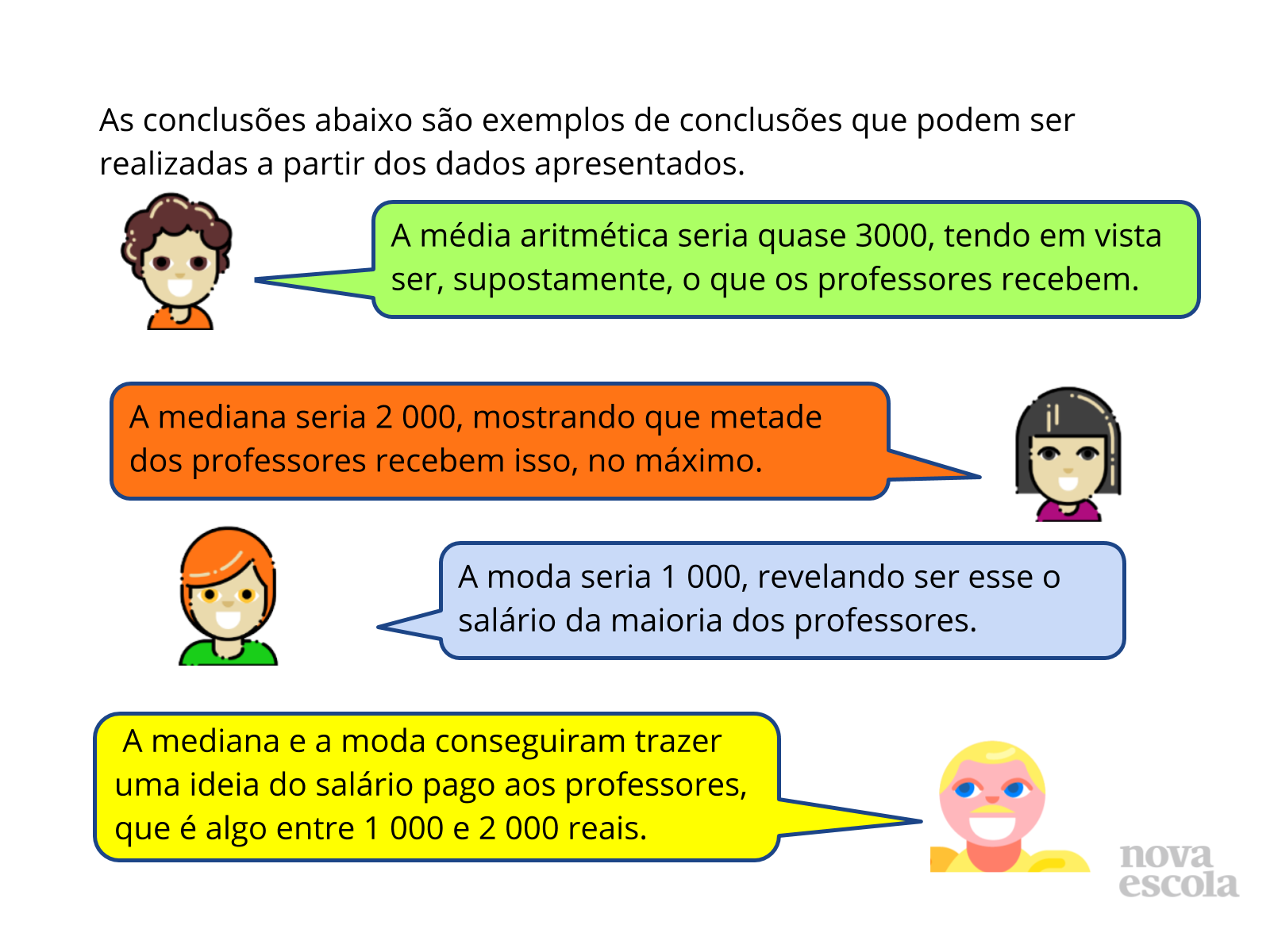
Orientações: Peça que os alunos comparem as inferências da forma que foram colocadas e peça que as comparem com as realizadas em sala. Utilize o guia de intervenção se julgar ser necessário.
Propósito: Fazer com que os alunos repensem nas inferências relatadas, à partir das medidas de tendência central de acordo com o gráfico de setores.
Discuta com a turma:
- Existem outras inferências que poderiam ser citadas?
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.
Encerramento

Tempo sugerido: 2 minutos.
Orientações: Encerre a atividade lembrando de mencionar novamente que, independentemente de como o conjunto de dados seja apresentado, até mesmo em gráficos de setores, ao se analisar criticamente esses dados, utilizando medidas de tendência central, é possível se chegar a conclusões e tomar decisões para um determinado problema.
Raio X
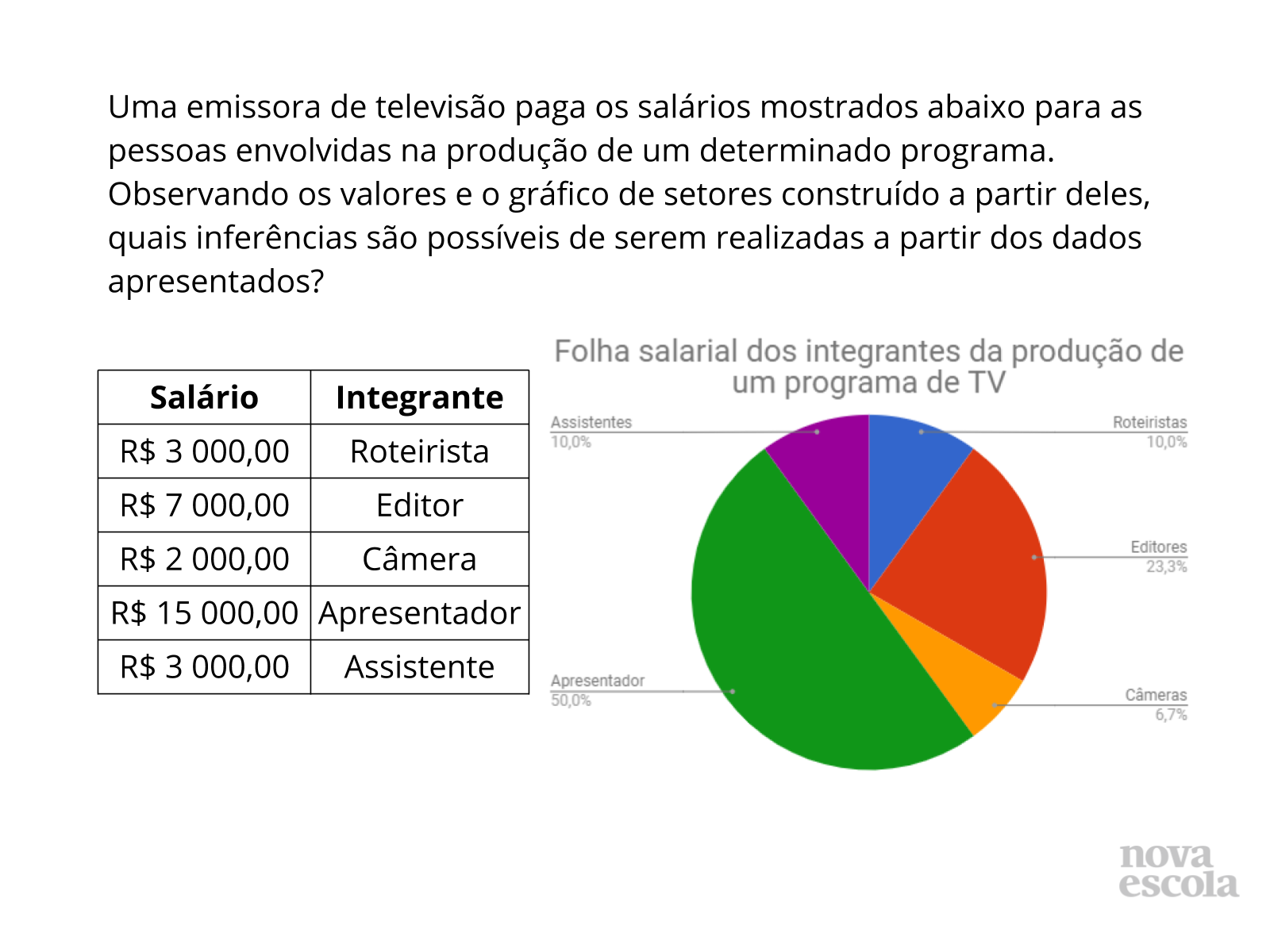
Tempo sugerido: 5 minutos.
Orientações: Peça que, individualmente, os alunos leiam a atividade e a realizem. Circule para verificar como os alunos estão realizando o raio x, pois é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar se ainda há alguma dificuldade em cada um. Por fim, ordene os valores em ordem crescente (também pode ser decrescente), verifique a moda e a mediana, para só depois calcular a média aritmética.
Propósito: Verificar se os alunos aplicam os conhecimentos adquiridos numa situação semelhante e avaliar os conhecimentos de cada um.
Você encontra essa atividade e sua resolução para impressão na aba “Materiais Complementares” desse plano.