Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Aquecimento

Tempo sugerido: 5 minutos
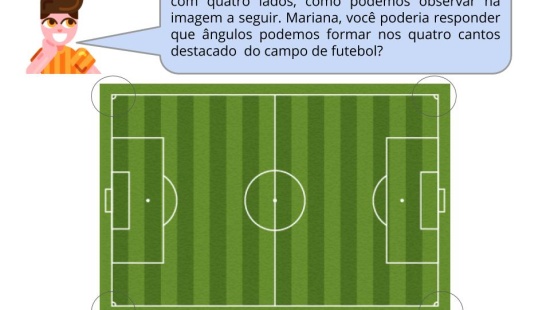
Orientação: Projete a atividade ou escreva na lousa para que todos leiam com atenção. Peça para os alunos responderem as questões propostas por escrito dando um tempo para eles. Em seguida peça para cada uma na sua vez ler a resposta obtida. Vá comparando os resultados falados pelos alunos e, caso necessário, registre na lousa os resultados. Verifique se algum aluno não soube ler a horário adequadamente. Se necessário faça a leitura coletiva dos minutos usando a base 5 para contagem (0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 minutos). Em último caso faça a leitura das horas. Explique que o ponteiro menor indica as horas e que o ponteiro maior os minutos.
Faça o desenho do relógio com o horário 10h00 e peça para os alunos compararem a abertura entre os dois horários. Espera-se que com esta atividade o aluno verifique que a abertura dos ponteiros às 10h00 é menor que a abertura às 9h00.
Propósito: Inserir o aluno na aula e explorar os ângulos formados entre os ponteiros de um relógio analógico.
Discuta com a turma:
- O quê o ponteiro menor do relógio indica? E o ponteiro maior?
- Se o ponteiro maior está no 4 isto significa o quê? Como você chegou a este resultado?
- A medida do ângulo está relacionada ao tamanho dos ponteiros ou à outra coisa? O que estaria relacionada à medida do ângulo?
Atividade Principal

Tempo sugerido: 15 minutos
Orientação: Inicialmente organize a sala em duplas produtivas. Distribua cópias impressas para cada aluno realizar a atividade. Faça a leitura compartilhada das ações envolvidas na Atividade. Verifique se há alguma dúvida em relação ao enunciado e dê alguns minutos para os aluno resolverem. Caminhe pela sala de aula observando as interações entre os alunos. Verifique se o aluno identificou corretamente os horários e reconhece a diferença entre o que é indicado pelo ponteiro menor e aquilo que é indicado pelo ponteiro maior no relógio. Assim que encerrada a resolução solicite que os alunos compartilhem um com o outro seus resultados.
Propósito: Explorar os ângulos formados pelos ponteiros do relógio a fim de classificá-los em retos, agudos ou obtusos.
Discuta com a turma:
- Se um ponteiro der meia volta no mostrador do relógio quantos graus você acha que ele se moveu? E se fosse apenas ¼ da volta?
- Quando o ponteiro maior (minutos) se move o que ocorre com o ponteiro menor (horas)?
- Existe algum horário onde não haveria abertura entre os ponteiros? Que horário é este?
- Você conhece algum horário onde os ponteiros estão em direções opostas? Qual horário seria?
Materiais para Impressão:
Atividade Principal
Resolução da Atividade Principal
Guia de Intervenção
Discussão de soluções (Slides 5 e 6)
Tempo sugerido: 15 minutos.
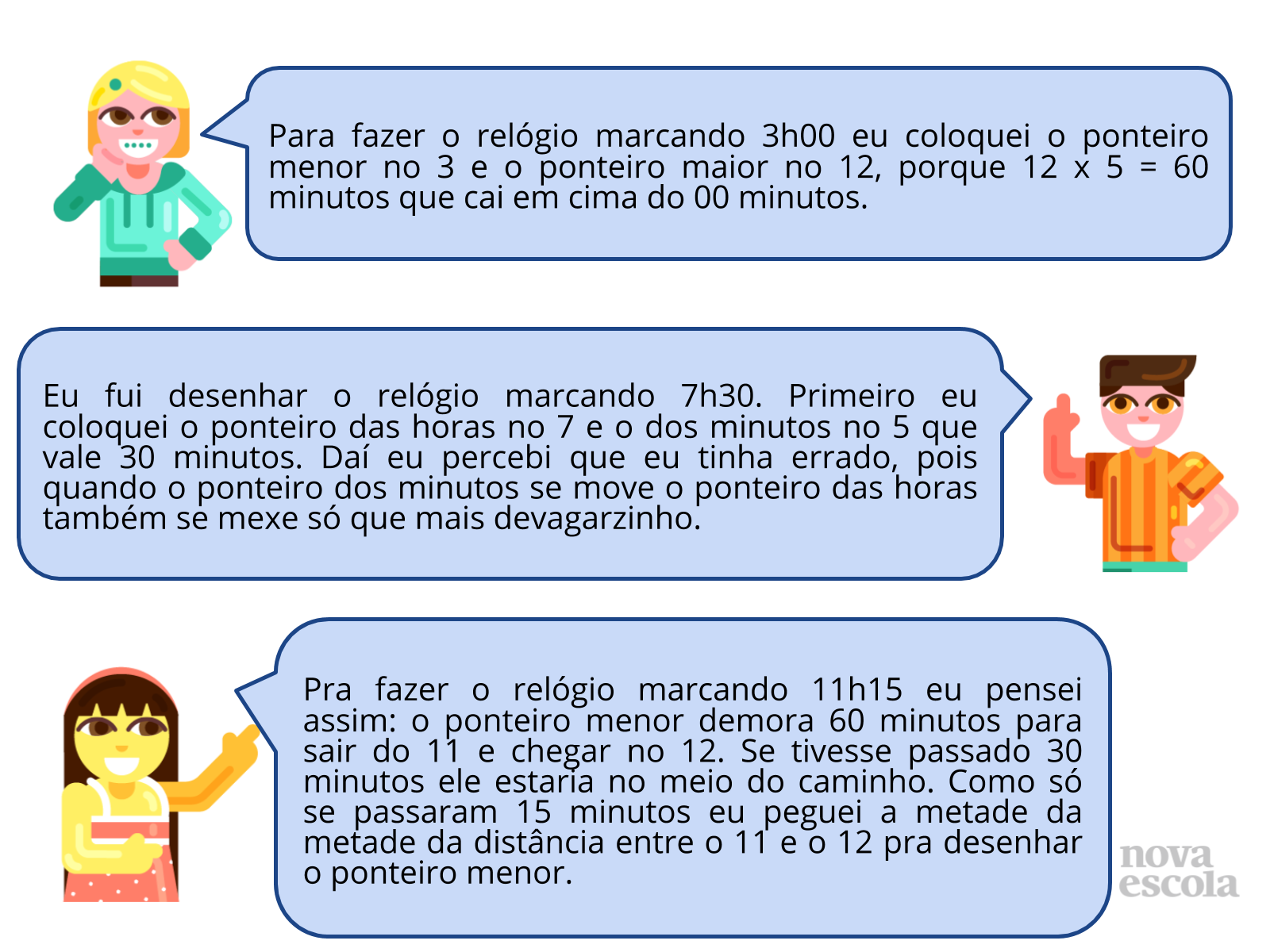
Orientações: Inicialmente verifique se os desenho dos ponteiros coincidiu. É provável que muitos alunos se confundam com os horários 7h30 e 11h15. Isto ocorre pois os alunos não reconhecem que à medida que o ponteiro maior (minutos) se movimenta o ponteiro menor (horas) também se desloca, porém com uma velocidade menor. Por isto é provável que alguns alunos indiquem 7h30 com o ponteiro menor no 7 e o ponteiro maior no 6 (30 minutos) o que é incorreto. O mesmo vale para o horário das 11h15 onde alguns alunos podem indicar o ponteiro menor no 11 e o ponteiro maior no 3 (15 minutos), o que também é incorreto.
Verificada as posições corretas dos ponteiros é necessário fazer a comparação com o ângulo reto (3h00). Para isto o aluno deverá verificar que o ponteiro menor percorreu ¼ do mostrador. Logo 360º : 4 = 90º. É através da comparação da abertura deste ângulo que os alunos irão classificar os demais (7h30 será um ângulo agudo pois a abertura é menor que 90º e 11h15 será um ângulo obtuso pois a abertura é maior que 90º).
Propósito: Comparar as hipóteses levantadas pelos alunos durante a Atividade Principal. Correlacionar os ângulos formados pelos ponteiros do relógio com a classificação dos ângulos.
Discuta com a turma:
- Começando de 0h00 até 1h00 haveria algun(s) horário(s) onde teríamos um ângulo reto? Qual(is) horário(s) seria(m) este(s)?
- Neste mesmo intervalo de tempo existe algum horário onde teríamos os ângulos formados entre os ponteiros seriam agudos? Entre quais horários isto ocorreria?
- E haveria neste intervalo de tempo um horário onde o ângulo formado pelos ponteiros seria obtuso? Dê um exemplo neste caso.
Discussão de soluções (Slides 5 e 6)

Tempo sugerido: 15 minutos.
Orientações: Inicialmente verifique se os desenho dos ponteiros coincidiu. É provável que muitos alunos se confundam com os horários 7h30 e 11h15. Isto ocorre pois os alunos não reconhecem que à medida que o ponteiro maior (minutos) se movimenta o ponteiro menor (horas) também se desloca, porém com uma velocidade menor. Por isto é provável que alguns alunos indiquem 7h30 com o ponteiro menor no 7 e o ponteiro maior no 6 (30 minutos) o que é incorreto. O mesmo vale para o horário das 11h15 onde alguns alunos podem indicar o ponteiro menor no 11 e o ponteiro maior no 3 (15 minutos), o que também é incorreto.
Verificada as posições corretas dos ponteiros é necessário fazer a comparação com o ângulo reto (3h00). Para isto o aluno deverá verificar que o ponteiro menor percorreu ¼ do mostrador. Logo 360º : 4 = 90º. É através da comparação da abertura deste ângulo que os alunos irão classificar os demais (7h30 será um ângulo agudo pois a abertura é menor que 90º e 11h15 será um ângulo obtuso pois a abertura é maior que 90º).
Propósito: Comparar as hipóteses levantadas pelos alunos durante a Atividade Principal. Correlacionar os ângulos formados pelos ponteiros do relógio com a classificação dos ângulos.
Discuta com a turma:
- Começando de 0h00 até 1h00 haveria algun(s) horário(s) onde teríamos um ângulo reto? Qual(is) horário(s) seria(m) este(s)?
- Neste mesmo intervalo de tempo existe algum horário onde teríamos os ângulos formados entre os ponteiros seriam agudos? Entre quais horários isto ocorreria?
- E haveria neste intervalo de tempo um horário onde o ângulo formado pelos ponteiros seria obtuso? Dê um exemplo neste caso.
Sistematização do conceito

Tempo sugerido: 5 minutos
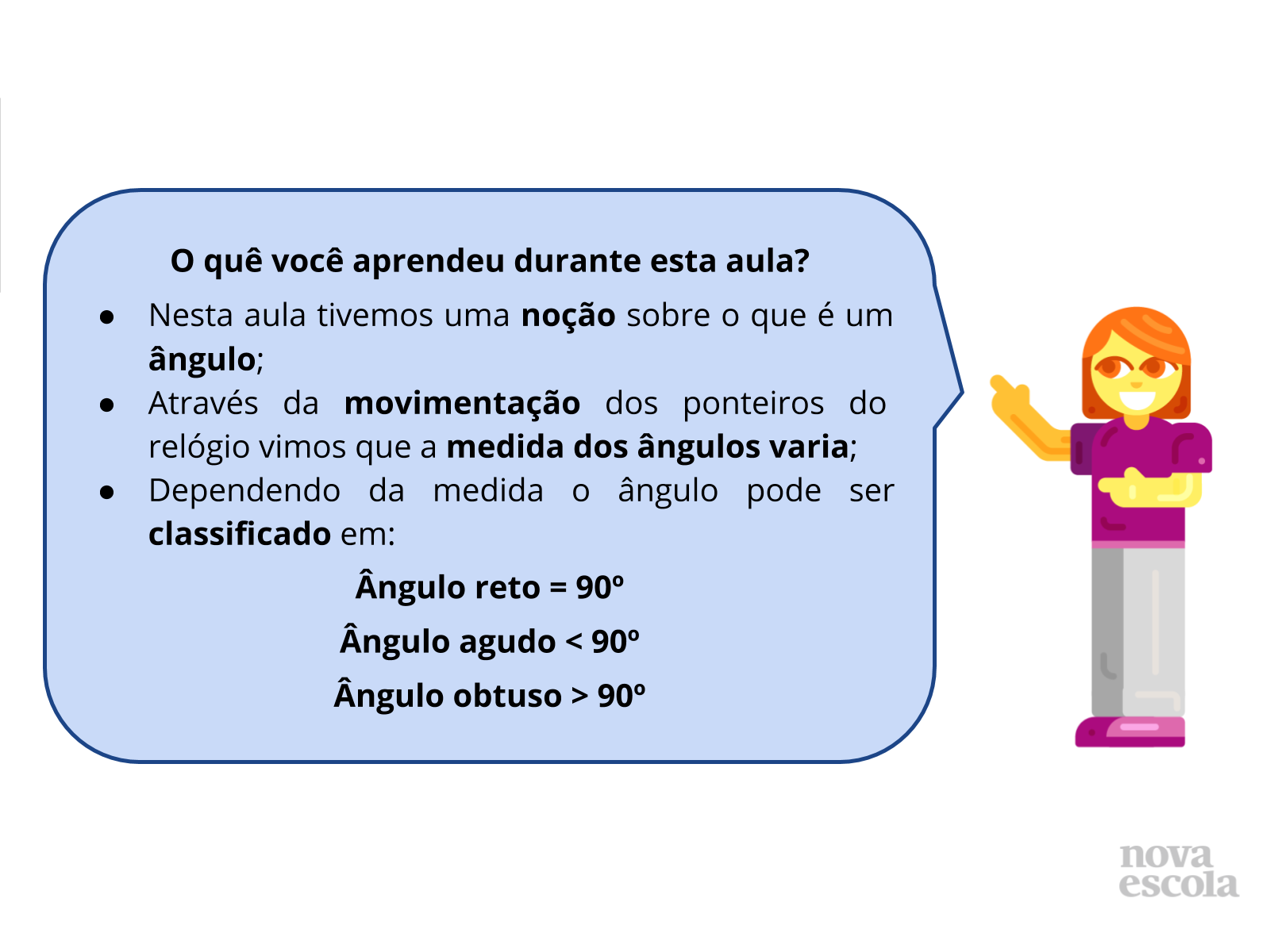
Orientação: Projete o slide ou escreva na lousa os principais momentos da aula associando aos conceitos matemáticos envolvidos. Você irá refinar os conceitos desenvolvidos ao longo da aula dando o enfoque matemático necessário. Fique atento às definições de ângulo como sendo uma região plana formada por duas semirretas de mesma origem. Quando for se referir à classificação dos ângulos sempre use a palavra medida do ângulo.
Propósito: Compreender a classificação dos ângulos.
Encerramento
Tempo sugerido: 3 minutos
Orientação: Neste momento faremos o fechamento da aula elencando os principais resultados obtidos durante a aula. Sempre que o aluno sentir necessidade ele poderá usar esta informação. No caso as informações pertinentes desta aula são a noção de ângulo e sua classificação de acordo com a medida.
Propósito: Sintetizar os principais resultados desenvolvidos nesta aula.
Raio X

Tempo sugerido: 5 minutos
Orientação: Entregue uma folha impressa para cada aluno desenhar os ângulos solicitados. Peça para eles classificarem os ângulos de acordo com a abertura dos ponteiros do relógio. Não há necessidade de uso do transferidor. Peça apenas que o aluno analise a abertura formada pelos ponteiros e a compare com o ângulo de referência (ângulo reto).
Propósito: Verificar se o objetivo da aula foi atingido (associar os giros às representações dos ângulos).
Discuta com a turma:
- Qual seria a definição formal de ângulo reto? E de ângulo agudo? E do ângulo obtuso?
- Existem outros tipos de ângulos que poderíamos usar na classificação?
- O que seria um ângulo nulo? E um ângulo de meia-volta?
Materiais para Impressão:
Atividade Complementar
Atividade Raio X
Resolução da Atividade Complementar
Resolução da Atividade Raio X