Atividade principal
Plano de Aula
Plano de aula: Isso faz sentido! Multiplicação de números inteiros
Plano 8 de uma sequência de 10 planos. Veja todos os planos sobre Operações com números inteiros
Descrição
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Danilo Pires de Azevedo
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF07MA04) Resolver e elaborar problemas que envolvam operações com números inteiros.
Objetivos específicos
- Representar na reta numerada segmentos de reta quando multiplicados por um número negativo ou positivo.
- Resolver situações-problema envolvendo números inteiros.
- Utilizar a operação básica de multiplicação envolvendo números inteiros de forma adequada.
Conceito-chave
Multiplicação de números inteiros; modificações na reta numerada a partir de multiplicações; sentido e relação com números inteiros.
Recursos necessários
Lápis, borracha e régua. Se possível, papel quadriculado.
Habilidades BNCC:
Objetivos de aprendizagem
- Representar na reta numerada segmentos de reta quando multiplicados por um número negativo ou positivo.
- Resolver situações-problema envolvendo números inteiros.
- Utilizar a operação básica de multiplicação envolvendo números inteiros de forma adequada.
Resumo da aula
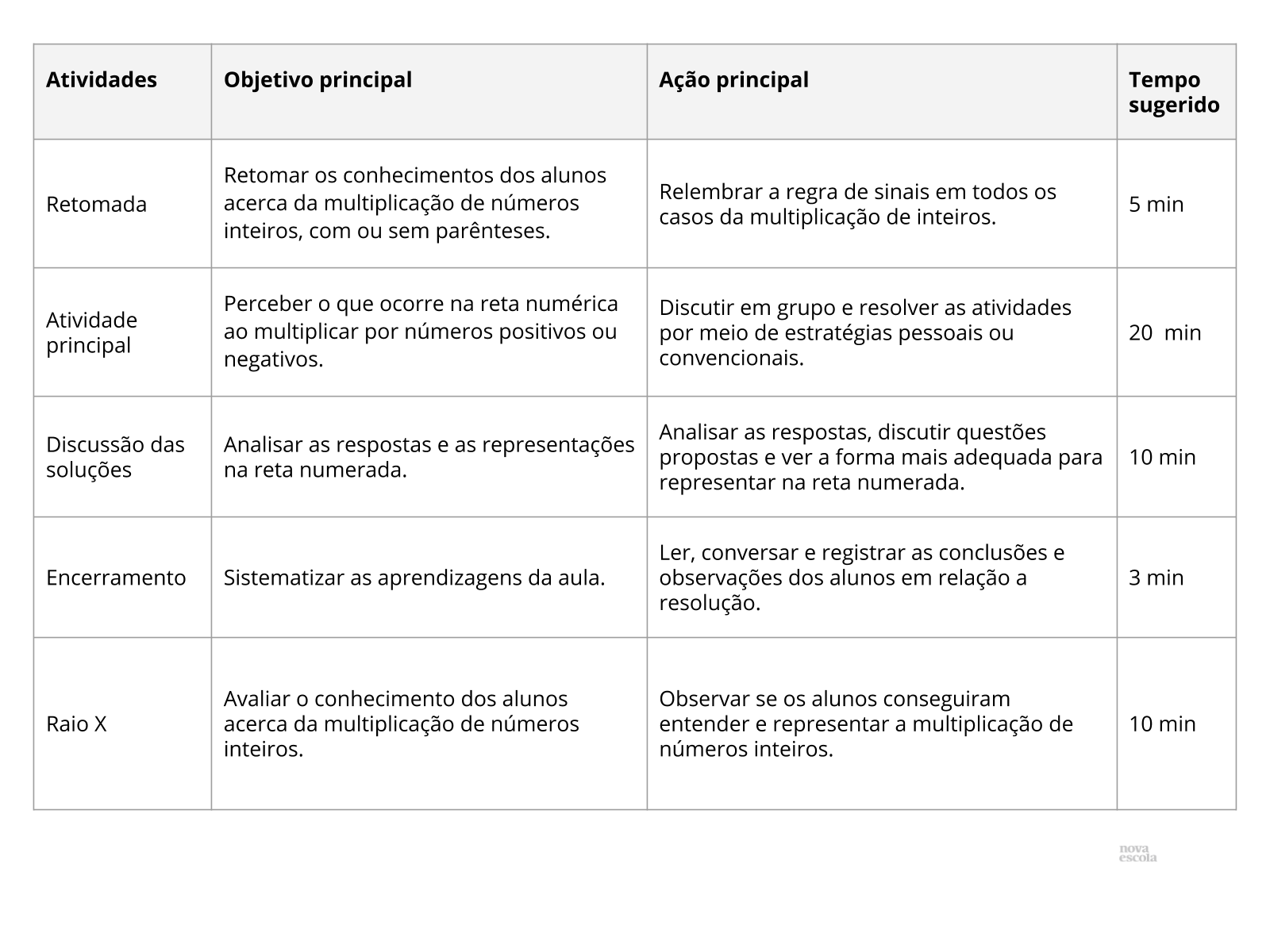 Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula. Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos.
Orientações: Projete ou leia o objetivo para a turma. O objetivo dessa aula é fazer com que os alunos consigam relacionar de maneira eficaz a multiplicação de números inteiros, por meio de estratégias pessoais ou convencionais.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 5 minutos
Orientação: Anote no quadro essas multiplicações. Converse com os alunos sobre a resolução de cada uma delas e ouça as sugestões dos mesmos. Utilizar os mesmos números, faz com que eles percebam que o que se altera serão os sinais:
4 x (-5) = -20
(-4) x (-5) = +20
(-4) x 5 = -20
(+4) x (+5) = +20
Se necessário for, relembre os alunos que sinais iguais resulta em um produto positivo e sinais diferentes em um negativo. Evite falas como: “Menos com menos dá mais”, “Mais com menos dá menos”, etc. Isso causa grande confusão com os alunos ao trabalharem com soma e subtração, após terem trabalhado multiplicação e divisão.
Propósito: Relembrar a multiplicação de números inteiros.
Discuta com a turma:
- Os parênteses são importantes?
- E se eu colocasse mais um número, por exemplo: (-4) x (+5) x (-2), qual seria o sinal do resultado?
- Há diferentes estratégias de resolução?
Atividade Principal
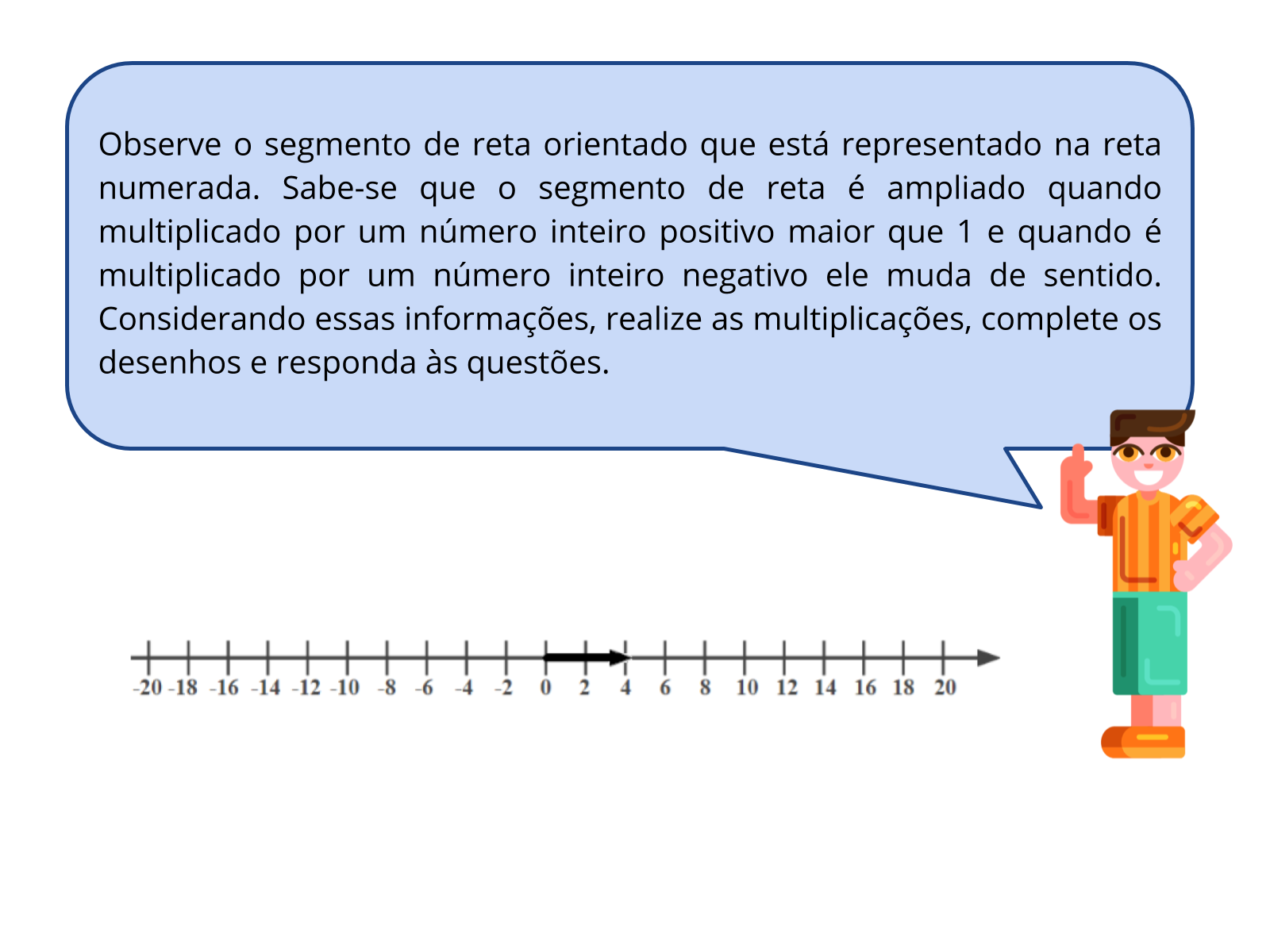
Tempo sugerido: 20 minutos (Slides 4 a 8)
Orientação:
- Você pode projetar, imprimir ou construir as retas numeradas na lousa. A utilização de papel quadriculado também pode auxiliar para a construção das retas.
- Organize os alunos em duplas ou trios e solicite que leiam os enunciados com muita atenção. Caminhe pela sala e veja se estão conseguindo representar adequadamente os segmentos na reta numerada com o sentido correto. Assim, poderá relacionar a mudança de sentido com a mudança de sinal quando a multiplicação ocorre por um número negativo.
- Evite falas como: “Menos com menos dá mais”, “Mais com menos dá menos”, etc. Isso causa grande confusão com os alunos ao trabalharem com soma e subtração, após terem trabalhado multiplicação e divisão.
Propósito: Fazer com que os alunos relacionem a mudança de sentido na reta numerada com o resultado das multiplicações.
Materiais Complementares:
Atividade Principal
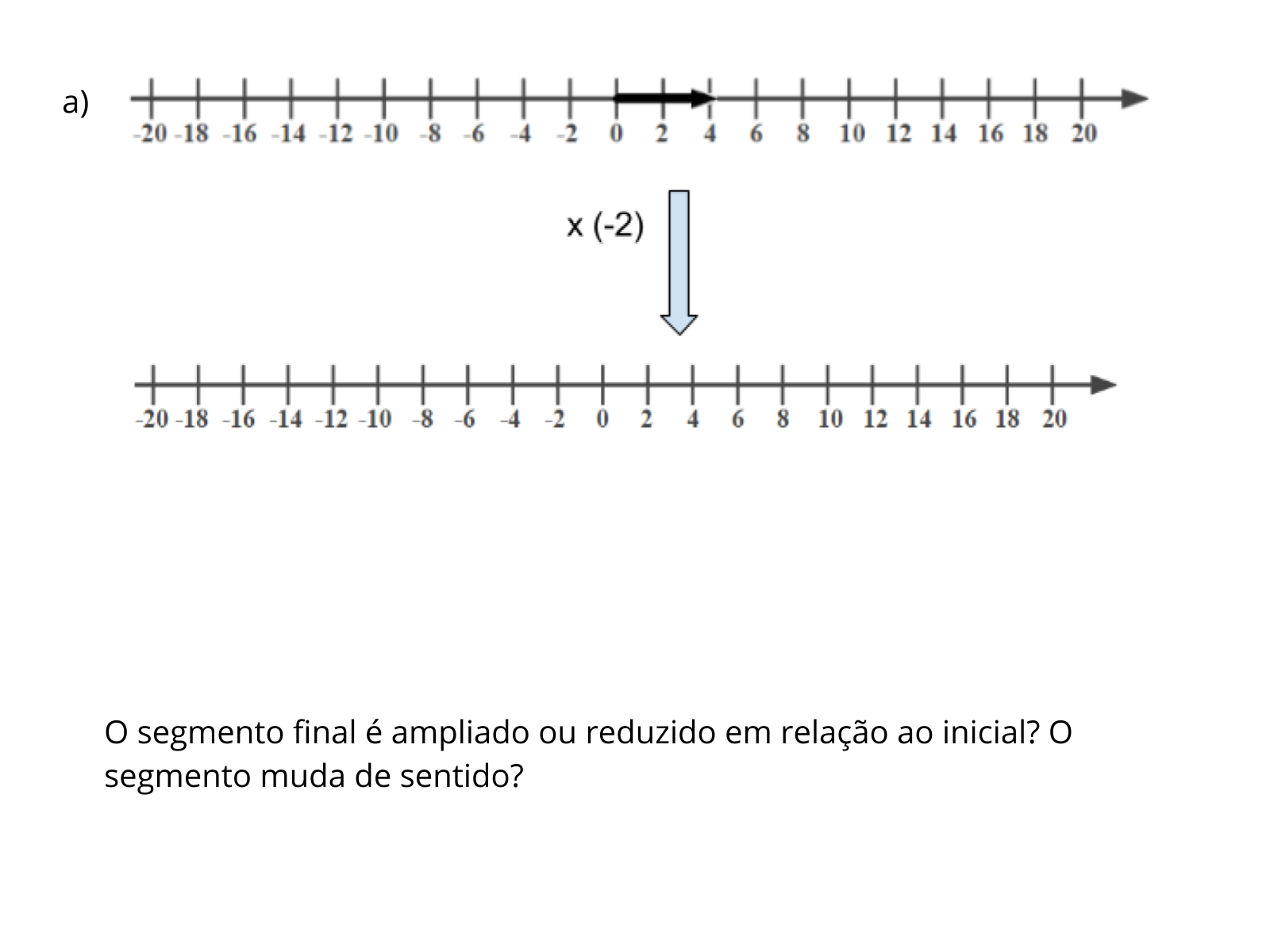
Tempo sugerido: 20 minutos (Slides 4 a 8)
Orientação:
- Você pode projetar, imprimir ou construir as retas numeradas na lousa. A utilização de papel quadriculado também pode auxiliar para a construção das retas.
- Organize os alunos em duplas ou trios e solicite que leiam os enunciados com muita atenção. Caminhe pela sala e veja se estão conseguindo representar adequadamente os segmentos na reta numerada com o sentido correto. Assim, poderá relacionar a mudança de sentido com a mudança de sinal quando a multiplicação ocorre por um número negativo.
- Evite falas como: “Menos com menos dá mais”, “Mais com menos dá menos”, etc. Isso causa grande confusão com os alunos ao trabalharem com soma e subtração, após terem trabalhado multiplicação e divisão.
Propósito: Fazer com que os alunos relacionem a mudança de sentido na reta numerada com o resultado das multiplicações.
Atividade Principal
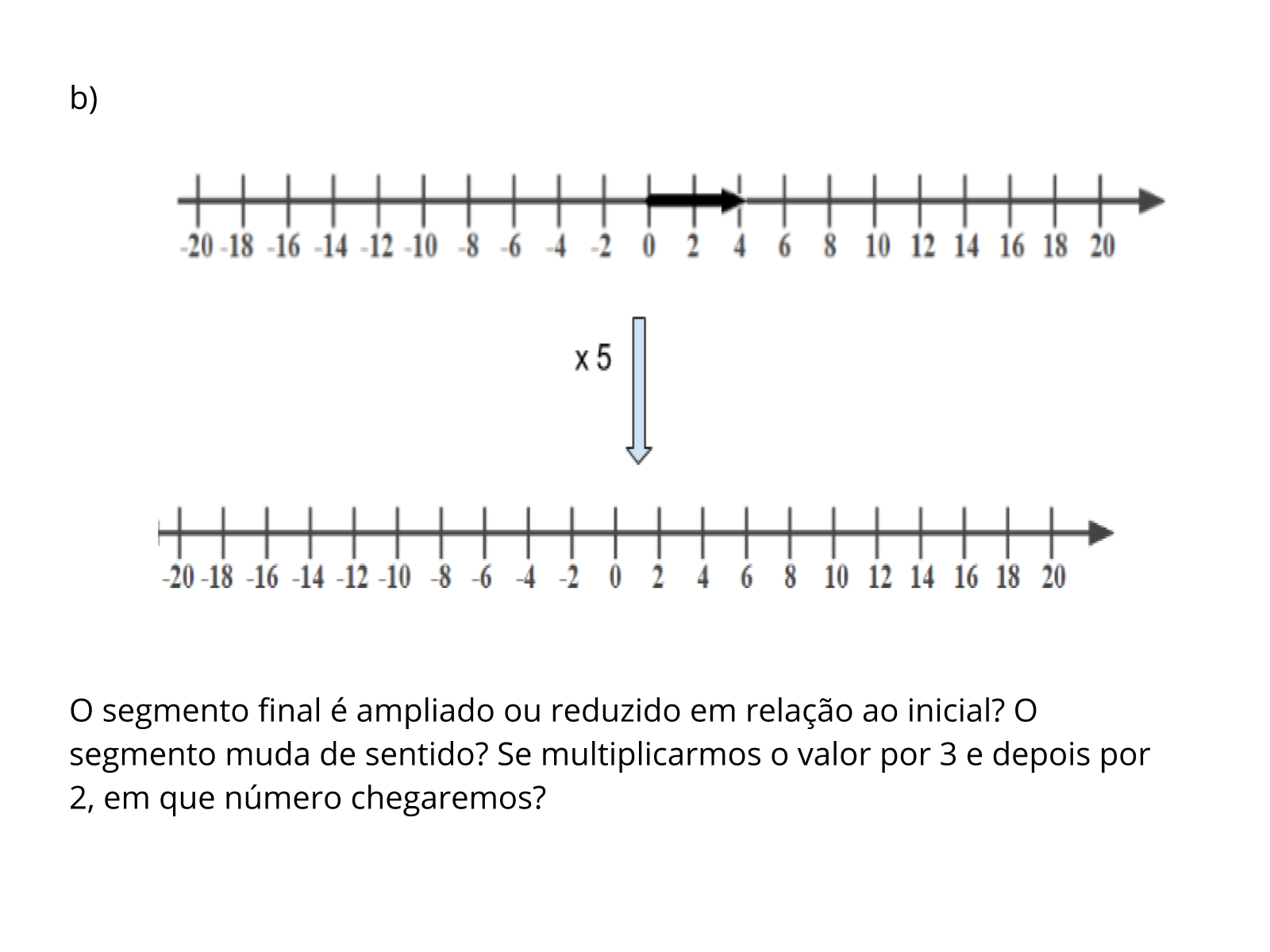
Tempo sugerido: 20 minutos (Slides 4 a 8)
Orientação:
- Você pode projetar, imprimir ou construir as retas numeradas na lousa. A utilização de papel quadriculado também pode auxiliar para a construção das retas.
- Organize os alunos em duplas ou trios e solicite que leiam os enunciados com muita atenção. Caminhe pela sala e veja se estão conseguindo representar adequadamente os segmentos na reta numerada com o sentido correto. Assim, poderá relacionar a mudança de sentido com a mudança de sinal quando a multiplicação ocorre por um número negativo.
- Evite falas como: “Menos com menos dá mais”, “Mais com menos dá menos”, etc. Isso causa grande confusão com os alunos ao trabalharem com soma e subtração, após terem trabalhado multiplicação e divisão.
Propósito: Fazer com que os alunos relacionem a mudança de sentido na reta numerada com o resultado das multiplicações.
Atividade Principal
Tempo sugerido: 20 minutos (Slides 4 a 8)
Orientação:
- Você pode projetar, imprimir ou construir as retas numeradas na lousa. A utilização de papel quadriculado também pode auxiliar para a construção das retas.
- Organize os alunos em duplas ou trios e solicite que leiam os enunciados com muita atenção. Caminhe pela sala e veja se estão conseguindo representar adequadamente os segmentos na reta numerada com o sentido correto. Assim, poderá relacionar a mudança de sentido com a mudança de sinal quando a multiplicação ocorre por um número negativo.
- Evite falas como: “Menos com menos dá mais”, “Mais com menos dá menos”, etc. Isso causa grande confusão com os alunos ao trabalharem com soma e subtração, após terem trabalhado multiplicação e divisão.
Propósito: Fazer com que os alunos relacionem a mudança de sentido na reta numerada com o resultado das multiplicações.
Atividade Principal
Tempo sugerido: 20 minutos (Slides 4 a 8)
Orientação:
- Você pode projetar, imprimir ou construir as retas numeradas na lousa. A utilização de papel quadriculado também pode auxiliar para a construção das retas.
- Organize os alunos em duplas ou trios e solicite que leiam os enunciados com muita atenção. Caminhe pela sala e veja se estão conseguindo representar adequadamente os segmentos na reta numerada com o sentido correto. Assim, poderá relacionar a mudança de sentido com a mudança de sinal quando a multiplicação ocorre por um número negativo.
- Evite falas como: “Menos com menos dá mais”, “Mais com menos dá menos”, etc. Isso causa grande confusão com os alunos ao trabalharem com soma e subtração, após terem trabalhado multiplicação e divisão.
Propósito: Fazer com que os alunos relacionem a mudança de sentido na reta numerada com o resultado das multiplicações.
Discussão das soluções
Tempo sugerido: 10 minutos (Slides 9 a 12)
Orientação:
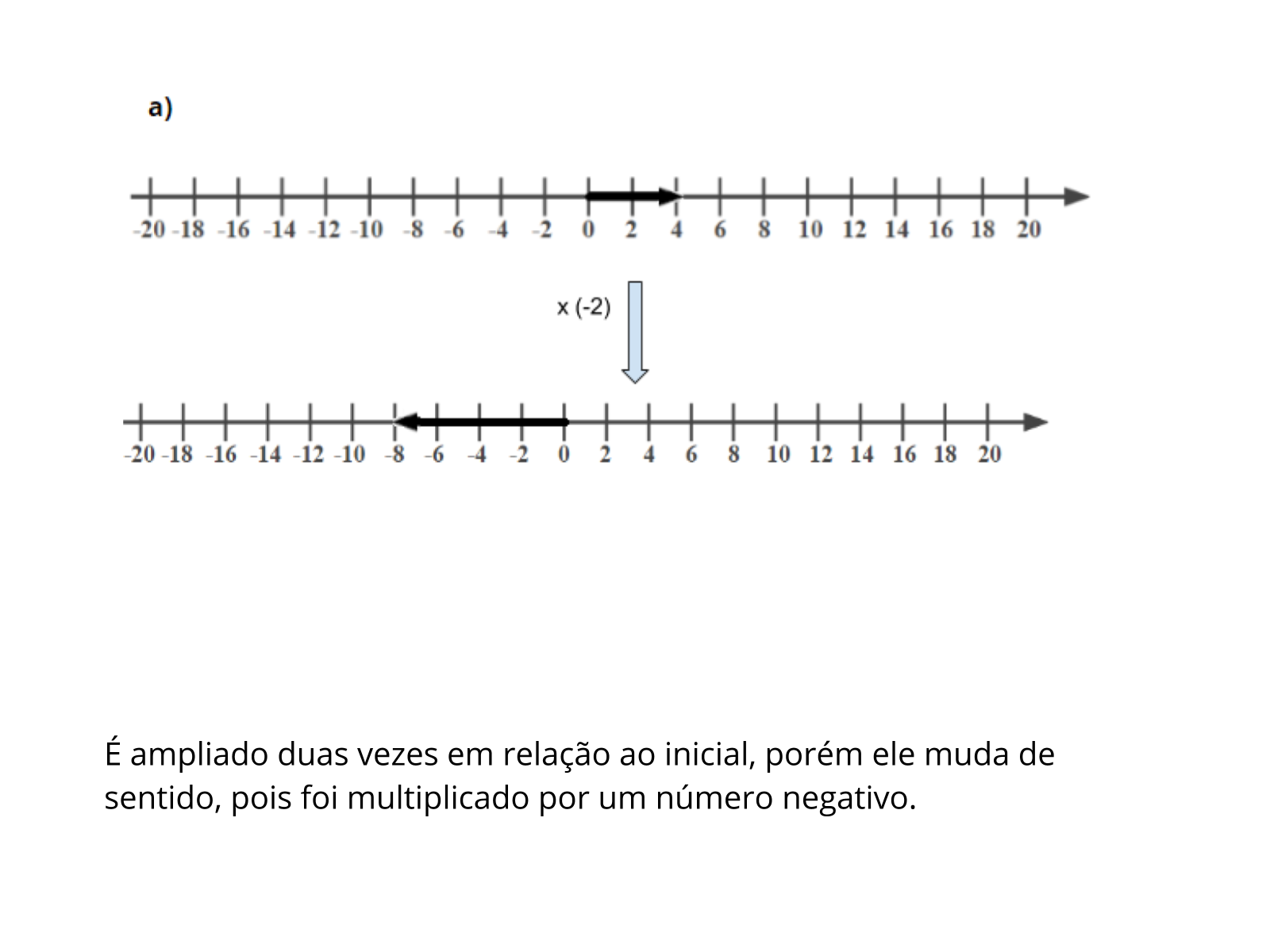
Comente com os alunos cada item e solicite para que apresentem suas respostas. A representação na reta numerada auxiliará na percepção da mudança de sentido e para perceber quantas vezes cada segmento foi ampliado. As setas podem auxiliar para a verificação dos sentidos.
Discuta com a turma:
- Qual é a origem de cada segmento? (o zero)
- Para ele ser reduzido, o número teria que ser multiplicado por quanto? (um número entre -1 e 1)
- O que a mudança de sentido nos revela?
Propósito: Perceber se os alunos conseguiram representar os segmentos nas retas e perceber a mudança de sentido em alguns casos.
Discussão das soluções
Tempo sugerido: 10 minutos (Slides 9 a 12)
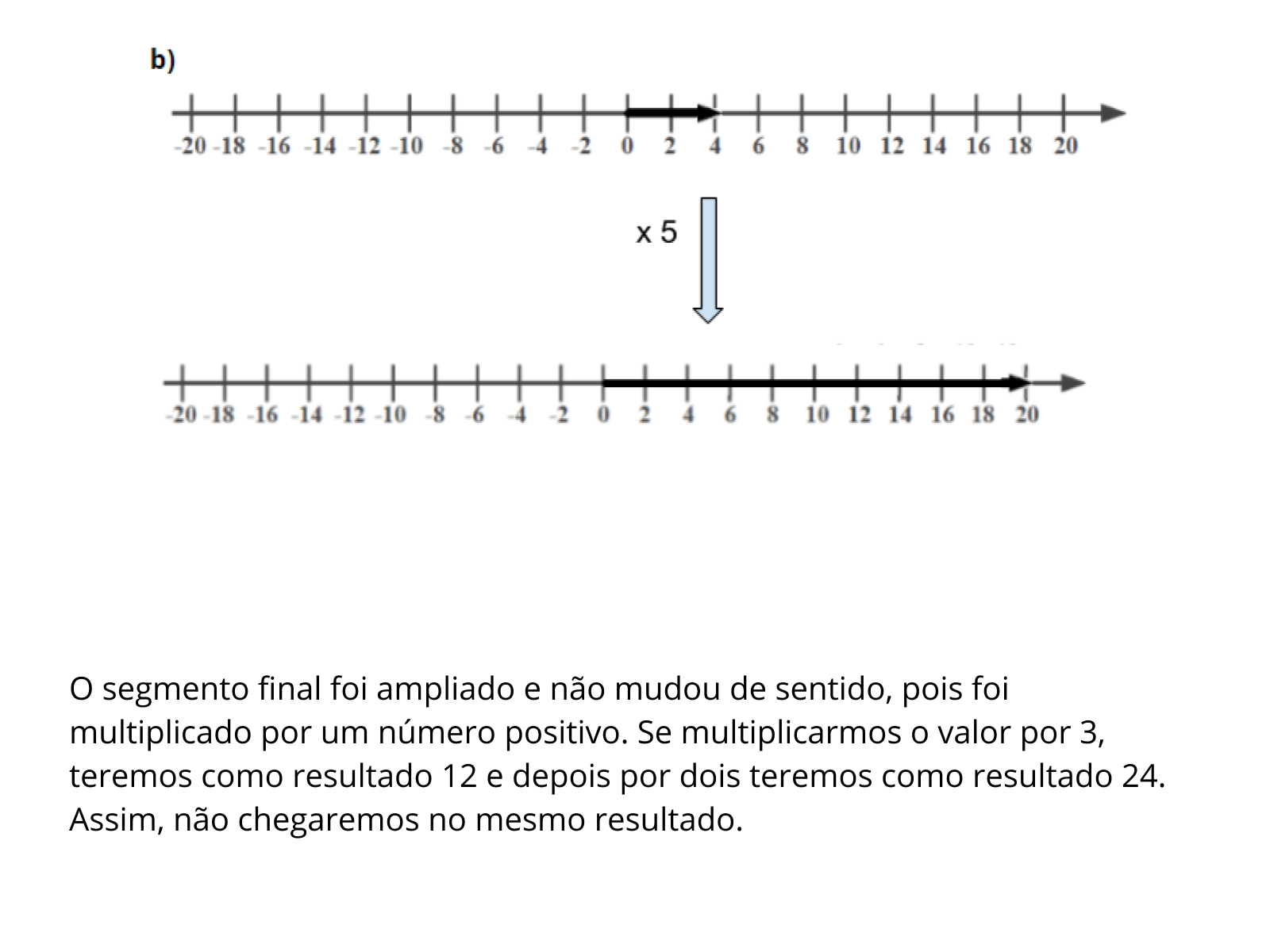
Orientação: Comente com os alunos cada item e solicite para que apresentem suas respostas. A representação na reta numerada auxiliará na percepção da mudança de sentido e para perceber quantas vezes cada segmento foi ampliado. As setas podem auxiliar para a verificação dos sentidos. Nesse caso, ao ser multiplicado por 5, o segmento apenas aumenta e seu sentido permanece o mesmo.
Propósito: Perceber se os alunos conseguiram representar os segmentos nas retas e perceber a mudança de sentido em alguns casos.
Discussão das soluções
Tempo sugerido: 10 minutos (Slides 9 a 12)
Orientação:
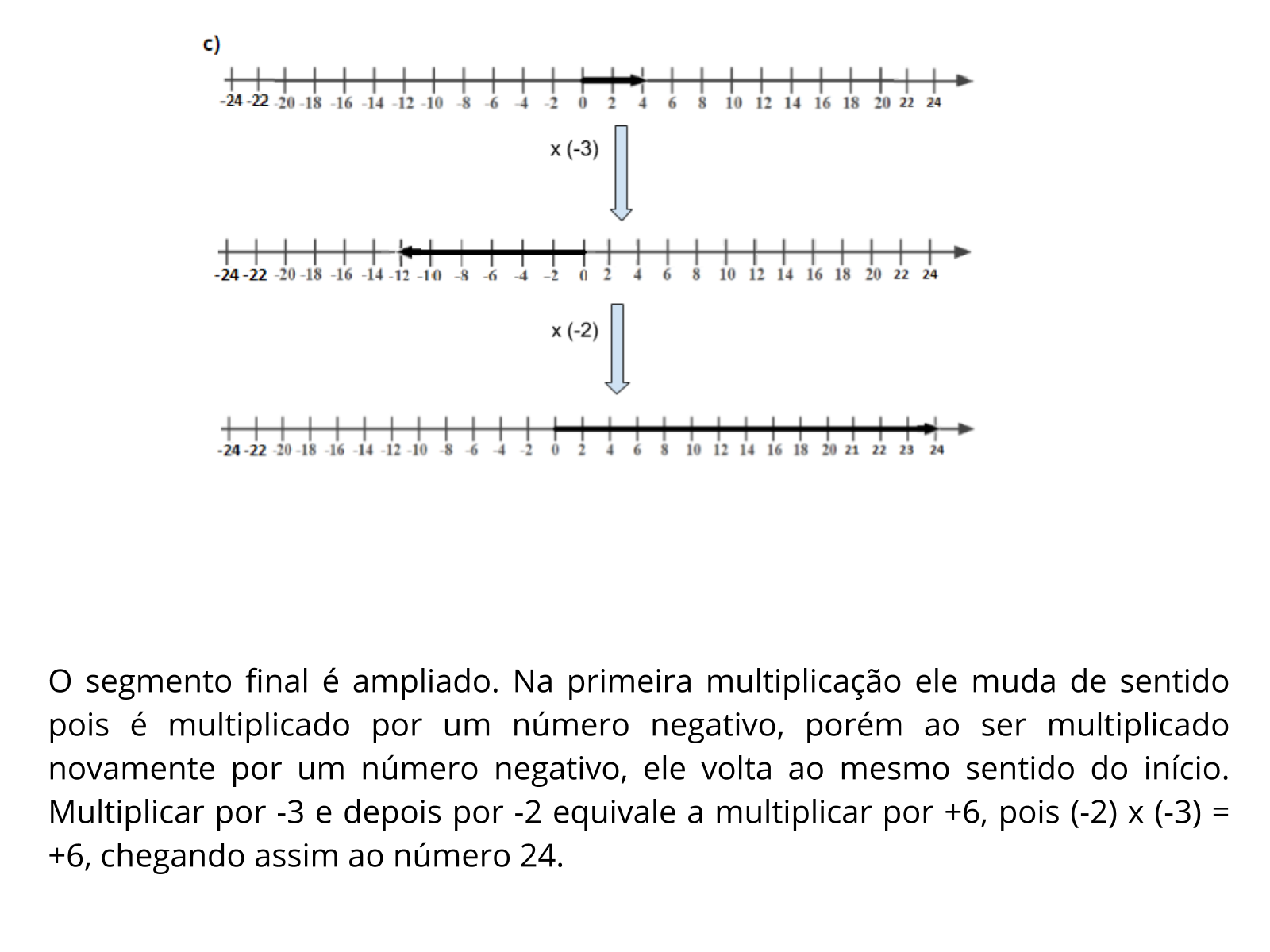
- Comente com os alunos cada item e solicite para que apresentem suas respostas. A representação na reta numerada auxiliará na percepção da mudança de sentido e para perceber quantas vezes cada segmento foi ampliado. As setas podem auxiliar para a verificação dos sentidos.
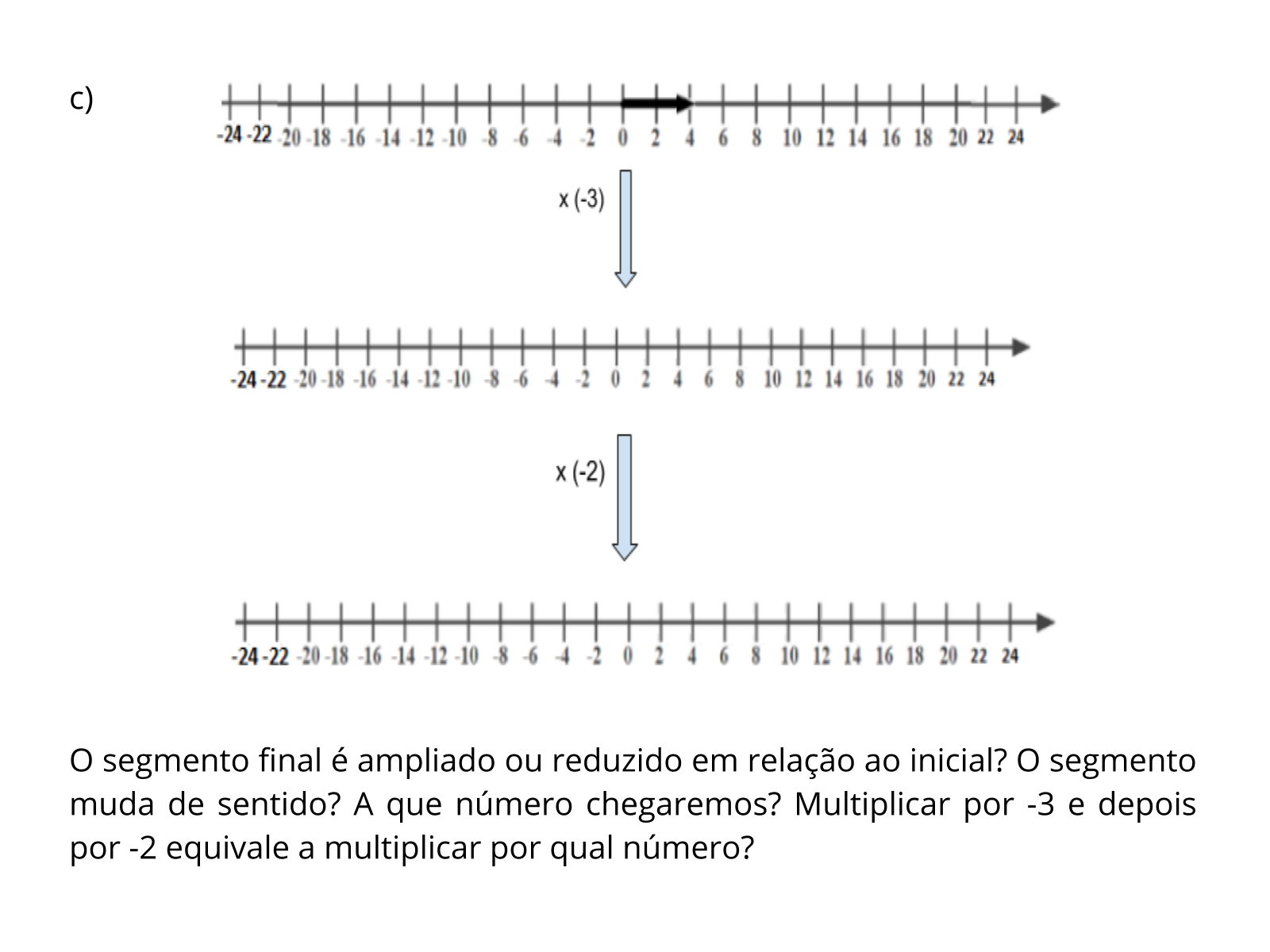
- Ao multiplicar por -3 e em seguida por -2, ocorre a mudança de sentido dua vezes. Assim, os alunos podem relacionar o sinal de menos com a alteração do sinal do produto.
Propósito: Perceber se os alunos conseguiram representar os segmentos nas retas e perceber a mudança de sentido em alguns casos.
Discussão das soluções

Tempo sugerido: 10 minutos (Slides 9 a 12)
Orientação:
- Comente com os alunos cada item e solicite para que apresentem suas respostas. A representação na reta numerada auxiliará na percepção da mudança de sentido e para perceber quantas vezes cada segmento foi ampliado. As setas podem auxiliar para a verificação dos sentidos.
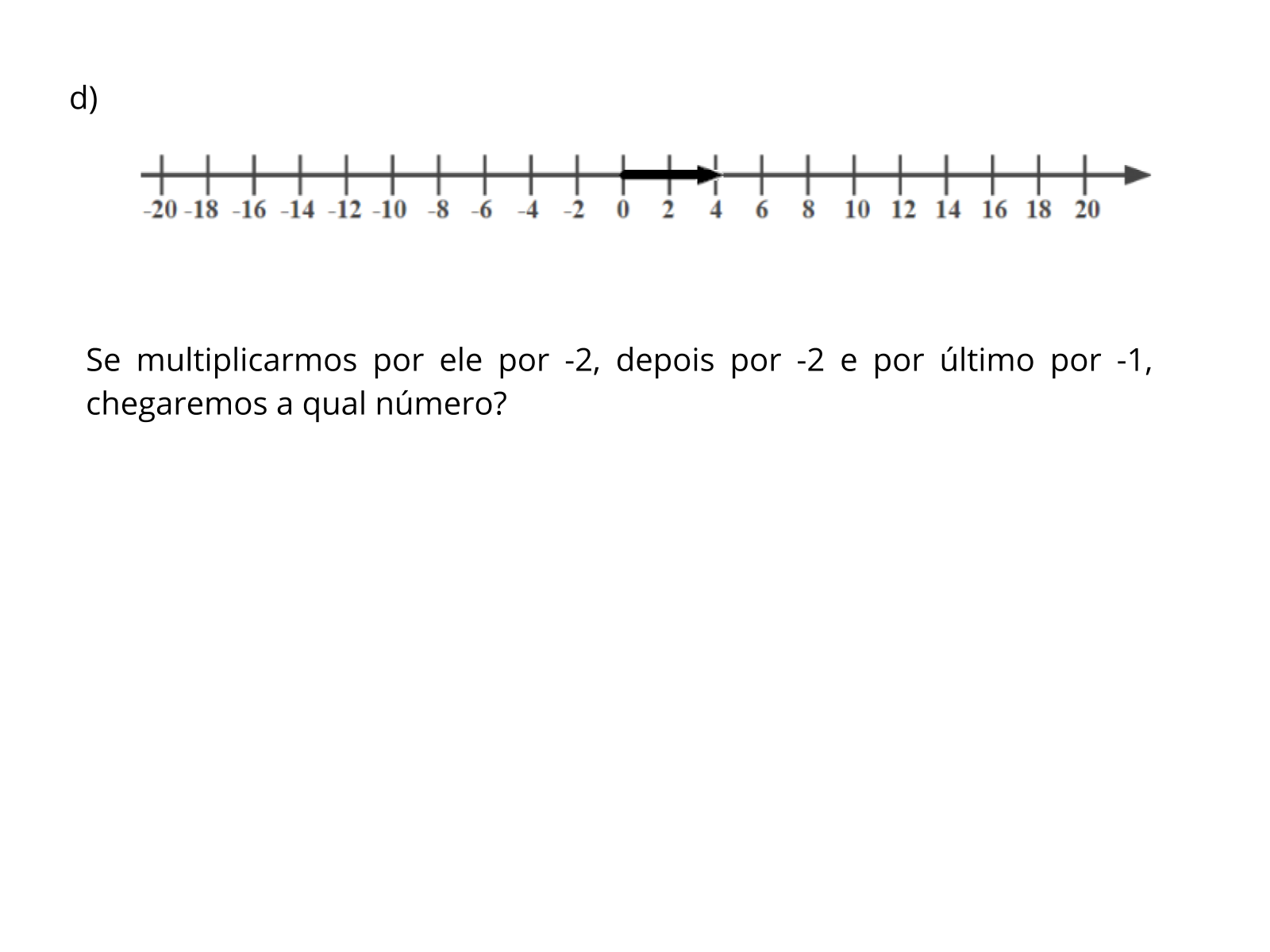
- Os alunos podem responder essa questão utilizando uma expressão numérica ou cada multiplicação separada uma da outra:
4 x (-2) x (-2) x (-1) =
-8 x (-2) x (-1) =
+16 x (-1) = -16
ou
4 x (-2) = -8
-8 x (-2) = +16
16 x (-1) = -16
Propósito: Perceber se os alunos conseguiram representar os segmentos nas retas e perceber a mudança de sentido em alguns casos.
Encerramento

Tempo sugerido: 2 minutos
Orientação: Comente sobre a atividade realizada, discuta sobre as representações na reta numerada e sobre os resultados das multiplicações envolvendo números inteiros.
Propósito: Finalizar a aula com comentários dos alunos sobre o que compreenderam da atividade.
Raio X

Tempo sugerido: 10 minutos (slides 14 a 16)
Orientação: Essa atividade será realizada individualmente. No 1º exercício, os alunos deverão descobrir os números que devem ser colocados em cada quadrado para que as sentenças sejam verdadeiras. Podem utilizar diferentes estratégias, por tentativa e erro ou pela operação inversa. No 2º exercício, eles deverão trabalhar com a ideia de multiplicar um segmento de reta orientado para descobrir as operações efetuadas.
Materiais complementares:
Raio X
Tempo sugerido: 10 minutos (slides 14 a 16)
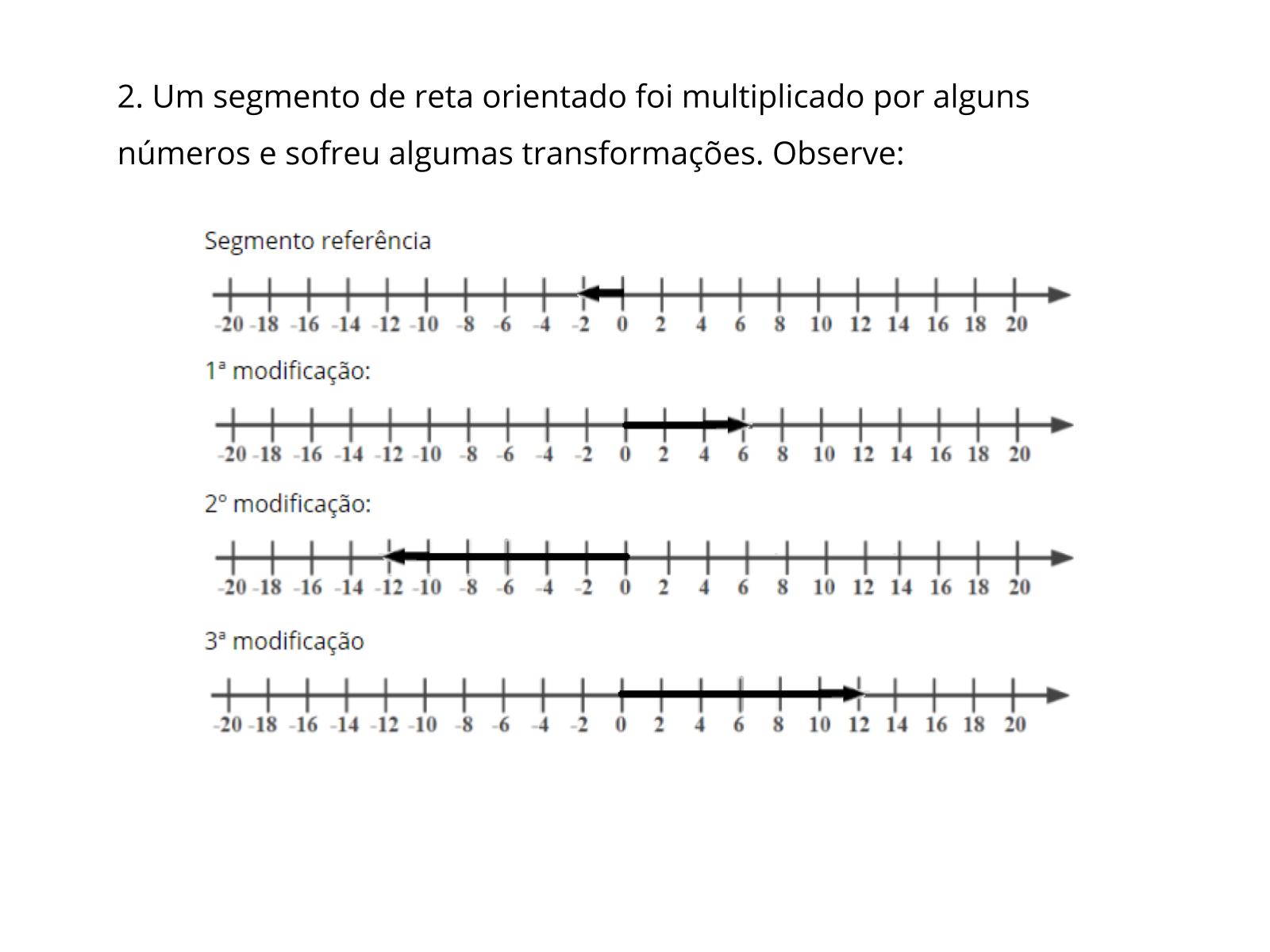
Orientação: Essa atividade será realizada individualmente. No 1º exercício, os alunos deverão descobrir os números que devem ser colocados em cada quadrado para que as sentenças sejam verdadeiras. Podem utilizar diferentes estratégias, por tentativa e erro ou pela operação inversa. No 2º exercício, eles deverão trabalhar com a ideia de multiplicar um segmento de reta orientado para descobrir as operações efetuadas.
Raio X

Tempo sugerido: 10 minutos (slides 14 a 16)
Orientação: Essa atividade será realizada individualmente. No 1º exercício, os alunos deverão descobrir os números que devem ser colocados em cada quadrado para que as sentenças sejam verdadeiras. Podem utilizar diferentes estratégias, por tentativa e erro ou pela operação inversa. No 2º exercício, eles deverão trabalhar com a ideia de multiplicar um segmento de reta orientado para descobrir as operações efetuadas.
Para os alunos
Para o professor
Sugestão de adaptação para ensino remoto
Recursos
Necessários:
- Caderno;
- Lápis;
- Régua;
- Grupo de alunos no Whatsapp;
- Zoom;
- Tabuleiro e peças do jogo.
Opcionais:
- Google Sala de Aula;
- Meet;
- Podcast.
Para este plano, foque na etapa Atividade Principal.
Aquecimento
A atividade é uma retomada de conceitos que são fundamentais para a aula. Organize um encontro usando o Meet, Zoom ou grave um vídeo para a conversar com os alunos sobre a multiplicação de números inteiros. Use uma apresentação em Powerpoint para exemplificar uma resolução de expressão numérica. Estimule a conversa com boas perguntas, como:
- Os parênteses são importantes?
- Se eu colocasse mais um número, por exemplo: (-4) x (+5) x (-2), qual seria o sinal do resultado?
Ouça com atenção as respostas e anote-as para recuperá-las durante a discussão da atividade principal.
Atividade principal
Para a realização da atividade principal, os alunos precisam ter acesso à tabela para responder a proposta. Para isso, fotografe e compartilhe a atividade no grupo de Whatsapp ou Google Classroom, para que os alunos possam pensar e compartilhar estratégias para encontrar os valores desconhecidos.
Incentive-os a relacionar a mudança de sentido na reta numerada com o resultado das multiplicações. Oriente-os a filmar ou fotografar as estratégias e respostas, para compartilhar com o professor e a turma no momento da discussão das soluções.
Discussão das soluções
A discussão das soluções da atividade é uma etapa importantíssima da aula. É o momento de justificar as estratégias e respostas usadas para a resolução do problema proposto na atividade principal. Os alunos devem postar os vídeos ou fotografias para compartilhar as respostas em um ambiente de interação, como Whatsapp ou Google Sala de Aula.
Ouça os comentários dos alunos sobre as regularidades percebidas. Comente sobre a atividade realizada, discuta sobre as representações na reta numerada e os resultados das multiplicações envolvendo números inteiros.
Raio X
O raio x é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto. Compartilhe a imagem do slide com os alunos usando o recurso de e-mail.
Peça para responderem a questão e devolva o e-mail com ela resolvida. Analise as respostas e elabore devolutivas individuais sobre a atividade e reenvie com comentários para os alunos.
Convite às famílias
A participação das famílias no processo de aprendizagem é de grande importância para o aluno. Porém, ressaltamos que os pais não são professores de matemática e muitos estão ocupados com outras funções em casa. Portanto, indicamos a participação das famílias no compartilhamento e discussão de possíveis soluções para os problemas propostos.
Este plano de aula foi elaborado pelo Time de Autores NOVA ESCOLA
Autor: Danilo Pires de Azevedo
Mentor: Ferdinando Caíque Genghini Dantas Lobo
Especialista de área: Luciana Maria Tenuta de Freitas
Habilidade da BNCC
(EF07MA04) Resolver e elaborar problemas que envolvam operações com números inteiros.
Objetivos específicos
- Representar na reta numerada segmentos de reta quando multiplicados por um número negativo ou positivo.
- Resolver situações-problema envolvendo números inteiros.
- Utilizar a operação básica de multiplicação envolvendo números inteiros de forma adequada.
Conceito-chave
Multiplicação de números inteiros; modificações na reta numerada a partir de multiplicações; sentido e relação com números inteiros.
Recursos necessários
Lápis, borracha e régua. Se possível, papel quadriculado.
















