Resumo da aula
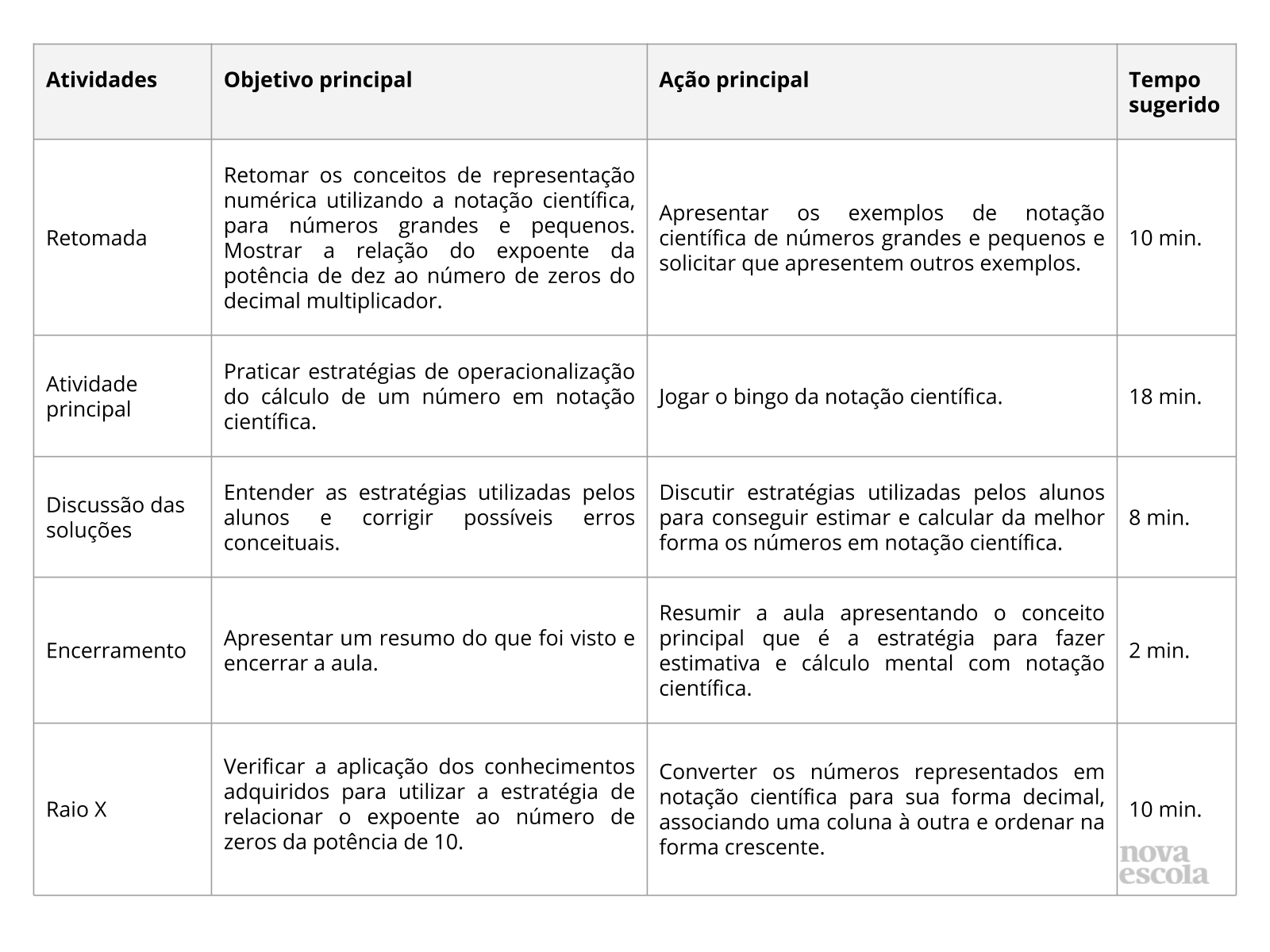
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo

Tempo sugerido: 2 minutos
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada

Tempo sugerido: 10 minutos. (Slides 3, 4, 5 e 6)
Orientação: Relembre com os alunos alguns conceitos da notação científica. Procure fazer perguntas e deixar com que eles expliquem com suas palavras o que já foi aprendido sobre o assunto.
Propósito: Retomar com os alunos como os números são representados em notação científica, dando especial ênfase à relação do expoente da potência de dez à quantidade de zeros do número decimal formado.
Discuta com a turma:
- Para que serve a notação científica? Resp.: Muitas e elaboradas podem ser as respostas, uma comumente aceita é para encurtar a representação de números muito grandes ou pequenos, com muitos zeros.
- O que é a mantissa? Resp.: Explicado já algumas vezes, mas é bom perguntar a eles e deixe que se expressem. A mantissa é o valor que multiplica a potência de dez, e como é falado na aula, o algarismo mais significativo da mantissa deve estar entre 1 e 9.
- Por que a potência de dez é usada e não outra potência? Resp.: Nosso sistema de numeração é o decimal. Em se tratando de computadores, a base utilizada na potência é o 2.
Retomada

Tempo sugerido: 10 minutos. (Slides 3, 4, 5 e 6)
Orientação: Apresente os exemplos para os alunos ressaltando o expoente e o número de zeros do multiplicador decimal.
Propósito: Mostrar a relação entre o expoente da potência de dez e o número de zeros no correspondente número decimal. Para este caso, expoentes positivos.
Discuta com a turma:
- Peça para os alunos citarem um número inteiro multiplicado por uma potência de 10 com expoente positivo, que seja diferente dos exemplos mostrados.
- Qual a diferença de um número inteiro multiplicado pela potência de dez e um número decimal não inteiro? Resp.: Se reparar o resultado da multiplicação do número inteiro, terá a mesma quantidade de zeros indicados na potência de dez. Já o número decimal, terá os zeros substituídos pelos décimos, centésimos, milésimos, etc.
Retomada

Tempo sugerido: 10 minutos. (Slides 3, 4, 5 e 6)
Orientação: Relembre com os alunos alguns conceitos da notação científica, procure fazer perguntas e deixar com que eles expliquem com suas palavras o que já foi aprendido sobre o assunto.
Propósito: Retomar com os alunos como os números são representados em notação científica, dando especial ênfase à relação do expoente da potência de dez à quantidade de zeros do número decimal formado.
Retomada

Tempo sugerido: 10 minutos. (Slides 3, 4, 5 e 6)
Orientação: Apresente os exemplos para os alunos ressaltando o expoente e o número de zeros do multiplicador decimal. Não é necessário comentar essa formalidade com os alunos, mas é importante que o professor veja que se o expoente for -N, haverá N zeros (contando o zero à esquerda da vírgula) até o algarismo significativo da mantissa, ou então, há N-1 zeros entre a vírgula e o algarismo significativo da mantissa. Faça os alunos perceberem isso através de exemplos numéricos.
Propósito: Mostrar a relação entre o expoente da potência de dez e o número de zeros no correspondente número decimal. Para este caso, expoentes negativos.
Discuta com a turma:
- Peça para os alunos citarem um exemplo de um número inteiro multiplicado por uma potência de 10 com expoente negativo, que seja diferente dos exemplos mostrados.
- Se o expoente é -3, quantos zeros temos antes do algarismo significativo da mantissa? Resp.: 3 = 0,000...
- Se o expoente é -3, quantos zeros temos depois (à direita) da vírgula até o algarismo significativo da mantissa? Resp.: 2 = 0,00...
- Se o expoente é -5, quantos zeros temos antes do algarismo significativo da mantissa? Resp.: 5 = 0,0000...
- Se o expoente é -5, quantos zeros temos depois (à direita) da vírgula até o algarismo significativo da mantissa? Resp.: 4 = 0,0000...
Atividade Principal

Tempo sugerido: 18 minutos
Orientação: Cada cartela é composta por 9 números escritos na forma decimal.
O professor sorteia um número e “canta” em notação científica, pode também anotar no quadro, até mesmo para conferir depois. O aluno deve conseguir interpretar mentalmente ou com um rascunho do lado para marcar o número correspondente na cartela.
O aluno que completar o jogo (em uma das formas escolhidas abaixo) deve gritar “BINGO” e então o professor confere se os números marcados estão de acordo com os que foram falados.
Jogo 1: Completar uma linha, uma coluna ou uma diagonal. (3 números)
Jogo 2: Duas diagonais ou um X (5 números)
Jogo 3: Uma cartela por aluno (Deve completar a cartela = 9 números)
Jogo 4: Duas cartelas por aluno (Deve completar as duas cartelas = 18 números)
Importante!
Lembre-se de levar algo para os alunos marcarem as cartelas, milho, feijão, pedacinhos de papel. Mais de 9 por aluno por cartela ou mais de 18 para duas cartelas, pois eles sempre acabam perdendo alguns. Se eles marcarem com lápis ou caneta, as cartelas serão descartáveis e essa não é a intenção do jogo, pois a ideia é recolhê-las ao final da atividade para poderem ser utilizadas por outros alunos.
Propósito: Que o aluno seja capaz de mentalmente fazer estimativas e cálculos para representar números usando a notação científica.
Materiais complementares para impressão:
Atividade principal
Resolução da atividade principal
Guia de Intervenções
Discussão da Solução

Tempo sugerido: 8 minutos
Orientação: Após o jogo, conversar com a turma sobre as dificuldades e estratégias utilizadas para a encontrar os números e se com o tempo eles criaram algum método que foi seguido para encontrar a solução mais facilmente.
Propósito: Entender as estratégias utilizadas pelos alunos e corrigir possíveis erros conceituais.
Discuta com a turma:
- Quais estratégias vocês usaram para fazer essas conversões? Alguma diferente daquelas que estudamos?
Encerramento

Tempo sugerido: 2 minutos
Orientação: Encerre a atividade apresentando o resumo da aula. O conceito principal é a estratégia para fazer estimativa e cálculo mental com notação científica.
Raio X

Tempo sugerido: 10 minutos
Orientação: Peça que, individualmente, os alunos leiam a atividade e a realizem. Circule para verificar como os alunos estão resolvendo, verifique se há dificuldade na ordenação crescente dos números. Para esta atividade é possível avaliar se os alunos entenderam a estratégia da relação do expoente à quantidade de zeros bem como avaliar se eles têm noção da ordem de grandeza, quais números são maiores que os outros.
Propósito: Avaliar o efeito dos jogos e da aula mais lúdica na consolidação do aprendizado individual.
Discuta com a turma:
- Como saber quando um número é maior que o outro? Resp: Se os números estiverem em notação científica, olhar os expoentes já dará uma boa ideia da ordem de grandeza de um número, depois basta olhar o algarismo mais significativo da mantissa, o que está à esquerda da vírgula.
- Como saber se um número é maior do que o outro se os expoentes são iguais? Resp.: Se os expoentes são iguais, usa-se a estratégia normal de avaliar se um número é maior que outro, como o número está em notação científica, avalia a unidade, décimo, centésimo, milésimo e assim por diante.
Materiais complementares para impressão:
Atividade Raio X
Resolução do Raio X
Atividade complementar
Resoluções da atividade complementar





















