Resumo da aula
Resumo da aula
Orientações:Este slide não é um substituto para as anotações para o professor e não deve ser apresentado para os alunos. Trata-se apenas de um resumo da proposta para apoiá-lo na aplicação do plano em sala de aula.
Orientação: Leia atentamente o plano inteiro e as anotações para o professor. Busque antecipar quais questões podem surgir com a sua turma e preveja adequações ao nível em que seus alunos estão.
Compartilhe o objetivo da aula com os alunos antes de aplicar proposta.
Na aba “Sobre o plano”, confira os conhecimentos que sua turma já deve dominar para seguir essa proposta.
Se quiser salvar o plano no seu computador, faça download dos slides na aba “Materiais complementares”. Você também pode imprimi-lo clicando no botão “imprimir”.
Objetivo
Objetivo
Tempo sugerido: 2 minutos.
Orientação: Projete ou leia o objetivo para a turma.
Propósito: Compartilhar o objetivo da aula.
Retomada
Retomada
Tempo sugerido: 9 minutos
Orientação: Projete o slide ou leia o texto para os alunos. Não use muito tempo para esse slide. As informações ficarão mais claras para os estudantes nos próximos slides.
Propósito: Contextualizar a aula.
Material complementar para o professor:
Retomada
Retomada
Tempo sugerido: 9 minutos
Orientação: Projete ou escreva a pergunta e a imagem na lousa. Explique para os alunos o que essas cartas representam: Em uma família com 5 monstros, cada um tem 4 pernas e 7 olhos. Quantas pernas e quantos olhos há no total nessa família? Em grupos de três ou quatro alunos, peça para que eles discutam por um minuto. Abra a discussão para toda a turma e, à medida em que os alunos compartilharem suas ideias, faça a sistematização no quadro, de forma que todas as contribuições fiquem visíveis e organizadas de acordo com a pergunta a que se referem.
Propósito: Relembrar a construção dos fatos fundamentais da multiplicação.
Discuta com a turma:
- Quais as estratégias usadas?
- Há mais de uma “boa” estratégia para a resolução de um mesmo cálculo?
- Há outros significados e formas de se resolver essas operações?
Solução:
Número total de pernas = número de monstros x número de pernas em cada monstro = 5 x 4 = 20
Possíveis estratégias (caso o fato fundamental ainda não seja fluente):
5 x 4 = 4 + 4 + 4 + 4 + 4 = 20
5 x 4 = 4 x 5 = 5 + 5 + 5 + 5 = 20
5 x 4 = 5 x 2 x 2 = 10 x 2 = 20
Número total de olhos= número de monstros x número de olhos em cada monstro = 5 x 7 = 35
Possíveis estratégias (caso o fato fundamental ainda não seja fluente):
5 x 7 = 7 + 7 + 7 + 7 + 7 = 35
5 x 7 = 7 x 5 =5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
5 x 7 = 5 x 4 + 5 x 3 = 20 + 15 = 35
Material complementar para o professor
- Leia o capítulo 11 (Ajudando as Crianças a Dominar os Fatos Fundamentais) de VAN DE WALLE, John A. Matemática no Ensino fundamental: formação de professores e aplicação em sala de aula. Porto Alegre: Artmed, 2009.
- Leia a matéria Um novo jeito de ensinar a tabuada. Disponível em https://novaescola.org.br/conteudo/162/novo-jeito-ensinar-tabuada. Acesso em 15/01/2018.
Retomada
Retomada
Tempo sugerido: 9 minutos
Orientação: Projete ou escreva a pergunta e a imagem na lousa. Explique para os alunos o que essas cartas representam: Em uma família com 5 monstros, há no total 20 pernas e 35 olhos. Quantas pernas e quantos olhos há em cada membro dessa família? Em grupos de três ou quatro alunos, peça para que eles discutam por um minuto. Abra a discussão para toda a turma e, à medida em que os alunos compartilharem suas ideias, faça a sistematização no quadro, de forma que todas as contribuições fiquem visíveis e organizadas de acordo com a pergunta a que se referem. Peça que os alunos façam conexões com o que está sistematizado da discussão anterior. Uma vez que a família de monstros é a mesma, os números serão os mesmos e essas conexões serão fáceis.
Propósito: Relembrar a construção dos fatos fundamentais da divisão. Relembrar a relação entre multiplicação e divisão.
Discuta com a turma:
- Quais as estratégias usadas?
- Há mais de uma “boa” estratégia para a resolução de um mesmo cálculo?
- Qual a relação entre a multiplicação e a divisão?
- Há outros significados e formas de se resolver essas operações?
Solução:
Número de pernas de cada monstro = número total de pernas : número de monstros = 20 : 5 = 4
Possíveis estratégias (caso o fato fundamental ainda não seja fluente):
20 = 5 + 5 + 5 + 5 (4x) ? 20 : 5 = 4
5 x 4 = 20 ? 20 : 5 = 4
Número de olhos de cada monstro = número total de olhos : número de monstros = 35 : 5 = 7
Possíveis estratégias (caso o fato fundamental ainda não seja fluente):
35 = 5 + 5 + 5 + 5 + 5 + 5 + 5 (7x)? 35 : 5 = 7
5 x 7 = 35 ? 35 : 5 = 7
Atividade principal
Atividade principal
Tempo sugerido: 25 minutos
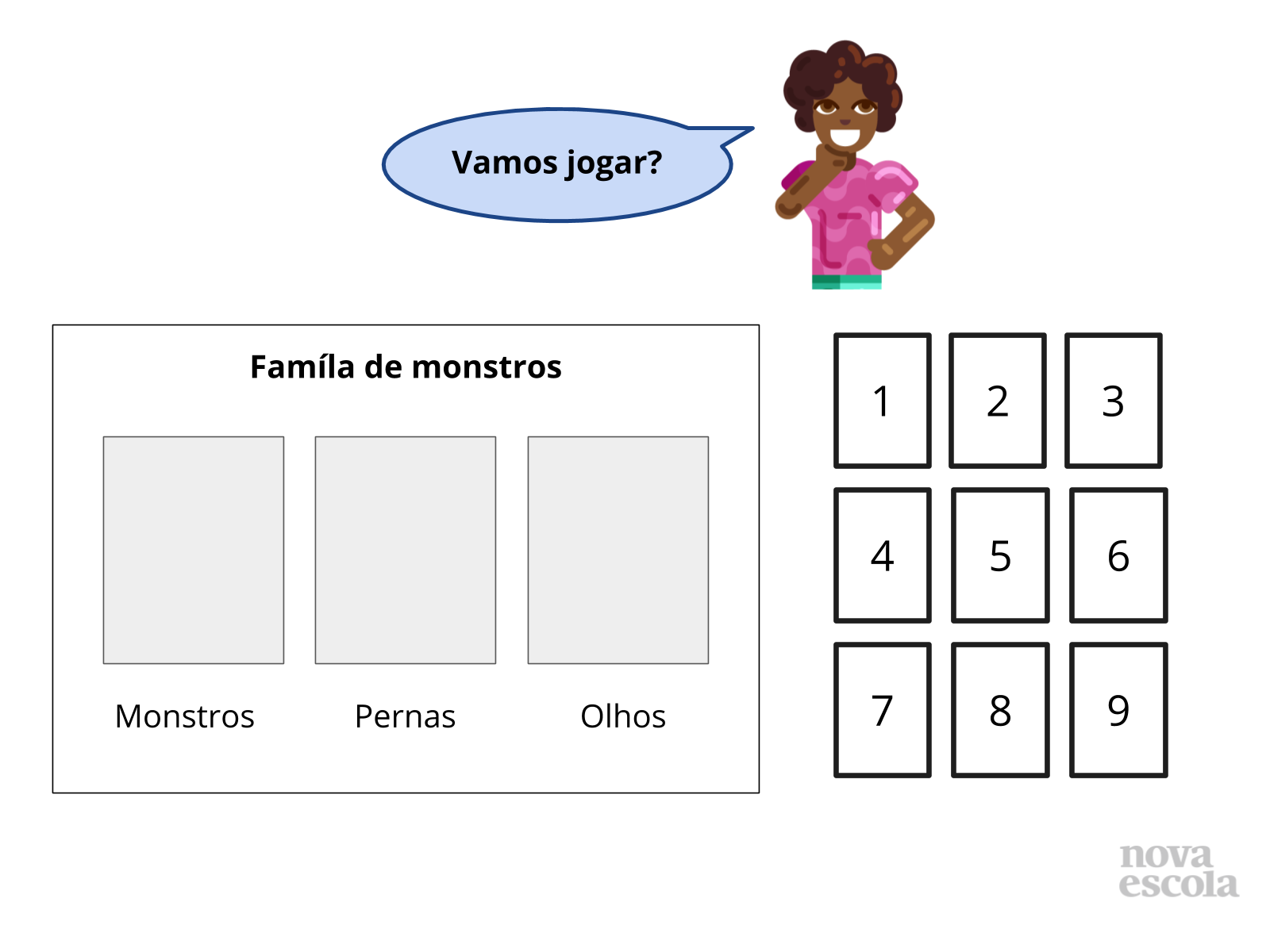
Orientação: Proponha aos alunos o jogo “Famílias de Monstros”, para a prática dos fatos fundamentais da multiplicação e divisão. Se possível, imprima as regras e entregue para os estudantes. Leia as regras com os alunos para tirar eventuais dúvidas. Caso não consiga imprimir uma cópia para cada aluno ou uma por dupla, registre no quadro ou em um cartaz onde todos consigam ler. Após a leitura das regras, também é possível pedir a um aluno que, voluntariamente, explique para a classe como se joga. Pergunte se alguém gostaria de propor alguma outra regra ou modificar alguma das listadas. No caso de propostas serem feitas, discuta rapidamente o motivo da modificação e consulte a turma antes de mudar. Os alunos devem anotar as modificações nas folhas impressas ou em suas anotações.
Escolha alguns alunos para fazerem uma rodada demonstrativa na lousa. Caso ainda tenha alguma dúvida, este é um bom momento para esclarecê-las. Eles podem ainda anotar as regras no caderno para poder jogar em outras ocasiões com amigos ou com a família.
Organize os alunos em duplas ou grupos de 3 alunos. Cada grupo precisará de uma ficha por integrante, 9 cartas numeradas de 1 a 9 e papel para anotações. Você pode imprimir as fichas e cartas aqui ou os alunos poderão fazer suas próprias fichas e cartas conforme o modelo desse slide. As cartas com números devem ser do mesmo tamanho e recortadas e coladas em um papel mais grosso, para que o número não possa ser visto do verso. Proponha aos alunos que joguem algumas rodadas sozinhos. Neste momento, circule entre os alunos, observando como eles jogam, calculam e registram seus resultados. Preste atenção especial a como os alunos, quando chegam a resultados diferentes, explicam suas estratégias uns aos outros. Se não explicarem, intervenha, pedindo que expliquem até que todos do grupo compreendam qual a resposta correta e como chegar nela. Em caso de dúvidas, peça para que conversem com os colegas para tentar resolver. Faça anotações sobre o que observar nesse momento. Entre as rodadas, converse com os alunos sobre as questões listadas abaixo.
Propósito: Compreender as regras de um jogo e discuti-las. Desenvolver fluência nos fatos fundamentais da multiplicação e divisão.
Discuta com a turma:
- Por onde você está começando?
- Qual estratégia você escolheu nesse caso?
- Você já sabe automaticamente alguma dessas respostas?
- O que está sendo mais difícil?
- Como você está resolvendo suas dificuldades?
- Você já perguntou aos seus colegas sobre quais estratégias eles estão usando?
- Você já compartilhou essa estratégia com seus colegas? Como pode fazer isso?
Materiais complementares:
Atividade
Principal
Atividade
principal
Resolução da atividade
Guia de intervenção
Material complementar para o professor:
Discussão da solução
Discussão da solução
Tempo sugerido: 7 minutos
Orientação: Peça aos alunos que compartilhem estratégias e dificuldades que usaram e enfrentaram durante o jogo. Peça que 3 ou 4 alunos compartilhem como resolveram as dificuldades ou como um colega lhe explicou os possíveis equívocos. Pergunte se alguém usou diferentes estratégias dependendo dos números envolvidos. Peça que compartilhem. Nesse momento, retome as anotações que você fez durante a observação do jogo e convide alunos específicos a compartilharem suas estratégias e dificuldades, de acordo com o que foi observado. Dessa forma, haverá uma variedade a ser discutida. Anote os nomes dos alunos que compartilharam suas resoluções próximo ao registro da estratégia.
Converse também com os alunos sobre quais os fatos fundamentais nos quais eles já apresentam fluência, aqueles cujo resultado já é automático, e quais ainda necessitam maior raciocínio e tempo para se saber o resultado.
Propósito: Discutir estratégias e dificuldades encontradas durante o jogo.
Discuta com a turma:
- Quais estratégias você utilizou durante o jogo?
- A estratégia que você encontrou foi bem sucedida?
- O que você aprendeu com a sua estratégia?
- Em que situação cada estratégia foi mais utilizada?
- Quais as dificuldades que apareceram?
- Como as dificuldades foram resolvidas?
- Quais os fatos fundamentais que vocês já dominam?
- Quais ainda necessitam mais tempo para saber o resultado?
Encerramento
Encerramento
Tempo sugerido: 2 minutos
Orientações: Encerre a atividade retomando com os estudantes as atividades feitas nesta aula e o que foi aprendido. Retome com os alunos os fatos fundamentais já fluentes e aqueles mais complicados. Peça que compartilhem estratégias para lembrá-los. Anote as contribuições na lousa, de forma que fiquem visíveis para todos.
Propósito: Sistematizar a aprendizagem, revisando o que foi estudado.
Discuta com a turma:
- O que fizemos nessa aula?
- O que aprendemos ou praticamos nessa aula?
- Quais os fatos fundamentais já fluentes para vocês?
- Quais estratégias vocês usam para lembrar mais facilmente alguns resultados?
Raio X
Tempo sugerido: 5 minutos
Orientações: Para finalizar a aula, apresente o exercício para os alunos. Você poderá projetá-lo ou imprimi-lo. Peça aos alunos que leiam e façam o desenho individualmente. Circule para verificar como os alunos estão realizando os cálculos. O Raio X é um momento para você avaliar se todos os estudantes conseguiram avançar no conteúdo proposto, então procure identificar e anotar os comentários de cada um. No final, reserve um tempo para um debate coletivo registrando as soluções no quadro.
Propósito: Verificar o que os alunos aprenderam na aula.
Discuta com a turma:
- Sobre o que foi a nossa aula hoje?
- O que você aprendeu com ela?
- Existem diferentes formas de resolver esse problema?
- Qual seria a forma mais prática de resolver esse problema?
Material complementar para o professor:
Raio X para impressão
Resolução do Raio X
Atividade complementar
Resolução da Atividade complementar
Outros jogos de matemática podem ser encontrados
